Основы работы в MatLab

1. Основы работы в MatLab

2.

MATLAB (сокращение от англ. «Matrix
Laboratory») – пакет прикладных программ для
решения задач технических вычислений и
одноимённый язык программирования,
иcпользуемый в этом пакете.

3. История создания

MATLAB как язык программирования был разработан Кливом
Моулером (англ. Cleve Moler) в конце 1970-х годов, в
университете Нью-Мексико.
Целью разработки служила задача дать студентам факультета
возможность использования программных библиотек Linpack и
EISPACK без необходимости изучения Фортрана.
Кливом Моулером, Джон Литтл и Стивом Бангертом
переписали MATLAB на C и основали в 1984 компанию The
MathWorks для дальнейшего развития.
Первоначально MATLAB предназначался для проектирования
систем управления (основная специальность Джона Литтла), но
быстро завоевал популярность во многих других научных и
инженерных областях.

4. Применение MatLab

MATLAB предоставляет пользователю большое
количество (несколько сотен) функций для анализа
данных, покрывающие практически все области
математики, в частности:
Матрицы и линейная алгебра
Многочлены и интерполяция
Математическая статистика и анализ данных
Обработка данных
Дифференциальные уравнения
Разреженные матрицы
Целочисленная арифметика
5

5. Разработка алгоритмов

MATLAB предоставляет удобные средства для
разработки алгоритмов, включая высокоуровневые с
использованием концепций объектно-ориентированного
программирования. В нём имеются все необходимые
средства интегрированной среды разработки.
Функции для работы с целыми типами данных облегчают
создание алгоритмов для микроконтроллеров и других
приложений, где это необходимо.
6

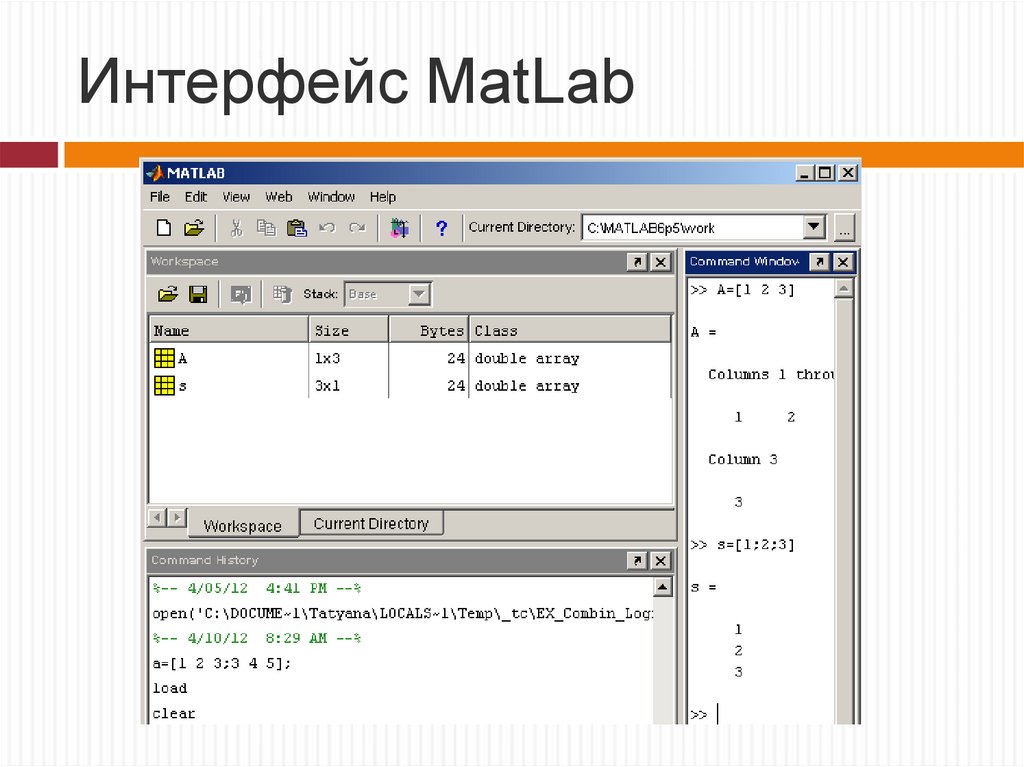
6. Интерфейс MatLab

7. Основные элементы интерфейса

Command window – окно команд;
Command history – окно истории команд;
Current directory – окно, содержащие список
файлов и папок текущего каталога;
Editor – текстовый редактор;
Workspace – окно со списком переменных
текущей сессии.

8. Основные элементы интерфейса

Базовые команды редактора (Command window)
↑ – возврат к предыдущей команде.
help имя функции – справка по функции (или
F1).
clc – очистить окно команд (Command window).
clear – удалить все переменные в текущей
сессии.
Ctrl + C (в окне команд) прерывание
вычислений.
Ctrl+R, Ctrl+T – закомментировать часть

9. Типы файлов в MatLab

*.m (текстовые) содержат тексты программ,
определения функций.
*.mat (бинарные) содержат значения
переменных.
*.mex (бинарные). MEX-файлы – динамически
подключаемые библиотеки

10. Типы данных (массивы)

Вектор-строка, вектор-столбец

11. Типы данных (массивы)

Матрицы (одномерные массивы, двумерные
массивы)

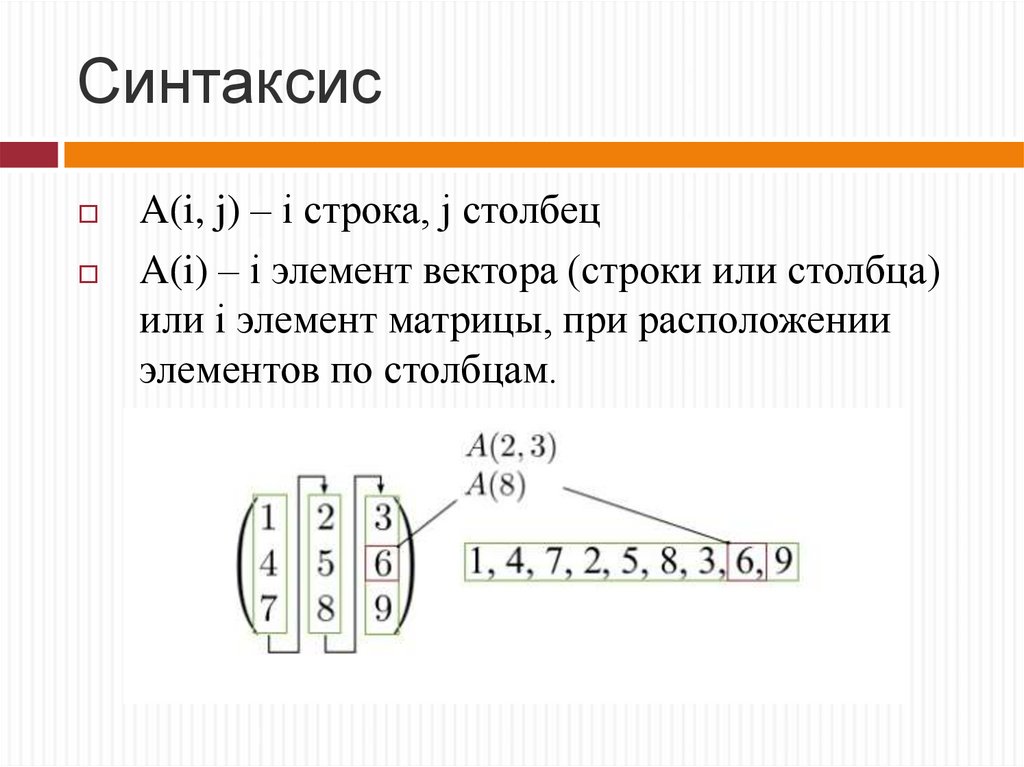
12. Синтаксис

A(i, j) – i строка, j столбец
A(i) – i элемент вектора (строки или столбца)
или i элемент матрицы, при расположении
элементов по столбцам.

13. Создание массивов

элементы вводятся построчно;
элементы матрицы в строке можно разделять
пробелами или запятыми;
для разграничения строк используются точка с
запятой.

14. Создание массивов

Для создания массивов:
1.
Квадратные скобки: a = [2, 4, 6, 8], a = [2 4 6
8], a = [2 4 6 8; 1 2 3 4]
2.
Выражение вида: а = 2:2:8, a= [2:2:8; 1:1:4]
3.
Использование циклов:
a(1)=2
for i=1:1:3
a(i+1)=a(i)+2
end

15. Пример 1

1.
2.
Создать массив, используя разные
способы:
Массив A содержит величины от 1 до 9
(три столбца, три строки).
Массив B содержит величины от 10 до 100
с шагом 10 (одна строка).

16. Простейшие вычисления

17. Пример 2

Рассчитать значение величины у по
формуле
a bx
y
c
при х = 2, если a = 4, b = 8, c = 10.

18. Операции на матрицами

A' – транспонирование матрицы
C=A/B – деление, умножение и др.
C=A./B – поэлементное деление (Ci = Ai/Bi)

19. Примеры

20. Поэлементные операции над матрицами

Т.к. векторы и матрицы хранятся в двумерных массивах, то
применение математических функций к матрицам и
поэлементные операции производятся так же, как для
векторов.
Единственное отличие – точка перед соответствующей
операцией.
Например, умножение каждого элемента одной матрицы на
соответствующий элемент другой производится при помощи
оператора .*
Для деления элементов первой матрицы на соответствующие
элементы второй используется оператор ./, а для деления
элементов второй матрицы на соответствующие элементы
первой служит .\

21. Пример 3

Рассчитать значение величины у по формуле
a bx
y
c
при х = 2, если a меняется от 2 до 8 с шагом 2, b = 8, c =
10.

22. Основы программирования в MatLab

Цикл
for count = start:step:final
команды MatLab
end
Пример, накопление суммы
S=0
for k = 1:1:3
S = S + 1/k
end

23. Пример 4

Используя цикл, рассчитать значение величины у по
формуле
a bx
y
c
при х = 2, если a меняется от 2 до 8 с шагом 2, b = 8, c =
10.

24. Пример 5

Что будет являться результатом цикла:

25. Пример 6

Что будет являться результатом цикла:
n=3
m=4
x = [1 2 3]

26. Основы программирования в MatLab

Условия
if <условие>
<команды>
end
if <условие>
<команды>
else<команды>
end
if <условие>
<команды>
elseif <условие>
<команды>
else <команды>
end

27. Основы программирования в MatLab

Пример 7
Что будет являться результатом цикла:
n=5
a=[2 4 5 6 7 8]

28. Пример 7

Пример 8
Задать значение величины x в интервале от 2 до 8 с
шагом 2. Рассчитать значение у =x^2 для х 4.
Использовать цикл и условие MatLab.

29. Пример 8

Графика в MatLab
1)
2)
3)
графика функций одной переменной,
трехмерная графика,
анимационная графика,

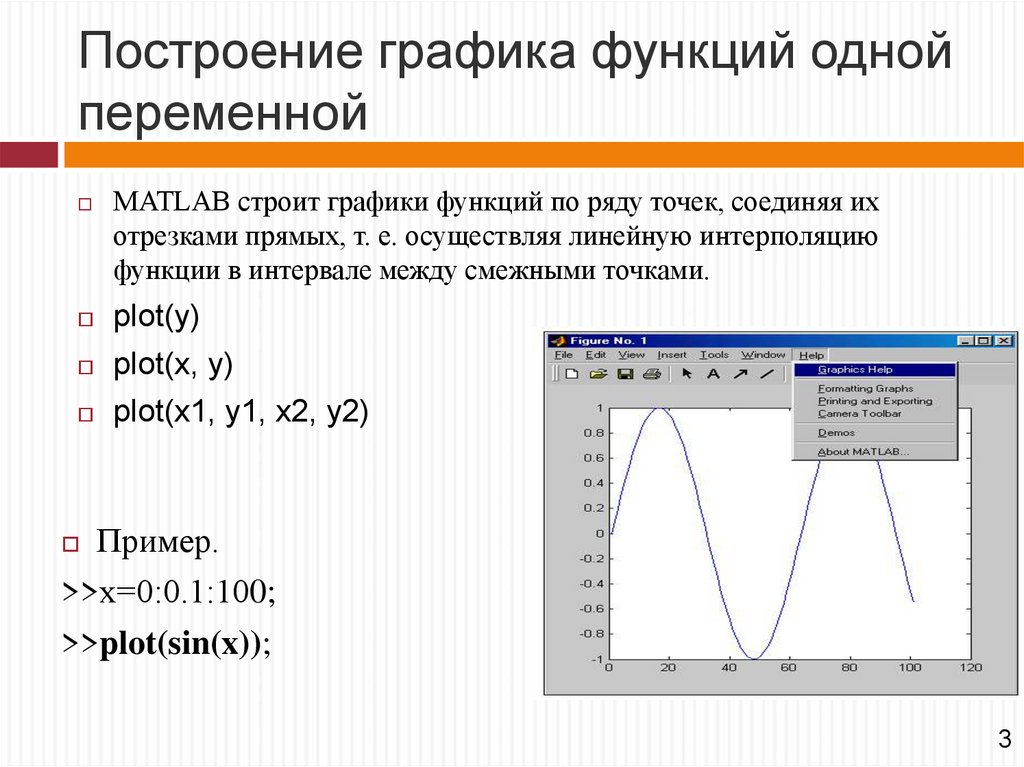
30. Графика в MatLab

Построение графика функций одной
переменной
MATLAB строит графики функций по ряду точек, соединяя их
отрезками прямых, т. е. осуществляя линейную интерполяцию
функции в интервале между смежными точками.
plot(y)
plot(x, y)
plot(x1, y1, x2, y2)
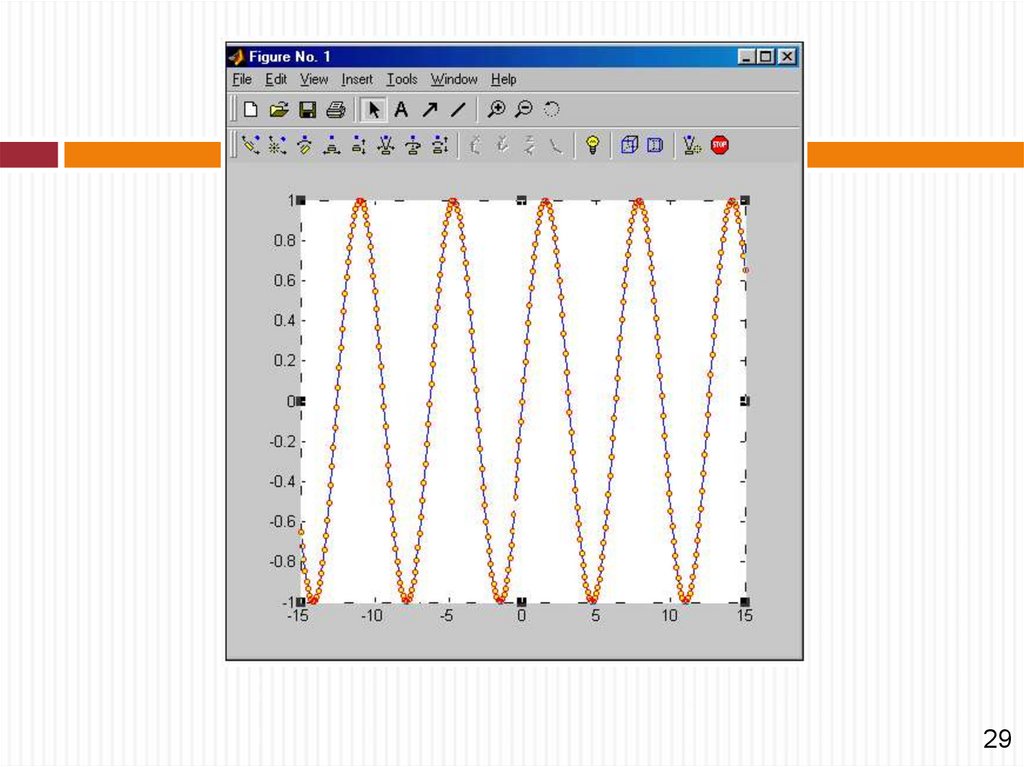
Пример.
>>х=0:0.1:100;
>>plot(sin(x));
3

31. Построение графика функций одной переменной

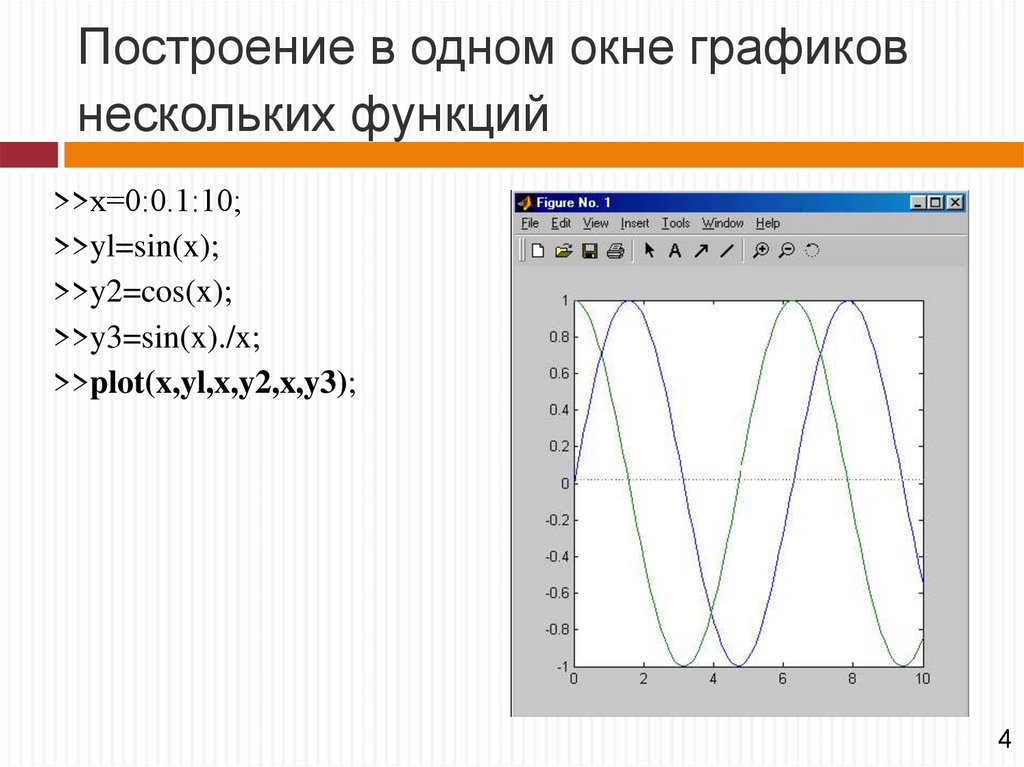
Построение в одном окне графиков
нескольких функций
>>х=0:0.1:10;
>>yl=sin(x);
>>y2=cos(x);
>>y3=sin(x)./x;
>>plot(x,yl,x,y2,x,y3);
4

32. Построение в одном окне графиков нескольких функций

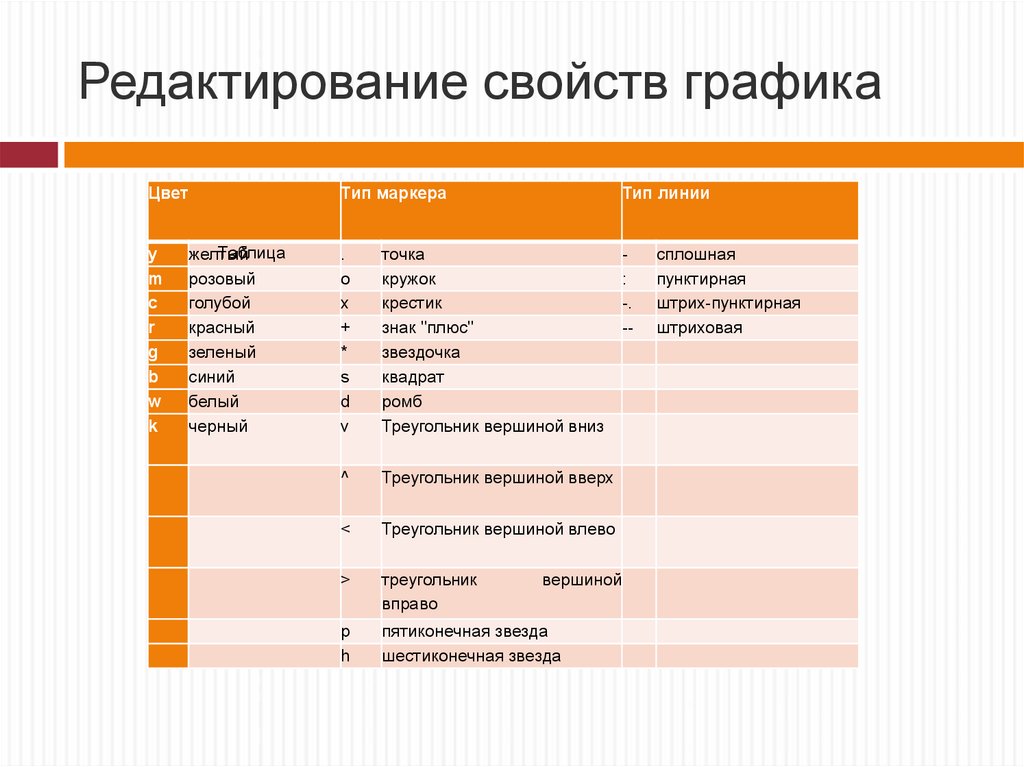
Редактирование свойств графика
Цвет
y
m
c
r
g
b
w
k
Тип маркера
Таблица
желтый
розовый
голубой
красный
зеленый
синий
белый
черный
Тип линии
.
o
х
+
*
s
d
v
точка
кружок
крестик
знак "плюс"
звездочка
квадрат
ромб
Треугольник вершиной вниз
^
Треугольник вершиной вверх
<
Треугольник вершиной влево
>
треугольник
вправо
p
h
пятиконечная звезда
шестиконечная звезда
:
-.
--
вершиной
сплошная
пунктирная
штрих-пунктирная
штриховая

33. Редактирование свойств графика

Пример
Если, например, необходимо построить первый график
красными точечными маркерами без линии, а второй
график - черной пунктирной линией, то следует
использовать команду
plot(x, f, 'r.', х, g, 'k:').

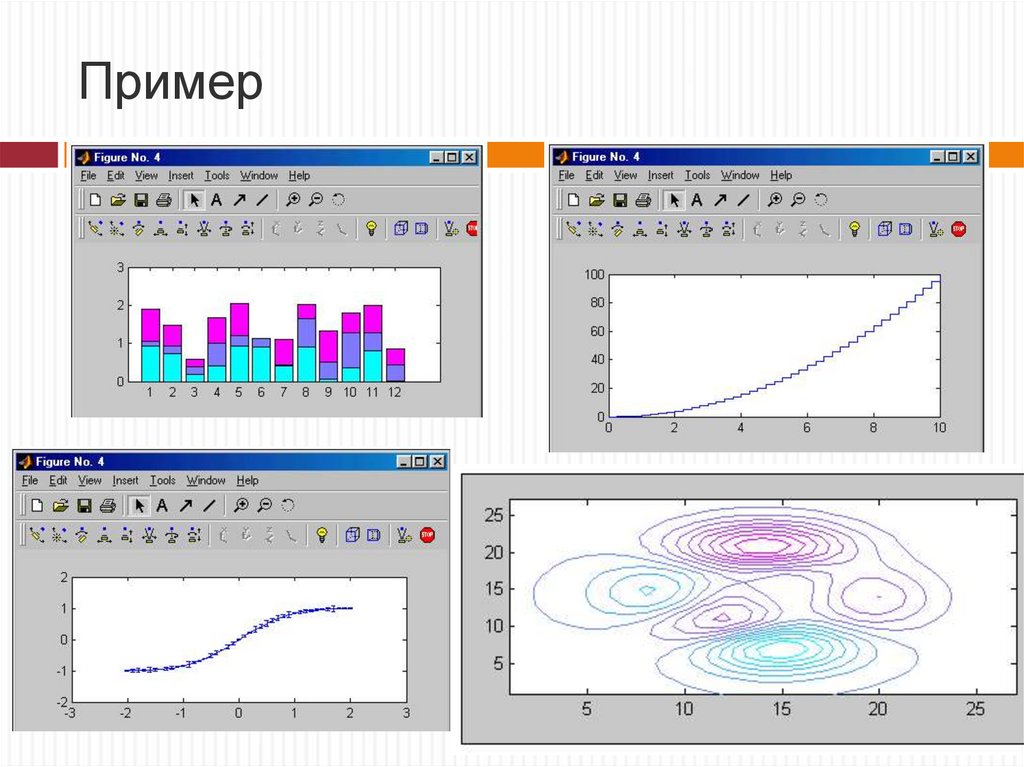
34. Пример

Другие типы графиков
bar(x, Y) – строит столбцовый график элементов вектора Y (или
группы столбцов для матрицы Y) со спецификацией положения
столбцов, заданной значениями элементов вектора х, которые
должны идти в монотонно возрастающем порядке;
stairs(Y) – строит лестничный график по данным вектора Y;
stairs(X,Y) – строит лестничный график по данным вектора Y с
координатами х переходов от ступеньки к ступеньке, заданными
значениями элементов вектора X;
errorbar(X,Y,L,U) – строит график значений элементов вектора Y
в зависимости от данных, содержащихся в векторе X, с
указанием нижней и верхней границ значений, заданных в
векторах L и U;
contour(Z) – строит контурный график по данным матрицы Z с
автоматическим заданием диапазонов изменения х и у.
5

35. Другие типы графиков

Пример
6

36. Пример

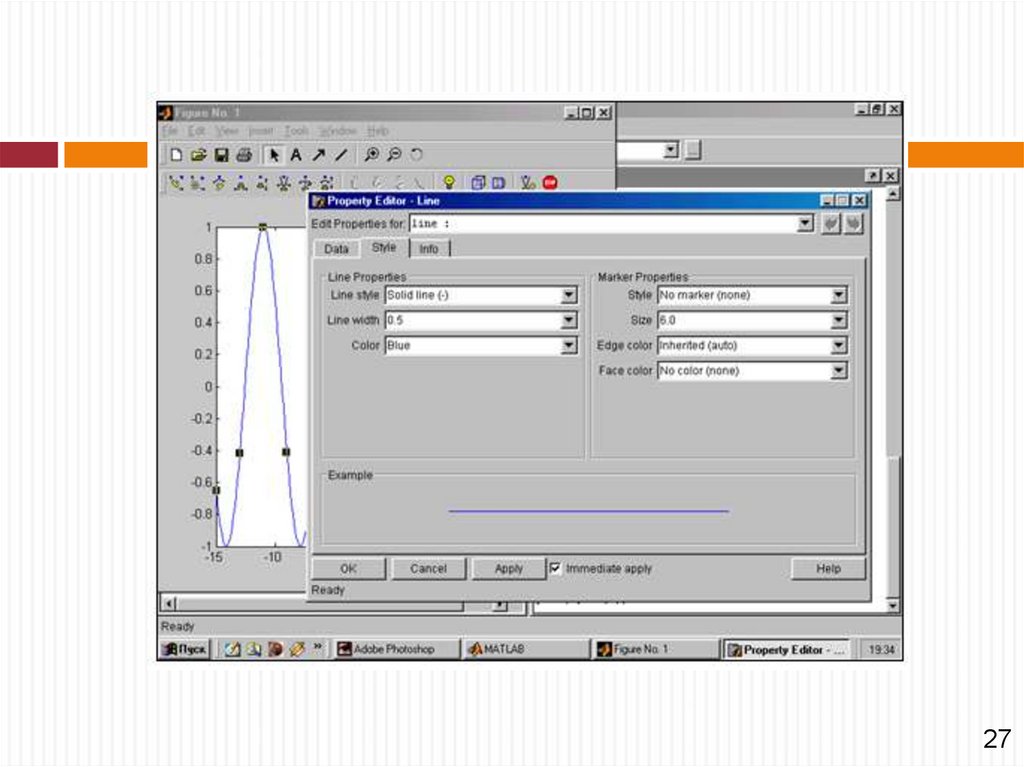
Основы форматирования двумерных
графиков
Форматирование линий графиков:
команды
Figure Properties (свойства фигуры) и
Axis Properties (свойства осей) со всеми необходимыми
настройками.
26

37. Основы форматирования двумерных графиков

27

38.

Форматирование маркеров опорных точек
Эти точки появляются на графике, если в поле свойств
маркера Marker Properties (Свойства маркера) из меню
Style (Стиль) выбрать стиль маркера, которые находятся
во вкладке Tools->Edit Plot/
Можно задавать размеры маркеров, цвет их закраски и
цвет окантовки.
Маркеры можно задавать в виде окружностей,
прямоугольников, крестиков, ромбиков и т. д. Применение
маркеров делает графики более наглядными.
28

39. Форматирование маркеров опорных точек

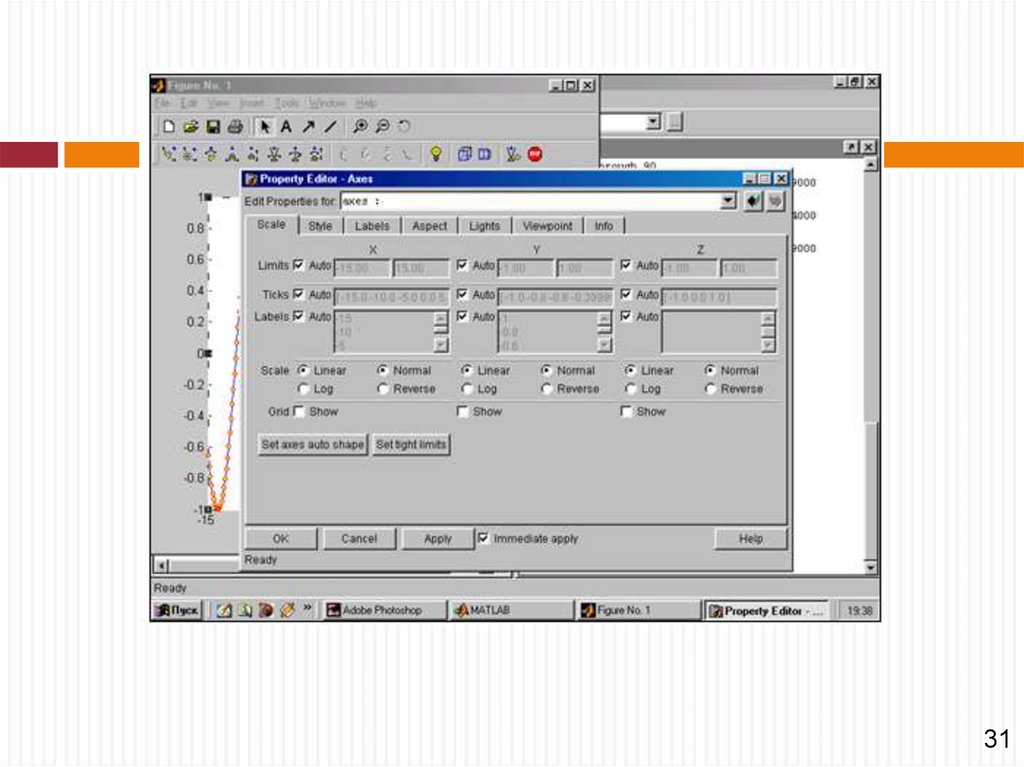
29

40.

Форматирование осей графиков
указав курсором мыши на оси графиков (на них тоже есть
метки в виде черных квадратиков) и дважды щелкнув
левой клавишей мыши, можно увидеть появление окна
форматирования объектов дескрипторной графики
Property Editor (Редактор свойств, Графический редактор
свойств), настроенного на форматирование осей.
30

41. Форматирование осей графиков

31

42.

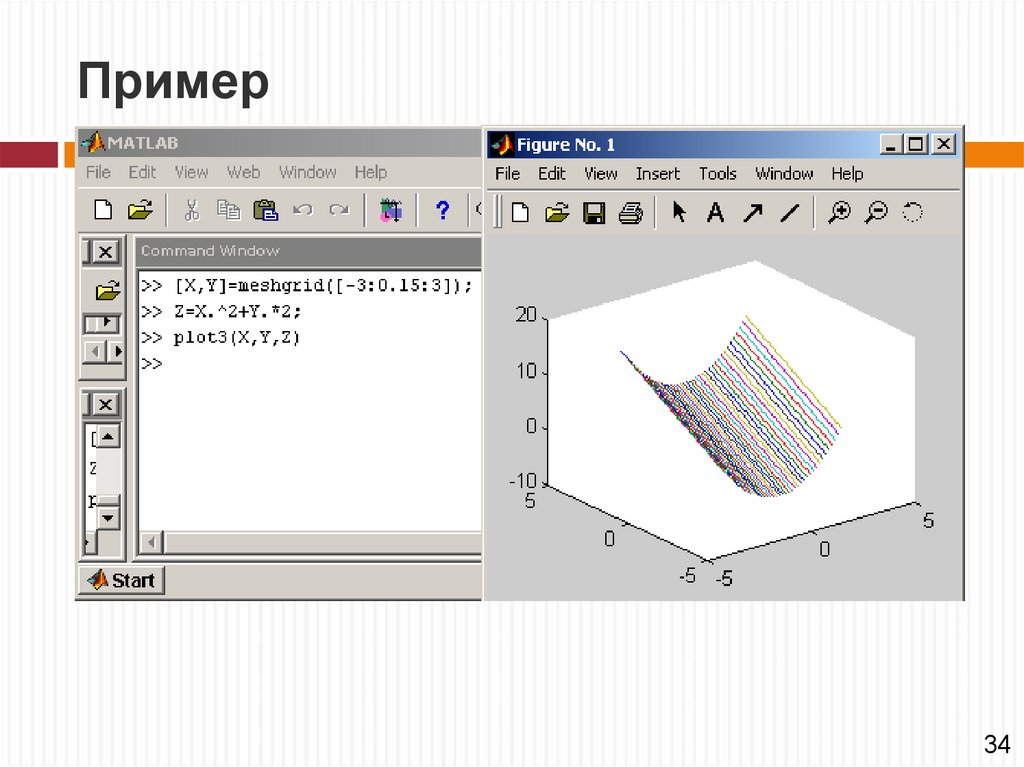
Построение графиков поверхностей
Команда plot3(...) является аналогом команды plot (...), но
относится к функции двух переменных z(x, у). Она строит
изображение трехмерных поверхностей и представлена
следующими формами:
plot3(x,y,z) – строит массив точек, представленных векторами
х, у и z, соединяя их отрезками прямых;
plot3(X,Y,Z), где X, Y и Z – три матрицы одинакового размера,
строит точки с координатами X(i.:), Y(i,:) и Z(i,:) и соединяет
их отрезками прямых;
plot3 (X, Y, Z, S) – обеспечивает построения, аналогичные
рассмотренным ранее, но со спецификацией стиля линий и
точек, соответствующей спецификации команды plot;
plot3(x1,y1,z1, s1,х2,у2,z2,s2,хЗ,уЗ,z3,s3,...) – строит на одном
рисунке графики нескольких функций z1(x1,y1), z2(x2,y2) и
т.д. со спецификацией линий и маркеров каждой из них.
32

43. Построение графиков поверхностей

Пример
34

44. Пример

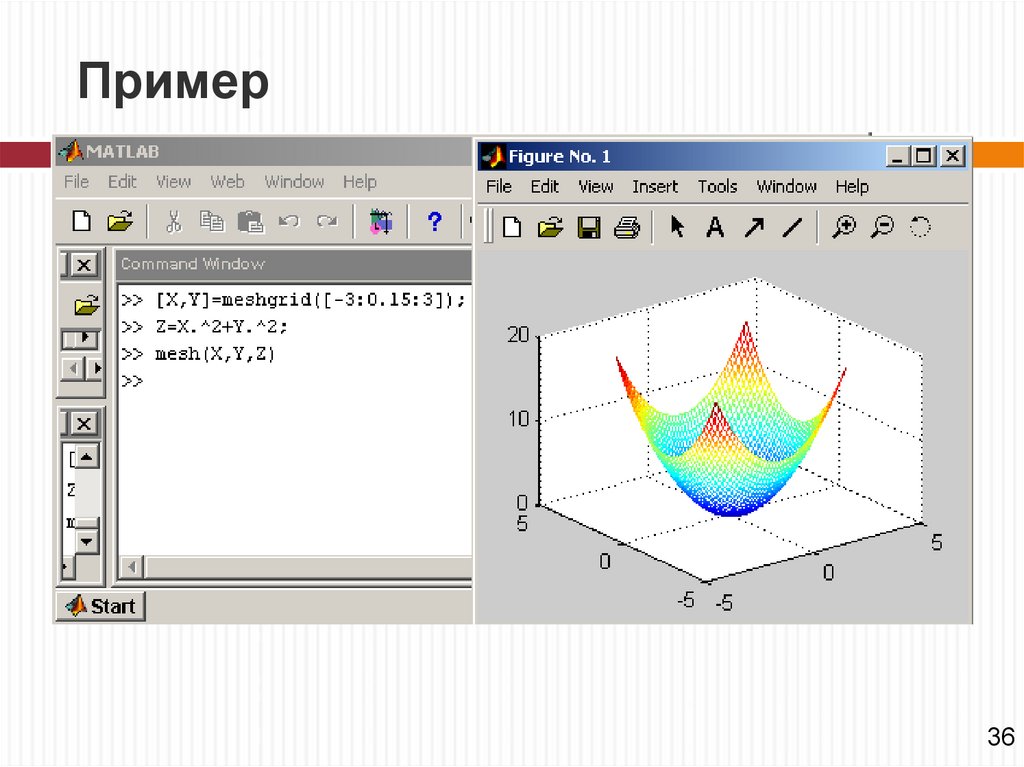
Сетчатые 3D-графики с окраской
Наиболее представительными и наглядными являются
сетчатые графики поверхностей с заданной или
функциональной окраской.
В названии их команд присутствует слово mesh. Имеются
три группы таких команд.
mesh(X,Y,Z,C) – выводит в графическое окно сетчатую
поверхность Z(X,Y) с цветами узлов поверхности,
заданными массивом С;
mesh(X,Y,Z) – аналог предшествующей команды при C=Z.
В данном случае используется функциональная окраска,
при которой цвет задается высотой поверхности.
35

45. Сетчатые 3D-графики с окраской

Пример
36

46. Пример

Построение поверхности с окраской
Особенно наглядное представление о поверхностях дают
сетчатые графики, использующие функциональную
закраску ячеек.
Например, цвет окраски поверхности z(x, у) может быть
поставлен в соответствие с высотой z поверхности с
выбором для малых высот темных тонов, а для больших
– светлых.
Для построения таких поверхностей используются
команды класса surf (...):
surf (X, Y, Z,С) – строит цветную параметрическую
поверхность по данным матриц X, Y и Z с цветом,
задаваемым массивом С;
37

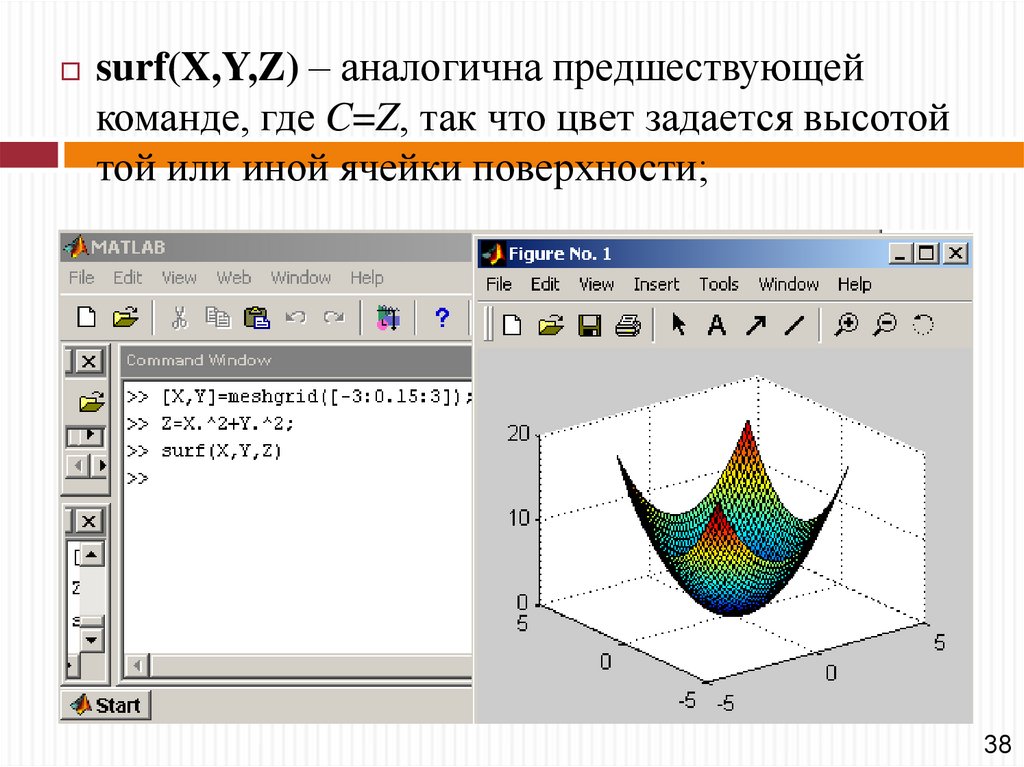
47. Построение поверхности с окраской

surf(X,Y,Z) – аналогична предшествующей
команде, где C=Z, так что цвет задается высотой
той или иной ячейки поверхности;
38

48.

Трехмерные контурные графики
Трехмерный контурный график представляет собой
расположенные в пространстве линии равного уровня,
полученные при расслоении трехмерной фигуры рядом
секущих плоскостей, расположенных параллельно
опорной плоскости фигуры.
При этом в отличие от двумерного контурного графика
линии равного уровня отображаются в аксонометрии.
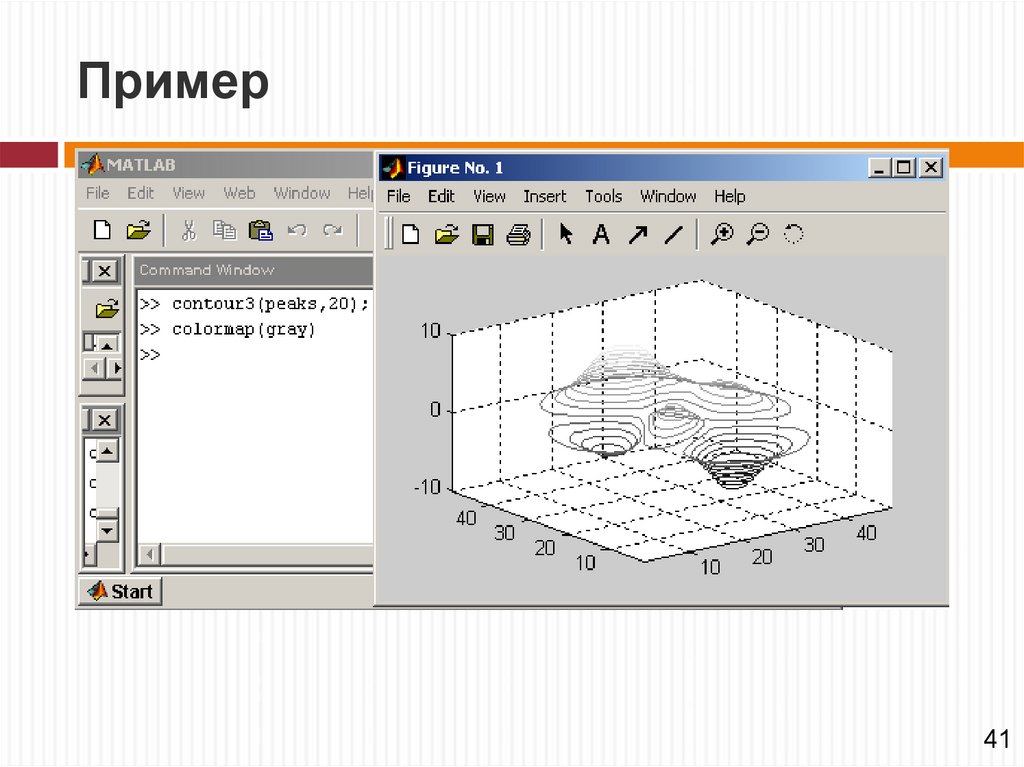
contour3(Z) – строит контурные линии для
поверхности, заданной массивом Z, без учета диапазона
изменения х и у;
39

49. Трехмерные контурные графики

contour3(Z,n) – строит то же, что предыдущая команда, но
с использованием n секущих плоскостей (по умолчанию
n=10);
contour3(X,Y,Z) – строит контурные линии для
поверхности, заданной массивом Z, с учетом изменения х
и у. Двумерные массивы X и Y создаются с помощью
функции meshgrid;
contours(X,Y,Z,n) – строит то же, что предыдущая
команда, но с использованием n секущих плоскостей.
40

50.

Пример
41

51. Пример

Анимационная графика
Движение точки на плоскости
Для отображения движения точки по траектории используется
команда comet.
При этом движущаяся точка напоминает ядро кометы с
хвостом.
Формы представления команды comet:
comet (Y) – отображает движение «кометы» по траектории,
заданной вектором Y;
comet3(Z) – отображает движение точки с цветным
«хвостом» по трехмерной кривой, определенной
массивом Z;
comet3 (X,Y,Z) – отображает движение точки «кометы» по
кривой в пространстве, заданной точками [X(i),Y(i), Z(i)];
comet3(X,Y,Z,p) – аналогична предшествующей команде
с заданием длины «хвоста кометы» как p*length(Z). По
42
умолчанию параметр р равен 0,1.

52. Анимационная графика

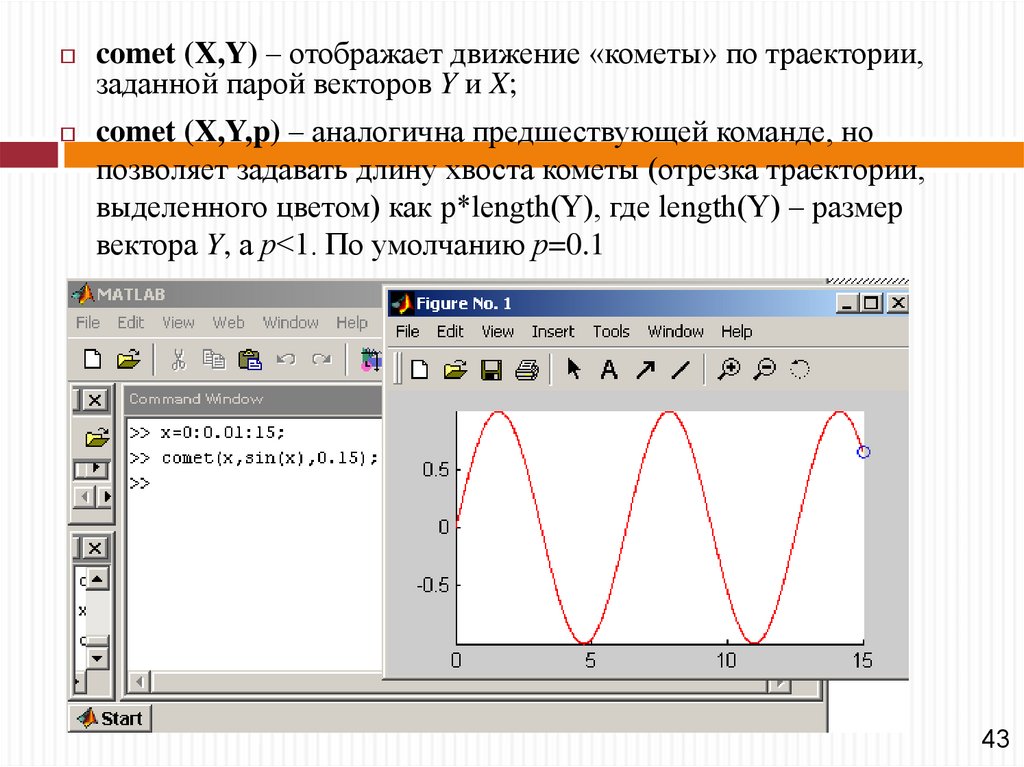
comet (X,Y) – отображает движение «кометы» по траектории,
заданной парой векторов Y и X;
comet (X,Y,p) – аналогична предшествующей команде, но
позволяет задавать длину хвоста кометы (отрезка траектории,
выделенного цветом) как p*length(Y), где length(Y) – размер
вектора Y, а р<1. По умолчанию р=0.1
43

53.

Основные средства анимации
Для более сложных случаев анимации возможно
применение техники мультипликации.
Техники мультипликации сводится к построению ряда
кадров изображения, при этом каждый кадр появляется
на некоторое время, затем стирается и заменяется на
новый кадр, несколько отличающийся от
предшествующего.
Если это отличие незначительно, то создается иллюзия
плавного перемещения объекта.
45

54. Основные средства анимации

Пример
https://www.youtube.com/watch?v=fnhzXrjX3WI

55. Пример

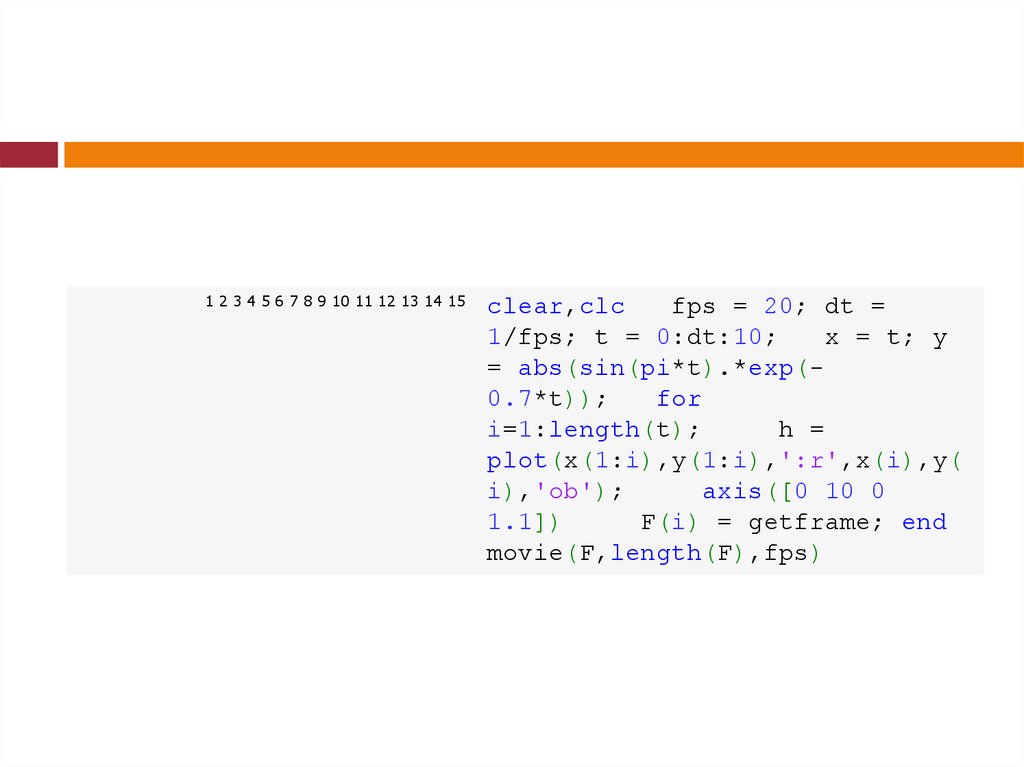
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
clear,clc
fps = 20; dt =
1/fps; t = 0:dt:10;
x = t; y
= abs(sin(pi*t).*exp(0.7*t));
for
i=1:length(t);
h =
plot(x(1:i),y(1:i),':r',x(i),y(
i),'ob');
axis([0 10 0
1.1])
F(i) = getframe; end
movie(F,length(F),fps)