Похожие презентации:
3D-построения в MatLab
1. 3D-построения в MatLab
Бабулова Г.А., преподаватель кафедры ИС2. Цель
• Ознакомиться с командами дляпостроения 3D – графиков в системе
Matlab.
3. Трёхмерная (3D-) графика
3Трёхмерная (3D-) графика
График поверхности, построенный
кружками
Сетчатые 3D-графики с окраской
Построение поверхности столбцами
Оформление графика поверхности
Контурные графики
Цветные объемные круговые диаграммы
4.
45.
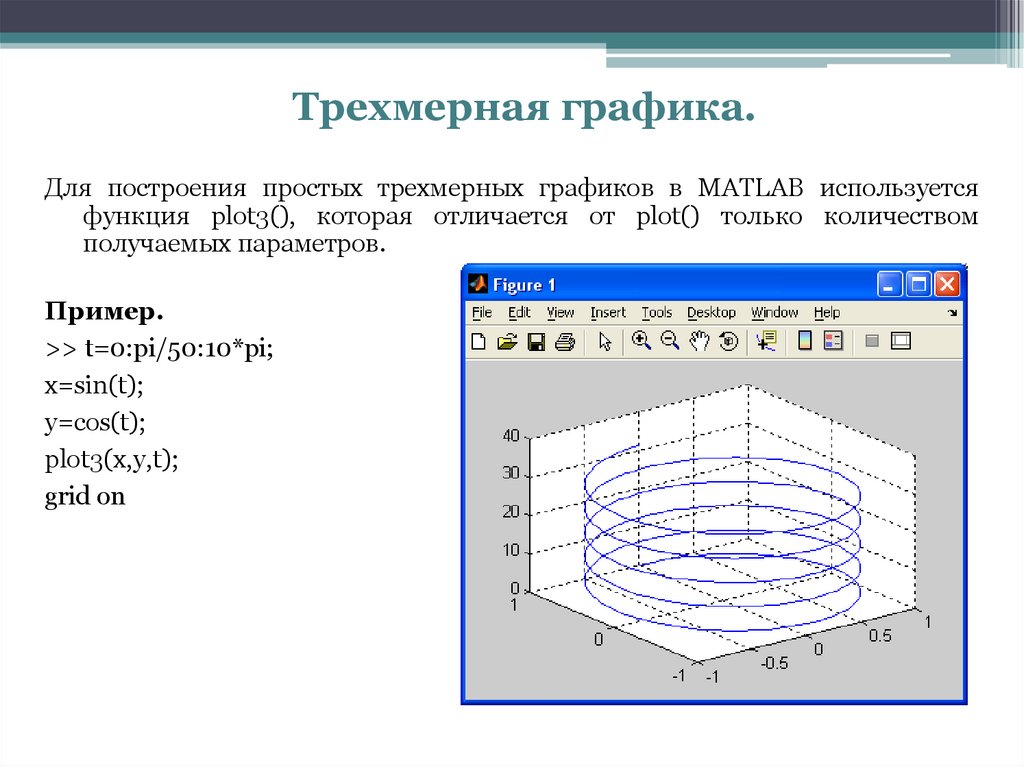
Трехмерная графика.Для построения простых трехмерных графиков в MATLAB используется
функция plot3(), которая отличается от plot() только количеством
получаемых параметров.
Пример.
>> t=0:pi/50:10*pi;
x=sin(t);
y=cos(t);
plot3(x,y,t);
grid on
6. Команда plot3
6Команда plot3
plot3(X,Y,Z) – строит поверхность в виде
линий, получаемых в сечении поверхности
плоскостями, параллельными плоскости yOz.
X, Y и Z – это матрицы: X,Y – задают узлы
сетки, а матрица Z – значения по оси z в этих
узлах.
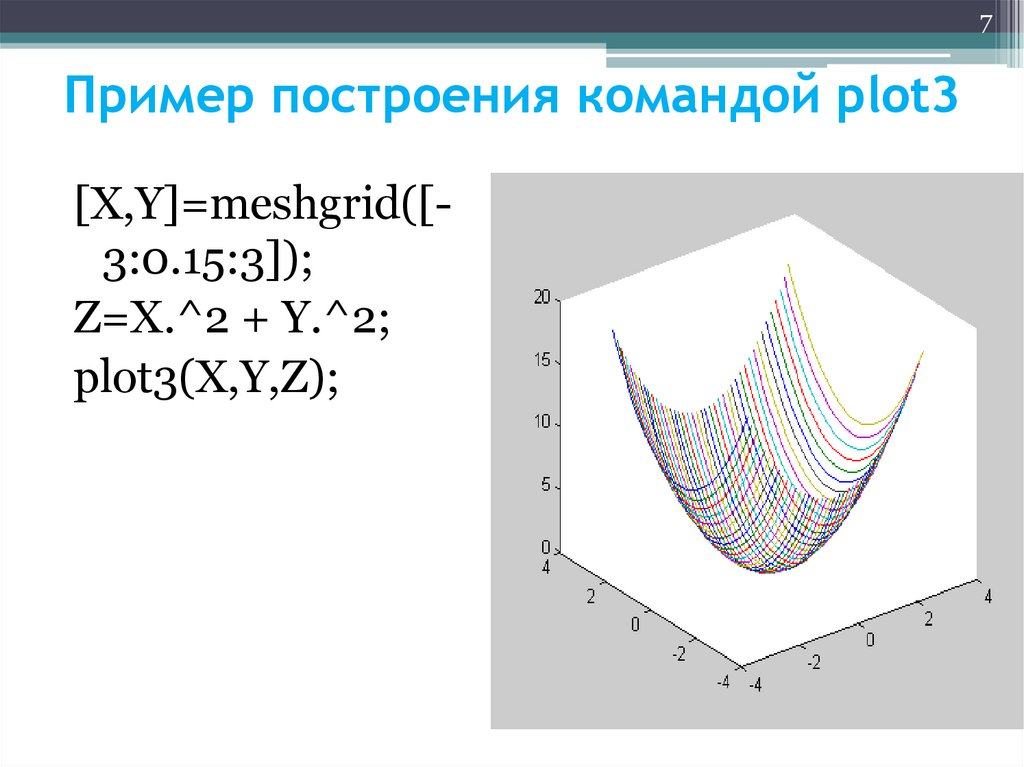
7. Пример построения командой plot3
7Пример построения командой plot3
[X,Y]=meshgrid([3:0.15:3]);
Z=X.^2 + Y.^2;
plot3(X,Y,Z);
8. Функция meshgrid
8Функция meshgrid
Функция meshgrid служит для создания
массивов данных для трехмерной графики.
Функция meshgrid возвращает две матрицы –
X и Y – которые определяют область
построения функции
9. Функция meshgrid записывается в следующих формах:
9Функция meshgrid записывается в
следующих формах:
• [X,Y] = meshgrid(x)
аналогична [X,Y] = meshgrid(x,x)
возвращает трехмерные массивы
• [X,Y] = meshgrid(x,y)
преобразует область, заданную
векторами х и у, в массивы X и Y
10.
10Пример:
[X,Y] = meshgrid(1:3,13:17)
X=
1
1
1
1
1
2
2
2
2
2
3
3
3
3
3
Y=
13
14
15
16
17
13
14
15
16
17
13
14
15
16
17
11.
11plot3 (X, Y, Z, S) — обеспечивает построения
с учетом спецификации стиля линий и точек
S, соответствующей спецификации команды
plot.
plot3 может строить на одном рисунке графики
нескольких функций z1(x1,y1), z2(x2, y2) и т. д.
со спецификацией линий и маркеров каждой
из них.
plot3(x1,y1,z1,s1, х2,у2,z2,s2,
хЗ,уЗ,z3,s3,...)
12.
12Стиль линий и точек команд plot и plot3
цвет
стиль точек
стиль линий
b синий
g зеленый
r красный
c циан
m фиолетовый
y желтый
k черный
w белый
. точка
- сплошная
o кружок
: пунктирная
x x-крестик
-. штрихпунктирная
+ плюс
-- штрихами
* звездочка
(none) без линий
s квадрат
d кристалл
v треугольник (вниз)
^ треугольник (вверх)
< треугольник (влево)
> треугольник (вправо)
p пятиугольник
h шестиугольник
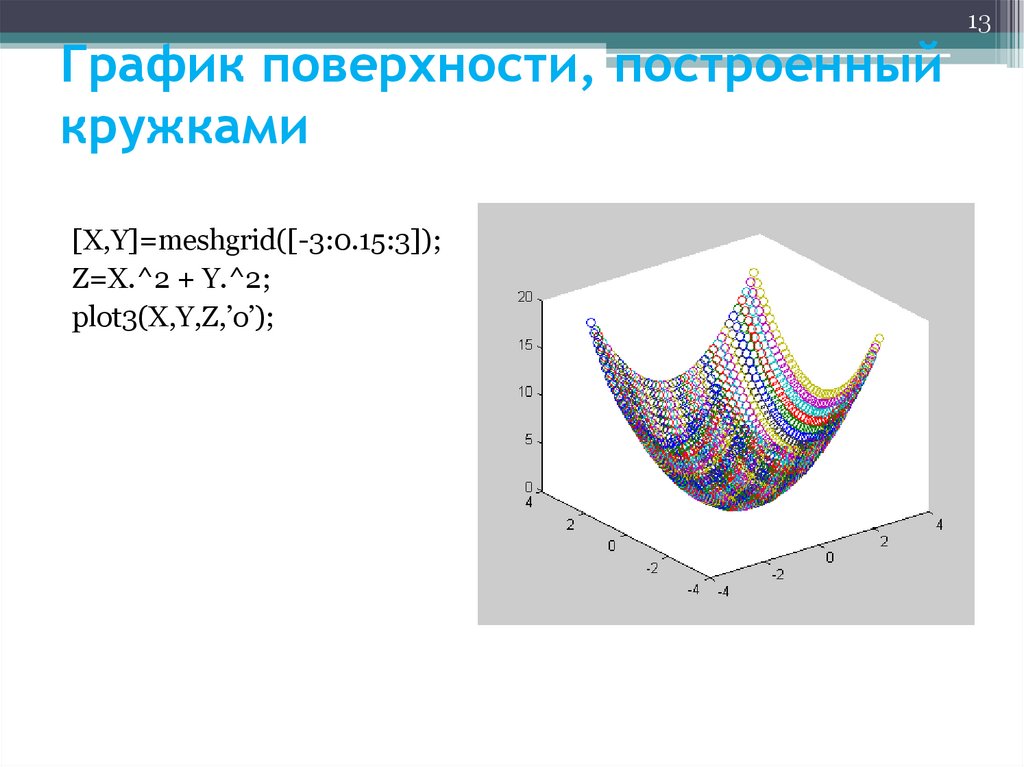
13. График поверхности, построенный кружками
[X,Y]=meshgrid([-3:0.15:3]);Z=X.^2 + Y.^2;
plot3(X,Y,Z,’o’);
13
14.
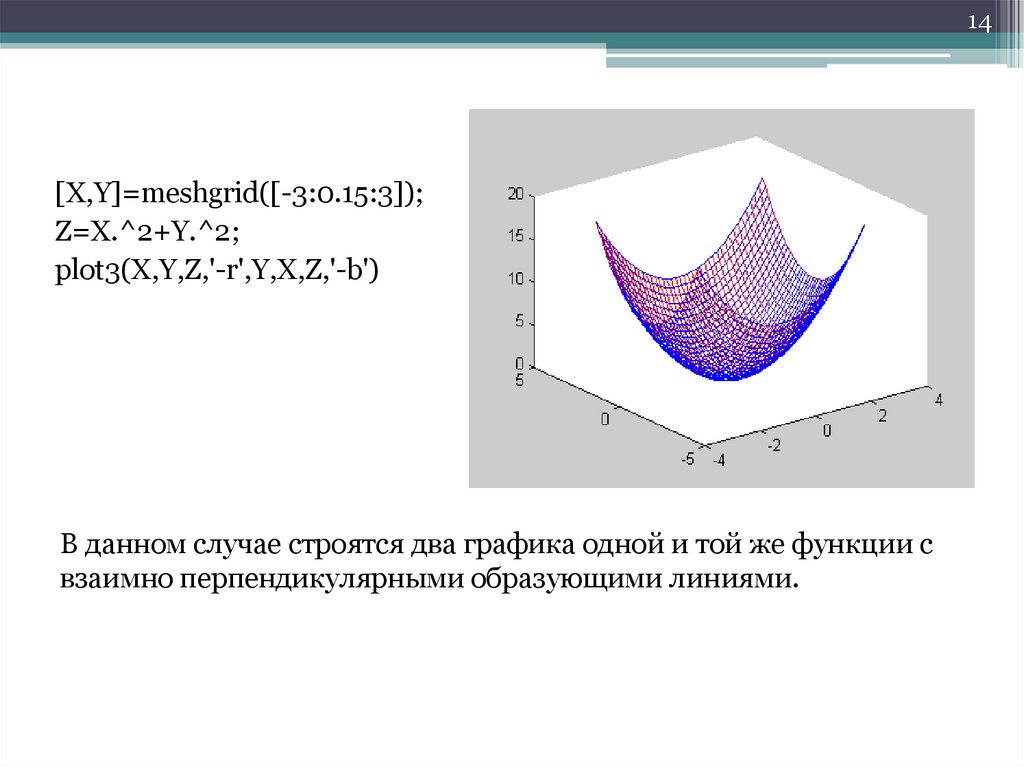
14[X,Y]=meshgrid([-3:0.15:3]);
Z=X.^2+Y.^2;
plot3(X,Y,Z,'-r',Y,X,Z,'-b')
В данном случае строятся два графика одной и той же функции с
взаимно перпендикулярными образующими линиями.
15. Сетчатые 3D-графики с окраской
15Сетчатые 3D-графики с окраской
Наиболее
представительными
и
наглядными
являются сетчатые графики поверхностей с заданной
или функциональной окраской. В названии их
команд присутствует слово mesh.
• mesh – выводит в графическое окно сетчатую
поверхность;
• meshc — помимо графика
изображение ее проекции;
поверхности
• meshz — строит поверхность в виде столбиков.
дает
16.
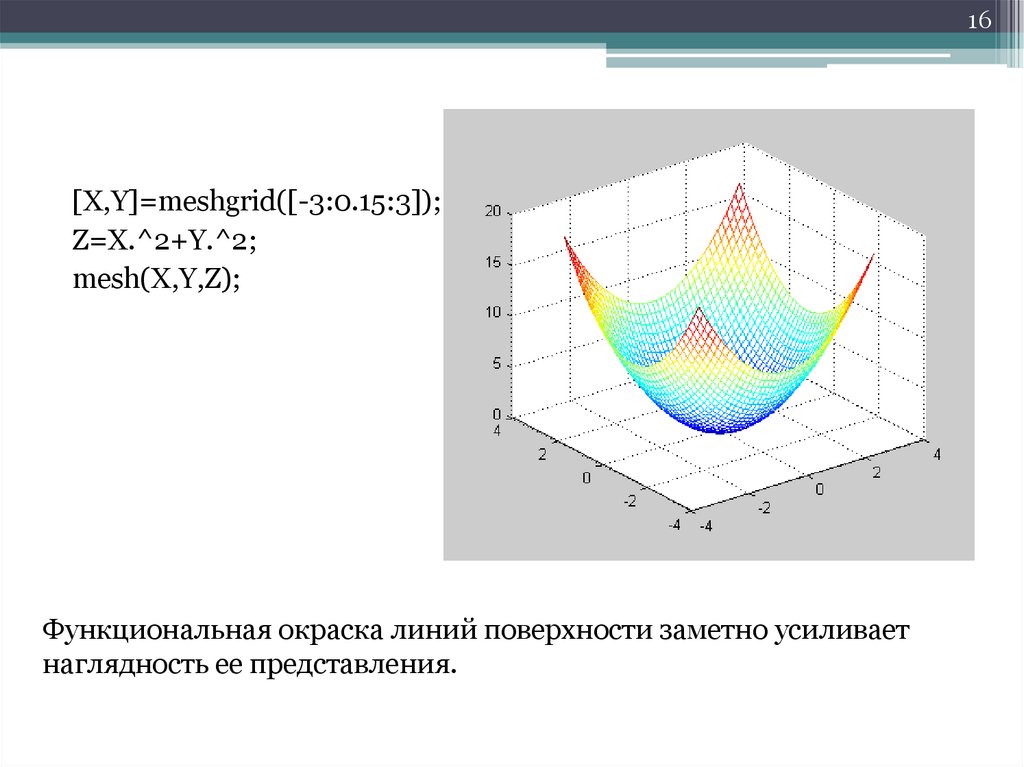
16[X,Y]=meshgrid([-3:0.15:3]);
Z=X.^2+Y.^2;
mesh(X,Y,Z);
Функциональная окраска линий поверхности заметно усиливает
наглядность ее представления.
17. Оформление графика поверхности
17Оформление графика поверхности
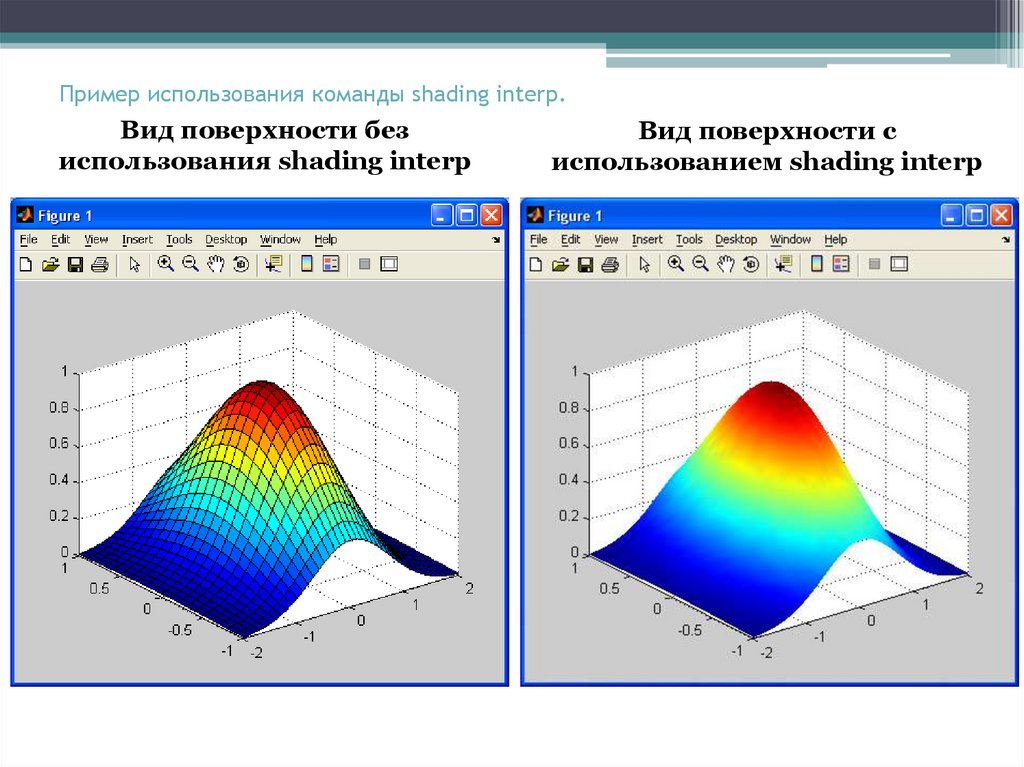
Для удаления с поверхности линий, изображающих
ребра, а также получения плавного перехода цветов
на освещенной поверхности, используется команда
shading interp
Для получения информации о всех свойствах
графического объекта, создаваемого функцией mesh,
используется команда get:
18. Пример использования команды shading interp.
Вид поверхности безиспользования shading interp
Вид поверхности с
использованием shading interp
19. Построение поверхности столбцами
19Построение поверхности
столбцами
Использование суффикса z приводит к
построению «графика с пьедесталом».
Поверхность строится из многочисленных
столбцов:
meshz(...)
20.
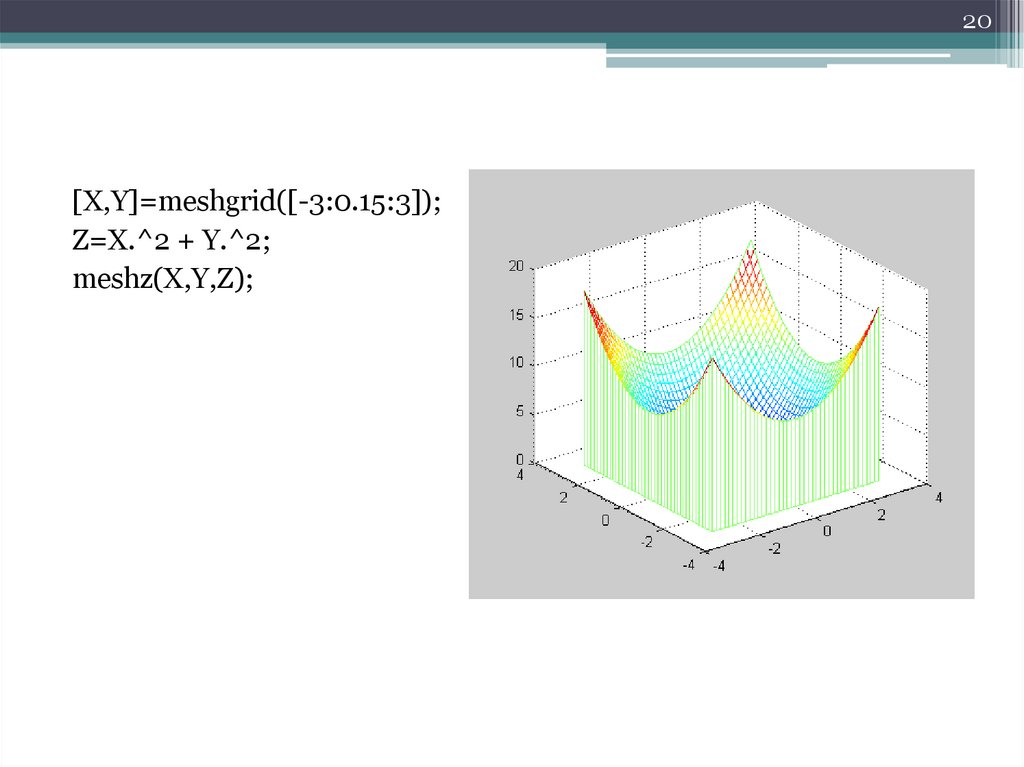
20[X,Y]=meshgrid([-3:0.15:3]);
Z=X.^2 + Y.^2;
meshz(X,Y,Z);
21.
Дополнительные деталиоформления 3D графиков
Для оформления трехмерных графиков можно
использовать те же функции, что использовались при
оформлении двумерных графиков функций,
рассмотренных ранее, такие как:
axis([ xmin, xmax, ymin, ymax, zmin, zmax ]), text,
xlabel, ylabel, zlabel, title.
С помощью функции subplot можно разместить в одном
графическом окне несколько трехмерных графиков.
22. Построение поверхности с окраской
22Построение поверхности с
окраской
Для построения поверхностей в виде сетчатых
графиков, использующих функциональную
закраску ячеек используются команды класса
surf(…).
23. Команды surf
23Команды surf
• surf — строит цветную параметрическую
поверхность;
• surfc – обеспечивает дополнительное
построение контурного графика проекции
фигуры на опорную плоскость;
• surfl
–
строит
график
цветной
поверхности с подсветкой от источника
света;
24. Построение 3D-поверхности
24Построение 3D-поверхности
• Рассмотрим пример:
построить поверхность f(x,y)=sin(r)/r, где
r=sqrt(x2+y2)
25.
25• Собственно поверхность выводится функцией surfl
26.
26[X,Y]=meshgrid([3:0.1:3]);
Z=sin(X)./(X.^2+Y.^
2+0.3);
surf(X,Y,Z);
shading interp;
colorbar;
В этом примере команда shading Interp обеспечивает устранение
изображения сетки и задает интерполяцию для оттенков цвета объемной
поверхности, а команда colorbar выводит шкалу цветовых оттенков.
27.
27Для повышения наглядности представления
поверхностей можно использовать
дополнительный график линий равного
уровня, получаемый путем проецирования
поверхности на опорную плоскость графика
(под поверхностью). Для этого используется
команда surfс:
28.
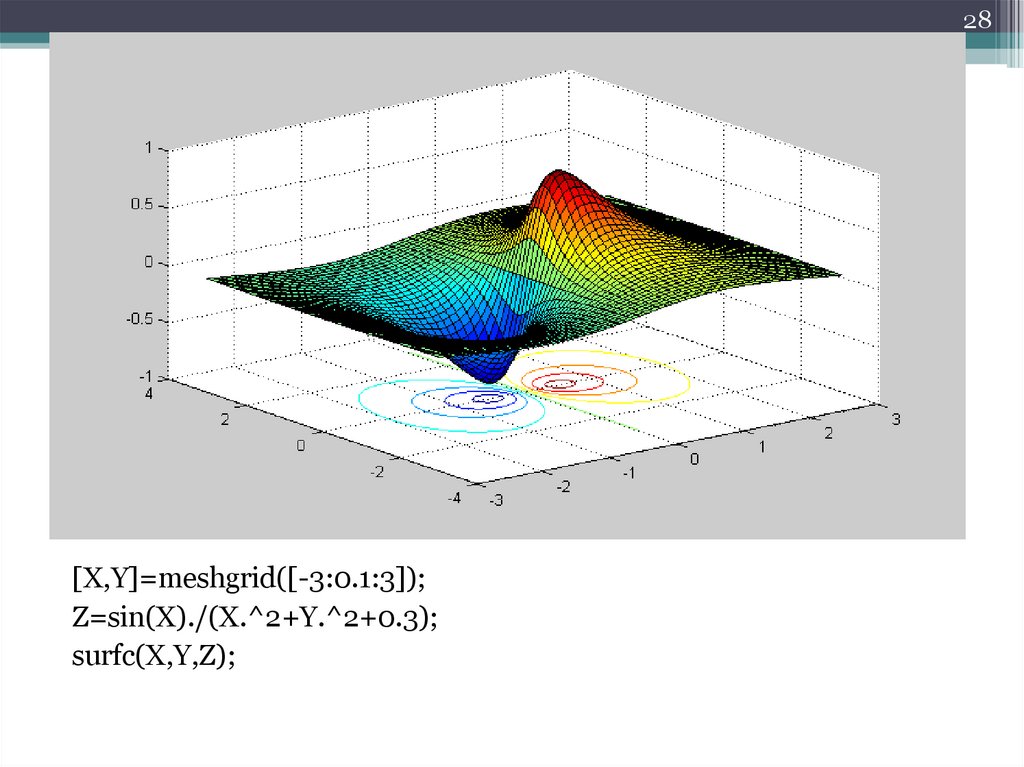
28[X,Y]=meshgrid([-3:0.1:3]);
Z=sin(X)./(X.^2+Y.^2+0.3);
surfc(X,Y,Z);
29. Контурные графики
29Контурные графики
[X,Y]=meshgrid([1:0.05:1]);
Z=X.^2+Y.^2;
levels=[0:0.1:0.5];
contour3(X,Y,Z,levels)
colorbar
Параметр levels
• может отсутствовать,тогда
число линий уровня
выбирается автоматически
• является просто значением
• является вектором значений
30. Контурные графики
30Контурные графики
• [X,Y]=meshgrid([1:0.05:1]);
• Z=X.^2+Y.^2;
• levels=[0:0.01:0.5];
• contour3(X,Y,Z,levels)
• colorbar
31.
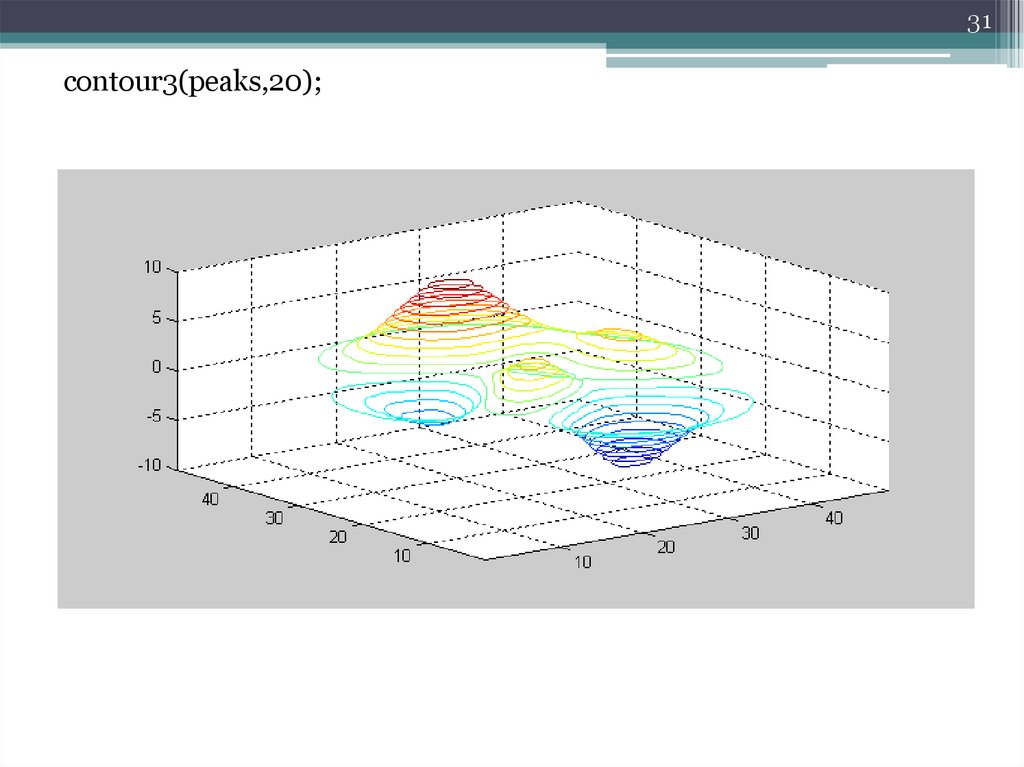
31contour3(peaks,20);
32. Контурные графики
32Контурные графики
• Разновидность контурного
графика contour(X,Y,Z)
• На плоскости xoy строятся
линии уровня. Сам график
поверхности не строится.
• В функции может стоять и 4ый
параметр,
который
указывает
число
линий
уровня.
• Для нанесения разметок на
линии уровня используется
clabel(CMatr,h)
• Cmatr
–
матрица,
содержащая информацию о
линиях уровня
• h – указатель на график, на
который следует нанести
разметку
33. contour
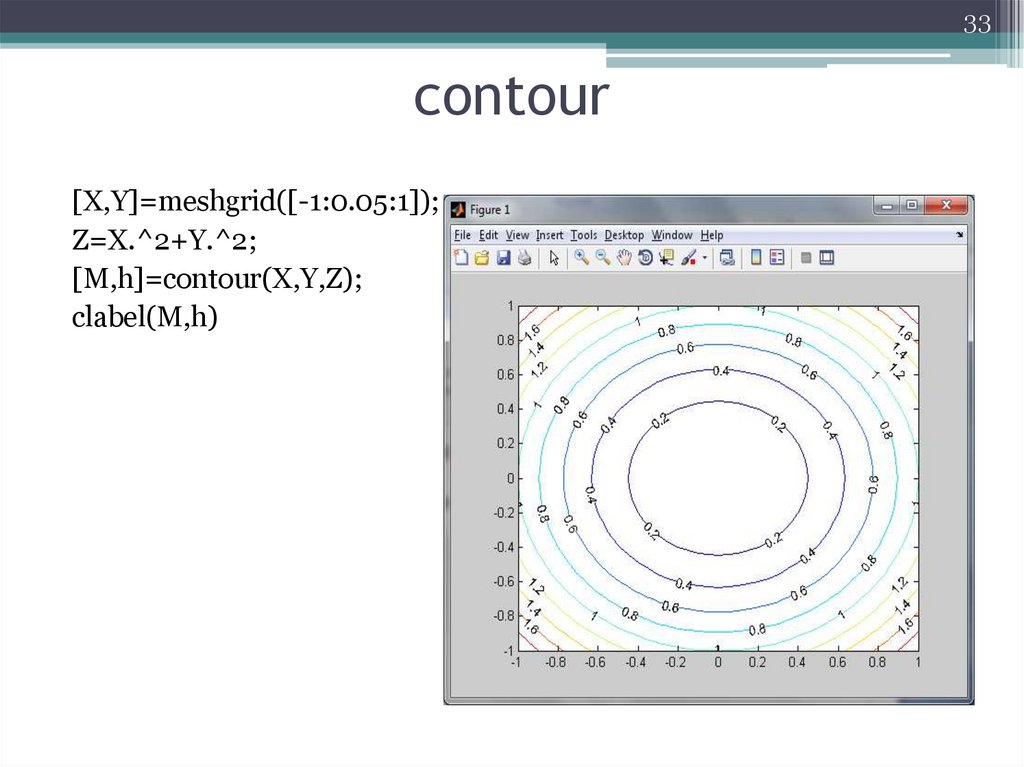
33contour
[X,Y]=meshgrid([-1:0.05:1]);
Z=X.^2+Y.^2;
[M,h]=contour(X,Y,Z);
clabel(M,h)
34. Цветные объемные круговые диаграммы
34Цветные объемные круговые
диаграммы
Для построения объемных круговых диаграмм
служит команда pie3:
x = [1 2.2 0.8 2.5 2];
pie3(x, [0 0 0 1 1])
35. MATLAB имеет несколько графических функций, возвращающих матричный образ поверхностей
35MATLAB имеет несколько графических
функций, возвращающих матричный образ
поверхностей
• peaks – поверхность с рядом пиков и впадин
• cylinder – цилиндрическая поверхность
• ellipsoid – поверхность элипсоида
• sphere – сферическая поверхность
36.
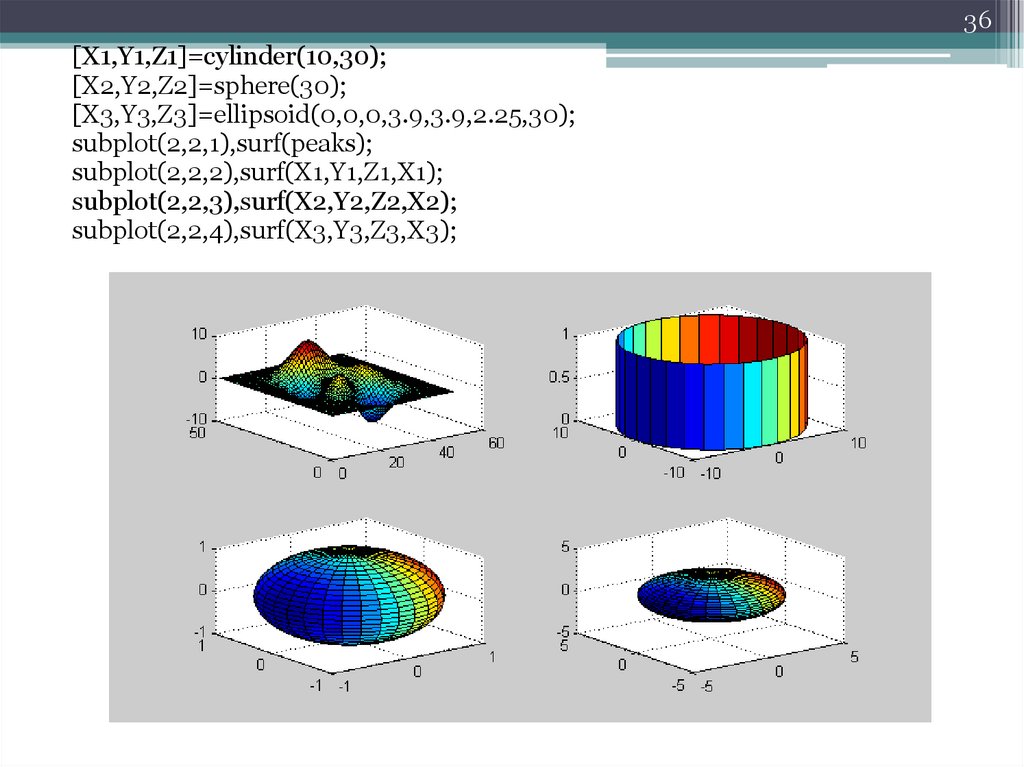
36[X1,Y1,Z1]=cylinder(10,30);
[X2,Y2,Z2]=sphere(30);
[X3,Y3,Z3]=ellipsoid(0,0,0,3.9,3.9,2.25,30);
subplot(2,2,1),surf(peaks);
subplot(2,2,2),surf(X1,Y1,Z1,X1);
subplot(2,2,3),surf(X2,Y2,Z2,X2);
subplot(2,2,4),surf(X3,Y3,Z3,X3);
37. Вывод графиков в отдельные окна
37Вывод графиков в отдельные окна
• figure– окно становится текущим
• clf– очистка всего текущего окна
• cla – очистить оси, заголовки и названия осей
• In=figure - Создание указателя на графическое окно
• figure(In) – переход к нужному окну
• clf(In) – очистка нужного окна
38. Функции для построения поверхностей
Функцияmesh, surf
38
Для чего используется
Построение поверхностей
meshc, surfc Строит поверхность и контурную диаграмму под ней
meshz
Поверхность на «пьедестале»
surfl
Подсвеченная поверхность
contour
Контурная диаграмма
plot3
Трёхмерная линия (параметрическое задание)
comet3
Движение по трёхмерной линии
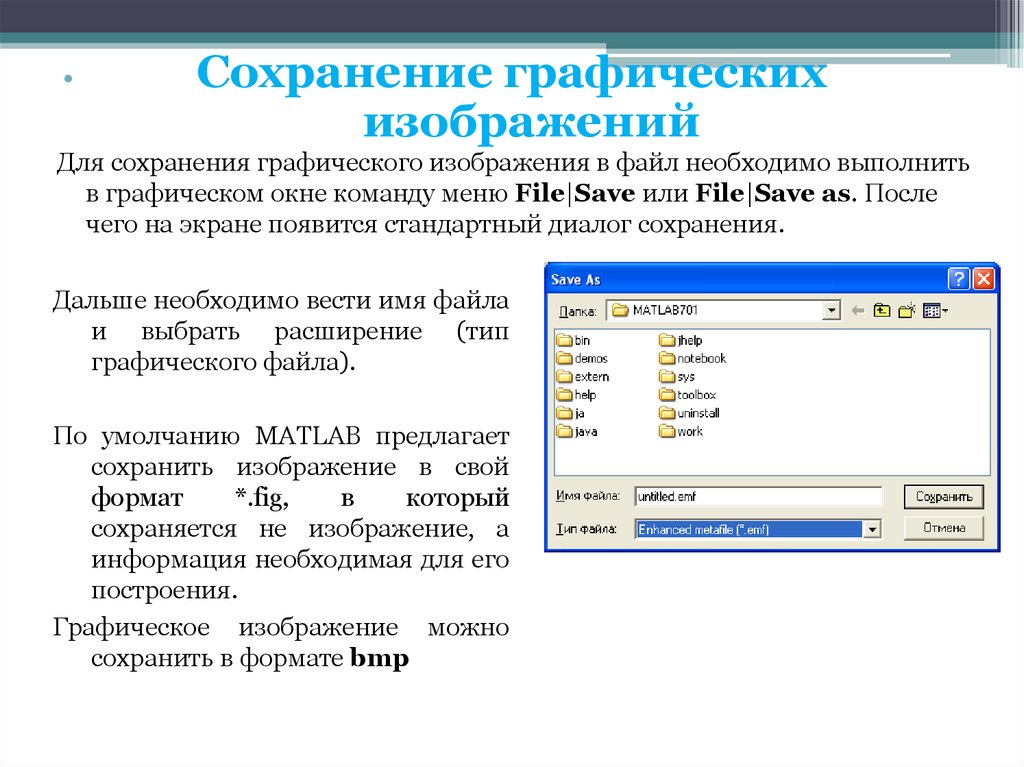
39. .
Сохранение графическихизображений
Для сохранения графического изображения в файл необходимо выполнить
в графическом окне команду меню File|Save или File|Save as. После
чего на экране появится стандартный диалог сохранения.
Дальше необходимо вести имя файла
и выбрать расширение (тип
графического файла).
По умолчанию MATLAB предлагает
сохранить изображение в свой
формат
*.fig,
в
который
сохраняется не изображение, а
информация необходимая для его
построения.
Графическое изображение можно
сохранить в формате bmp


























 Информатика
Информатика Программное обеспечение
Программное обеспечение








