Похожие презентации:
Синус и косинус суммы и разности
1. Синус и косинус суммы и разности.
2.
Найдите значениеsin 75
0
?
Ответить на данный
вопрос помогут
формулы синуса,
косинуса, тангенса
суммы и разности
аргументов
3.
Запоминаемsin x y sin x cos y cos x sin y
Синус суммы двух аргументов
равен произведению синуса
первого аргумента на косинус
второго плюс произведение
косинуса первого аргумента на
синус второго.
4.
Запоминаемcos x y cos x cos y sin x sin y
Косинус суммы двух аргументов
равен произведению косинусов
этих аргументов минус
произведение синусов этих
аргументов.
5.
Выведем формулу синуса разности двухаргументов
sin x y sin x ( y)
sin x cos( y ) cos x sin( y )
Учитывая, что sin( у ) sin y
cos( у ) cos y
получим,
sin x cos y cos x sin y
6.
Запоминаемsin x y sin x cos y cos x sin y
Синус разности двух аргументов
равен произведению синуса
первого аргумента на косинус
второго минус произведение
косинуса первого аргумента на
синус второго.
7.
Аналогично выведем формулу косинусаразности двух аргументов
cos x y cos x ( y)
cos x cos( y ) sin x sin( y )
cos x cos y sin x sin y
8.
Запоминаемcos x y cos x cos y sin x sin y
Косинус разности двух аргументов
равен произведению косинусов
этих аргументов плюс
произведение синусов этих
аргументов.
9.
Пример 1Вычислить:
sin 75 sin( 45 30 )
0
0
0
sin 45 cos 30 cos 45 sin 30
0
0
0
0
2 3
2 1
2 2
2 2
6
2
6 2
4
4
4
10.
Пример 2Вычислить:
cos 75 cos(45 30 )
0
0
0
cos 45 cos 30 sin 45 sin 30
0
0
0
0
2 3
2 1
2 2
2 2
6
2
6 2
4
4
4
11.
Пример 3Вычислить:
4
4
sin
cos cos
sin
15
15
15
15
Решение:
Заданное выражение можно «свернуть» в синус
суммы аргументов:
4
4
sin
cos cos
sin
15
15
15
15
3
4
sin
sin
3
2
15 15
12.
Пример 5Упростить выражение:
3 cos x sin x
Решение:
В заданном выражении вынесем множитель 2 за
скобки:
3
1
2
cos x sin x
2
2
Вспомним, что
3
1
cos ;
sin
2
6 2
6
13.
31
cos x sin x
3 cos x sin x 2
2
2
2 cos cos x sin sin x
6
6
2 cos x
6
14.
Повторим еще раз формулы:sin x y sin x cos y cos x sin y
sin x y sin x cos y cos x sin y
cos x y cos x cos y sin x sin y
cos x y cos x cos y sin x sin y
15. Решите из учебника
• № 481-484 нечетные16. Задание на дом
• § 28 выучить• № 481-487 (четные примеры), 488(1)
доделать








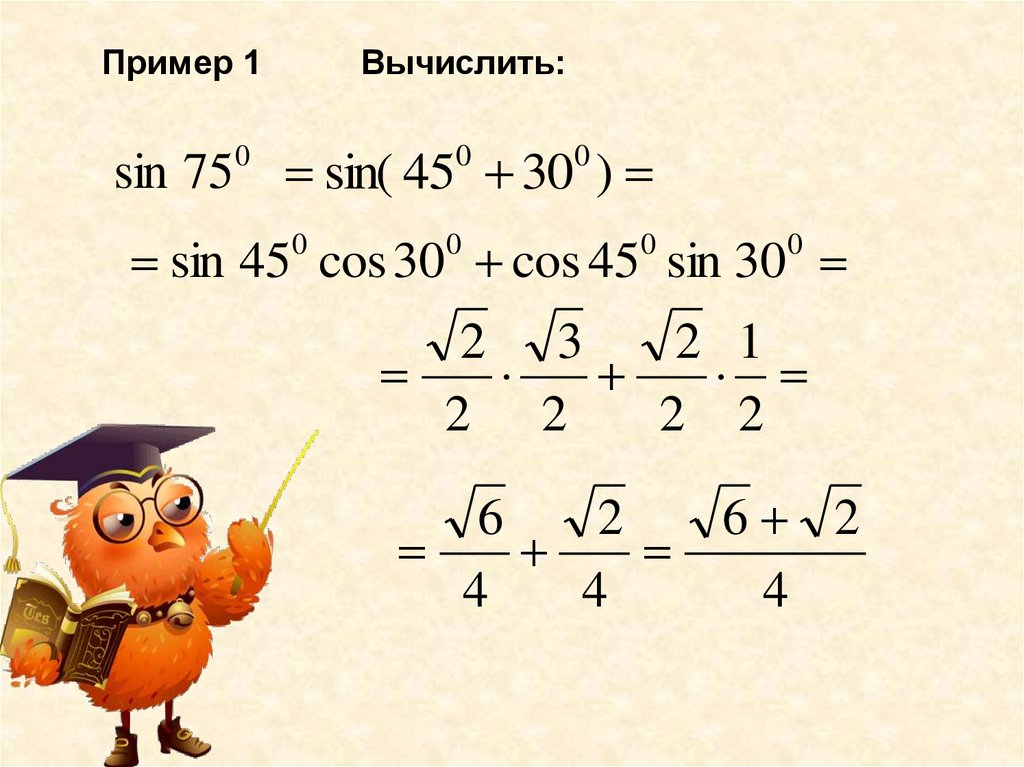
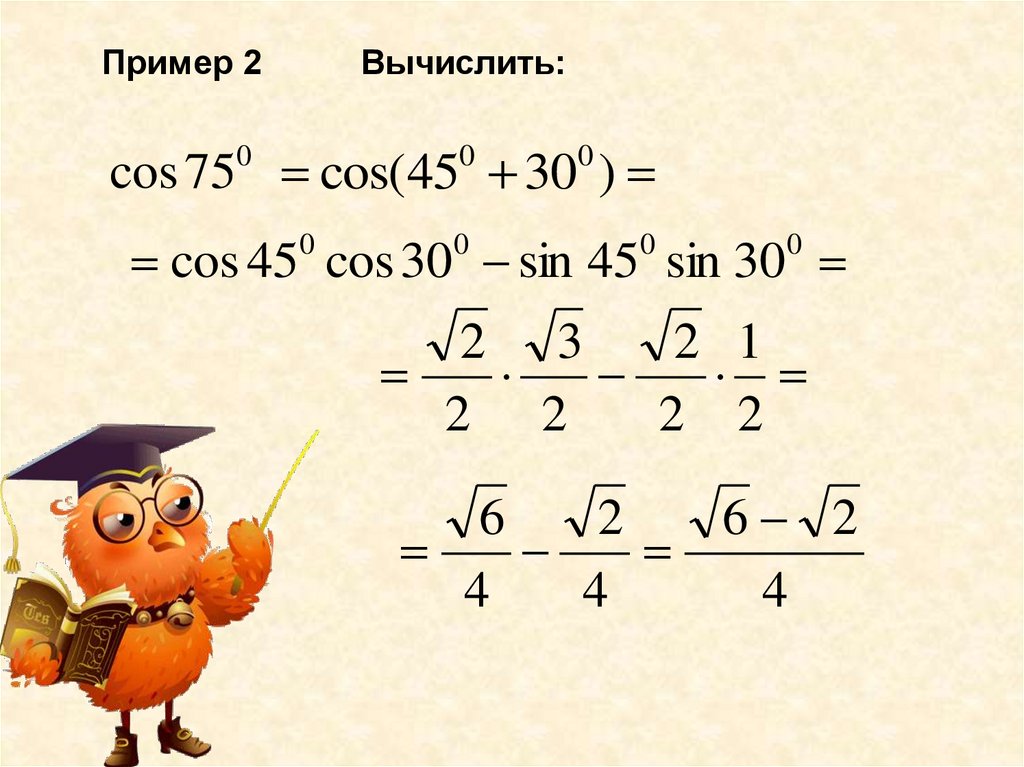


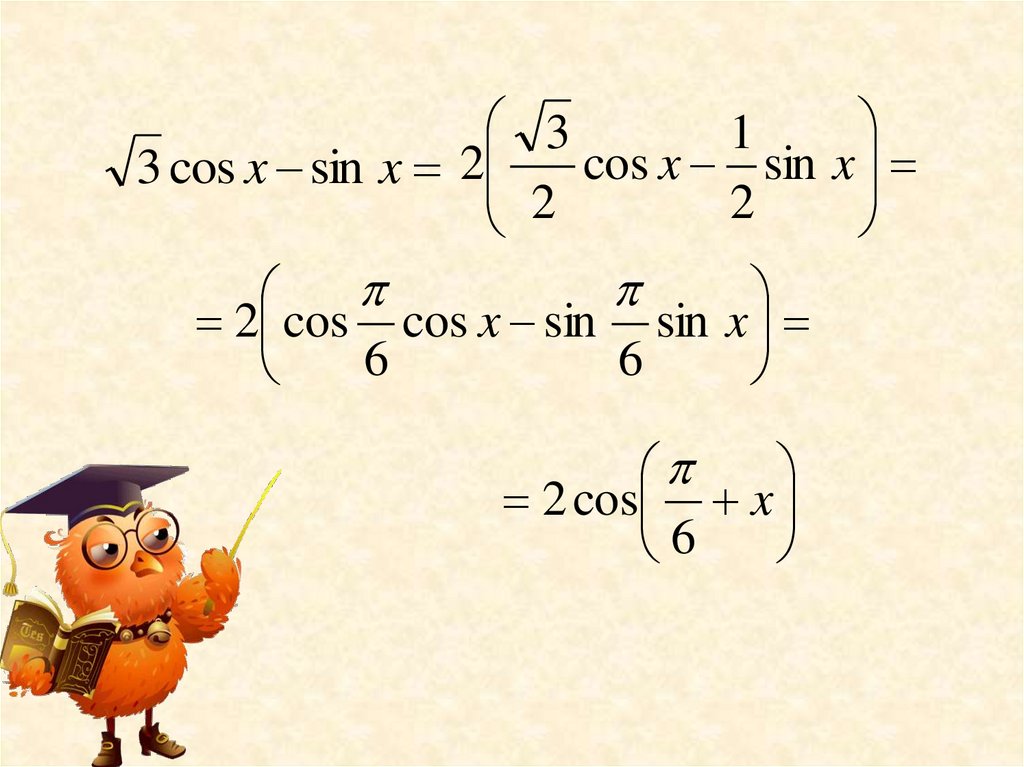



 Математика
Математика








