Аналитические вычисления в Matlab

1. Matlab

1

2. АНАЛИТИЧЕСКИЕ ВЫЧИСЛЕНИЯ В MATLAB

Содержание
Выход
2

3. Вычисления в Matlab

b
Пример: вычисление определённого f ( x)
a
интеграла
b
1. По формуле Ньютона: F(x)|a =F(b) – F(a),
где F(x) – первообразная
2.
получаем точный результат
но первообразную не всегда можно найти
Численно: методом прямоугольников,
трапеций, Симпсона и пр.
можно пользоваться даже тогда, когда интеграл
«не берётся»
но при вычислении возникают погрешности
Содержание
Выход
3

4. Средства Matlab для символьных вычислений

Изначально Matlab имел средства только
для численного анализа
Сегодня в Matlab встроены средства
аналитических (символьных) вычислений
Symbolic Math Toolbox
Является вычислительным ядром системы
Maple V
Установка Maple не требуется
Содержание
Выход
4

5. Создание символьных переменных

Для символьного анализа требуется создать
символьные переменные и функции
Символьные переменные создаются
по одной: x=sym(’x’)
○
так же можно создать целое символьное выражение
несколько сразу: syms x y z
Символьные функции определяются через
символьные переменные: f=x^2+y
Для построения символьных функций можно
воспользоваться командой ezplot
Представить в стандартной форме – командой
pretty
Содержание
Выход
5

6.

Содержание
Выход
6

7. Символьные вычисления

Преобразования математического анализа
дифференцирование,
пределы,
интегрирование,
разложение в ряд Тейлора
Упрощение и подстановки
Точная арифметика
Линейная алгебра
Решение уравнений и их систем
обычных и дифференциальных
Содержание
Выход
7

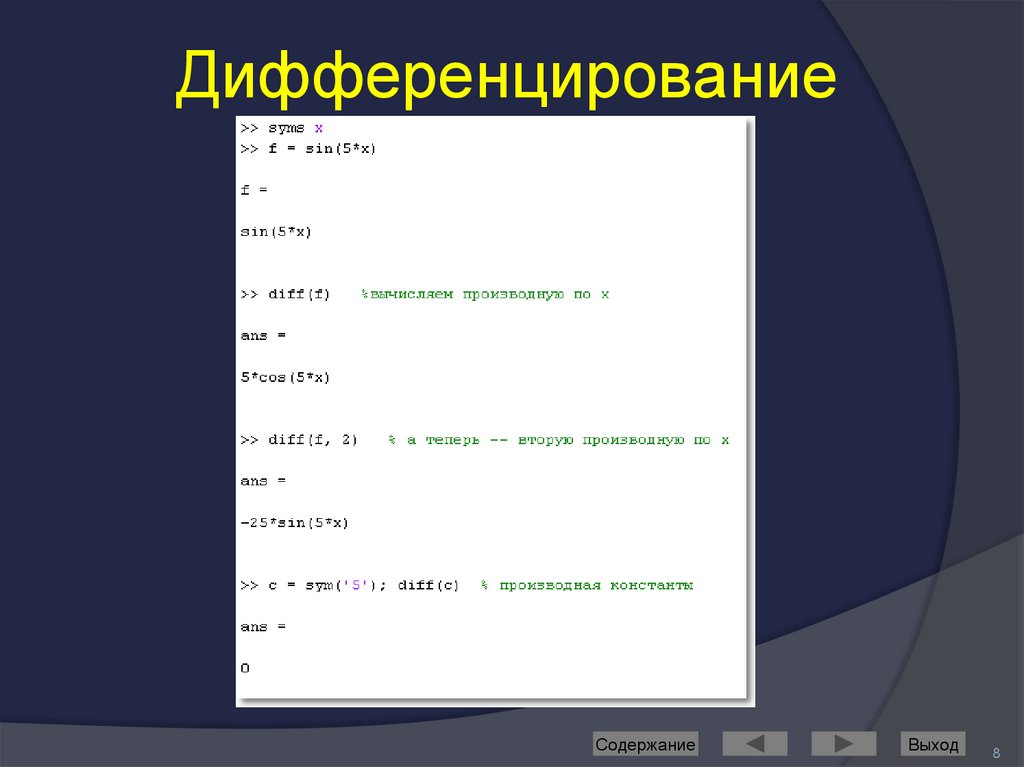
8. Дифференцирование

Содержание
Выход
8

9. Частные производные

Содержание
Выход
9

10.

Содержание
Выход
10

11. Пределы

Содержание
Выход
11

12. Односторонние пределы

Рассмотрим функцию f(x)=x/|x|
Содержание
Выход
12

13.

Содержание
Выход
13

14. Пределы (сводная таблица)

Содержание
Выход
14

15. Интегралы

Содержание
Выход
15

16. Интегралы с параметрами

Содержание
Выход
16

17.

~ -- это признак
действительного
числа
Содержание
Выход
17

18. Суммирование

Содержание
Выход
18

19. Разложение в ряд Тейлора

Попробуйте также
команду
taylortool
Содержание
Выход
19

20.

Содержание
Выход
20

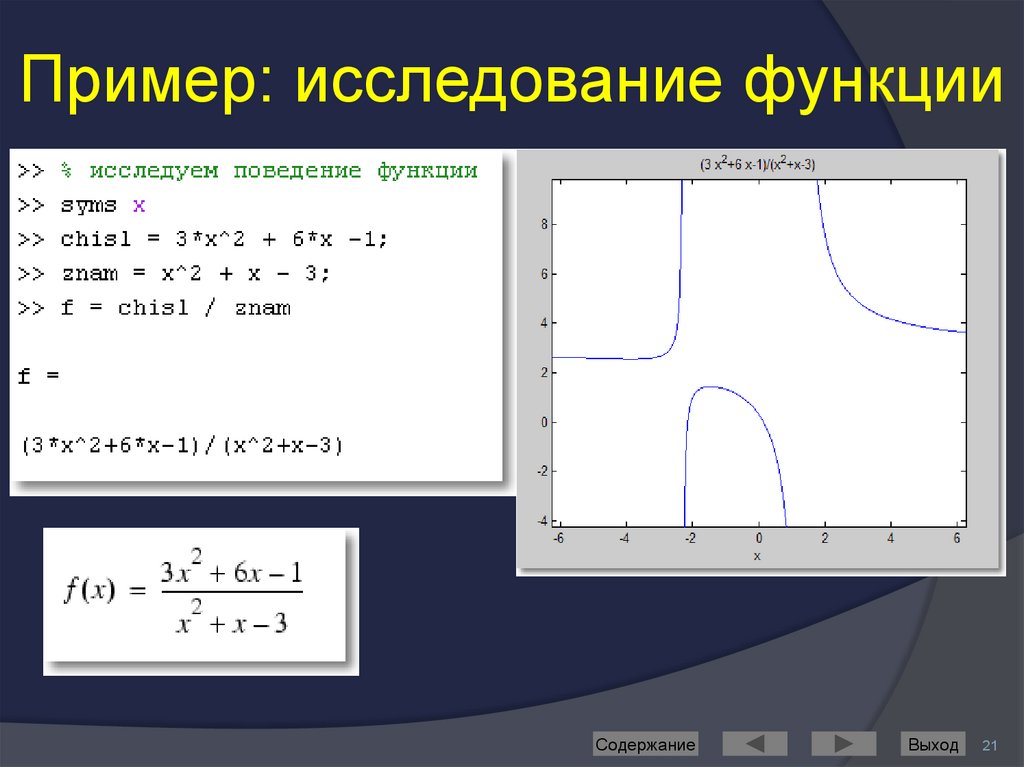
21. Пример: исследование функции

Содержание
Выход
21

22. Найдём горизонтальную асимптоту

Содержание
Выход
22

23. Найдём вертикальные асимптоты

Содержание
Выход
23

24. Код для построения асимптот

Содержание
Выход
24

25. Изображение асимптот

Содержание
Выход
25

26. Экстремумы функции

Содержание
Выход
26

27. Построение экстремумов

Содержание
Выход
27

28. Операции над полиномами

Реализуются при помощи функций
collect
expand
factor
horner
Содержание
Выход
28

29.

collect – вычисляет коэффициенты при
степенях независимой переменной
по умолчанию – x
Можно явно задать имя независимой
переменной в виде:
collect (f, VarName)
Содержание
Выход
29

30.

expand – представляет полином суммой
степеней без приведения подобных
Содержание
Выход
30

31.

factor – разлагает полином на множители,
если эти множители имеют рациональные
коэффициенты:
Содержание
Выход
31

32.

Также factor производит каноническое
разложение числа:
Содержание
Выход
32

33.

horner – представляет полином в схеме
Горнера:
Содержание
Выход
33

34. Упрощение выражений

simplify
реализует мощный алгоритм упрощения с
использованием тригонометрических, степенных,
логарифмических, экспоненциальных функций, а
также спецфункций (Бесселя, гипергеометрической,
интеграла ошибок и пр.)
simple
пытается получить выражение, которое
представляется меньшим числом символов, чем
исходное, последовательно применяя все функции
упрощения Symbolic Math Toolbox
Содержание
Выход
34

35. Simplify

Содержание
Выход
35

36. Simple

Содержание
Выход
36

37. Simplify против Simple

Иногда simple даёт более удачное решение,
чем simplify:
Содержание
Выход
37

38. Simple

simple особенно эффективна при работе с
тригонометрическими выражениями
Содержание
Выход
38

39. Подстановка

subs подставляет одно символьное
выражение в другое
Общий формат:
subs(<куда>, <вместо чего>, <что>)
Содержание
Выход
39

40. Пример подстановки

Содержание
Выход
40

41. Подстановка значения в функцию

Подстановка вместо переменной её
числового значения приводит к вычислению
символьной функции от значения аргумента
Содержание
Выход
41

42. Точная арифметика

Точные вычисления реализуются функцией
vpa (Variable-Precision Arithmetic)
Формат вызова:
vpa(<выражение>, <значащих цифр>)
Содержание
Выход
42

43.

Содержание
Выход
43

44. Решение уравнений и систем

Выполняет команда solve
До 4-го порядка включительно решаются
точно
Ответ выводится в степенях рациональных
чисел
Уравнения высших порядков и
трансцендентные, как правило, точно не
решаются
В этом случае выводится приближённый результат
С целью сокращения записи при выводе
могут использоваться подстановки
Содержание
Выход
44

45.

Содержание
Выход
45

46. Решение систем

Также выполняет команда solve
Входные аргументы
левые части уравнений
переменные, по которым нужно разрешить систему
например: s = solve(f1, f2, x1, x2)
Выходной аргумент
структура (запись) s с полями (в данном случае) x1
и x2, хранящими символьное представление
решения
Содержание
Выход
46

47.

Содержание
Выход
47

48. Решение дифференциальных уравнений

Выполняет команда dsolve
Если неизвестная функция обозначена
символьной переменной y, то ее производные
следует обозначать как d[n]y, где в скобках
указан порядок производной.
Содержание
Выход
48