Основы комбинаторного анализа

1.

Основы комбинаторного
анализа
Доцент Федосеева Т.А.

2.

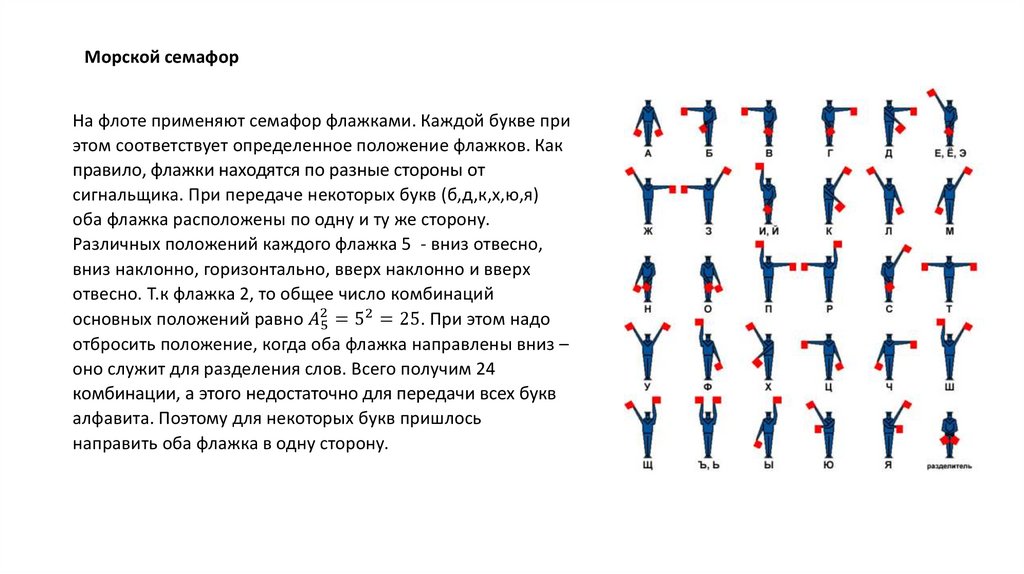
Комбинаторика – это наука о том, как можно комбинировать различные объекты,
как можно их сочетать. Это с одной стороны наука о том, как посчитать количество
комбинаций определенного типа, а с другой стороны наука о том, как найти
комбинацию с какими-то оптимальными свойствами.
Суеверные велосипедисты
Чтобы не иметь проблем с велосипедами, председатель
велосипедистов решил перерегистрировать всех велосипедистов,
исключив из номера билета число 8 (т.к. ему показалось, что
велосипедисты с этим номером имеют проблемы со своим
велосипедом – погнутое колесо, что похоже на цифру 8). Решил он
поменять номера билетов, и выдавать только те номера, где нет
цифры 8. Номера 3х значные, например, номер 000 можно
использовать, а 875 нельзя.
Однозначных номеров, не содержащих 8ку всего 9:
0,1,2,3,4,5,6,7,9
Двузначные номера: из каждого однозначного номера получится
9 двузначных, а т.к. однозначных номеров тоже 9, то получится
9*9=81 двузначный номер без восьмерок.
00, 01, 02, 03, 04, 05, 06, 07, 09
10, 11, 12, 13, 14, 15, 16, 17, 19
20, 21, 22, 23, 24, 25, 26, 27, 29
30, 31, 32, 33, 34, 35, 36, 37, 39
40, 41, 42, 43, 44, 45, 46, 47, 49
50, 51, 52, 53, 54, 55, 56, 57, 59
60, 61, 62, 63, 64, 65, 66, 67, 69
70, 71, 72, 73, 74, 75, 76, 77, 79
80, 81, 82, 83, 84, 85, 86, 87, 89
90, 91, 92, 93, 94, 95, 96, 97, 99

3.

Итак, существует 82=81 двузначный номер без цифры 8. Но за каждым из них снова можно
поставить любую из девяти допустимых цифр. В результате получим 92*9=93=729 трехзначных
номеров. А если взять не 3х значные, а 4х значные номера, то номеров не содержащих 8к
будет 94=6561.
В другом клубе велосипедисты были еще суевернее и отказались от числа 0, т.к. оно похоже
на вытянутое колесо и обходились 8ю цифрами: 1,2,3,4,5,6,7,9. Сколько 3х значных номеров
билетов можно составить?
Ответ: 83=512.
Размещения с повторениями
Тип задач: даны предметы, относящиеся к n различным видам, из них
составляют всевозможные расстановки по k предметов в каждой или kрасстановки. При этом в расстановки могут входить и предметы одного вид, а
две расстановки считаются различными, если они отличаются друг от друга или
видом входящих в них предметов или порядком этих предметов. Надо найти
общее число таких расстановок.
k-размещения с повторениями из элементов n видов: