Похожие презентации:
Число, положение и комбинаторика. Введение в комбинаторику
1. Число, положение и комбинаторика – три взаимно пересекающиеся, но различные сферы мысли, к которым можно отнести все
математические идеи.Джозеф Сильвестр (1844 г.)
ВВЕДЕНИЕ В
КОМБИНАТОРИКУ
2.
3.
4.
Комбинаторика – это разделматематики, посвященный
решению задач на перебор
различных вариантов,
удовлетворяющих каким-либо
правилам или условиям.
5.
Особая приметакомбинаторных задач вопрос,
который начинается
словами:
«Сколькими
способами…?»
6. Особая примета комбинаторных задач - вопрос, который начинается словами: «Сколькими способами…?»
КОМБИНАТОРИКА- это раздел математики, в котором
изучаются простейшие «соединения»:
перестановки, размещения, сочетания.
(Большой Энциклопедический Словарь)
- происходит от латинского слова
«combina», что в переводе на русский
означает – «сочетать», «соединять».
7. КОМБИНАТОРИКА
Несколько стран в качестве символасвоего государства решили использовать
флаг в виде трех горизонтальных полос,
одинаковых по ширине, но разных по цвету:
синий, красный, зеленый. У каждой страны
свой, отличный от других, флаг.
а) Сколько всего стран могут использовать
такую символику?
8.
9.
Несколько стран в качестве символасвоего государства решили использовать
флаг в виде трех горизонтальных полос,
одинаковых по ширине, но разных по цвету:
синий, красный, зеленый. У каждой страны
свой, отличный от других, флаг.
а) Сколько всего стран могут использовать
такую символику?
б) Сколько стран могут использовать
такую символику с верхней зеленой полосой?
10.
11.
12.
СКОЛЬКО РАЗЛИЧНЫХВАРИАНТОВ ЗАВТРАКОВ МОЖНО
СОСТАВИТЬ ИЗ 1 НАПИТКА И 1
ВИДА ВЫПЕЧКИ, ЕСЛИ ВАМ
ПРЕДЛОЖИЛИ: ЧАЙ, КОФЕ,
БУЛОЧКИ, ПЕЧЕНЬЕ И ВАФЛИ?
13. Сколько различных вариантов завтраков можно составить из 1 напитка и 1 вида выпечки, если вам предложили: чай, кофе, булочки,
14.
У Миши 4 ручки разного цвета и 3блокнота разного размера. Сколько
вариантов наборов из ручки и блокнота
сможет составить Миша?
15.
16.
Сколько двузначных чиселможно составить, используя
цифры 1, 2, 3, 4?
а) цифры не могут повторяться;
б) цифры могут повторяться.
А если бы были цифры: 5, 0, 2, 6?
17. Сколько двузначных чисел можно составить, используя цифры 1, 2, 3, 4? а) цифры не могут повторяться; б) цифры могут
Человек, пришедший в гости,забыл код, открывающий дверь
подъезда, но помнил, что он
составлен из нулей и единиц и
содержит четыре цифры.
Сколько вариантов кода ему
придется перебрать, чтобы
открыть дверь?
18.
У КАТИ 2 КОФТЫ И 3 ЮБКИ – ВСЕ РАЗНОГОЦВЕТА. МОЖЕТ ЛИ КАТЯ В ТЕЧЕНИЕ 7
ДНЕЙ НЕДЕЛИ НАДЕВАТЬ КАЖДЫЙ ДЕНЬ
РАЗНЫЕ КОСТЮМЫ?
2 3=6
19. У Кати 2 кофты и 3 юбки – все разного цвета. Может ли Катя в течение 7 дней недели надевать каждый день разные костюмы?
НА ВХОДНОЙ ДВЕРИ ДОМА УСТАНОВЛЕНДОМОФОН, НА ТАБЛО КОТОРОГО
НАНЕСЕНЫ ЦИФРЫ 0,1,2,…9. КАЖДАЯ
КВАРТИРА ПОЛУЧАЕТ КОДОВЫЙ ЗАМОК
ИЗ ДВУХ ЦИФР ТИПА 02, 37 И Т.П. ХВАТИТ
ЛИ КОДОВЫХ ЗАМКОВ ДЛЯ ВСЕХ
КВАРТИР, ЕСЛИ В ДОМЕ 96 КВАРТИР?
(КОД 00 НЕ СУЩЕСТВУЕТ)
10 10 – 1 = 99
20. На входной двери дома установлен домофон, на табло которого нанесены цифры 0,1,2,…9. Каждая квартира получает кодовый замок из
ИЗ ЦИФР: 1, 2, 3, 4, 5 СОСТАВЛЕНЫВСЕВОЗМОЖНЫЕ ТРЕХЗНАЧНЫЕ ЧИСЛА
(ЦИФРЫ МОГУТ ПОВТОРЯТЬСЯ).
КАКИХ ТРЕХЗНАЧНЫХ ЧИСЕЛ БОЛЬШЕ:
СОСТАВЛЕННЫХ ТОЛЬКО ИЗ ЧЕТНЫХ
ИЛИ ТОЛЬКО ИЗ НЕЧЕТНЫХ ЦИФР?
НА СКОЛЬКО?
21. Из цифр: 1, 2, 3, 4, 5 составлены всевозможные трехзначные числа (цифры могут повторяться). Каких трехзначных чисел больше:
НЕЧЕТНЫЕ: 1, 3, 5ЧЕТНЫЕ: 2, 4
3 3 3 – 2 2 2 = 19
22. Нечетные: 1, 3, 5 Четные: 2, 4
КвартетПроказница Мартышка,
Осёл,
Козёл
Да косолапый Мишка
Затеяли сыграть квартет.
…
Стой, братцы, стой! –
Кричит Мартышка, - погодите!
Как музыке идти?
Ведь вы не так сидите…
И так, и этак пересаживались – опять музыка на лад
не идет.
Вот пуще прежнего пошли у них разборы
И споры,
Кому и как сидеть…
Сколькими способами можно рассадить четырех
музыкантов?
4 3 2 1 = 24
23. Квартет Проказница Мартышка, Осёл, Козёл Да косолапый Мишка Затеяли сыграть квартет. … Стой, братцы, стой! – Кричит Мартышка, -
17
13
19
25
31
2
8
14
20
26
32
3
9
15
21
27
33
4
10
16
22
28
34
5
11
17
23
29
35
6
12
18
24
30
36
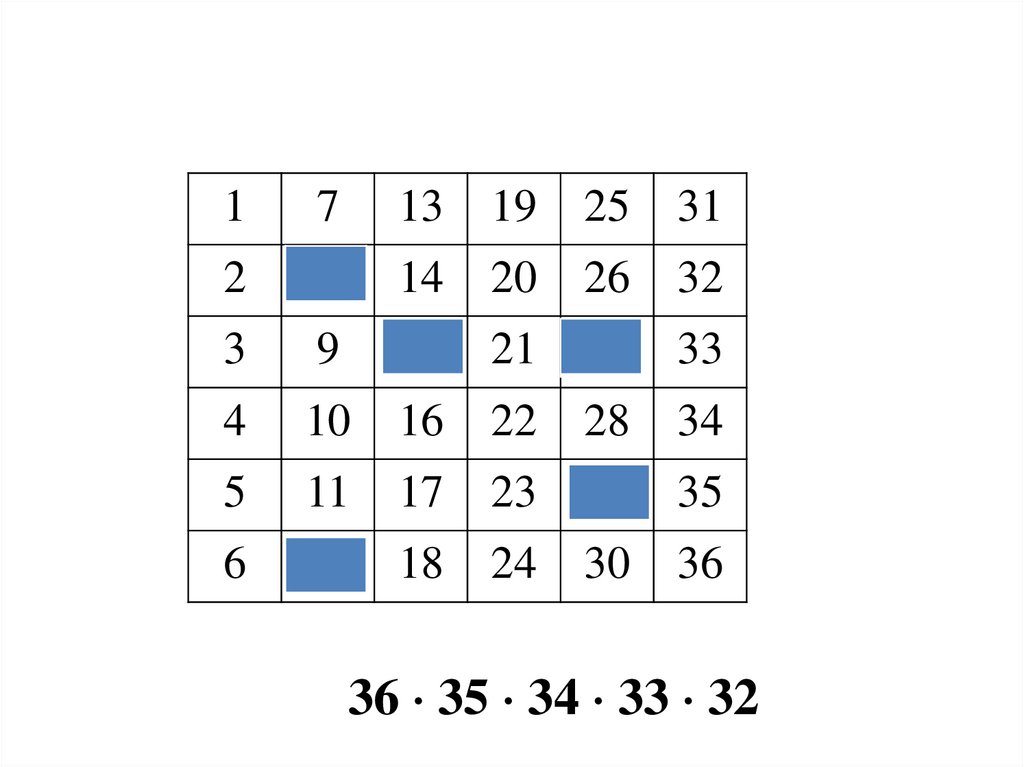
36 35 34 33 32
24.
4523904025. 45239040
ВЫВОДКомбинаторика - раздел математики
который, учит логически мыслить,
перебирая различные варианты решения
комбинаторных задач, повышает
заинтересованность в изучении
математики, учит мыслить нестандартно,
развивает воображение и смекалку.
Применяется во многих сферах
деятельности людей.























 Математика
Математика








