Похожие презентации:
Комбинаторика
1. Комбинаторика
2. Цель урока:
Рассмотреть, что изучаеткомбинаторика, познакомиться
с правилами суммы и
произведения, и научиться их
применять при решении задач.
3. 1. Комбинаторика.
Обычный вопрос в комбинаторныхзадачах: сколькими способами...
К комбинаторным задачам также относятся задачи
построения математических квадратов, задач
расшифровки и кодирования.
Основные правила комбинаторики – это
правила суммы и произведения.
4. Попробуем самостоятельно ответить на ВОПРОСЫ
1. Сколькими способами из 3-ех конфеток можем выбрать одну2. Сколькими способами из 3-ех конфеток можем выбрать две
3. Сколькими способами можем 3-ех человек построить в ряд
4. Сколько диагоналей можно провести в треугольнике
5. Сколько диагоналей можно провести в четырехугольнике
6. Сколько диагоналей можно провести в пятиугольнике
7. Три человека играли в шахматы. Каждый с каждым сыграл
по одному разу. Сколько всего было партий
8. Четыре человека играли в шахматы. Каждый с каждым
сыграл по одному разу. Сколько всего было партий
9. Сколькими способами можно выбрать в нашем классе
старосту и его заместителя
10. Из пункта А в пункт В ведут три дороги, а из В в пункт С две
дороги. Сколькими способами можно добраться из А в С
5.
Рождение комбинаторики как разделаматематики связано с трудами великих
французских математиков 17 века
Пьера Ферма
(1601-1665)
Блеза Паскаля
(1623-1662)
по теории
азартных игр
6. 2. Правило суммы
Запись в тетради:Если некоторый элемент А можно выбрать m
способами, а элемент В - n способами, то выбор
«либо А, либо В» можно сделать m+n способами.
А - m способов;
В - n способов;
А или В - (m+n) способов.
Например: если на тарелке лежат 5 яблок и 6 груш, то
один плод можно выбрать 5+6=11 способами.
Обратите внимание на то, что выбирается не просто
яблоко или груша, а один конкретный плод это
яблоко или эта груша.
7. 3. Правило произведения.
Запись в тетради:Если элемент А можно выбрать m способами, элемент В можно
выбрать n способами, то пару А и В можно выбрать mn
способами.
А — m способов;
В - n способов;
(А и В) - (mn) способов.
Например:
если есть 2 разных конверта, 3 разные марки, то выбрать то
выбрать конверт и марку можно 2*3=6 способами. Обратите
внимание - выбирается пара конверт и марка. Правило
произведения верно и в том случае, когда рассматриваются
элементы нескольких множеств.
Например:
если есть 2 разных конверта и 3 разные марки и 4 разные
открытки, то выбрать конверт, марку и открытку можно
2*3*4=24 способами.
8.
9. Задача 1
Сколько существует вариантов покупки однойрозы,
если продают 3 алые,
2 белые и 4 желтые
розы?
10. Решение:
Выбирается 1 роза. Правило суммы 3+2+4=9(способов).
11. ЗАДАЧА 2.
В столовой есть 4 первых блюда и 7 вторых.Сколько различных вариантов обеда из 2
блюд можно заказать?
12. Решение:
Выбирается 2 блюда. Правилопроизведения 4.7=28 (вариантов).
13. Задача 3.
На блюде лежат 7 яблок 3 груши и 4 апельсинаа) сколькими способами можно взять с блюда 1 плод;
б) сколькими способами можно взять: (яблоко с
грушей); (яблоко с апельсином); (грушу с апельсином);
в) сколькими способами можно взять 2 фрукта с
разными названиями.
14. Решение:
а) выбирается 1 плод. Правило суммы7+3+4=14;
б) выбирается 2 плода. Правило
произведения: (7.3=21 способ ), (7.4=28
способов ), (3.4=12 способов );
в) применяются оба правила. Сначала правило произведения (выбирается пара) и
затем – правило суммы (эта пара
рассматривается как единое целое)
7.3+7.4+3.4=21+28+12=61 (способ ).
15. Задача 4.
Сколько различных двузначных чиселможно составить , используя цифры 1,
4 и 7, если цифры могут повторяться?
16. Решение:
1-й способ (перебор)11 41 71
14 44 74
17 47 77
Ответ: 9 чисел.
2-й способ (использование формулы)
- двузначное число. Способ
записи числа 3.3=9
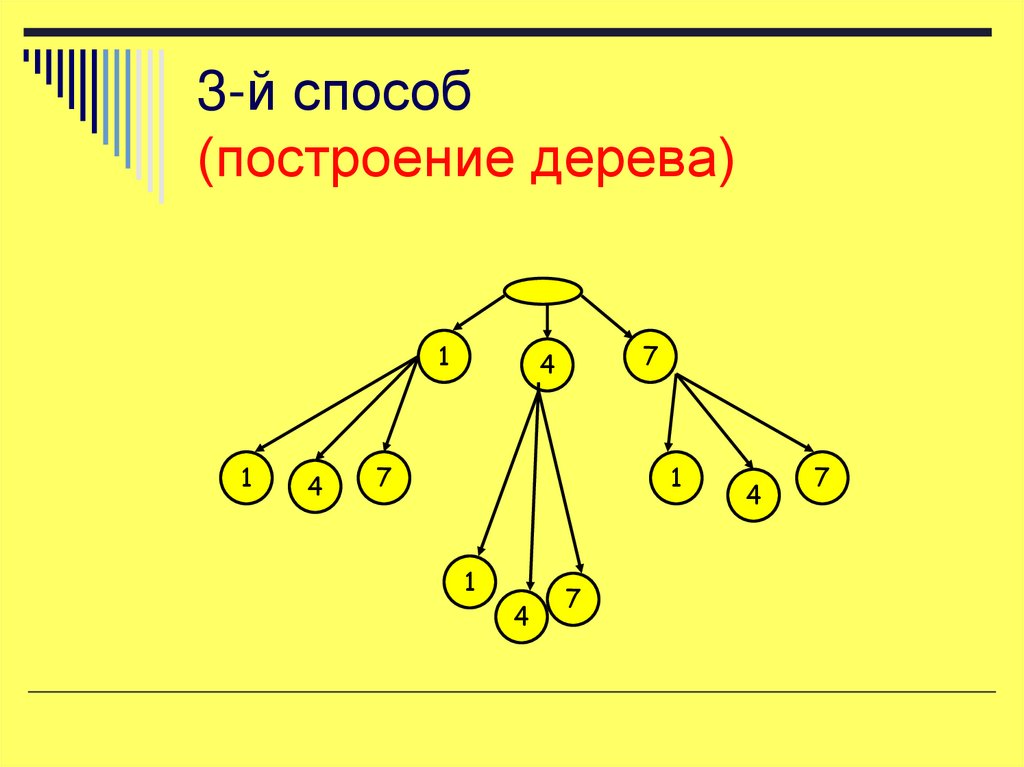
17. 3-й способ (построение дерева)
11
4
7
4
7
1
1
4
7
4
7
18. Задача 5.
В пакете драже лежат 9 красных,10 синих и 12зелёных конфет.
а) сколькими способами можно взять 1 конфету?
б) сколькими способами можно взять:
красную и синюю конфеты;
красную и зеленую конфеты;
синюю и зеленую конфеты.
в) сколькими способами взять 2 конфеты разного
цвета.
19. Решение:
а) 9+10+12=31(способ)• б)
1) 9.10=90(способов),
2) 9.12=108 (способов),
3)10.12=120(способов)
в)9.10+9.12+10.12=318(способов)
20. Задача 6
Сколько различных трехзначныхчисел можно составить , используя
цифры 3 и 5,если цифры могут
повторяться?
21. Решение:
1-й способ (перебор)333 555
335 553
355 533
353 535
(8 чисел)
2-й способ (формула)
2.2.2=8 (чисел)
22. Задача 7
Сколько различных флагов можносшить из материи 3-х цветов :
красного, синего и белого, если
каждый должен состоять из 3-х
равных горизонтальных полос разного
цвета?
23. Решение
Вариантов решения этой задачи немного, ихможно последовательно перебрать.
К К С С
С Б Б К
Б С К Б
Б Б
С К
К С
Есть ли среди них флаг
России?
24. Задача 8.
От Кащея до Бабы-Яги ведут 3 дороги, а отБабы-Яги до Кикиморы 2 дороги. Сколькими
способами можно пройти от Кащея до
Кикиморы, заходя к Бабе-Яге?
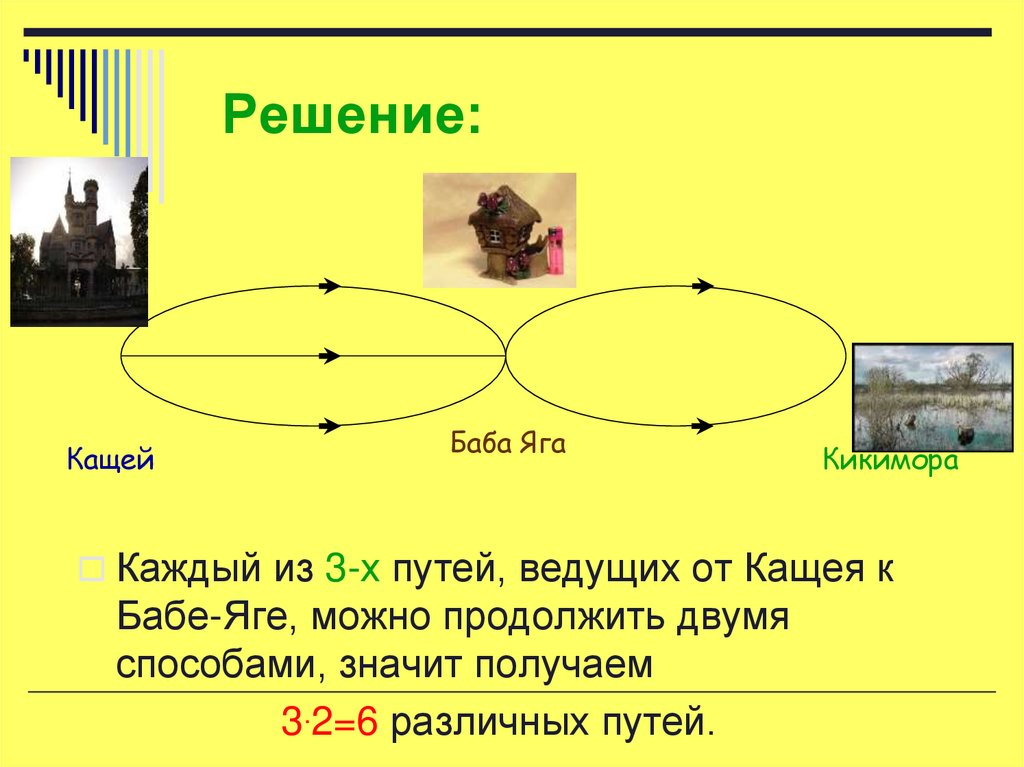
25. Решение:
КащейБаба Яга
Кикимора
Каждый из 3-х путей, ведущих от Кащея к
Бабе-Яге, можно продолжить двумя
способами, значит получаем
3.2=6 различных путей.
26. Задача 9.
В корзине сидят котята - 2 черных, 2 рыжих и1 полосатый. Сколькими способами можно
выбрать трех котят так, чтобы они все были
разной окраски?
27. Решение:
По условию, полосатого котенка надовыбирать всегда, то есть способ выбора
всего один.
Черного котенка можно выбрать двумя
способами; рыжего – тоже двумя
Всего получаем:
1.2.2=4 способа.
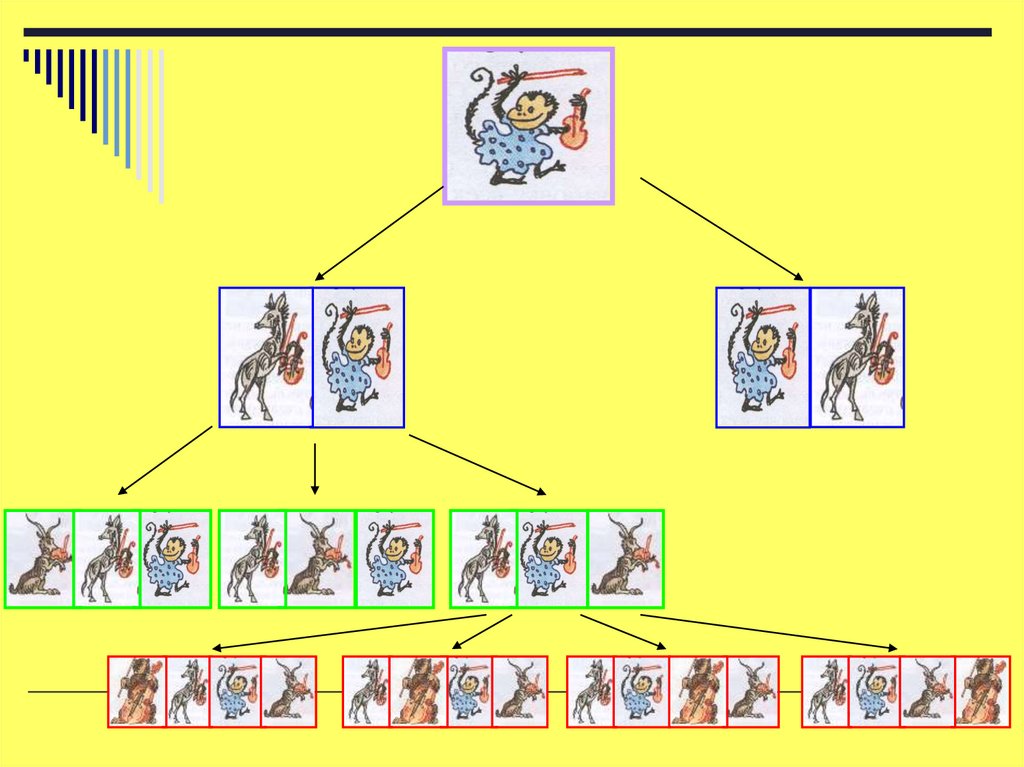
28. Задача 10.
«ПроказницаМартышка, Осел,
Козел да косолапый
Мишка задумали
сыграть квартет ….»
Сколькими способами они могут пересесть?
29.
30. Подводим итоги.
Оцените степеньвашего усвоения
материала:
а) усвоил полностью,
могу применить;
б) усвоил полностью,
но затрудняюсь в
применении;
в) не усвоил.


























 Математика
Математика








