Похожие презентации:
Случайные величины (СВ). Дискретные случайные величины (ДСВ)
1.
x1n2Случайные величины (СВ)
Случайной называют величину, принимающую в результате
опыта единственное значение, заранее неизвестное и зависящее от
случайных причин.
СВ обычно обозначаются заглавными латинскими буквами с конца
алфавита X, Y, Z, а их значения – строчными буквами x1, x2, x3,…
y1, y2, y3,…
Дискретной называется такая случайная величина, которая
принимает значения, изолированные друг от друга.
Случайная величина называется непрерывной, если она
может принимать все значения из некоторого конечного или
бесконечного промежутка.
2.
Дискретные случайные величины (ДСВ)Закон распределения
Законом распределения СВ называют соотношение между
возможными значениями случайной величины и их вероятностями.
Пусть X – дискретная случайная величина, которая может
принимать значения х1, х2,…, хn с вероятностями р1, р2,…, рn, соответственно.
n
n
i 1
i 1
p( X xi ) pi 1
– условие нормировки для дискретной СВ.
3.
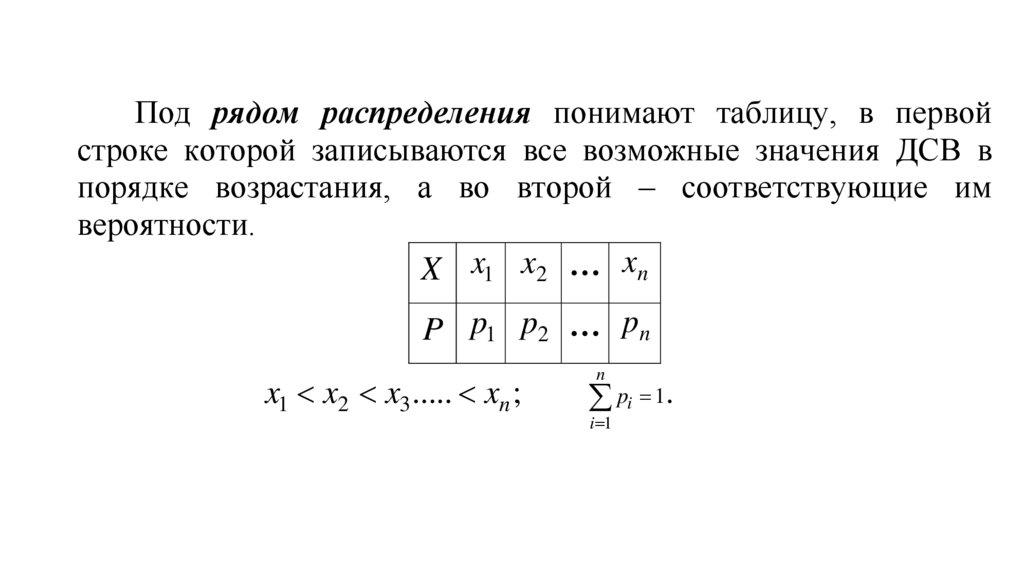
Под рядом распределения понимают таблицу, в первойстроке которой записываются все возможные значения ДСВ в
порядке возрастания, а во второй – соответствующие им
вероятности.
X x1 x2 … xn
P p1 p2 … pn
x1 x2 x3 ..... xn ;
n
pi 1.
i 1
4.
Пример. Вероятность попадания в мишень для первогострелка равна 0,9, для второго – 0,8. Составить закон распределения
для ДСВ Х – числа попаданий в мишень, если каждый стрелок
стреляет по одному разу.
Введем события: Аi –в мишень попал i-й стрелок (i=1,2), Bk –
_
число попаданий в мишень, k 0,2 . B0 A1 A2
_
P( B0 ) P( A1 ) P( A2 ) 0,1 0,2 0,02.
5.
__
B1 A1 A2 A2 A1
P( X 1 ) P( B1 ) P( A1 A2 A1 A2 ) 0,9 0,2 0,1 0,8 0,26
P( X 2 ) P( B2 ) P( A1 A2 ) P( A1 )P( A2 ) 0,9 0,8 0,72
X
0
1
2
P
0,02 0,26 0,72
Проверка: 0,02+0,26+0,72=1.
6.
Функция распределения случайной величиныФункцией распределения случайной величины называется функция F(x),
которая для любого действительного числа х равна вероятности того, что
СВ примет значение, меньшее значения аргумента функции
F( x ) P( X x )
Если представить случайную величину как случайную точку, принимающую
некоторые значения на числовой оси, то функция распределения равна
вероятности того, что случайная точка окажется левее точки х, т. е. попадет в
интервал ( ,x
. )
F(x) применима как для дискретных, так и для непрерывных случайных
величин.
7.
Пример. Составить функцию распределения F(x) для СВ X,заданной рядом распределения:
Х
2
3
4
Р
0,2
0,3
0,5
Пусть аргумент функции x 2. Так как по условию СВ не
может принимать значения, меньшие двух, то F(x)=0. Отдельно
найдем F(2). Согласно определению функции распределения
F ( 2 ) P( X < 2 ) 0.
















































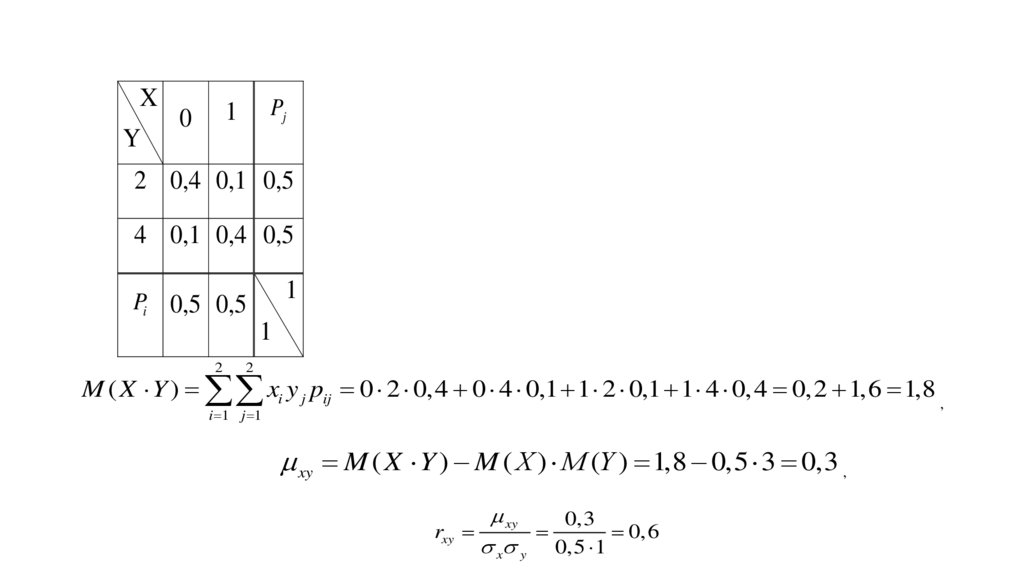
 Математика
Математика








