Сети Петри: эквивалентные формы задания, свойства сетей. Практическое занятие 4

1.

Сети Петри:
эквивалентные формы задания,
свойства сетей
Практическое занятие 4
Дисциплина: Моделирование
технических систем

2.

Сети Петри: эквивалентные формы задания,
свойства сетей
2
Сети Петри разработаны для описания и моделирования
систем, состоящих из отдельных взаимодействующих
блоков. При этом допускается описание одновременно
функционирующих блоков. Каждый блок может быть
рассмотрен как отдельная подсистема, и его поведение
можно описать независимо от других блоков, сохраняя
взаимодействие с ними.
Сети Петри являются эффективным инструментом
моделирования дискретно протекающих процессов с
возможностью отображения параллелизма и асинхронности
процессов, а также иерархичности моделируемых объектов.

3.

Сети Петри: эквивалентные формы задания,
свойства сетей
3
Сеть Петри формально представляется как набор вида
N=(P,T,F,H,μ0),
где Р = {р1, р2, ..., рn} – конечное непустое множество позиций
(n > 0);
T = {t1, t2, ..., tm} – конечное непустое множество переходов
(m ≥ 0);
F: Р Т→{0,1,2,…} – входная функция-отображение позиций в
комплекты переходов;
H: Т Р→{0,1,2,…} – выходная функция-отображение
переходов в комплекты позиций;
μ0 = {0,1,2,…} начальная маркировка(разметка) сети.
Изображение сети в виде графа является наглядной
формой связей позиций и переходов сети Петри. На практике
более удобной может оказаться одна их эквивалентных форм.

4.

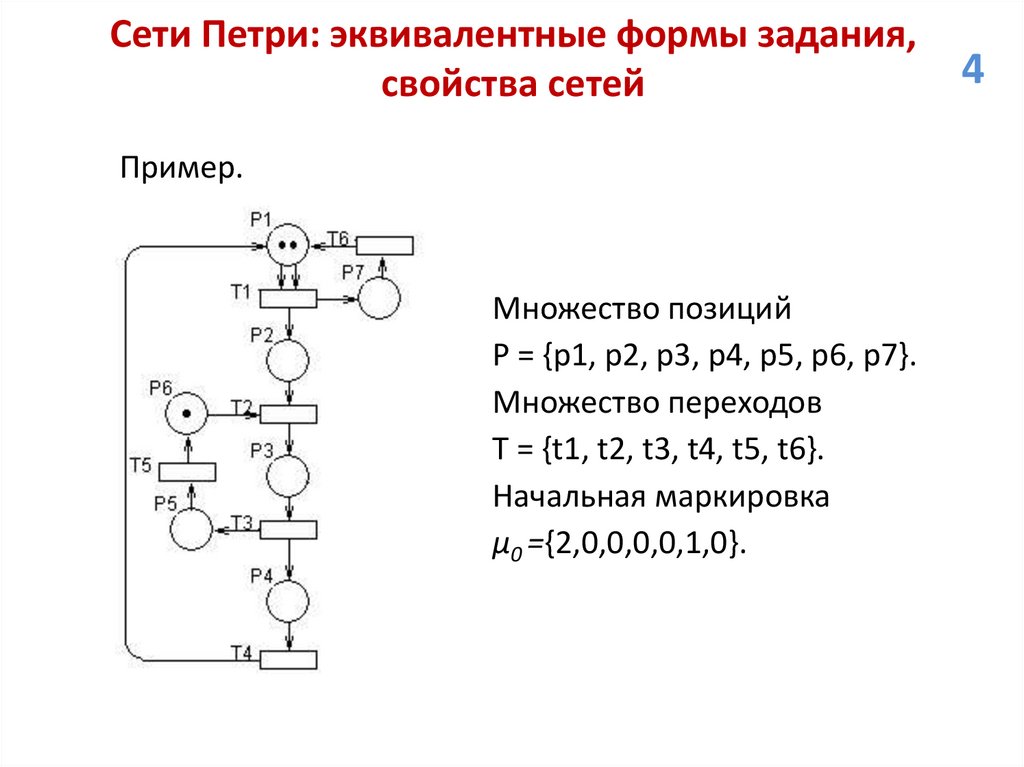
Сети Петри: эквивалентные формы задания,
свойства сетей
Пример.
Множество позиций
Р = {р1, р2, р3, р4, р5, р6, р7}.
Множество переходов
T = {t1, t2, t3, t4, t5, t6}.
Начальная маркировка
μ0 ={2,0,0,0,0,1,0}.
4

5.

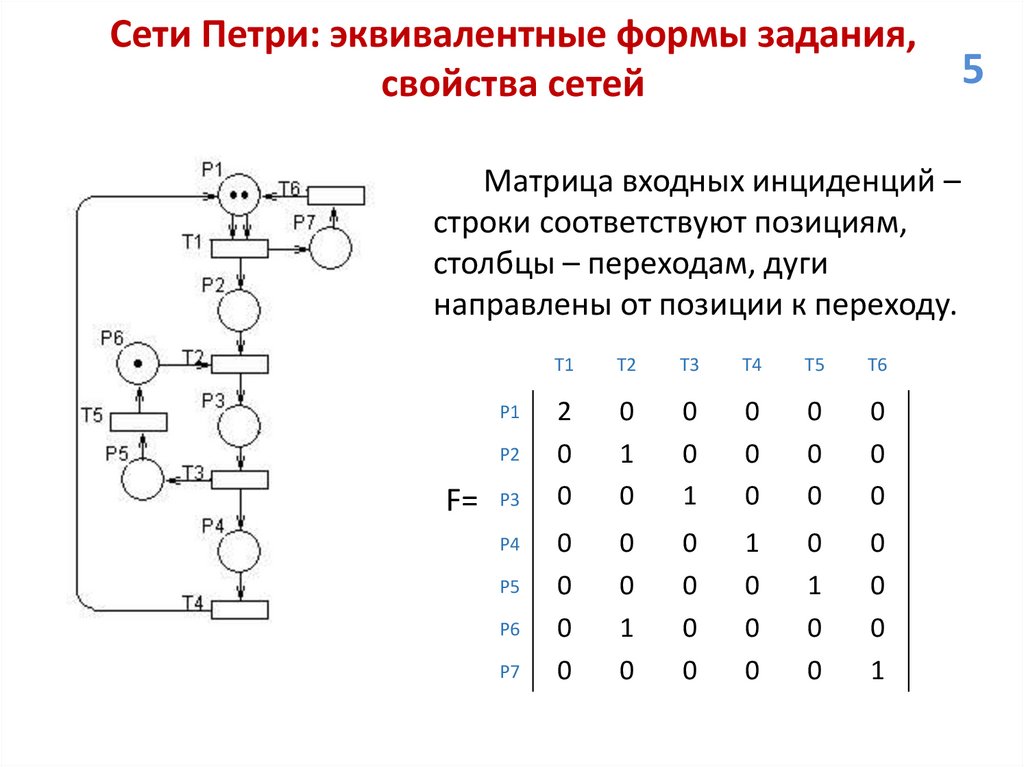
Сети Петри: эквивалентные формы задания,
свойства сетей
Матрица входных инциденций –
строки соответствуют позициям,
столбцы – переходам, дуги
направлены от позиции к переходу.
Р1
Р2
F= Р3
Р4
Р5
Р6
Р7
Т1
Т2
Т3
Т4
Т5
Т6
2
0
0
0
1
0
0
0
1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
1
0
0
0
0
0
1
0
0
0
0
1
0
0
0
0
0
1
5

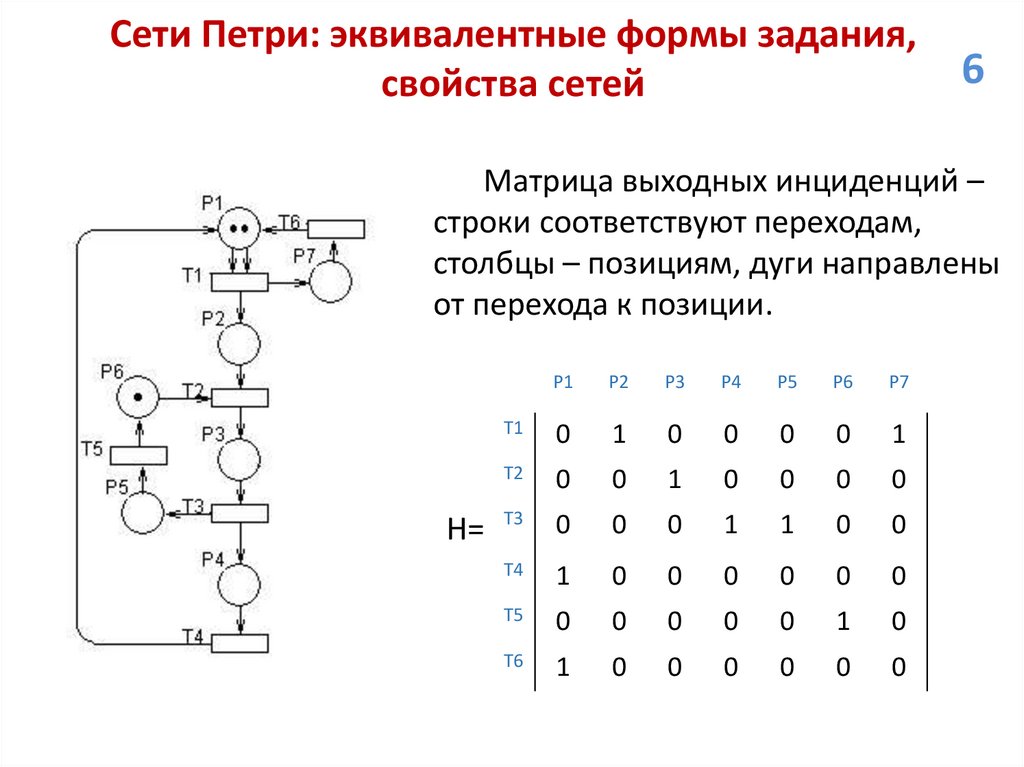
6.

Сети Петри: эквивалентные формы задания,
свойства сетей
6
Матрица выходных инциденций –
строки соответствуют переходам,
столбцы – позициям, дуги направлены
от перехода к позиции.
Р1
Р2
Р3
Р4
Р5
Р6
Р7
Т1
0
1
0
0
0
0
1
Т2
0
0
1
0
0
0
0
H= Т3 0
0
0
1
1
0
0
Т4
1
0
0
0
0
0
0
Т5
0
0
0
0
0
1
0
Т6
1
0
0
0
0
0
0

7.

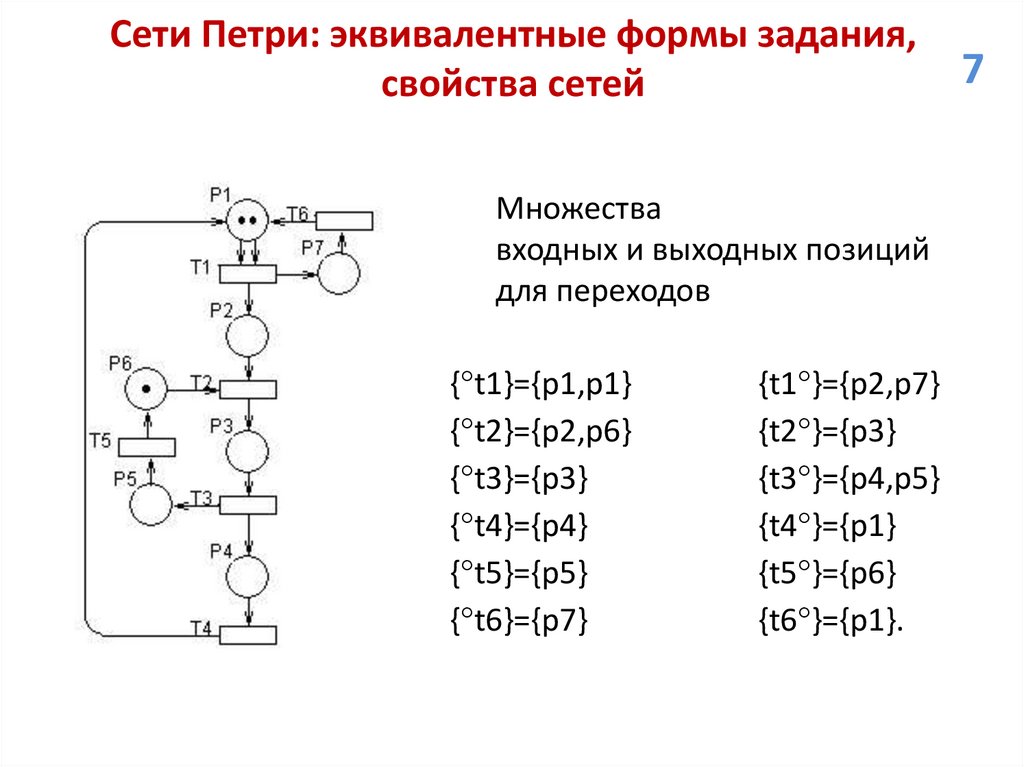
Сети Петри: эквивалентные формы задания,
свойства сетей
Множества
входных и выходных позиций
для переходов
{ t1}={p1,p1}
{ t2}={p2,p6}
{ t3}={p3}
{ t4}={p4}
{ t5}={p5}
{ t6}={p7}
{t1 }={p2,p7}
{t2 }={p3}
{t3 }={p4,p5}
{t4 }={p1}
{t5 }={p6}
{t6 }={p1}.
7

8.

Сети Петри: эквивалентные формы задания,
свойства сетей Т1 Т2 Т3 Т4 Т5 Т68
Множество
входных позиций
для переходов
сопоставляют со
столбцами
матрицы выходных
инциденций
Множество
выходных позиций
для переходов
сопоставляют со
строками матрицы
выходных
инциденций
2
0
0
0
1
0
0
0
1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
1
0
0
0
0
0
1
0
0
0
0
1
0
0
0
0
0
1
Р1
Р2
Р3
Р4
Р5
Р6
Р7
Т1
0
1
0
0
0
0
1
Т2
0
0
1
0
0
0
0
H= Т3 0
0
0
1
1
0
0
Т4
1
0
0
0
0
0
0
Т5
0
0
0
0
0
1
0
Т6
1
0
0
0
0
0
0
Р1
{ t1}={p1,p1}
{ t2}={p2,p6}
{ t3}={p3}
{ t4}={p4}
{ t5}={p5}
{ t6}={p7}
{t1 }={p2,p7}
{t2 }={p3}
{t3 }={p4,p5}
{t4 }={p1}
{t5 }={p6}
{t6 }={p1}
Р2
F= Р3
Р4
Р5
Р6
Р7

9.

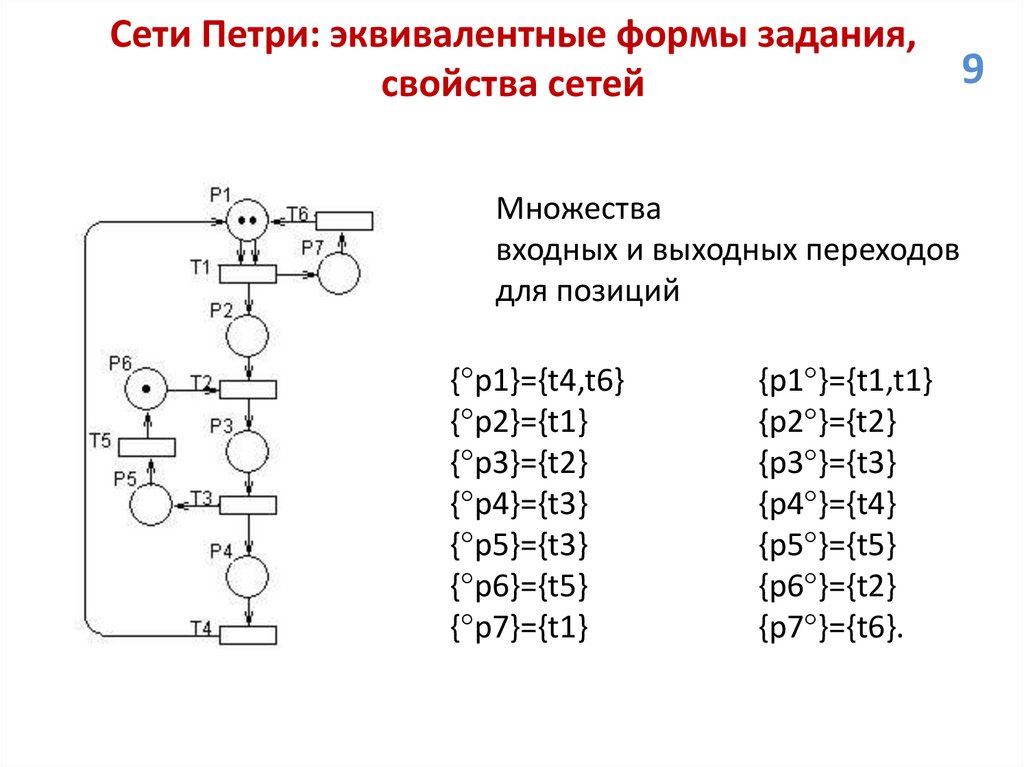
Сети Петри: эквивалентные формы задания,
свойства сетей
Множества
входных и выходных переходов
для позиций
{ p1}={t4,t6}
{ p2}={t1}
{ p3}={t2}
{ p4}={t3}
{ p5}={t3}
{ p6}={t5}
{ p7}={t1}
{p1 }={t1,t1}
{p2 }={t2}
{p3 }={t3}
{p4 }={t4}
{p5 }={t5}
{p6 }={t2}
{p7 }={t6}.
9

10.

Сети Петри: эквивалентные формы задания,
10
свойства сетей
Множество
входных переходов
для позиций
сопоставляют со
столбцами
матрицы выходных
инциденций
Множество
выходных переходов
для позиций
сопоставляют со
строками матрицы
входных инциденций
Т1
{ p1}={t4,t6}
Т2
{ p2}={t1}
{ p3}={t2} H= Т3
{ p4}={t3}
Т4
{ p5}={t3}
Т5
{ p6}={t5}
Т6
{ p7}={t1}.
{p1 }={t1,t1}
{p2 }={t2}
{p3 }={t3}
{p4 }={t4}
{p5 }={t5}
{p6 }={t2}
{p7 }={t6}.
Р1
Р2
F= Р3
Р4
Р5
Р6
Р7
Р1
Р2
Р3
Р4
Р5
Р6
Р7
0
1
0
0
0
0
1
0
0
1
0
0
0
0
0
0
0
1
1
0
0
1
0
0
0
0
0
0
0
0
0
0
0
1
0
1
0
0
0
0
0
0
Т1
Т2
Т3
Т4
Т5
Т6
2
0
0
0
1
0
0
0
1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
1
0
0
0
0
0
1
0
0
0
0
1
0
0
0
0
0
1

11.

Сети Петри: эквивалентные формы задания,
11
свойства сетей
Переход запускается удалением маркеров из его входных
позиций и добавлением маркеров в выходные позиции
перехода. В общем случае запуск перехода tj заменяет
маркировку сети Петри µ на новую маркировку µ',
определяемую соотношением
µ'(рi) = µ(рi) – F(рi,tj) + H(рi,tj).
Таким образом, функционирование сети Петри отображается
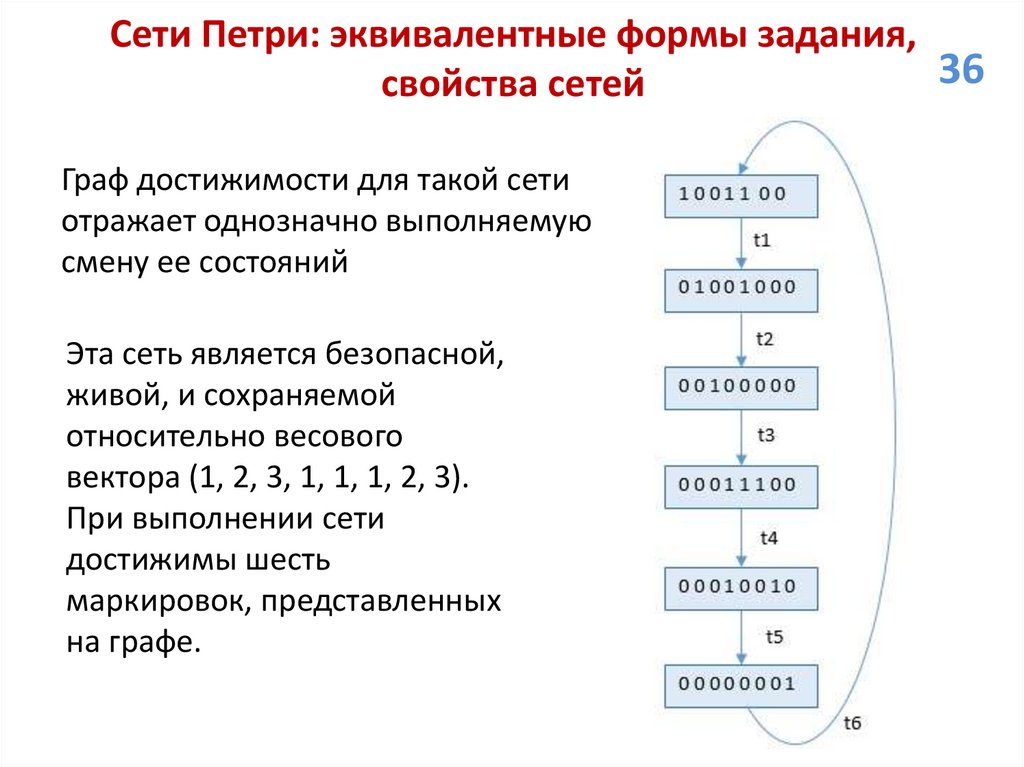
сменой ее маркировки. Анализ функционирования сети
выполняется с помощью дерева достижимости. Граф
достижимости – это граф вершинами которого являются
достижимые маркировки, в корневой вершине размещают
маркировку µ0. Если из некоторой вершины µ1 в другую
вершину µ2 ведет дуга, то она помечается переходом tj T,
переводящим сеть Петри из маркировки µ1 в µ2.

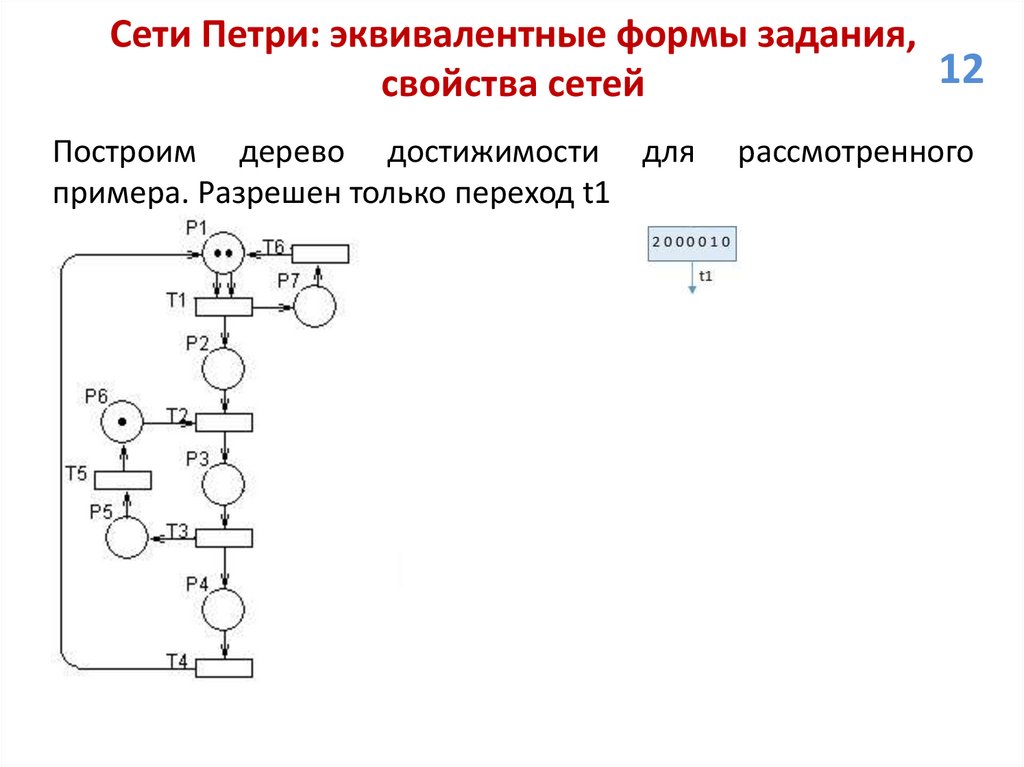
12.

Сети Петри: эквивалентные формы задания,
12
свойства сетей
Построим дерево достижимости для
примера. Разрешен только переход t1
рассмотренного

13.

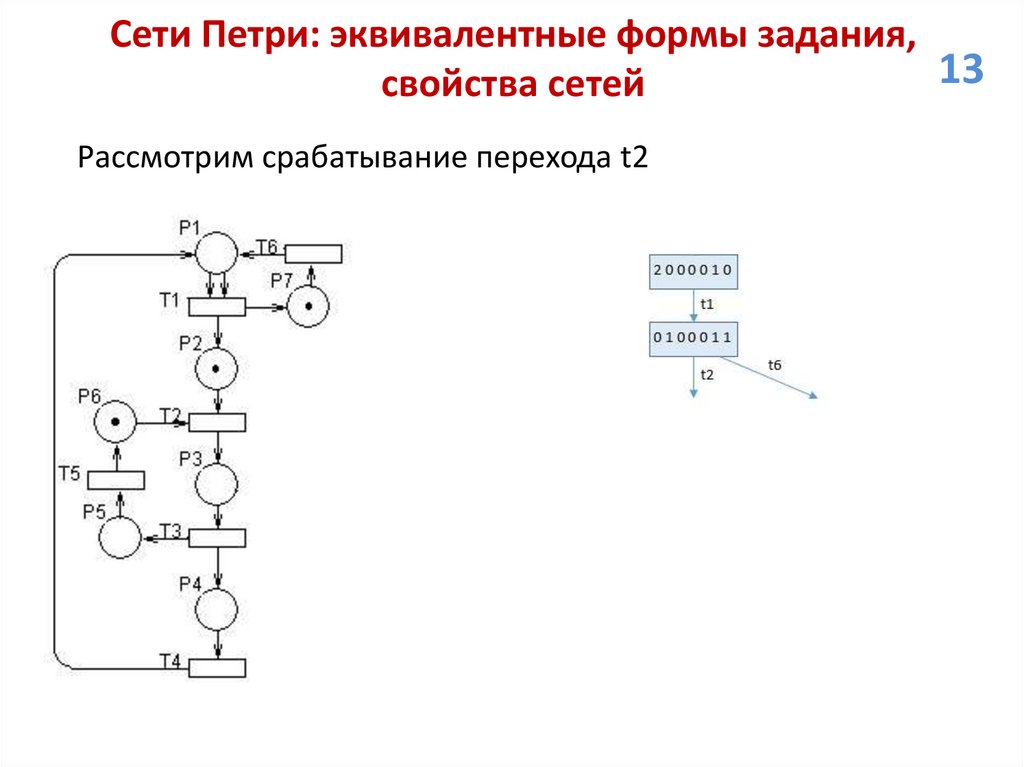
Сети Петри: эквивалентные формы задания,
13
свойства сетей
Рассмотрим срабатывание перехода t2

14.

Сети Петри: эквивалентные формы задания,
14
свойства сетей
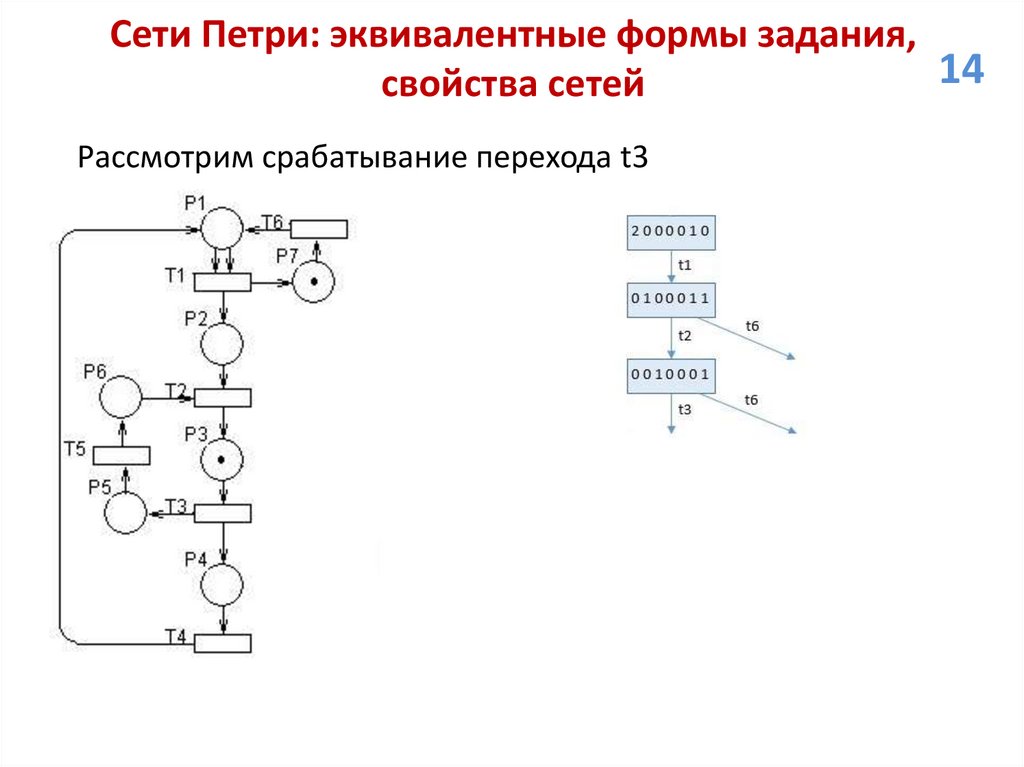
Рассмотрим срабатывание перехода t3

15.

Сети Петри: эквивалентные формы задания,
15
свойства сетей
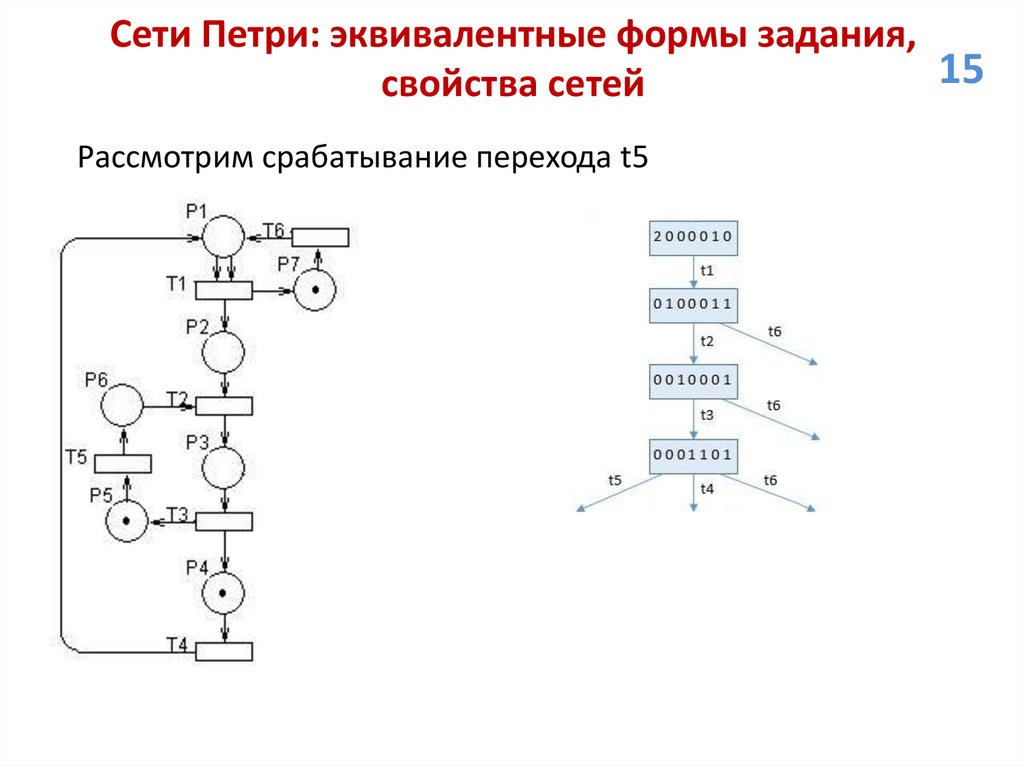
Рассмотрим срабатывание перехода t5

16.

Сети Петри: эквивалентные формы задания,
16
свойства сетей
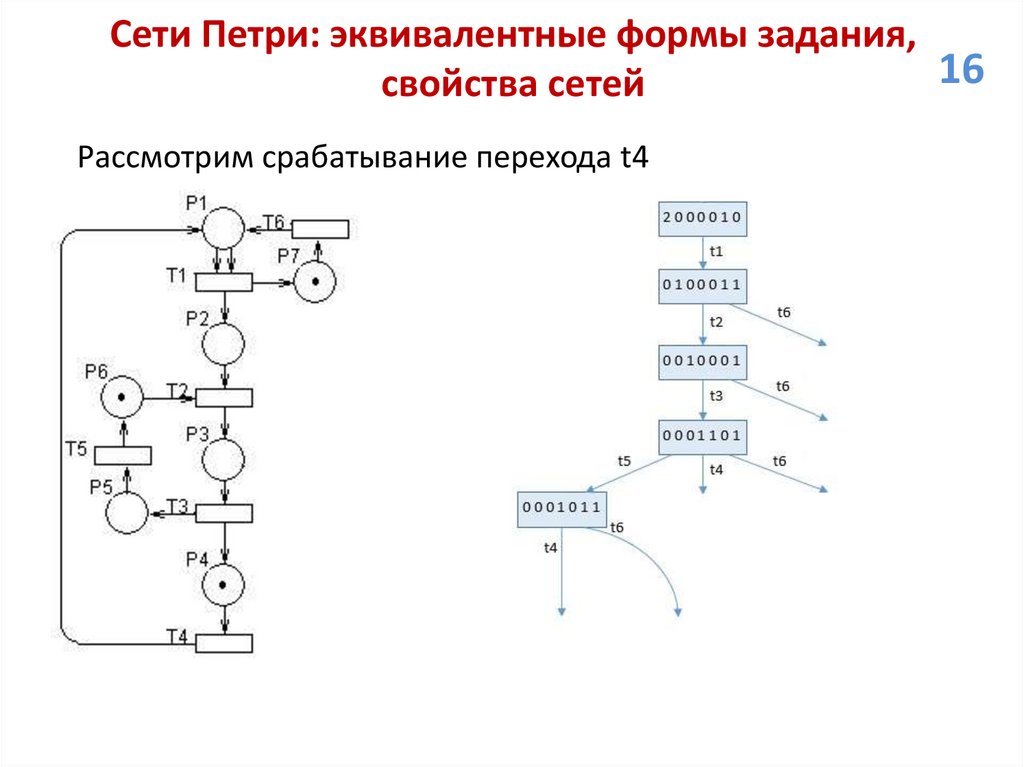
Рассмотрим срабатывание перехода t4

17.

Сети Петри: эквивалентные формы задания,
17
свойства сетей
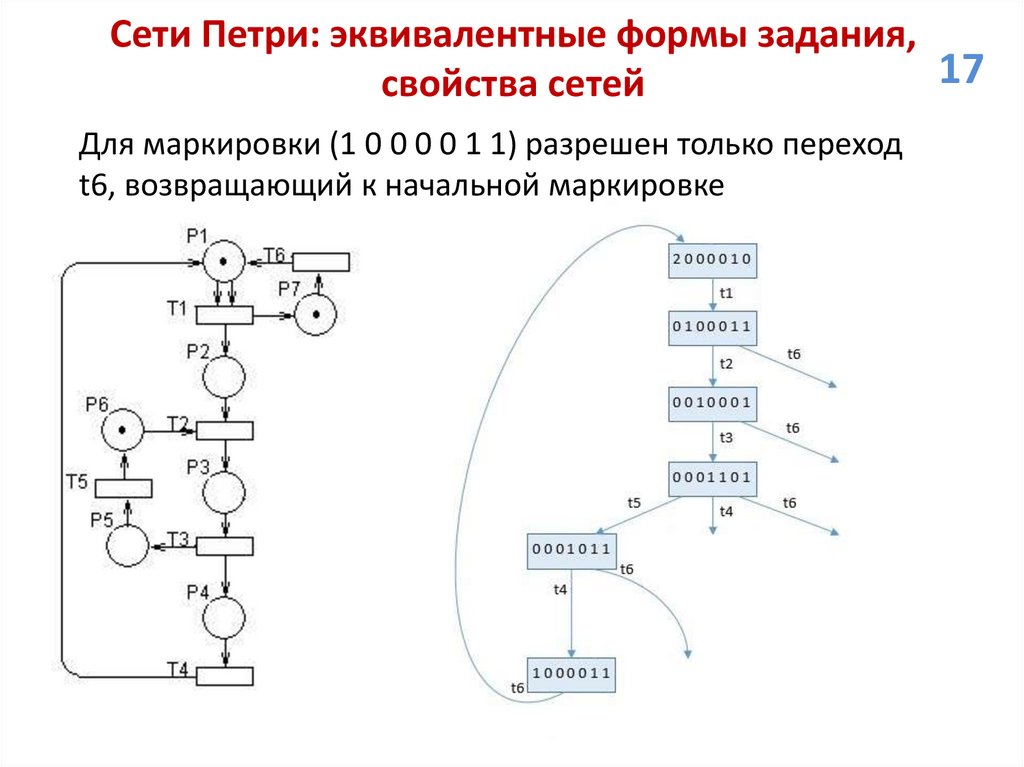
Для маркировки (1 0 0 0 0 1 1) разрешен только переход
t6, возвращающий к начальной маркировке

18.

Сети Петри: эквивалентные формы задания,
18
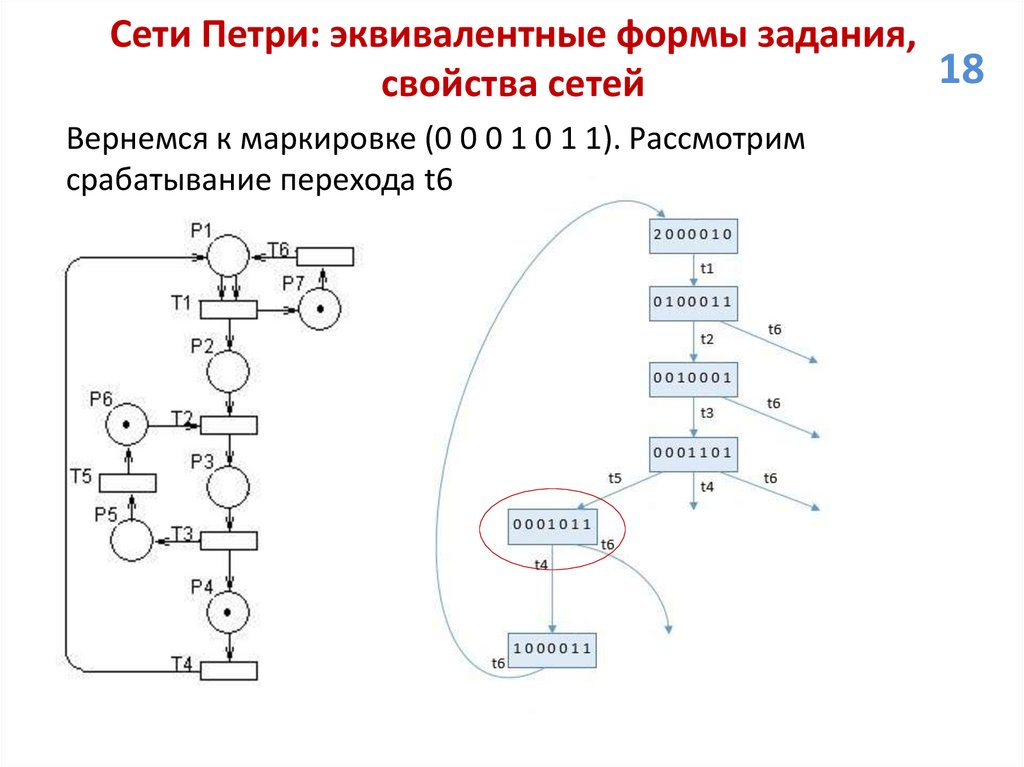
свойства сетей
Вернемся к маркировке (0 0 0 1 0 1 1). Рассмотрим
срабатывание перехода t6

19.

Сети Петри: эквивалентные формы задания,
19
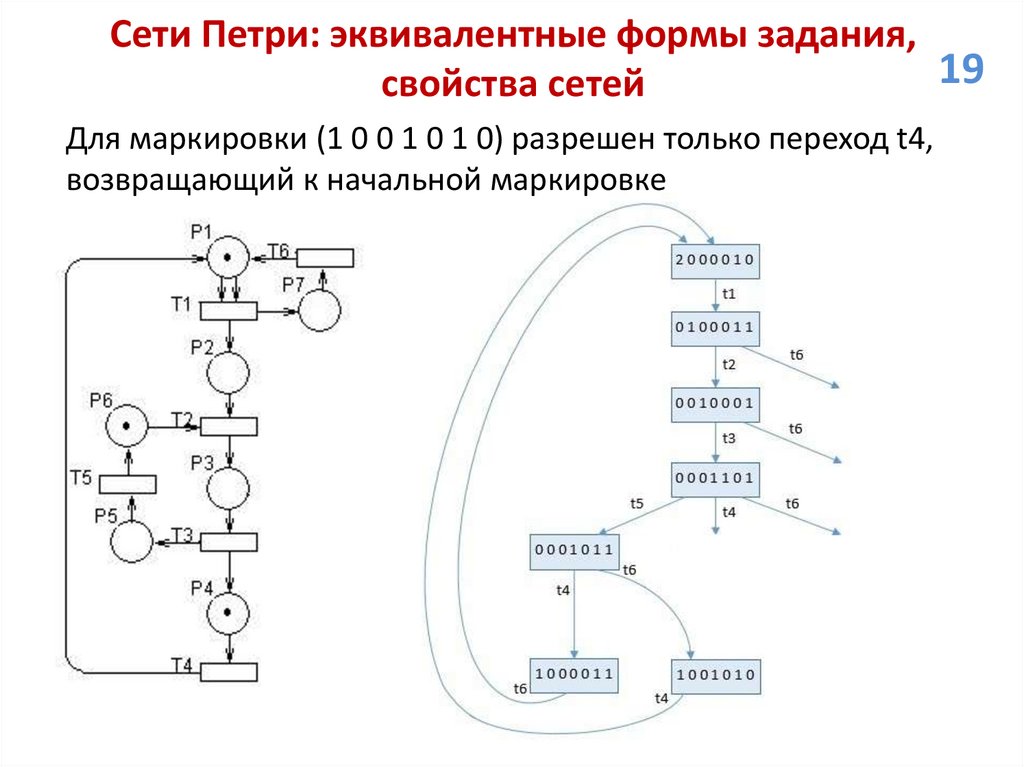
свойства сетей
Для маркировки (1 0 0 1 0 1 0) разрешен только переход t4,
возвращающий к начальной маркировке

20.

Сети Петри: эквивалентные формы задания,
20
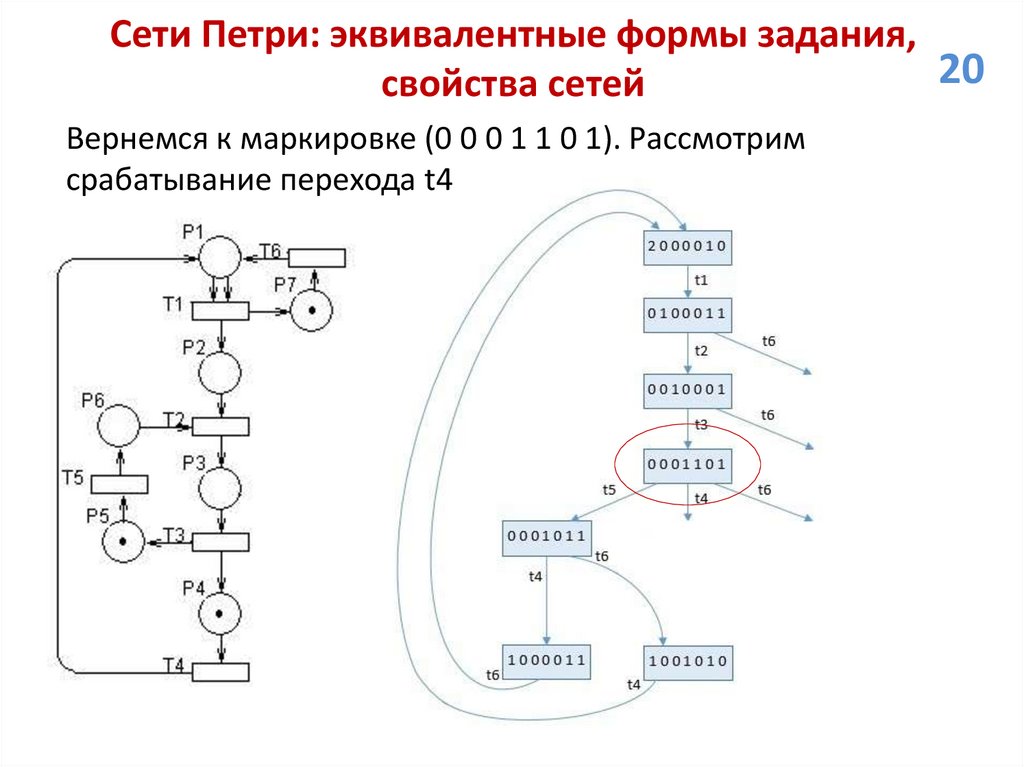
свойства сетей
Вернемся к маркировке (0 0 0 1 1 0 1). Рассмотрим
срабатывание перехода t4

21.

Сети Петри: эквивалентные формы задания,
21
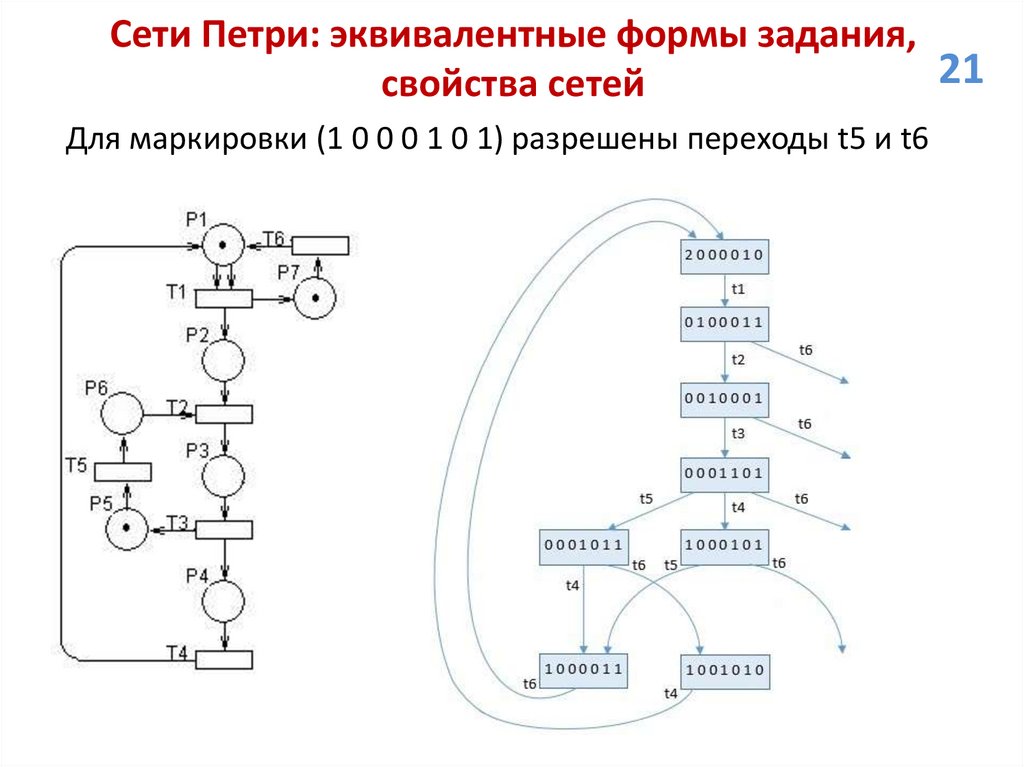
свойства сетей
Для маркировки (1 0 0 0 1 0 1) разрешены переходы t5 и t6

22.

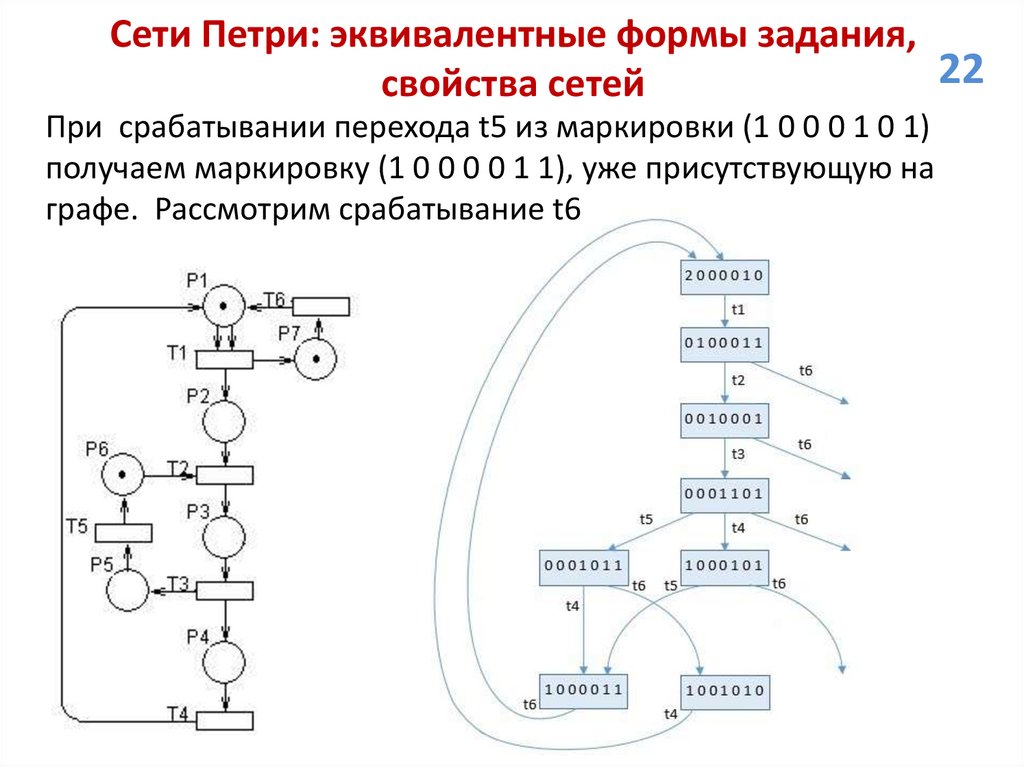
Сети Петри: эквивалентные формы задания,
22
свойства сетей
При срабатывании перехода t5 из маркировки (1 0 0 0 1 0 1)
получаем маркировку (1 0 0 0 0 1 1), уже присутствующую на
графе. Рассмотрим срабатывание t6

23.

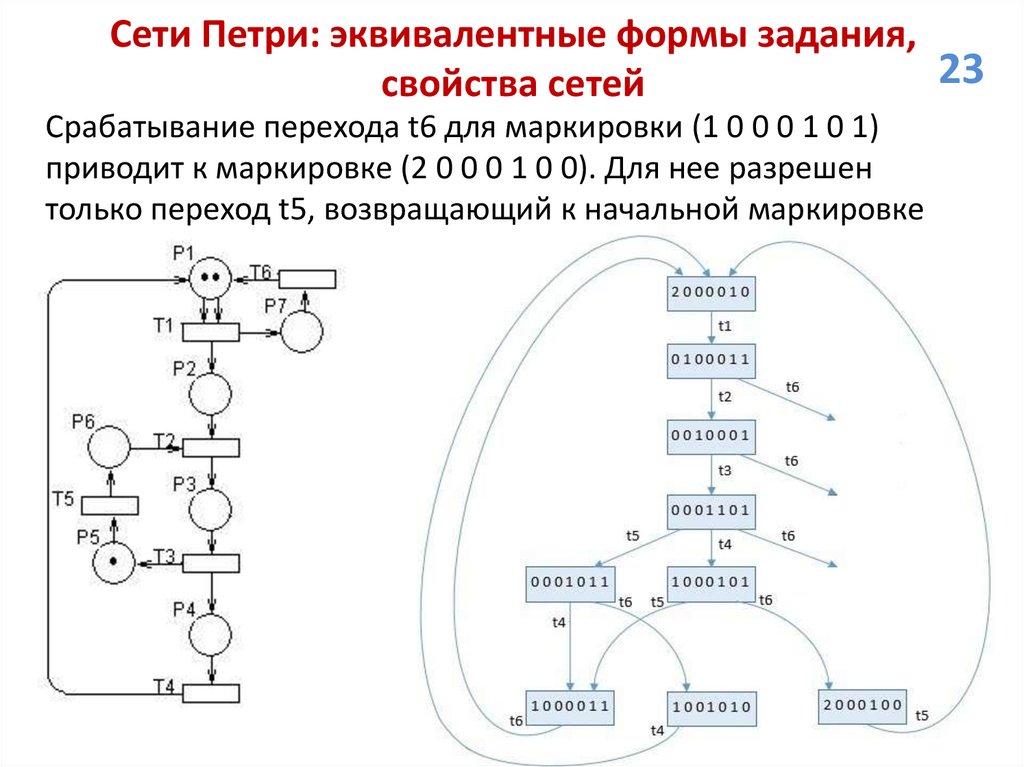
Сети Петри: эквивалентные формы задания,
23
свойства сетей
Срабатывание перехода t6 для маркировки (1 0 0 0 1 0 1)
приводит к маркировке (2 0 0 0 1 0 0). Для нее разрешен
только переход t5, возвращающий к начальной маркировке

24.

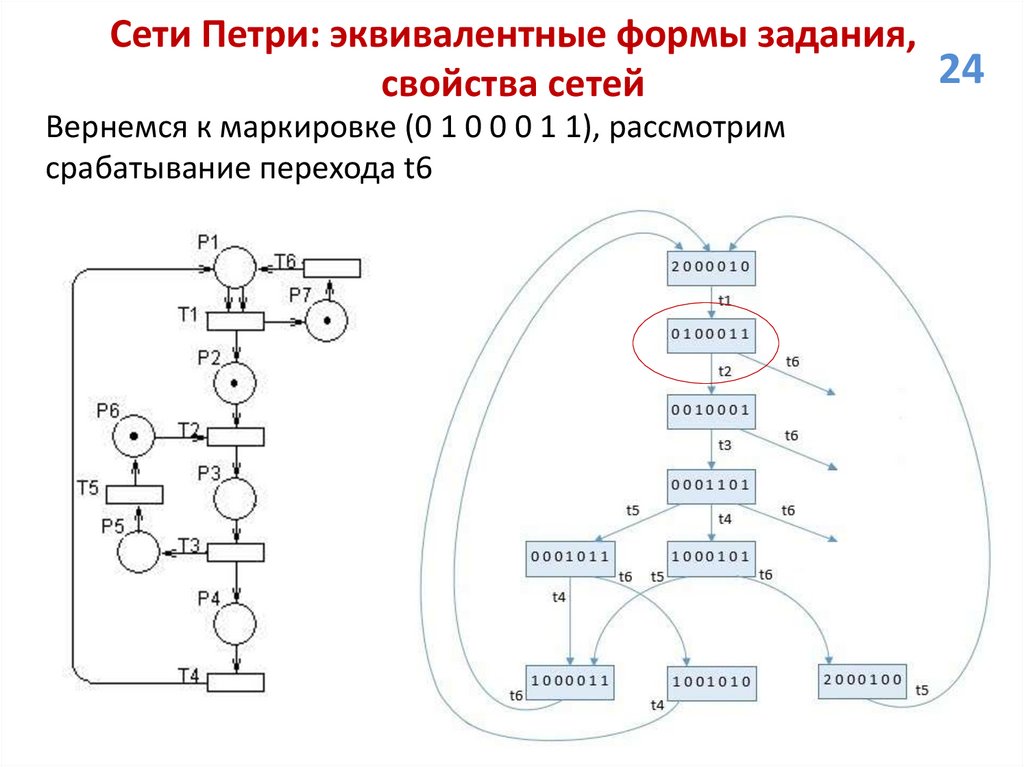
Сети Петри: эквивалентные формы задания,
24
свойства сетей
Вернемся к маркировке (0 1 0 0 0 1 1), рассмотрим
срабатывание перехода t6

25.

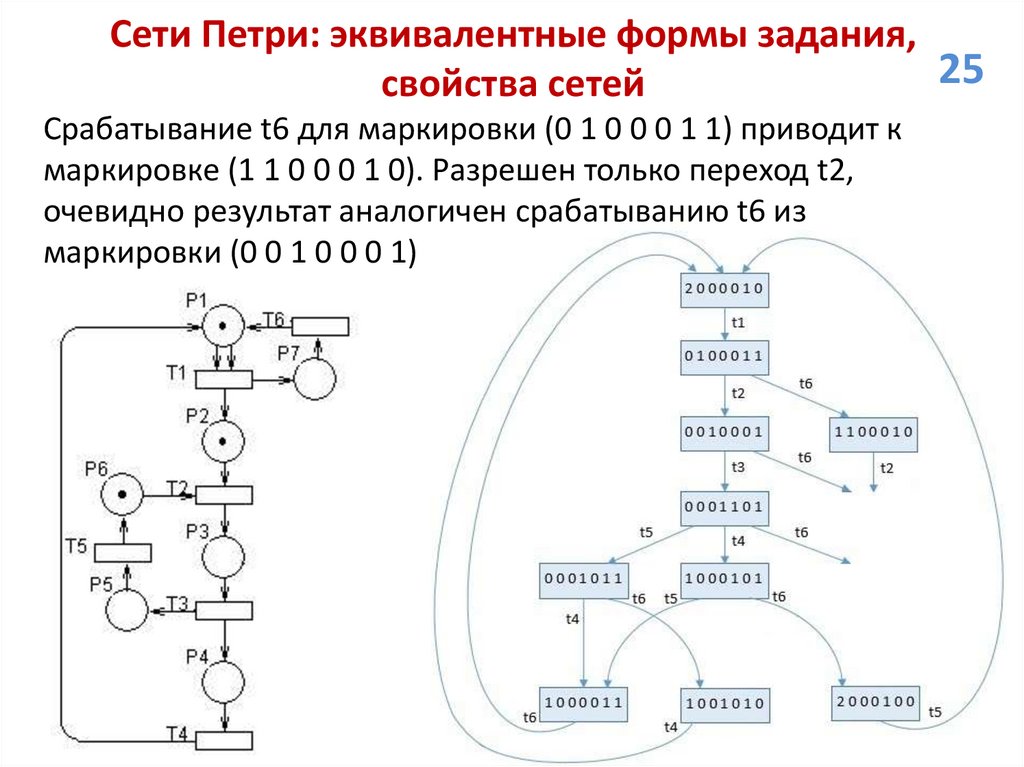
Сети Петри: эквивалентные формы задания,
25
свойства сетей
Срабатывание t6 для маркировки (0 1 0 0 0 1 1) приводит к
маркировке (1 1 0 0 0 1 0). Разрешен только переход t2,
очевидно результат аналогичен срабатыванию t6 из
маркировки (0 0 1 0 0 0 1)

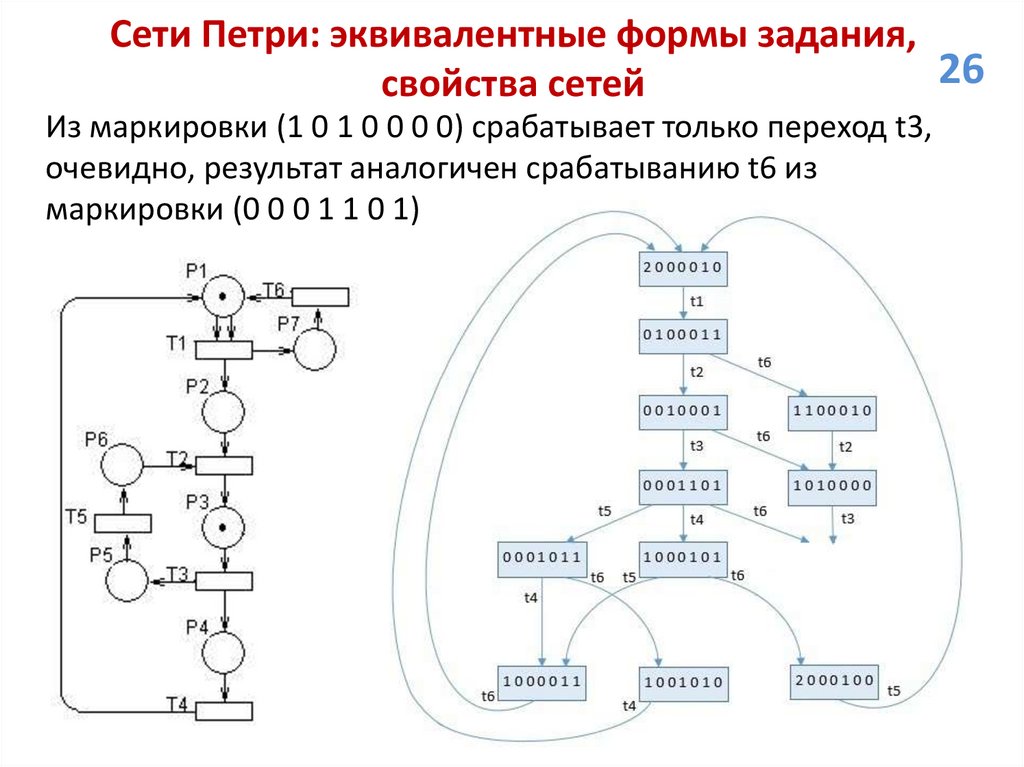
26.

Сети Петри: эквивалентные формы задания,
26
свойства сетей
Из маркировки (1 0 1 0 0 0 0) срабатывает только переход t3,
очевидно, результат аналогичен срабатыванию t6 из
маркировки (0 0 0 1 1 0 1)

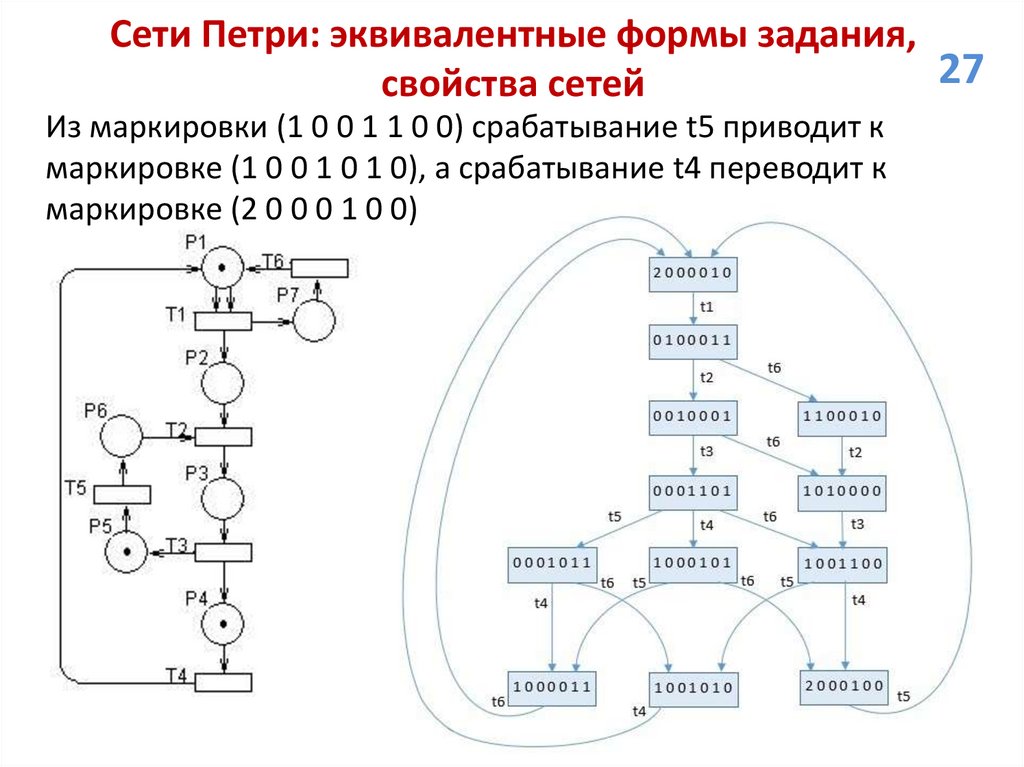
27.

Сети Петри: эквивалентные формы задания,
27
свойства сетей
Из маркировки (1 0 0 1 1 0 0) срабатывание t5 приводит к
маркировке (1 0 0 1 0 1 0), а срабатывание t4 переводит к
маркировке (2 0 0 0 1 0 0)

28.

Сети Петри: эквивалентные формы задания,
28
свойства сетей
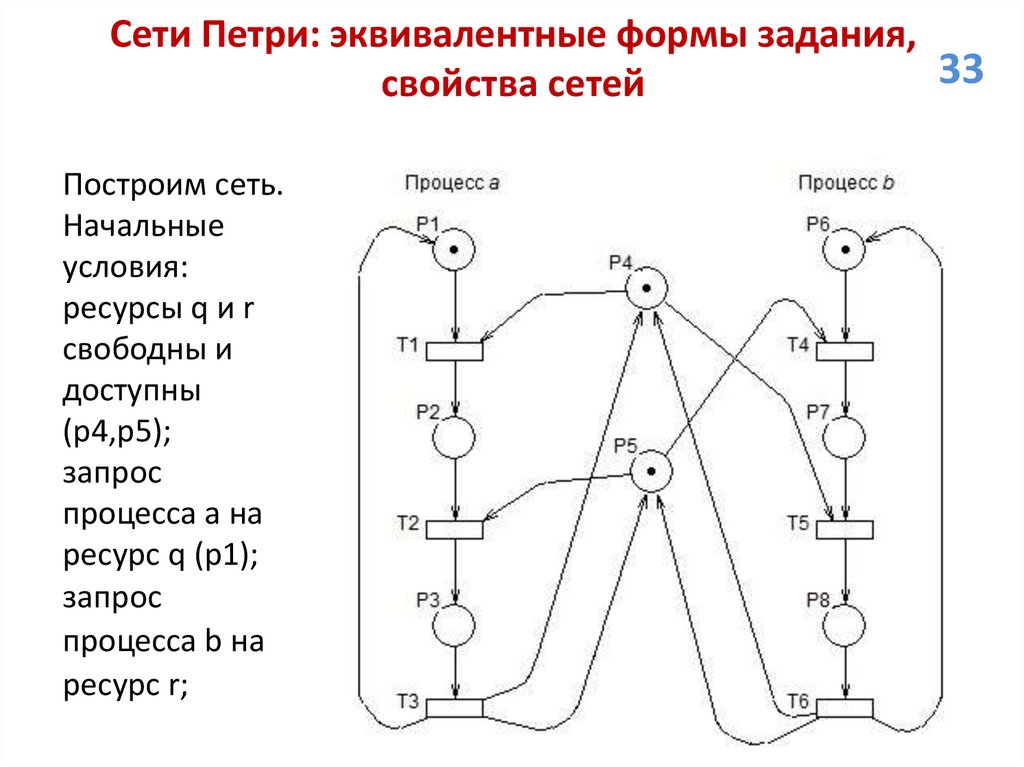
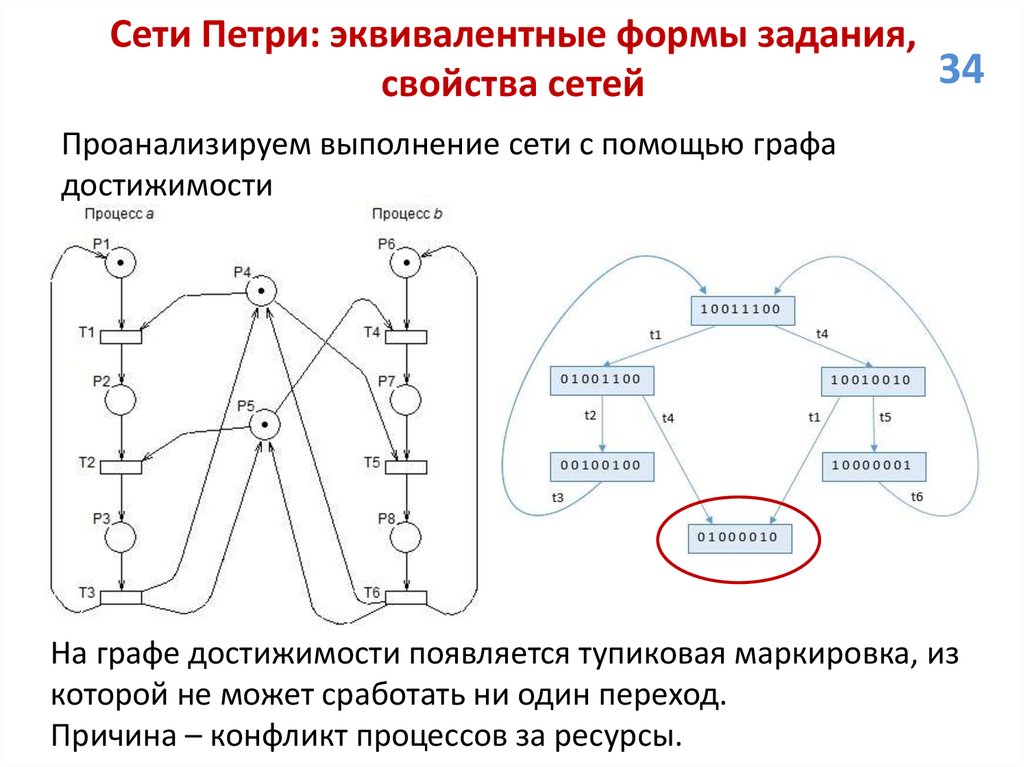
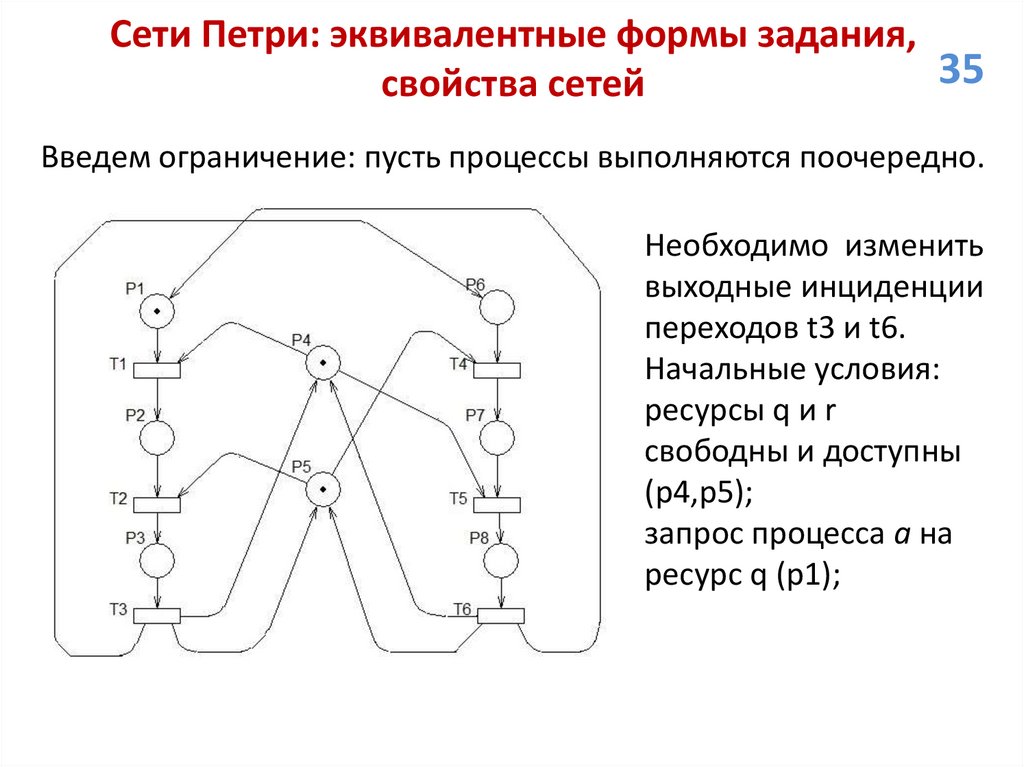
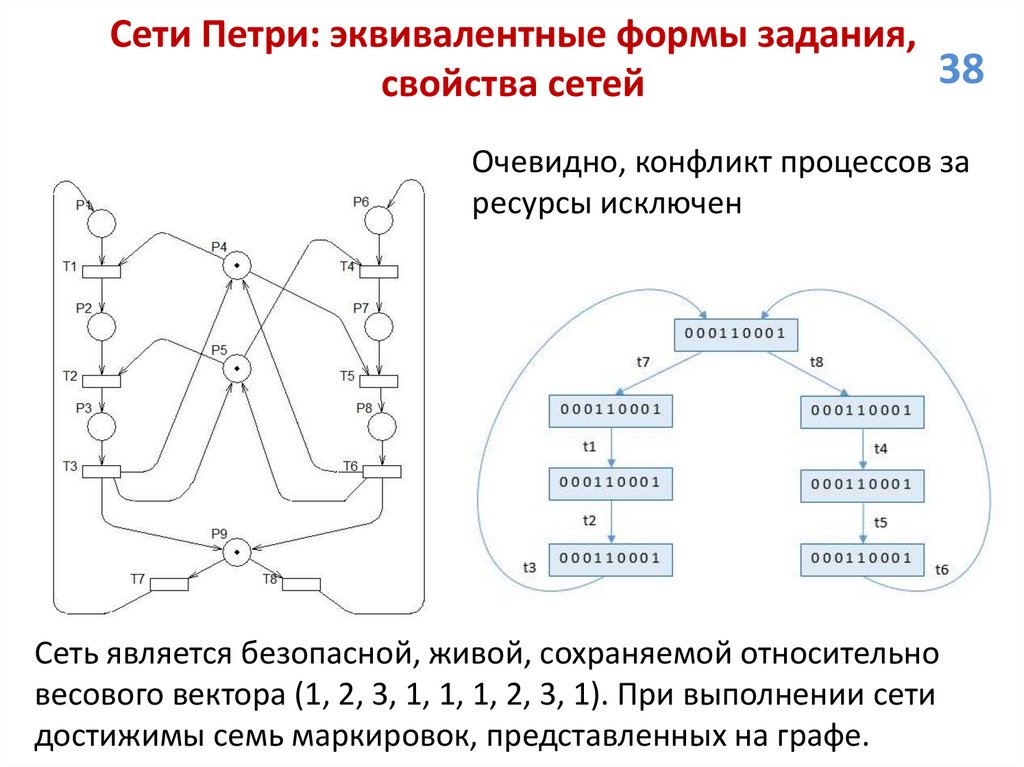
Проанализируем свойства сети.
1. Ограниченность и безопасность. Количество маркеров в
позиции p1 ограничено значением 2, остальных значением 1.
Следовательно, все позиции кроме p1 безопасны, позиция p1
является 2-ограниченной. Сеть 2-ограничена.
2. Живость. Для любой пары смежных маркировок, вторая из
который непосредственно достижима из первой, возможен
переход в первую за счет срабатывания некоторой
последовательности переходов. Сеть живая.
3. Сохраняемость. Очевидно, что для весового вектора
=(1; 1; 1; 1; 1; 1; 1) условие