Дисконтирование и наращение по учетной ставке

1.

Дисконтирование и
наращение по
учетной ставке

2. Простая учетная ставка

0
n 2
n 1
n
Pn 2
Pn 1
Sn
Pn 1 Sn dSn
Dn dSn
Dn Dn 1 ... D1 dSn
D( n ) Dn Dn 1 ... D1 ndSn
D(n ) Sn P0
P0 Sn (1 nd )
nd 1, 0 n 1
(1)

3. Пример

Вексель, погашаемый 1 января 2008 года, учтен за 10 месяцев до его
погашения на сумму 180 д.е. Какова величина годовой учетной
ставки, если ежемесячный дисконт составляет 2 д.е.?
Решение.
Дано
P0 180, D 2, n 10
Так как проценты удерживаются за каждый месяц, то за единицу
измерения времени можно принять 1 месяц.
d /12 - ежемесячная учетная ставка
D10 D9 ... D1 D 2 - дисконты за весь период
D(n) nD
P0 Sn nD Sn 200 д.е.
12 D 12 2
d
0,12
D Sn d
Sn
200
12

4. Сложная учетная ставка

0
n 2
n 1
n
Pn 2
Pn 1
Sn
Pn 1 Sn Dn , Dn d Sn
Dn 1 dPn 1 d ( Sn Dn ) dSn dDn Dn dDn Dn (1 d )
Pn 2 Sn Dn Dn 1 Pn 1 Dn 1
Dn 2 dPn 2 d ( Pn 1 Dn 1 ) dPn 1 dDn 1 Dn 1 dDn 1 Dn 1 (1 d )
или
Dn 2 Dn (1 d )2
Dn t 1 Dn t (1 d ) Dn (1 d )t 1
D1 D2 (1 d ) Dn (1 d )n 1

5. Сложная учетная ставка. Продолжение

n
D( n ) Dn Dn 1 ... D1 Dn (1 d )
t 1
n t
n 1
Dn (1 d )t
t 0
1 (1 d )n
1 (1 d )n
D(n ) Dn
dSn
Sn 1 (1 d )n
1 (1 d )
1 (1 d )
т.к.
P0 Sn D ( n ), то
P0 Sn (1 d )n
(2)

6. Пример

Государственная облигация учтена за пять лет до погашения. Какова
сумма, погашаемая по облигации, если дисконты за последний и
предпоследний годы до погашения составили соответственно 2000 и
1600 д.е.?
Решение
Используем полученные соотношения для сложных дисконтов.
Если единицей измерения времени является 1 год, то n 5 лет.
D4 1600, D5 2000
D4 D5 (1 d ) d 0,2
D5 dS5 S5 10000 д.е.

7. Дисконтирование по номинальной учетной ставке

Определение. Годовая учетная ставка g называется номинальной,
если для дисконтирования в течение 1/m части года применяется
сложная учетная ставка g/m.
g nm
P0 Sn (1 )
m
где m≥1. Если m=1, то g=d .
(3)

8. Непрерывное дисконтирование по сложной учетной ставке

Непрерывное дисконтирование - это дисконтирование
на бесконечно малых отрезках времени, т.е. при 1/m→0
(или m→∞).
g nm
P0 Sn (1 )
m
n
g m n
g m
lim (1 ) lim (1 ) ( e g ) n e g n
m
m
m
m
g
P0 Sn e n
(4)

9. Переменная учетная ставка

Рассмотрим дискретные переменные процентные ставки. Пусть n –
срок долга разбит на k участков
k
n n j
здесь k –количество периодов.
j 1
n j – продолжительность j –го промежутка, в котором
применяется учетная ставка d j ,
j 1,2,..., k
k
P0 Sn 1 n j d j
j
1
P0 Sn (1 d k )nk (1 d k 1 )nk 1 ....(1 d1 )n1

10. Наращение по учетной ставке

Если решается задача, обратная банковскому дисконтированию, то для
нахождения суммы погашаемого долга пользуются учетной ставкой.
P0
Sn
1 nd
Sn
Sn
P0
(1 d ) n
P0
g
(1 )nm
m
Если учетная ставка переменная, то получим
Sn
P0
k
1 n jd j
j 1
Sn
P0
(1 d k )nk (1 d k 1 )nk 1 ....(1 d1 )n1

11. Сравнение методов наращения

Метод наращения
Множитель наращения
По простой процентной ставке i
Формула
Sn P0 (1 in )
По сложной процентной ставке i
Sn P0 (1 i )n
(1 i ) n
По номинальной процентной
ставке j
Sn P0 (1
По постоянной силе роста δ
Sn P0e n
e n
По номинальной учетной
ставке g
P0
Sn
g
(1 )nm
m
P0
Sn
(1 d ) n
1
g
(1 )nm
m
1
P0
1 nd
1
1 nd
По сложной учетной ставке d
По простой учетной ставке d
Sn
j nm
)
m
1 in
(1
j nm
)
m
(1 d )n

12. Сравнение методов наращения.

Определение. Число, показывающее во
сколько раз наращенная сумма долга больше
первоначальной, называется множителем
наращения (или множителем накопления).
Экономический смысл множителя наращения
заключается в следующем. Если срок долга n
единиц времени, то множитель наращения
показывает накопленную к моменту n
будущую стоимость 1 д.е., вложенной в
момент t = 0 на срок n. Очевидно, что
множитель наращения больше 1.

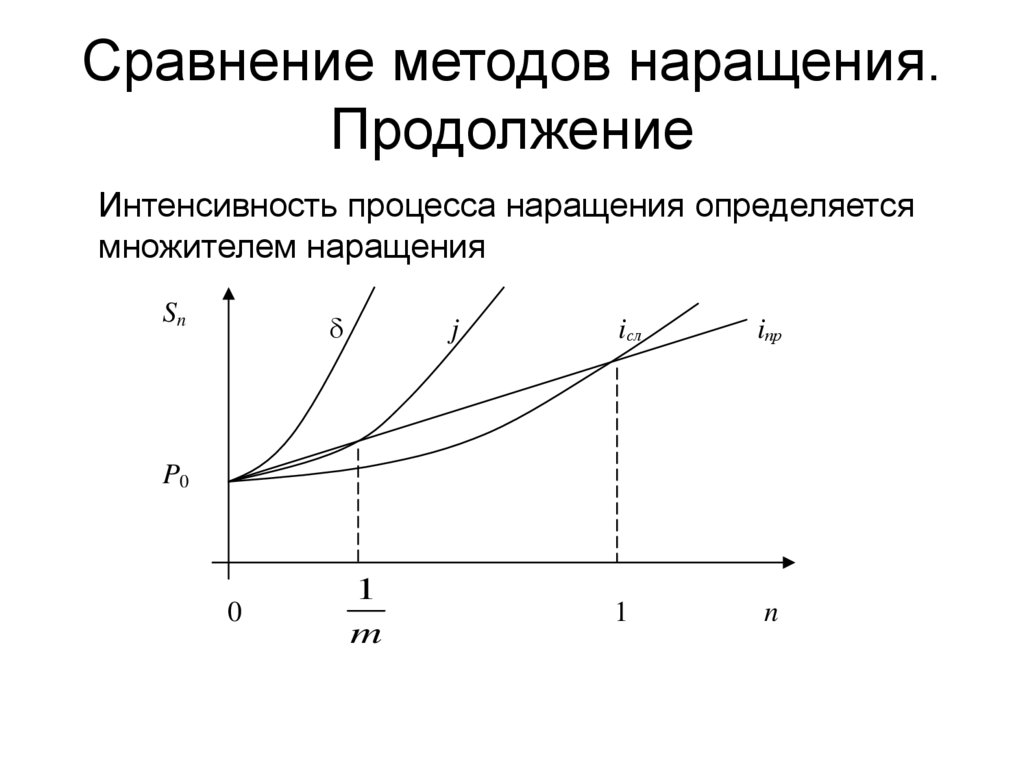
13. Сравнение методов наращения. Продолжение

Интенсивность процесса наращения определяется
множителем наращения
Sn
j
iсл
iпр
1
n
P0
0
1
m

14. Сравнение методов дисконтирования

Метод дисконтирования
Формула
По простой учетной ставке d
P0 Sn (1 nd )
1 nd
По сложной учетной ставке d
P0 Sn (1 d )n
(1 d )n
По номинальной учетной ставке
g
P0 Sn (1
По постоянной силе роста δ
P0 Sn e n
По номинальной процентной
ставке j
P0
По сложной процентной ставке i
P0
По простой процентной ставке i
P0
g nm
)
m
Sn
j
(1 )nm
m
Дисконтный множитель
(1
g nm
)
m
e n
Sn
(1 i )n
1
j
(1 )nm
m
1
(1 i ) n
Sn
1 in
1
1 in

15. Сравнение методов дисконтирования

Определение. Число, показывающее какую долю от
суммы погашаемого долга составляет его
современная величина, называется дисконтным
множителем.
Экономический смысл дисконтного множителя
заключается в следующем. Если срок долга n единиц
времени, то дисконтный множитель - это
современная стоимость 1 д.е., подлежащей выплате
через время n. Очевидно, что дисконтный множитель
меньше 1.

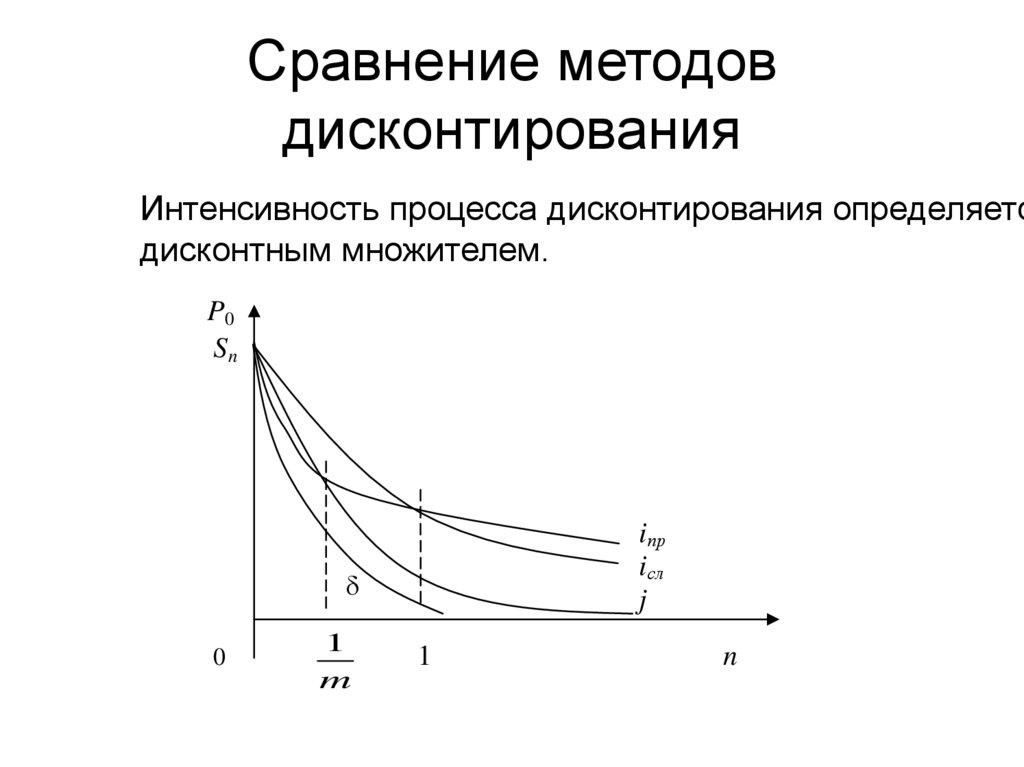
16. Сравнение методов дисконтирования

Интенсивность процесса дисконтирования определяетс
дисконтным множителем.
P0
Sn
iпр
iсл
j
0
1
m
1
n