Неявные функции

1.

Неявные функции
Пусть функция y x y x1 ,
, xm задана неявно функциональным уравнением
F x, y F x1 , , xm , y 0 .
(3.1)
Теорема о непрерывности неявной функции. Если функция F x1 ,
в некоторой окрестности точки N 0 x10 ,
, xm0 , y 0
, xm , y
m 1
1) непрерывна и F N0 0 ,
2) имеет частную производную F , непрерывную в точке N 0 и Fy N 0 0 , то
y
в некоторой окрестности точки M 0 x10 ,
ственную функцию y f x1 ,
, xm0
m
уравнение (3.1) определяет един-
, xm , причем эта функция непрерывна в рассматри-
ваемой окрестности.
1

2.

Теорема о дифференцируемости неявной функции.
Если выполнены все условия предыдущей теоремы и при этом в некоторой
окрестности точки N 0 x10 , , xm0 , y 0 m 1 существуют все частные производные
функции F x1 ,
точки M 0 x10 ,
, xm , y , непрерывные в точке N 0 , то в некоторой окрестности
, xm0
m
функция, y f x1 ,
, xm , определенная уравнением
(3.1), в точке M 0 имеет частные производные f x i , i 1, m .
Замечания:
1 . Если дополнительно потребовать непрерывность частных производных
функции F x , y в окрестности точки N 0 , то частные производные f x i , i 1, m
будут непрерывны в некоторой окрестности точки M 0 .
2 . Предыдущее замечание можно переформулировать следующим образом:
из дифференцируемости функции F x , y в окрестности точки N 0 , при выполнении условий теоремы, следует дифференцируемость функции y f x
в окрестности точки M 0 .
2

3.

Вычисление частных производных неявно заданной функции
Если выполнены все условия теоремы о дифференцируемости неявно
заданной функции, то частные производные функции y x1 ,
, xm в точке M 0
можно вычислить по формуле
Fx k
y
, k 1, m .
xk
Fy
(3.2)
При дополнительном условии непрерывности частных производных
Fy , Fx k , k 1, m
в некоторой окрестности точки N 0 формула (3.2) становится верна в
некоторой окрестности точки M 0 .
Чтобы обеспечить существование у функции y x1 ,
, xm частных
производных более высоких порядков в рассматриваемой точке, следует
потребовать,
чтобы
функция
F x1 ,
, xm , y
была
дифференцируема
соответствующее число раз в этой точке.
3

4.

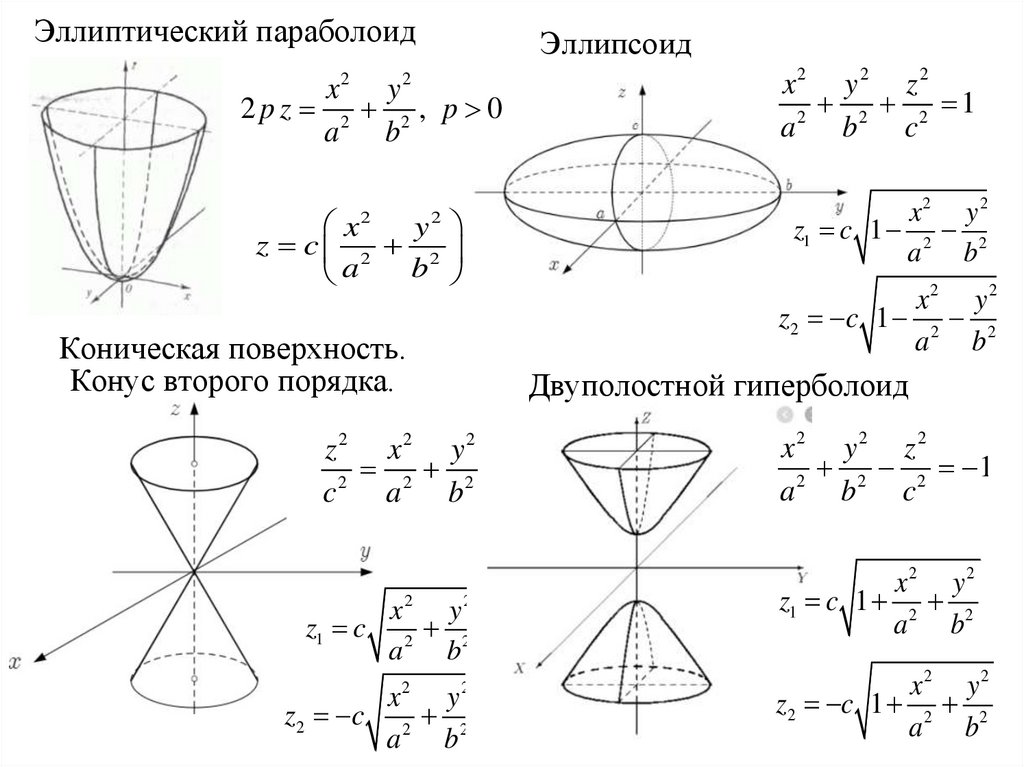
Эллиптический параболоид
Эллипсоид
x2 y 2
2pz 2 2 , p 0
a b
x2 y 2 z 2
2 2 1
2
a
b
c
x
y
z c 2 2
b
a
x2 y 2
z1 c 1 2 2
a b
2
2
Коническая поверхность.
Конус второго порядка.
Двуполостной гиперболоид
z 2 x2 y 2
2 2
2
c
a
b
x2 y 2
z1 c 2 2
a
b
2
x2 y 2
z 2 c 1 2 2
a b
2
x
y
z 2 c 2 2
a b
x2 y 2 z 2
2 2 1
2
a
b
c
x2 y 2
z1 c 1 2 2
a b
x2 y 2
z 2 c 1 2 2
a 4b

5.

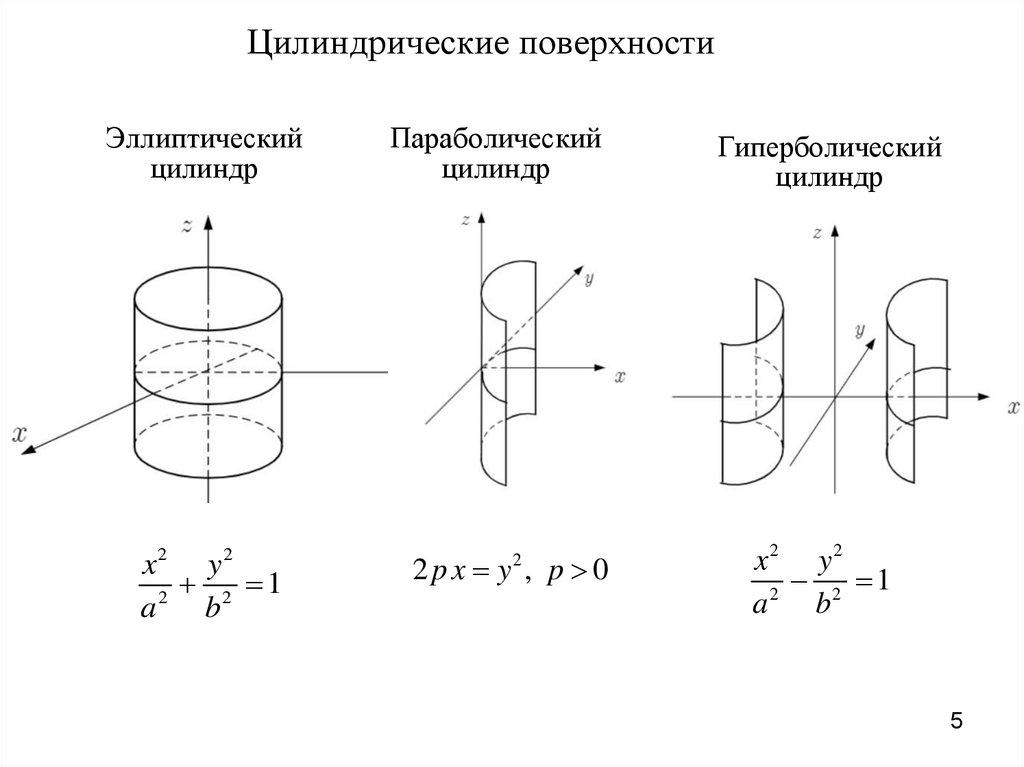
Цилиндрические поверхности
Эллиптический
цилиндр
Параболический
цилиндр
Гиперболический
цилиндр
x2 y 2
2 1
2
a
b
2p x y , p 0
x2 y 2
2 1
2
a
b
2
5

6.

x2 y 2 z 2
2 2 1
2
a
b
c
x2 y 2 z 2
F x, y , z 2 2 2 1 0
a
b
c
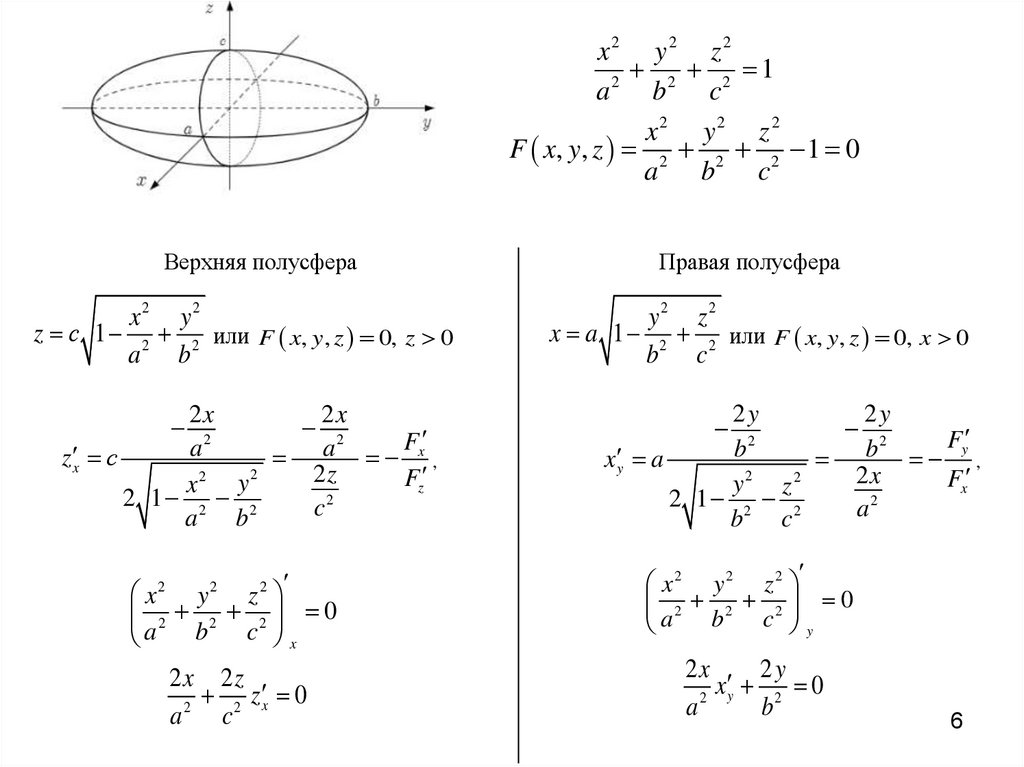
Верхняя полусфера
Правая полусфера
x2 y 2
z с 1 2 2 или F x, y, z 0, z 0
a b
y2 z2
x a 1 2 2 или F x, y, z 0, x 0
b c
2x
2x
2
F
a2
z x с
a x ,
2
2z
Fz
x2 y
2
2 1 2 2
c
a
b
2y
2y
2
2
Fy
b
b
xy a
,
2
2
2
x
Fx
y
z
2
2 1 2 2
a
b
c
x
y
z
2 2 2 0
b
c x
a
x 2 y 2 z 2
2 2 2 0
b
c y
a
2x 2z
2 z x 0
2
a c
2x
2y
x
0
2 y
2
a
b
2
2
2
6