Предел и непрерывность функции 2024

1.

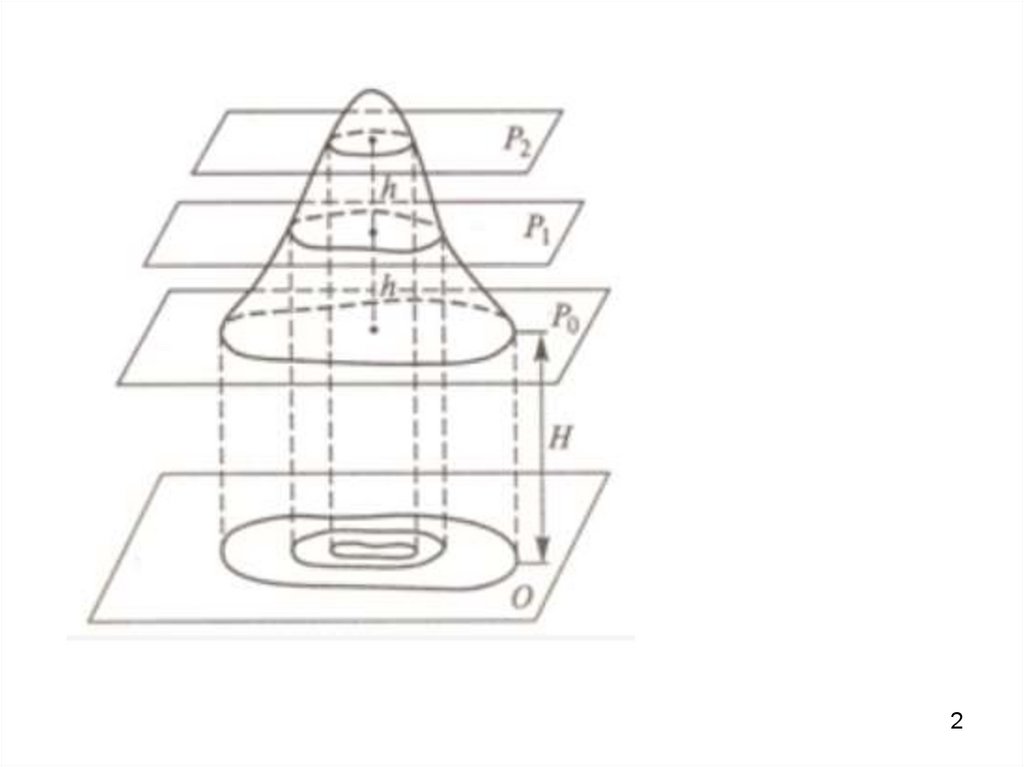
П р и м е р 1 . 1 . Найти область определения и c -уровни функций
а) u x, y ln 1 x 2 y 2 , б) w x, y, z y x .
а) Область определения функции u x, y – множество внутренних
точек единичного круга ( x 2 y 2 1 ).
Линии c -уровня: ln 1 x 2 y 2 c , т.е. x 2 y 2 1 ec :
– при c 0 – ;
– при c 0 – точка 0,0 ;
– при c 0 – окружности с центром в точке 0,0 и радиусом 1 ec .
б) Область определения функции w x, y, z – полупространство y x .
Линии c -уровня: y x c :
– при c 0 – ;
– при c 0 – плоскости y x c 2 .
1

2.

2

3.

Предел функции
lim f x b
x1 x1
x2 x20
...
xm xm0
Определение предела по Коши для функции f ( x ) , определенной
на множестве X E m
Символическая запись
x x0
lim f x lim0 f x1 , x2 ,..., xm
x x0
f x b
f x b
f x b 0
0 f x b
f x b 0
lim f x
при x x 0
f x
lim f x
f x
lim f x
f x
lim f x b
f x b
x x0
x x0
x x0
x
0 x, x 0
f x
f x
0
0
f x
x x X ,
f x b
f x b 0
f x b 0
0 b f x
0 f x b
x, O
при x
0 b f x
lim f x
f x
lim f x
f x
f x
lim f x
f x
f x
x
x
x
Определение предела по Гейне для функции f ( x ) ,
определенной на множестве X E m
Символическая запись
lim f x S ,
f x S при x x
lim f x S
f x S при x
x x0
x
f x
0
xn
lim xn x 0 и
n xn X , xn x 0 ,
lim xn и
n xn X
n
n
f xn S при n
П р и м е ч а н и е 1 . S b, b 0, b 0, , , , b . Если S b 0, b 0 , то обычно не используют запись с lim .
П р и м е ч а н и е 2 . Множество X в общем случае не совпадает с областью определения функции f ( x ) .
3
При этом говорят о пределе функции по множеству X

4.

Критерий Коши (необходимое и достаточное условие существования предельного
значения). Для того чтобы функция f x : X имела конечное предельное значение в
точке x 0 , необходимо и достаточно, чтобы она удовлетворяла в точке x 0 условию Коши:
0 A , x 0
0 0 A , A X
0
0 A , x
f A f A .
Повторные предельные значения
Пусть функция u f x, y определена в прямоугольнике
Q x, y x x0 d1 , y y0 d 2 ,
кроме, быть может, отрезков прямых x x0 , y y0 .
Пусть для любого фиксированного значения y , удовлетворяющего условию
0 y y0 d2 , существует предел функции f x, y при x x0 , т.е. определена функция:
lim f x, y y .
x x0
y фикс.
Если lim y b , то в точке x0 , y0 существует повторный предел: lim lim f x, y b .
y y0
Предел
lim
x x0
y фикс.
0 y y0 d 2
f x, y называют внутренним пределом в повторном.
Аналогично определяется повторный предел lim lim f x, y .
x x0 y y0
y y0 x x0
4

5.

Теорема 1.6. Пусть функция u f x, y определена в некоторой прямоугольной окрестности
x x0 d1 , y y0 d2 точки x0 , y0 кроме, быть может, отрезков прямых x x0 , y y0 и
lim f x, y b .
x x0
y y0
Если для любого фиксированного x , 0 x x0 d1 , существует предел x lim f x, y и
y y0
x фикс.
для любого фиксированного y , 0 y y0 d2 , существует предел y lim f x, y , то
повторные пределы lim lim f x, y и lim lim f x, y существуют и равны b .
x x0 y y0
x x0
y фикс.
y y0 x x0
0 x x0
lim f x, y b 0 0 x y
f x, y b .
x x0
0
y
y
0
y y0
lim lim f x, y lim x b 0 0 x 0 x x0 x b .
x x0 y y0
x x0
y y0 x x0
y y0
lim lim f x, y lim y b 0 0 y 0 y y0 y b .
Замечания:
1 . Из существования предела функции в точке не следует существование повторных
пределов функции в этой точке.
2 . Из существования и равенства повторных пределов функции в данной точке не следует
существование предела функции в этой точке.
3 . Если повторные пределы в точке x существуют и не равны, то предел функция в точке
x 0 не существует.
5
0

6.

x2 y
П р и м е р 1.2. Докажем по определению, что lim 2
0.
x 0 x y 2
y 0
0 x, y 0 x 2 y 2
x2 y
x2 y
2
2
0
y
x
y
.
2
2
2
2
x y
x y
П р и м е р 1.3. Вычислим предел lim 1 xy
2 / x 2 xy
x 0
y 2
1 xy
1 xy
1/ xy
.
2y
x y
.
Обозначим z xy , тогда если x 0 , y 2 , то z 0 и
2 / x 2 xy
1/ xy
lim 1 xy
x 0
y 2
lim 1 z
1/ z
z 0
e.
2y
2 / x 2 xy
e 2 .
2 , получим lim 1 xy
Учитывая, что lim
x 0
x 0 x y
y 2
y 2
6

7.

x 2y
.
x x 2 2 xy 2 y 2
y
Перейдем к полярным координатам x r cos , y r sin . Тогда
П р и м е р 1.4. Вычислим предел lim
x 2y
cos 2sin
1 f
,
2
2
2
2
x 2 xy 2 y
r cos 2cos sin 2sin r g
а условие x, y эквивалентно условию r .
Докажем ограниченность функции
f
, 0 2 .
g
f cos 2 sin 3 ,
g cos 2 2cos sin 2sin 2 cos sin sin 2 0 .
2
Так как g – непрерывна на 0, 2 , то она имеет на 0, 2 минимальное
значение, причем m min g 0 , а значит, g m 0 , поэтому
0,2
f
т.е. функция
ограничена на 0, 2 . Следовательно,
g
x 2y
lim 2
0 .
x x 2 xy 2 y 2
y
f 3
,
g m
7

8.

П р и м е р 1.5. Покажем, что lim x 2 y 2 e
x y
lim x 2 y 2 e
x y
x
y
x
y
0 , а предел
не существует.
Перейдем к полярным координатам, получим
x y e
2
x y
2
r 2e
r cos sin
.
0, , то cos sin 0 , поэтому, учитывая, что
2
показательная функция растет быстрее степенной, получаем
Если
lim x 2 y 2 e
x y
x
y
lim r 2 e
r cos sin
r
0 / 2
0.
3
Если x y
, то при x и y
4
x y e r .
2
2
x y
2
Таким образом, при разных мы получаем разные предельные
значения, а значит, предел lim x 2 y 2 e
x
y
x y
не существует.
8

9.

П р и м е р 1.6. Вычислим повторные пределы функций
ax by
x2 y 2
f x, y
, c 0, d 0 и g x, y 2
cx dy
x y2
в точке O 0,0 .
ax by
a a
lim ,
lim lim f x, y lim lim
x 0 y 0
x 0
y 0
cx dy x 0 c c
x
фикс.,
x
0
ax by
b b
lim ,
lim lim f x, y lim lim
y 0 x 0
y 0
x 0
cx dy y 0 d d
y
фикс.,
y
0
x2 y 2
lim1 1 ,
lim lim g x, y lim lim
2
2
x 0 y 0
x 0
y 0
x y x 0
x
фикс.,
x
0
x2 y 2
lim 1 1 .
lim lim g x, y lim lim
2
2
y 0 x 0
y 0
x 0
x y y 0
y фикс., y 0
9

10.

xy
имеет равные
x2 y 2
повторные пределы, но предел lim f x, y не существует.
П р и м е р 1 . 7 . В точке O 0,0 функция f x, y
x 0
y 0
xy
xy
lim lim 2
lim
lim
lim 0 0 ,
2
2
x 0 y 0 x y 2
x 0 y 0
x y x 0
x фиксир.
x 0
xy
xy
lim lim 2
lim
lim
lim 0 0 .
2
2
y 0 x 0 x y 2
y 0 x 0
x y y 0
y фиксир.
y 0
Покажем, что lim f x, y не существует.
x 0
y 0
xy
kx 2
k
y
kx
lim
Способ 1. lim 2
.
x 0 2 2 2
2
x 0 x y 2
x k x 1 k
y kx
x r cos
xy
r cos r sin
sin 2
Способ 2. 2
.
2
2
2
y
r
sin
x y
2
r cos r sin
10

11.

1
1
f x, y x y sin sin
в точке O 0,0
x
y
бесконечно малой, но повторные пределы в данной точке не существуют.
Пример
1 . 8 . Функция
является
Точка O 0,0 является предельной точкой области определения.
1
1
lim f x, y 0 , т.к. x y – БМФ, а sin sin ограниченная функция.
y 0
x
y
x 0
Рассмотрим внутренний предел
lim
x 0,
y фикс., y 0
f x, y в повторном пределе lim lim f x, y .
y 0 x 0
1 1
x sin sin 0 .
x 0,
x y
y фикс., y 0
1
2) При фиксированном y
n
n
1
1
y sin const 0 , а функция sin не имеет предела при x 0 .
x
y
1 1
1 1
Следовательно, функция f x, y x sin sin y sin sin не имеет предела
x y
x y
1
при x 0 и фиксированном y
n , а значит, не существует и повторный предел
n
lim lim f x, y .
1)
lim
y 0 x 0
11

12.

x2 y
П р и м е р . Для функции f x, y 4
предел по любой прямой,
2
x y
проходящей через точку 0,0 равен 0, но lim f не существует.
x 0
y 0
x 2 kx
kx
lim f x, y lim 4
lim 2
0.
2
y kx ,
x 0
x 0 x k 2
x kx
x 0
lim
2
y px , p 0
x 0
f x, y lim
x 0
x 2 px 2
x 4 px 2
2
p
0 .
2
1 p
12

13.

Непрерывные функции
Пусть A a1 , a2 ,..., am – предельная точка области определения X функции f x .
Приращение или полное приращение функции f x в точке A :
u f x f A f a1 x1 , a2 x2 ,..., am xm f a1 , a2 ,..., am ,
где x – любая точка из области определения функции, xi xi ai , i 1, m .
Функция u f x называется непрерывной в точке A , если выполняется одно из следующих
условий:
1) lim f x f lim x ;
x A
x A
2) 0 0 x X x, A f x f A ;
3) lim u lim f x f A lim u 0 ;
x A
x A
4) f x f A x , где lim x 0 .
x1 0
x2 0
...
xm 0
x 0
Точки разрыва функции – предельные точки области определения функции, в которых функция
не обладает свойством непрерывности.
Функция f x называется:
– непрерывной на множестве, если она непрерывна в каждой точке этого множества;
– непрерывной в точке A по кривой L , если lim f x f A ;
x A
x L
– непрерывной вдоль кривой L , если A L lim f x f A .
x A
x L
З а м е ч а н и е . Если функция f x разрывна в точке A вдоль некоторой кривой L , то точка A
является точкой разрыва этой функции. При этом может существовать кривая, вдоль которой
13
функция непрерывна.

14.

Частные приращения.
x1 u f x1 x1 , x2 ,..., xm f x1 , x2 ,..., xm ,
x2 u f x1 , x2 x2 ,..., xm f x1 , x2 ,..., xm ,
…
xm u f x1 , x2 ,..., xm xm f x1 , x2 ,..., xm .
u f x f x1 , x2 ,..., xm непрерывна в точке x по переменной xk , если
lim xk u 0 .
xk 0
З а м е ч а н и е . Непрерывность функции в точке x по отдельным переменным
x1 , x2 , …, xm представляет собой ее непрерывность на прямых, проходящих
через точку x и параллельных осям координат.
Теорема. Из непрерывности функции в точке x следует непрерывность этой
функции по каждой из переменных x1 , x2 ,..., xm .
З а м е ч а н и е : Обратное утверждение в общем случае неверно.
14

15.

Арифметические операции над непрерывными функциями.
Если функции f x и g x непрерывны в точке A , то функции
f x g x ,
f x g x ,
f x / g x
непрерывны в точке A (частное при условии g A 0 ).
Непрерывность сложной функции.
Пусть на множестве Q E k определены функции
xi i t1 , t2 ,..., tk , xi i t1 , t2 ,..., tk , i 1, m .
Тогда на Q E k определена сложная функция u f x1 , x2 ,..., xm .
Теорема о непрерывности сложной функции.
Пусть функции xi i t1 , t2 ,..., tk , i 1, m непрерывны в точке A a1 , a2 ,..., ak ,
а функция u f x1 , x2 ,..., xm непрерывна в точке
B b1 , b2 ,..., bm , bi i a1 , a2 ,..., ak , i 1, m
Тогда сложная функция u f x1 , x2 ,..., xm , xi i t1 , t2 ,..., tk , i 1, m непрерывна в
точке A .
16

16.

Теорема о сохранении знака
Если функция f x непрерывна в точке A E m и f A 0 ,
-окрестность точки A , в пределах которой f x 0 и f x f A 0 .
то
Теорема о промежуточных значениях
Пусть функция f x непрерывна во всех точках связного множества M E m .
Пусть c – любое число, заключенное между f A и f B , где A M , B M .
Тогда на любой непрерывной кривой L , соединяющей точки A и B и целиком
располагающейся в M , найдется точка Q такая, что f Q c .
Теорема Вейерштрасса об ограниченности непрерывной функции
Если функция f x непрерывна на замкнутом ограниченном множестве M ,
то она ограничена на этом множестве.
Теорема Вейерштрасса о достижении непрерывной функцией своих
точных граней. Если функция f x непрерывна на замкнутом ограниченном
множестве M , то она достигает на этом множестве своих точных верхней и
нижней граней.
17