0.97M

Категория:

Программирование

Похожие презентации:

Структуры данных

Что такое структура данных?
Структура данных — это контейнер, который хранит данные в
определенном макете. Этот «макет» позволяет структуре данных
быть эффективной в некоторых операциях и неэффективной в
других.
Структуры данных делятся на два вида:
Линейные, элементы образуют последовательность или линейный
список, обход узлов линеен. Примеры: Массивы. Связанный список,
стеки и очереди.
Нелинейные, если обход узлов нелинейный, а данные не
последовательны. Пример: граф и деревья.

3.

Основные структуры данных.
• Массивы
• Стеки
• Очереди
• Связанные списки
• Графы
• Деревья
• Префиксные деревья
• Хэш таблицы

4.

Массивы
• Массив — это самая простая и широко используемая структура
данных. Другие структуры данных, такие как стеки и очереди,
являются производными от массивов.
• Каждому элементу данных присваивается положительное
числовое значение (индекс), который соответствует позиции
элемента в массиве. Большинство языков определяют начальный
индекс массива как 0.

5.

Массивы
Бывают:
• Одномерные
• Многомерные
Основные операции
• Insert-вставляет элемент по заданному индексу
• Get-возвращает элемент по заданному индексу
• Delete-удаление элемента по заданному индексу
• Size-получить общее количество элементов в массиве

6.

Стеки
• Стек — абстрактный тип данных, представляющий
собой список элементов, организованных по
принципу LIFO (англ. last in — first out, «последним
пришёл — первым вышел»).
• Примером стека может быть куча книг,
расположенных в вертикальном порядке. Для того,
чтобы получить книгу, которая где-то посередине,
вам нужно будет удалить все книги, размещенные
на ней. Так работает метод LIFO (Last In First Out).
Функция «Отменить» в приложениях работает по
LIFO.

7.

Основные операции
• Push-вставляет элемент сверху
• Pop-возвращает верхний элемент после удаления из стека
• isEmpty-возвращает true, если стек пуст
• Top-возвращает верхний элемент без удаления из стека

8.

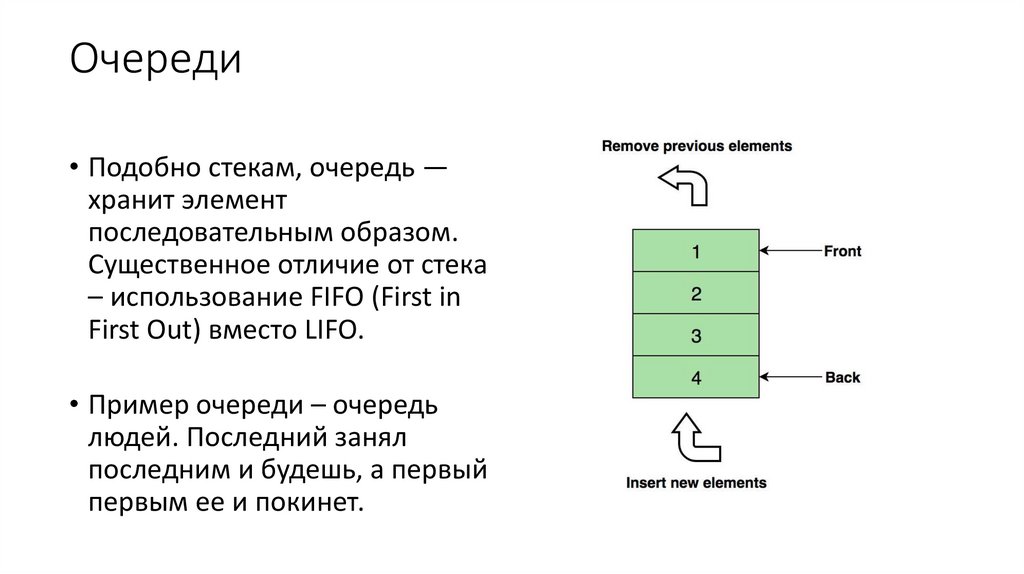
Очереди
• Подобно стекам, очередь —
хранит элемент
последовательным образом.
Существенное отличие от стека
– использование FIFO (First in
First Out) вместо LIFO.
• Пример очереди – очередь
людей. Последний занял
последним и будешь, а первый
первым ее и покинет.

9.

Основные операции
• Enqueue() — вставляет элемент в конец очереди
• Dequeue () — удаляет элемент из начала очереди
• isEmpty () — возвращает значение true, если очередь пуста
• Top () — возвращает первый элемент очереди

10.

Связанный список
• Связанный список – массив где каждый элемент является
отдельным объектом и состоит из двух элементов – данных и
ссылки на следующий узел.
• Принципиальным преимуществом перед массивом является
структурная гибкость: порядок элементов связного списка может
не совпадать с порядком расположения элементов данных в
памяти компьютера, а порядок обхода списка всегда явно
задаётся его внутренними связями.

11.

Виды связанных списков
• Однонаправленный, каждый узел хранит адрес или ссылку на следующий узел в списке
и последний узел имеет следующий адрес или ссылку как NULL.
1->2->3->4->NULL
Двунаправленный, две ссылки, связанные с каждым узлом, одним из опорных пунктов
на следующий узел и один к предыдущему узлу.
NULL<-1<->2<->3->NULL
Круговой, все узлы соединяются, образуя круг. В конце нет NULL. Циклический
связанный список может быть одно-или двукратным циклическим связанным списком.
1->2->3->1

12.

13.

Основные операции
• InsertAtEnd — Вставка заданного элемента в конец списка
• InsertAtHead — Вставка элемента в начало списка
• Delete — удаляет заданный элемент из списка
• DeleteAtHead — удаляет первый элемент списка
• Search — возвращает заданный элемент из списка
• isEmpty — возвращает True, если связанный список пуст

14.

Графы
• Граф-это набор узлов (вершин), которые соединены друг с другом
в виде сети ребрами (дугами).

15.

Графы
Виды графов
• Ориентированный, ребра являются направленными, т.е.
существует только одно доступное направление между двумя
связными вершинами.
• Неориентированные, к каждому из ребер можно осуществлять
переход в обоих направлениях.
Смешанные

16.

Графы
Встречаются в таких формах как
• Матрица смежности
• Список смежности
Общие алгоритмы обхода графа
• Поиск в ширину – обход по уровням
• Поиск в глубину – обход по вершинам

17.

Деревья
• Дерево-это иерархическая структура данных, состоящая из узлов
(вершин) и ребер (дуг). Деревья по сути связанные графы без
циклов.

18.

Типы деревьев
• N дерево
• Сбалансированное дерево
• Бинарное дерево
• Дерево Бинарного Поиска
• AVL дерево
• 2-3-4 деревья

19.

Способы обхода дерева
• В прямом порядке (сверху вниз) — префиксная форма.
• В симметричном порядке (слева направо) — инфиксная форма.
• В обратном порядке (снизу вверх) — постфиксная форма.

20.

Trie ( префиксное деревое )
• Разновидность дерева для строк,
быстрый поиск. Словари. Т9.
• Вот как такое дерево хранит слова
«top», «thus» и «their».
• Слова хранятся сверху вниз, зеленые
цветные узлы «p», «s» и «r» указывают
на конец «top», «thus « и «their»
соответственно.

21.

Хэш таблицы
• Хэширование — это процесс, используемый для уникальной
идентификации объектов и хранения каждого объекта в заранее
рассчитанном уникальном индексе (ключе).
• Объект хранится в виде пары «ключ-значение», а коллекция таких
элементов называется «словарем». Каждый объект можно найти
с помощью этого ключа.
• По сути это массив, в котором ключ представлен в виде хешфункции.

22.

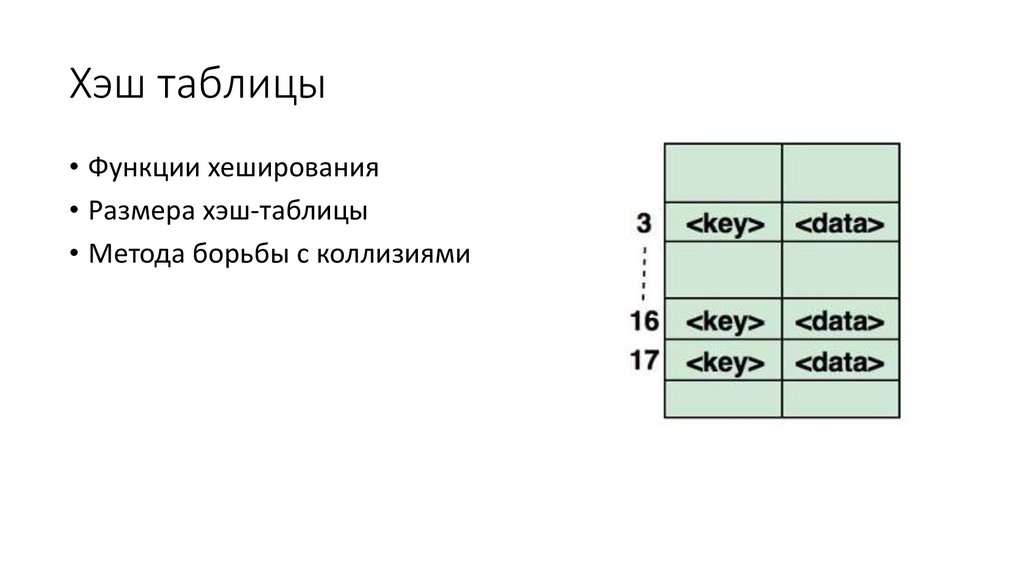
Хэш таблицы
• Функции хеширования
• Размера хэш-таблицы
• Метода борьбы с коллизиями

23.

Списки
Списком называется упорядоченное множество, состоящее из переменного
числа элементов, к которым применимы операции включения, исключения.
Список, отражающий отношения соседства между элементами, называется
линейным.
Длина списка равна числу элементов, содержащихся в списке, список нулевой
длины называется пустым списком. Списки представляют собой способ
организации структуры данных, при которой элементы некоторого типа
образуют цепочку. Для связывания элементов в списке используют систему
указателей. В минимальном случае, любой элемент линейного списка имеет
один указатель, который указывает на следующий элемент в списке или
является пустым указателем, что интерпретируется как конец списка.

24.

Однонаправленные (односвязные) списки
Однонаправленный (односвязный) список – это структура
данных, представляющая собой последовательность элементов, в
каждом из которых хранится значение и указатель на следующий
элемент списка. В последнем элементе указатель на следующий
элемент равен NULL.

25.

Описание элемента списка
Описание простейшего элемента такого списка выглядит
следующим образом:
struct имя_типа { информационное поле; адресное поле; };
где информационное поле – это поле любого, ранее объявленного
или стандартного, типа;
адресное поле – это указатель на объект того же типа, что и
определяемая структура, в него записывается адрес следующего
элемента списка.

26.

Описание элемента списка

27.

Ключ элемента
Каждый элемент списка содержит ключ, который
идентифицирует этот элемент. Ключ обычно бывает
либо целым числом, либо строкой.

28.

Основными операциями, осуществляемыми с
однонаправленными списками
создание списка;
печать (просмотр) списка;
вставка элемента в список;
удаление элемента из списка;
поиск элемента в списке
проверка пустоты списка;
удаление списка.

29.

Особое внимание следует обратить на то, что при
выполнении любых операций с линейным
однонаправленным списком необходимо обеспечивать
позиционирование какого-либо указателя на первый элемент.
В противном случае часть или весь список будет недоступен.

30.

Рассмотрим подробнее каждую из
приведенных операций
Для описания алгоритмов этих основных операций
используется следующее объявление:

31.

Создание однонаправленного списка
Для того, чтобы создать список,
нужно создать сначала первый
элемент списка, а затем при помощи
функции добавить к нему остальные
элементы. При относительно
небольших размерах списка
наиболее изящно и красиво
использование рекурсивной
функции. Добавление может
выполняться как в начало, так и в
конец списка.

32.

Печать (просмотр) однонаправленного
списка
Операция печати списка
заключается в
последовательном просмотре
всех элементов списка и
выводе их значений на экран.
Для обработки списка
организуется функция, в
которой нужно переставлять
указатель на следующий
элемент списка до тех пор, пока
указатель не станет равен NULL,
то есть будет достигнут конец
списка. Реализуем данную

33.

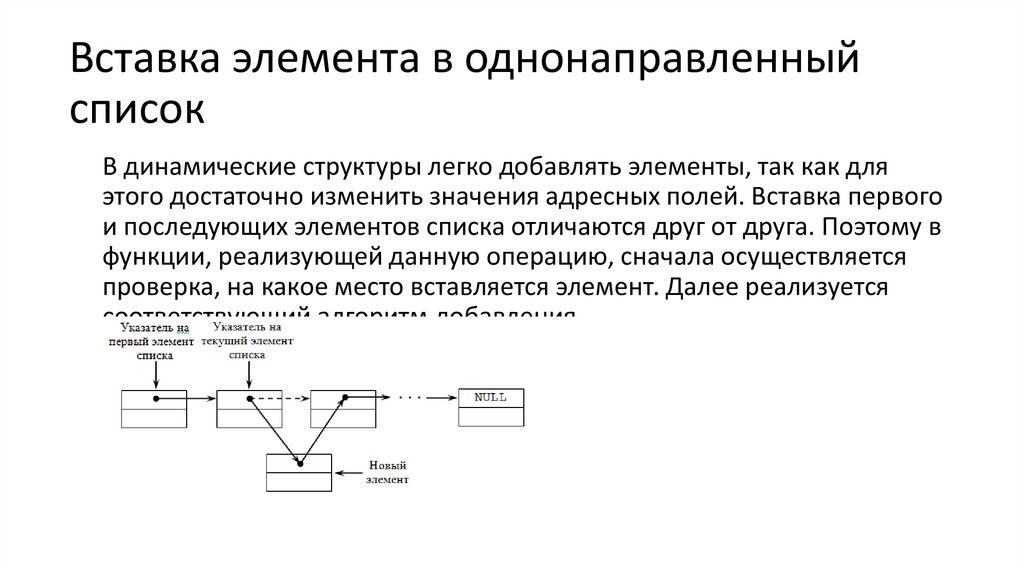
Вставка элемента в однонаправленный
список
В динамические структуры легко добавлять элементы, так как для
этого достаточно изменить значения адресных полей. Вставка первого
и последующих элементов списка отличаются друг от друга. Поэтому в
функции, реализующей данную операцию, сначала осуществляется
проверка, на какое место вставляется элемент. Далее реализуется
соответствующий алгоритм добавления

34.

35.

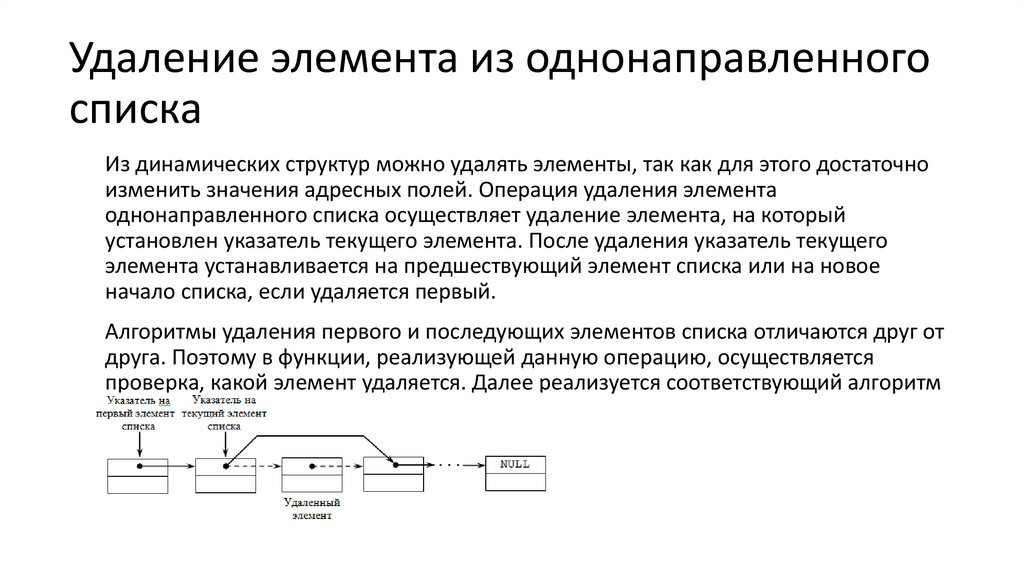
Удаление элемента из однонаправленного
списка
Из динамических структур можно удалять элементы, так как для этого достаточно
изменить значения адресных полей. Операция удаления элемента
однонаправленного списка осуществляет удаление элемента, на который
установлен указатель текущего элемента. После удаления указатель текущего
элемента устанавливается на предшествующий элемент списка или на новое
начало списка, если удаляется первый.
Алгоритмы удаления первого и последующих элементов списка отличаются друг от
друга. Поэтому в функции, реализующей данную операцию, осуществляется
проверка, какой элемент удаляется. Далее реализуется соответствующий алгоритм
удаления

36.

37.

Поиск элемента в однонаправленном
списке
Операция поиска элемента в списке заключается в
последовательном просмотре всех элементов списка до тех пор,
пока текущий элемент не будет содержать заданное значение
или пока не будет достигнут конец списка. В последнем случае
фиксируется отсутствие искомого элемента в списке (функция
принимает значение false ).

38.

Удаление однонаправленного списка
Операция удаления списка заключается в освобождении
динамической памяти. Для данной операции организуется
функция, в которой нужно переставлять указатель на следующий
элемент списка до тех пор, пока указатель не станет равен NULL,
то есть не будет достигнут конец списка. Реализуем рекурсивную
функцию.

39.

Двунаправленные (двусвязные) списки
Для ускорения многих операций целесообразно применять
переходы между элементами списка в обоих направлениях. Это
реализуется с помощью двунаправленных списков, которые
являются сложной динамической структурой.
Двунаправленный (двусвязный) список – это структура данных,
состоящая из последовательности элементов, каждый из которых
содержит информационную часть и два указателя на соседние
элементы ( рис. 29.4). При этом два соседних элемента должны
содержать взаимные ссылки друг на друга.

40.

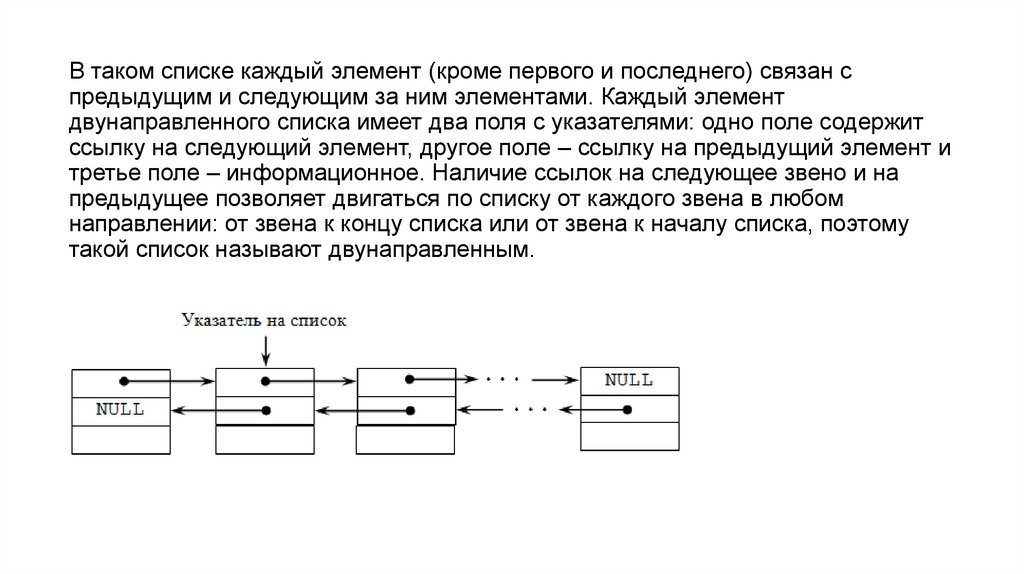
В таком списке каждый элемент (кроме первого и последнего) связан с
предыдущим и следующим за ним элементами. Каждый элемент
двунаправленного списка имеет два поля с указателями: одно поле содержит
ссылку на следующий элемент, другое поле – ссылку на предыдущий элемент и
третье поле – информационное. Наличие ссылок на следующее звено и на
предыдущее позволяет двигаться по списку от каждого звена в любом
направлении: от звена к концу списка или от звена к началу списка, поэтому
такой список называют двунаправленным.

41.

Описание простейшего элемента такого
списка
struct имя_типа {
информационное поле;
адресное поле 1;
адресное поле 2;
};
где информационное поле – это поле любого, ранее объявленного или стандартного,
типа;
адресное поле 1 – это указатель на объект того же типа, что и определяемая структура, в
него записывается адрес следующего элемента списка ;

42.

Основные операции
создание списка;
печать (просмотр) списка;
вставка элемента в список;
удаление элемента из списка;
поиск элемента в списке;
проверка пустоты списка;
удаление списка.

43.

Для описания алгоритмов этих основных операций используется
следующее объявление:

44.

Создание двунаправленного списка
Для того, чтобы создать список,
нужно создать сначала первый
элемент списка, а затем при
помощи функции добавить к нему
остальные элементы. Добавление
может выполняться как в начало,
так и в конец списка. Реализуем
рекурсивную функцию.

45.

Печать (просмотр) двунаправленного
списка
Операция печати списка
для двунаправленного
списка реализуется
абсолютно аналогично
соответствующей функции
для однонаправленного
списка. Просматривать
двунаправленный список
можно в обоих
направлениях.

46.

Вставка элемента в двунаправленный список
В динамические структуры легко добавлять элементы, так как для этого
достаточно изменить значения адресных полей. Операция вставки
реализовывается аналогично функции вставки для однонаправленного
списка, только с учетом особенностей двунаправленного списка

47.

48.

Удаление элемента из двунаправленного
списка
Из динамических структур можно удалять элементы, так как
для этого достаточно изменить значения адресных полей.
Операция удаления элемента из двунаправленного списка
осуществляется во многом аналогично удалению из
однонаправленного списка

49.

50.

Поиск элемента в двунаправленном списке
Операция поиска элемента в двунаправленном списке реализуется
абсолютно аналогично соответствующей функции для
однонаправленного списка. Поиск элемента в двунаправленном
списке можно вести:
а) просматривая элементы от начала к концу списка;
б) просматривая элементы от конца списка к началу;
в) просматривая список в обоих направлениях одновременно: от
начала к середине списка и от конца к середине (учитывая, что
элементов в списке может быть четное или нечетное количество).

51.

Поиск элемента в двунаправленном списке

52.

Проверка пустоты двунаправленного
списка

53.

Удаление двунаправленного списка

54.

Пример
N -натуральных чисел являются элементами
двунаправленного списка L, вычислить: X1*Xn+X2*Xn1+...+Xn*X1. Вывести на экран каждое произведение и
итоговую сумму.
Алгоритм:
1) Создаём структуру.
2) Формируем список целых чисел.
3) Продвигаемся по списку: от начала к концу и от конца к
началу в одном цикле, перемножаем данные,
содержащиеся в соответствующих элементах списка.
4) Суммируем полученные результаты.
5) Выводим на печать

55.

56.

Циклические (кольцевые) списки
Циклический (кольцевой) список – это структура данных,
представляющая собой последовательность элементов, последний
элемент которой содержит указатель на первый элемент списка, а
первый (в случае двунаправленного списка) – на последний.
Основная особенность такой организации состоит в том, что в этом
списке нет элементов, содержащих пустые указатели, и,
следовательно, нельзя выделить крайние элементы.
Циклические списки, так же как и линейные, бывают
однонаправленными и двунаправленными.

57.

Циклический однонаправленный список
Циклический однонаправленный список похож на линейный однонаправленный
список, но его последний элемент содержит указатель, связывающий его с первым
элементом
Для полного обхода такого списка достаточно иметь указатель на произвольный
элемент, а не на первый, как в линейном однонаправленном списке. Понятие
"первого" элемента здесь достаточно условно и не всегда требуется. Хотя иногда
бывает полезно выделить некоторый элемент как "первый" путем установки на
него специального указателя. Это требуется, например, для предотвращения
"зацикливания" при просмотре списка.

58.

Основные операции, осуществляемые с
циклическим однонаправленным списком
создание списка;
печать (просмотр) списка;
вставка элемента в список;
удаление элемента из списка;
поиск элемента в списке;
проверка пустоты списка;
удаление списка.

59.

Создание циклического однонаправленного
списка

60.

Печать циклического однонаправленного списка

61.

Вставка элемента после заданного номера
в циклический однонаправленный список

62.

Удаление элемента с заданным номером из
циклического однонаправленного списка

63.

Поиск элемента в циклическом
однонаправленном списке

64.

Проверка пустоты циклического однонаправленного списка

65.

Удаление циклического
однонаправленного списка

66.

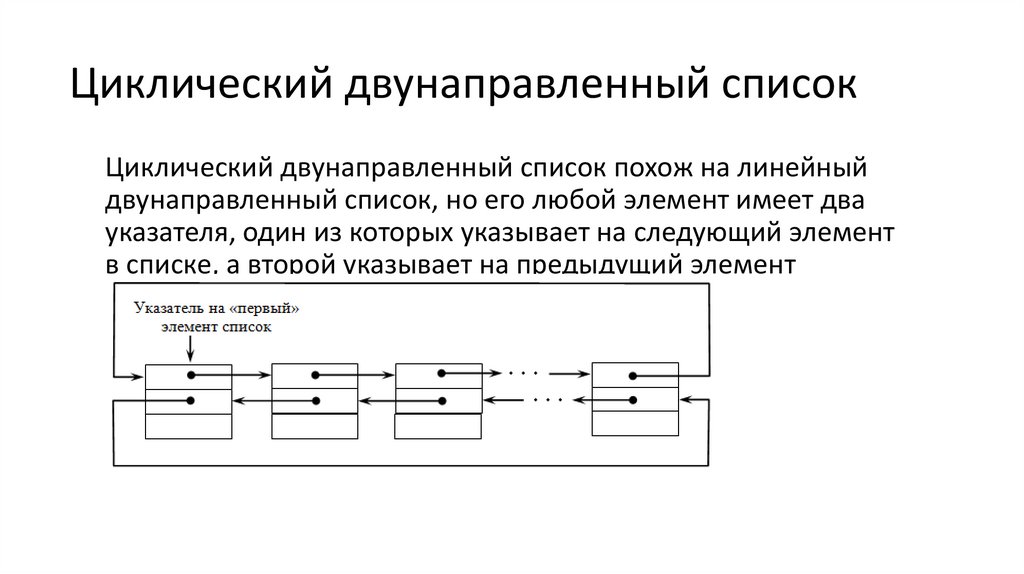
Циклический двунаправленный список
Циклический двунаправленный список похож на линейный
двунаправленный список, но его любой элемент имеет два
указателя, один из которых указывает на следующий элемент
в списке, а второй указывает на предыдущий элемент

67.

Создание циклического двунаправленного
списка

68.

Печать циклического двунаправленного
списка

69.

Вставка элемента после заданного номера в
циклический двунаправленный список

70.

Поиск элемента в циклическом
двунаправленном списке

71.

Удаление элемента с заданным номером
из циклического двунаправленного списка

72.

Проверка пустоты циклического
двунаправленного списка

73.

Удаление циклического двунаправленного
списка

74.

Деки
Дек является особым видом очереди.
Дек (англ. deque – аббревиатура от double-ended queue,
двухсторонняя очередь) – это структура данных, представляющая
собой последовательность элементов, в которой можно
добавлять и удалять в произвольном порядке элементы с двух
сторон ( рис. 32.3). Первый и последний элементы дека
соответствуют входу и выходу дека.

75.

76.

Дек и его организация
Частные случаи дека – это ограниченные деки:
дек с ограниченным входом – из конца дека можно только
извлекать элементы;
дек с ограниченным выходом – в конец дека можно только
добавлять элементы.

77.

Данная структура является наиболее универсальной из
рассмотренных выше линейных структур. Накладывая
дополнительные ограничения на операции с началом и/или
концом дека, можно осуществлять моделирование стека и
очереди.
Однако применительно к деку целесообразно говорить не о начале
и конце как в очереди, а о левом и правом конце.
Описание элементов дека аналогично описанию элементов
линейного двунаправленного списка. Поэтому объявим дек через
объявление линейного двунаправленного списка: