Структуры данных

1.

СТРУКТУРЫ ДАННЫХ
Лектор
Спиричева Наталия
Рахматулловна
Ст. преподаватель каф. ИТ
Ауд. Р-246

2.

Структуры данных
Структуры данных
Составитель курса лекций:
Спиричева Наталия Рахматулловна,
ст. преподаватель каф. Информационных технологий

3.

Структуры данных
Структуры данных
Динамические структуры данных

4.

Структуры данных
Структуры данных и алгоритмы
Основные темы лекции:
Связное представление данных в памяти
Стек
Очередь
Дек
Многосвязные списки

5.

Структуры данных
Структуры данных
Целью лекции является приобретение студентами
следующих компетенций:
знать особенности динамических структур данных
иметь представление о физической и логической структуре
уметь применять динамические структуры при
программировании

6.

Структуры данных
ДИНАМИЧЕСКИЕ СТРУКТУРЫ ДАННЫХ.
СВЯЗНЫЕ СПИСКИ
Тема 1:
Связное представление данных в памяти

7.

Структуры данных
Связное представление данных в
памяти
Динамические
структуры,
по
определению,
характеризуются отсутствием физической смежности
элементов структуры в памяти, непостоянством и
непредсказуемостью размера (числа элементов)
структуры в процессе ее обработки.

8.

Структуры данных
Связное представление данных в
памяти
Поскольку
элементы
динамической
структуры
располагаются по непредсказуемым адресам памяти,
адрес элемента такой структуры не может быть
вычислен из адреса начального или предыдущего
элемента. Для установления связи между элементами
динамической структуры используются указатели, через
которые устанавливаются явные связи между
элементами. Такое представление данных в памяти
называется связным.

9.

Структуры данных
Связное представление данных в
памяти
Элемент динамической структуры состоит из двух
полей:
информационного поля или поля данных, в котором
содержатся те данные, ради которых и создается
структура; в общем случае информационное поле
само является интегрированной структурой вектором, массивом, записью и т.п.;
поля связок, в котором содержатся один или
несколько указателей, связывающих данный элемент
с другими элементами структуры.

10.

Структуры данных
Связное представление данных в
памяти
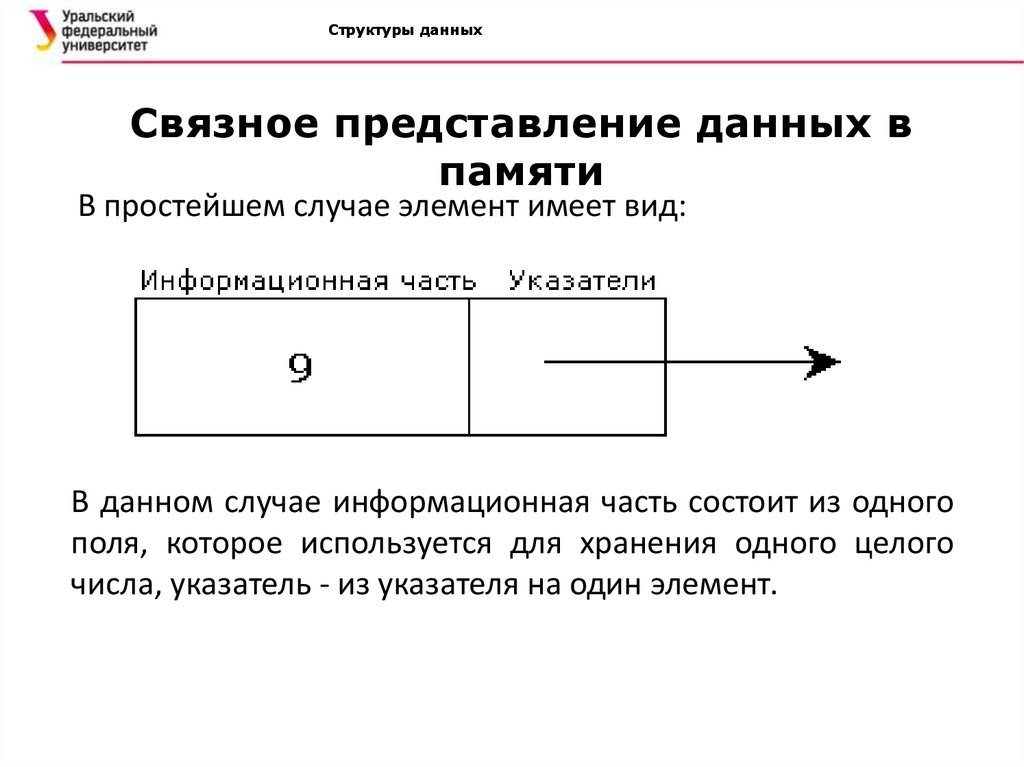
В простейшем случае элемент имеет вид:
В данном случае информационная часть состоит из одного
поля, которое используется для хранения одного целого
числа, указатель - из указателя на один элемент.

11.

Структуры данных
Связное представление данных в
памяти
Достоинства связного представления данных - в
возможности обеспечения значительной изменчивости
структур
размер структуры ограничивается только доступным
объемом машинной памяти;
при изменении логической последовательности
элементов структуры требуется не перемещение
данных в памяти, а только коррекция указателей.

12.

Структуры данных
Связное представление данных в
памяти
Вместе с тем связное представление не лишено и
недостатков, основные из которых:
работа с указателями требует, как правило, более высокой
квалификации от программиста;
на поля связок расходуется дополнительная память;
доступ к элементам связной структуры может быть менее
эффективным по времени.

13.

Структуры данных
• Списком
называется
линейно – упорядоченная
последовательность элементов данных Е.(1), Е(2), ..., Е(п),
n > О, причем каждый элемент характеризуется одним и
тем же набором попей.

14.

Структуры данных
Операции, которые имеем право
выполнять с линейными списками
1.
2.
3.
4.
5.
6.
7.
8.
9.
Получить доступ к k-му узлу списка, чтобы проанализировать и/или
изменить содержимое его полей.
Включить новый узел непосредственно перед k-м узлом.
Исключить k-й узел.
Объединить два (или более) линейных списка в один список.
Разбить линейный список на два (или более) списка.
Сделать копию линейного списка.
Определить количество узлов в списке.
Выполнить сортировку узлов списка в возрастающем порядке по
некоторым полям в узлах.
Найти в списке узел с заданным значением в некотором поле.

15.

Структуры данных
Стек – линейный список, в котором все
включения и исключения (и обычно всякий
доступ) делаются в одном конце списка.
Очередь – линейный список, в котором все
включения производятся на одном конце списка,
а все исключения (и обычно всякий доступ)
делаются на другом его конце.
Дек (очередь с двумя концами) – линейный
список, в котором все включения и исключения
(и обычно всякий доступ) делаются на обоих
концах списка.

16.

Структуры данных
ДИНАМИЧЕСКИЕ СТРУКТУРЫ ДАННЫХ.
СВЯЗНЫЕ СПИСКИ
Тема 2:
Стеки

17.

Структуры данных
Стеки
Стек - такой последовательный список с переменной длиной,
включение и исключение элементов из которого выполняются
только с одной стороны списка, называемого вершиной стека.
LIFO (Last In - First Out - "последним пришел - первым
исключился").

18.

Структуры данных
Стеки

19.

Структуры данных
Стеки
Основные операции над стеком:
включение нового элемента
исключение элемента из стека
Вспомогательные операции:
определение текущего числа элементов в стеке;
очистка стека;
неразрушающее чтение элемента из вершины стека, которое
может быть реализовано как комбинация основных операций:
x:=pop(stack);
push(stack,x).

20.

Структуры данных
Стеки
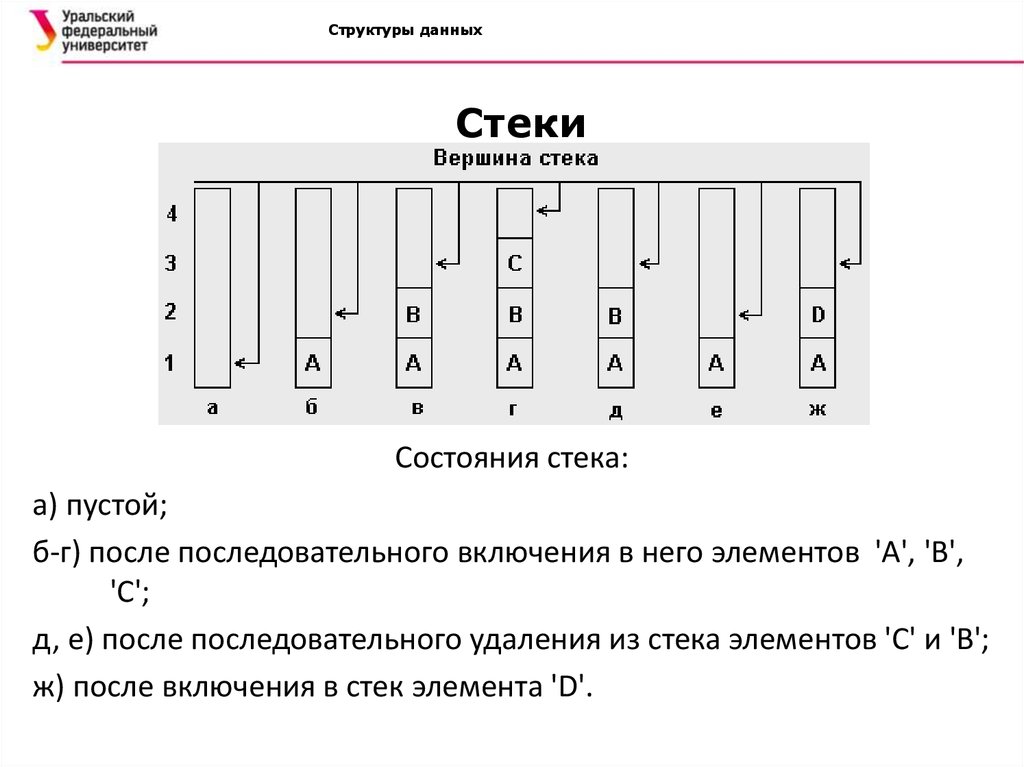
Состояния стека:
а) пустой;
б-г) после последовательного включения в него элементов 'A', 'B',
'C';
д, е) после последовательного удаления из стека элементов 'C' и 'B';
ж) после включения в стек элемента 'D'.

21.

Структуры данных
Машинное представление стека и реализация операций
При представлении стека в статической памяти для него
выделяется память, как для вектора. В дескрипторе этого
вектора кроме обычных для вектора параметров должен
находиться также указатель стека - адрес вершины стека.
Указатель стека может указывать либо на первый свободный
элемент стека, либо на последний записанный в стек элемент.
При занесении элемента в стек элемент записывается на
место, определяемое указателем стека, затем указатель
модифицируется таким образом, чтобы он указывал на
следующий свободный. Модификация указателя состоит в
прибавлении к нему или в вычитании из него единицы.

22.

Структуры данных
Стеки
Операция
исключения
элемента
состоит
в
модификации указателя стека и выборке значения, на
которое указывает указатель стека. После выборки слот,
в котором размещался выбранный элемент, считается
свободным.

23.

Структуры данных
Стеки
Операция очистки стека сводится к записи в
указатель стека начального значения - адреса начала
выделенной области памяти.

24.

Структуры данных
Стеки
Определение размера стека сводится к вычислению
разности указателей: указателя стека и адреса начала
области.

25.

Структуры данных
Стеки
Стеки в вычислительных системах
Стек является чрезвычайно удобной структурой данных
для многих задач вычислительной техники. Наиболее
типичной из таких задач является обеспечение вложенных
вызовов функций.

26.

Структуры данных
Стеки
В 1920 г. польский математик Ян Лукашевич предложил
способ записи арифметических формул, не использующий
скобок. В привычной нам записи знак операции
записывается между аргументами, например, сумма чисел 2
и 3 записывается как 2 + 3. Ян Лукашевич предложил две
другие формы записи: префиксная форма, в которой знак
операции записывается перед аргументами, и постфиксная
форма, в которой знак операции записывается после
аргументов. В префиксной форме сумма чисел 2 и 3
записывается как + 2 3, в постфиксной — как 2 3 +. В честь
Яна Лукашевича эти формы записи называют прямой и
обратной польской записью.

27.

Структуры данных
Стеки
В польской записи скобки не нужны. Например, выражение
(2+3)*(15-7)
записывается в прямой польской записи как
* + 2 3 - 15 7,
в обратной польской записи — как
2 3 + 15 7 - *.
Если прямая польская запись не получила большого
распространения, то обратная оказалась чрезвычайно
полезной. Неформально преимущество обратной записи
перед прямой польской записью или обычной записью
можно объяснить тем, что гораздо удобнее выполнять
некоторое действие, когда объекты, над которыми оно
должно быть совершено, уже даны.

28.

Структуры данных
Стеки
Обратная польская запись формулы позволяет вычислять
выражение
любой
сложности,
используя
стек
как
запоминающее устройство для хранения промежуточных
результатов. Такой стековый калькулятор был впервые выпущен
фирмой Hewlett Packard. Обычные модели калькуляторов не
позволяют вычислять сложные формулы без использования
бумаги и ручки для записи промежуточных результатов. В
некоторых моделях есть скобки с одним или двумя уровнями
вложенности, но более сложные выражения вычислять
невозможно. Также в обычных калькуляторах трудно понять, как
результат и аргументы перемещаются в процессе ввода и
вычисления между регистрами калькулятора. Калькулятор
обычно имеет регистры X, Y и регистр памяти, промежуточные
результаты каким-то образом перемещаются по регистрам,
каким именно — запомнить невозможно.

29.

Структуры данных
Стеки
Для вычисления выражения надо сначала преобразовать его
в обратную польскую запись (при некотором навыке это легко
сделать в уме). В приведенном выше примере выражение
(2+3)*(15-7) преобразуется к
2 3 + 15 7 - *
Затем
обратная
польская
запись
просматривается
последовательно слева направо. Если мы видим число, то
просто вводим его в калькулятор, т.е. добавляем его в стек.
Если мы видим знак операции, то нажимаем соответствующую
клавишу калькулятора, выполняя таким образом операцию с
числами на вершине стека.

30.

Структуры данных
ДИНАМИЧЕСКИЕ СТРУКТУРЫ ДАННЫХ.
СВЯЗНЫЕ СПИСКИ
Тема 3:
Очереди FIFO

31.

Структуры данных
Очереди FIFO
Логическая структура очереди
Очередью FIFO (First In - First Out - "первым пришел первым
исключается")
называется
такой
последовательный список переменной длины, в котором
включение элементов выполняется только с одной
стороны списка (эту сторону часто называют концом или
хвостом очереди), а исключение - с другой стороны
(называемой началом или головой очереди).
Очереди в магазинах являются типичным бытовым
примером очереди FIFO.

32.

Структуры данных
Очереди FIFO
Из
динамических
элементов
формируется
цепочка.
Динамический элемент хранит адрес следующего динамического
элемента.
Очередь работает по тому же принципу, что и очередь в
магазине: "первым пришел, первым ушел". Элементы добавляются
в конец очереди, а берутся из начала. Для работы необходимо знать
начало и конец очереди.
Указатель у последнего элемента в очереди хранит нулевое
значение

33.

Структуры данных
Очереди FIFO
Основные операции над очередью - те же, что и над стеком:
включение
исключение
определение размера
очистка,
неразрушающее чтение.

34.

Структуры данных
Очереди FIFO
Машинное представление очереди FIFO и реализация
операций
При представлении очереди вектором в статической
памяти в дополнение к обычным для дескриптора вектора
параметрам в нем должны находиться два указателя: на
начало очереди (на первый элемент в очереди) и на ее конец
(первый свободный элемент в очереди).
При включении элемента в очередь элемент записывается
по адресу, определяемому указателем на конец, после чего
этот указатель увеличивается на единицу.
При исключении элемента из очереди выбирается
элемент, адресуемый указателем на начало, после чего этот
указатель уменьшается на единицу.

35.

Структуры данных
Очереди FIFO
Возможны, конечно, и другие варианты организации
очередей: например, всякий раз, когда указатель конца
достигнет верхней границы памяти, сдвигать все непустые
элементы очереди к началу области памяти, но как этот, так и
другие варианты, требуют перемещения в памяти элементов
очереди и менее эффективны, чем кольцевая очередь.

36.

Структуры данных
Очереди FIFO
Очереди с приоритетами
В реальных задачах иногда возникает необходимость в
формировании очередей, отличных от FIFO или LIFO. Порядок
выборки элементов из таких очередей определяется
приоритетами элементов. Приоритет в общем случае может
быть представлен числовым значением, которое вычисляется
либо на основании значений каких-либо полей элемента,
либо на основании внешних факторов. Так, и FIFO, и LIFOочереди могут трактоваться как приоритетные очереди, в
которых приоритет элемента зависит от времени его
включения в очередь. При выборке элемента всякий раз
выбирается элемент с наибольшим приоритетом.

37.

Структуры данных
Очереди FIFO
Очереди с приоритетами могут быть реализованы на
линейных списковых структурах - в смежном или связном
представлении. Возможны очереди с приоритетным
включением - в которых последовательность элементов
очереди все время поддерживается упорядоченной, т.е.
каждый новый элемент включается на то место в
последовательности, которое определяется его приоритетом, а
при исключении всегда выбирается элемент из начала.
Возможны и очереди с приоритетным исключением - новый
элемент включается всегда в конец очереди, а при исключении
в очереди ищется (этот поиск может быть только линейным)
элемент с максимальным приоритетом и после выборки
удаляется из последовательности. И в том, и в другом варианте
требуется поиск, а если очередь размещается в статической
памяти - еще и перемещение элементов.

38.

Структуры данных
Очереди FIFO
Очереди в вычислительных системах
Идеальным
примером
кольцевой
очереди
в
вычислительной системы является буфер клавиатуры в Базовой
системе ввода-вывода ПЭВМ IBM PC. Буфер клавиатуры
занимает последовательность байтов памяти по адресам от
40:1E до 40:2D включительно. По адресам 40:1A и 40:1C
располагаются указатели на начало и конец очереди
соответственно. При нажатии на любую клавишу генерируется
прерывание 9. Обработчик этого прерывания читает код
нажатой клавиши и помещает его в буфер клавиатуры - в конец
очереди. Коды нажатых клавиш могут накапливаться в буфере
клавиатуры, прежде чем они будут прочитаны программой.
Программа при вводе данных с клавиатуры обращается к
прерыванию 16H. Обработчик этого прерывания выбирает код
клавиши из буфера - из начала очереди - и передает в
программу.

39.

Структуры данных
Очереди FIFO
Очередь является одним из ключевых понятий в
многозадачных операционных системах (Windows NT, Unix, OS/2, ЕС
и др.). Ресурсы вычислительной системы (процессор, оперативная
память, внешние устройства и т.п.) используются всеми задачами,
которые одновременно выполняются в среде такой операционной
системы. Поскольку многие виды ресурсов реально не допускают
одновременного их использования разными задачами, такие
ресурсы предоставляются задачам поочередно. Таким образом,
задачи, претендующие на использование того или иного ресурса,
выстраиваются в очередь к этому ресурсу. Эти очереди обычно
приоритетные, однако, довольно часто применяются и FIFOочереди, так как это единственная логическая организация
очереди, которая гарантированно не допускает постоянного
вытеснения задачи более приоритетными. LIFO-очереди обычно
используются операционными системами для учета свободных
ресурсов.

40.

Структуры данных
Очереди FIFO
Также в современных операционных системах одним
из средств взаимодействия между параллельно
выполняемыми задачами являются очереди сообщений,
называемые также почтовыми ящиками. Каждая задача
имеет свою очередь - почтовый ящик, и все сообщения,
отправляемые ей от других задач, попадают в эту очередь.
Задача-владелец очереди выбирает из нее сообщения,
причем может управлять порядком выборки - FIFO, LIFO
или по приоритету.

41.

Структуры данных
Очереди FIFO
Логическая структура очереди
FIFO (First In - First Out - "первым пришел - первым
исключается")
последовательный список переменной длины, в котором
включение элементов выполняется только с одной
стороны списка,а исключение - с другой стороны.
Основные операции над очередью:
включение
исключение
определение размера
очистка
неразрушающее чтение

42.

Структуры данных
Очереди FIFO
Очереди с приоритетами
Порядок выборки элементов из очередей определяется
приоритетами элементов. Приоритет в общем случае может
быть
представлен
числовым
значением,
которое
вычисляется либо на основании значений каких-либо полей
элемента, либо на основании внешних факторов.
FIFO, и LIFO-очереди могут трактоваться как
приоритетные очереди, в которых приоритет элемента
зависит от времени его включения в очередь. При выборке
элемента всякий раз выбирается элемент с наибольшим
приоритетом.

43.

Структуры данных
ДИНАМИЧЕСКИЕ СТРУКТУРЫ ДАННЫХ.
СВЯЗНЫЕ СПИСКИ
Тема 4:
Деки

44.

Структуры данных
Деки
Логическая структура дека
Дек особый вид очереди в виде последовательного
списка, в котором как включение, так и исключение
элементов может осуществляться с любого из двух
концов списка.
Над деком определены следующие операции:
включение элемента справа;
включение элемента слева;
исключение элемента справа;
исключение элемента слева;
определение размера;
очистка.

45.

Структуры данных
Деки
Состояния дека в процессе изменения

46.

Структуры данных
ДИНАМИЧЕСКИЕ СТРУКТУРЫ ДАННЫХ.
СВЯЗНЫЕ СПИСКИ
Тема 5:
Связные линейные списки

47.

Структуры данных
Связные линейные списки
Машинное представление связных линейных списков
Поле INF - информационное поле, данные, NEXT - указатель
на следующий элемент списка.
Каждый список должен иметь особый элемент,
называемый указателем начала списка или головой списка,
который обычно по формату отличен от остальных элементов. В
поле указателя последнего элемента списка находится
специальный признак NULL, свидетельствующий о конце списка

48.

Структуры данных
Связные линейные списки
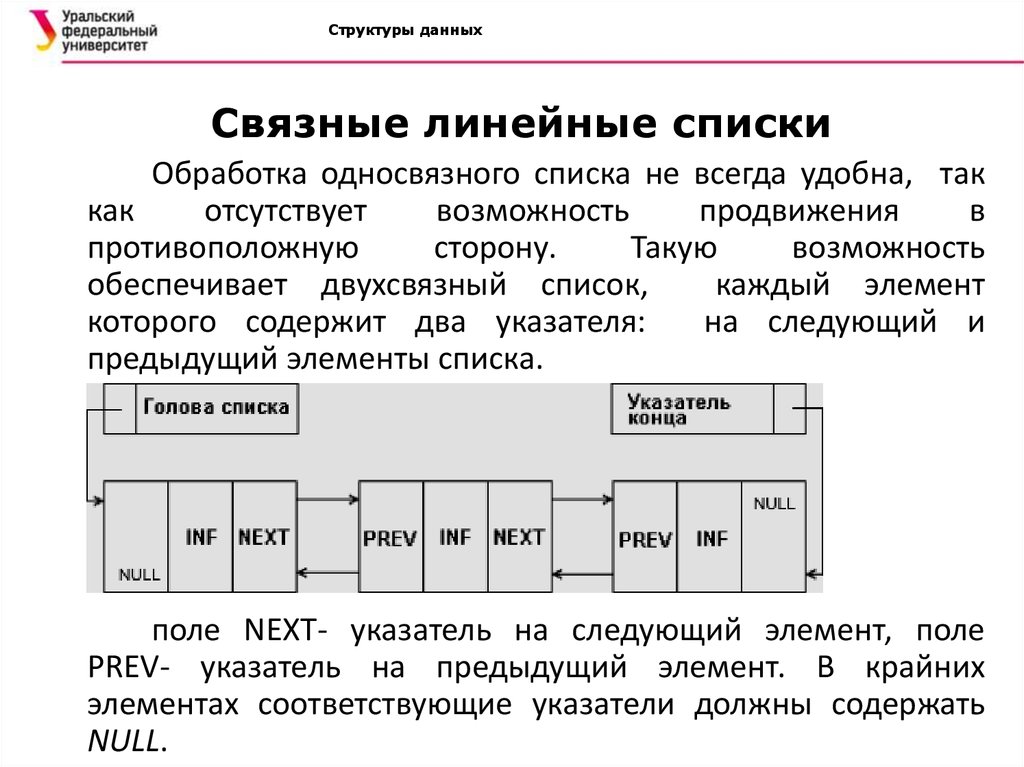
Обработка односвязного списка не всегда удобна, так
как
отсутствует
возможность
продвижения
в
противоположную
сторону.
Такую
возможность
обеспечивает двухсвязный список,
каждый элемент
которого содержит два указателя:
на следующий и
предыдущий элементы списка.
поле NEXT- указатель на следующий элемент, поле
PREV- указатель на предыдущий элемент. В крайних
элементах соответствующие указатели должны содержать
NULL.

49.

Структуры данных
Связные линейные списки
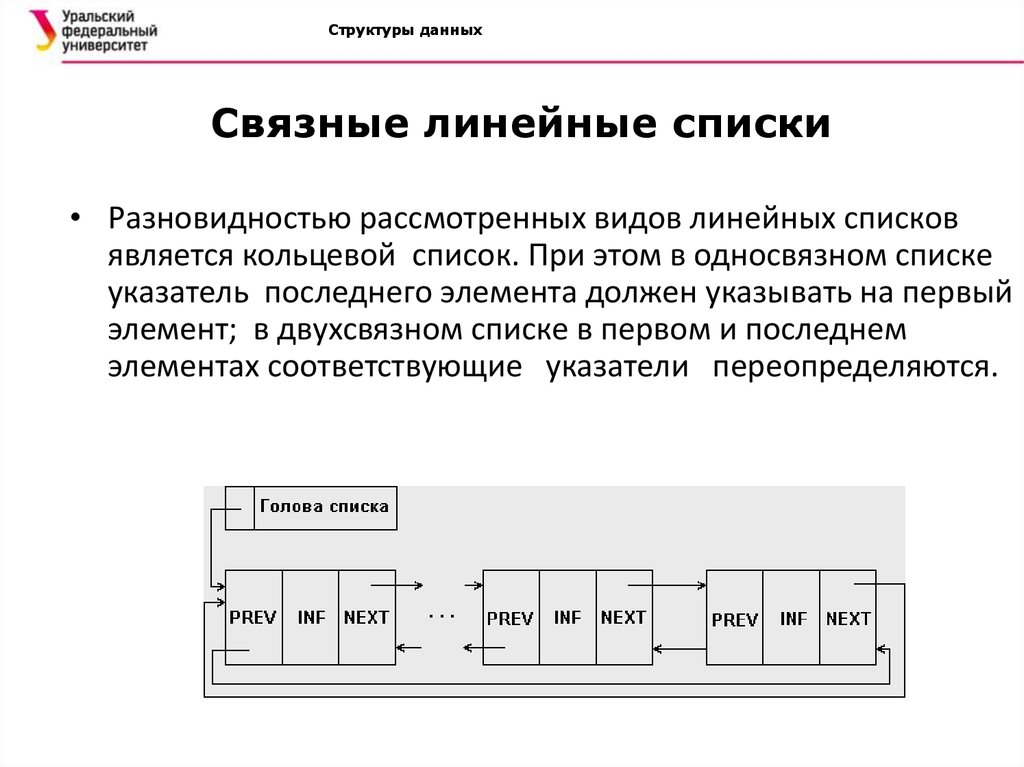
• Разновидностью рассмотренных видов линейных списков
является кольцевой список. При этом в односвязном списке
указатель последнего элемента должен указывать на первый
элемент; в двухсвязном списке в первом и последнем
элементах соответствующие указатели переопределяются.

50.

Структуры данных
Связные линейные списки
Реализация операций над связными линейными списками
Перебор
элементов
списка.
Осуществляется
последовательный доступ к элементам списка - ко всем до
конца списка или до нахождения искомого элемента.
void LookSll( link head )
{ link curr = head;
while( curr )
{
curr = curr->next;
}
}

51.

Структуры данных
Связные линейные списки
В двухсвязном списке возможен перебор как в
прямом направлении, так и в обратном. В последнем
случае параметром процедуры должен быть tail указатель на конец списка, и переход к следующему
элементу должен осуществляться по указателю назад:
curr = curr->prev;

52.

Структуры данных
Связные линейные списки
В кольцевом списке окончание перебора должно
происходить не по признаку последнего элемента - такой
признак отсутствует, а по достижению элемента, с
которого начался перебор.

53.

Структуры данных
Связные линейные списки
Вставка элемента в список.
void InsertSll( link& prev, data inf )
{ if( prev )
{
link curr = new SllNode;
curr->inf = inf;
curr->next = prev->next;
prev->next = curr;
}
}
Вставка элемента в середину 1-связного списка

54.

Структуры данных
Связные линейные списки
Вставка элемента в середину 2-связного списка

55.

Структуры данных
Связные линейные списки
Вставка элемента в начало 1-связного списка

56.

Структуры данных
Связные линейные списки
Удаление элемента из списка
void DeleteSll( link& head, link del )
{
if( head == NULL ) return;
if( del == head )
{
head = del->next;
}
else
{
link prev = head;
Удаление элемента из односвязного
списка
while( prev->next && prev->next !=
del ) prev = prev->next;
if( prev->next == del )
{prev->next = del->next;
}
}
if( del ) delete del;
}

57.

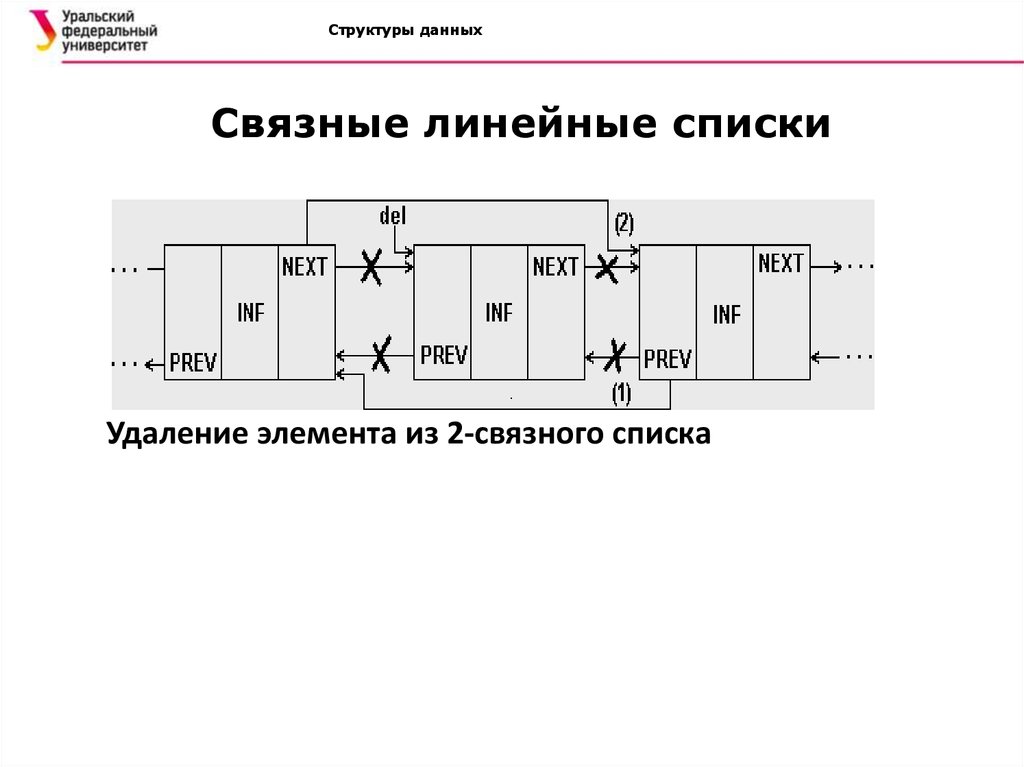
Структуры данных
Связные линейные списки
Удаление элемента из 2-связного списка

58.

Структуры данных
Связные линейные списки
Перестановка элементов списка
void ExchangeSll( link& prev )
{ if( prev && prev->next && prev->next->next )
{
link p1 = prev->next;
link p2 = p1->next;
p1->next = p2->next;
P2->next = p1;
prev->next = p2;
}
}

59.

Структуры данных
Связные линейные списки
Перестановка соседних элементов 2-связного списка

60.

Структуры данных
Связные линейные списки
Копирование части списка
При копировании старый список сохраняется в памяти
и создается новый список. В информационных полях
элементов нового списка содержатся те же данные, что и в
элементах старого списка, но поля связок в новом списке
совершенно другие, поскольку элементы нового списка
расположены по другим адресам в памяти.

61.

Структуры данных
Связные линейные списки
Алгоритм копирования
части списка:
link CopyList( link head, int num )
{ if( head == NULL ) return NULL;
link first = NULL, last = NULL;
while( head && num>0 )
{
link curr = new SllNode;
curr->next = NULL;
curr->inf = head->inf;
if( first == NULL )
{
first = curr;
last = first;
else
{
last->next = curr;
last = curr;
head = head->next;
num--;
last->next = NULL;
return first;}
}
}
}

62.

Структуры данных
Связные линейные списки
Слияние двух списков
Операция слияния заключается в формировании из двух списков
одного - она аналогична операции сцепления строк. В случае
односвязного списка: последний элемент первого списка содержит
пустой указатель на следующий элемент, этот указатель служит
признаком конца списка. Вместо этого пустого указателя в последний
элемент первого списка заносится указатель на начало второго списка.
Таким образом, второй список становится продолжением первого.
void Unit( link& Head1, link Head2 )
{
if( Head2 )
{
if(Head1 == NULL ) Head1 = Head2;
else
{
link curr = Head1;
while( curr->next ) curr = curr->next;
curr->next = Head2; }
Head2 = NULL; }
}

63.

Структуры данных
ДИНАМИЧЕСКИЕ СТРУКТУРЫ ДАННЫХ.
СВЯЗНЫЕ СПИСКИ
Тема 6:
Мультисписки

64.

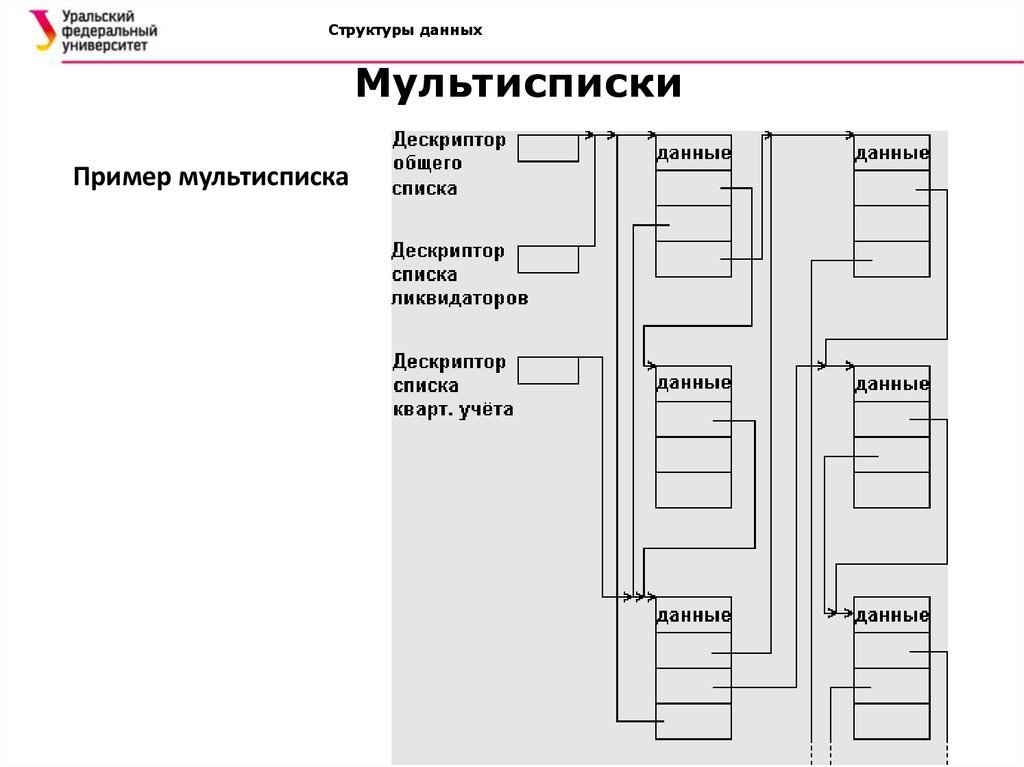
Структуры данных
Мультисписки
Пример мультисписка

65.

Структуры данных
Мультисписки
Для того чтобы при выборке каждого подмножества не
выполнять полный просмотр с отсеиванием записей, в
каждую запись включаются дополнительные поля ссылок,
каждое из которых связывает в линейный список элементы
соответствующего подмножества. В результате получается
многосвязный список или мультисписок, каждый элемент
которого может входить одновременно в несколько
односвязных списков

66.

Структуры данных
Мультисписки
Специфика мультисписка проявляется только в операции
исключения элемента из списка. Исключение элемента из
какого-либо одного списка еще не означает необходимости
удаления элемента из памяти, так как элемент может
оставаться в составе других списков.

67.

Структуры данных
ДИНАМИЧЕСКИЕ СТРУКТУРЫ ДАННЫХ.
СВЯЗНЫЕ СПИСКИ
Тема 7:
Нелинейные разветвленные списки

68.

Структуры данных
Нелинейные разветвленные списки
Основные понятия
1.
2.
Нелинейным разветвленным списком является список,
элементами которого могут быть тоже списки.
Если один из указателей каждого элемента списка
задает
порядок,
обратный
к
порядку,
устанавливаемому другим указателем, то такой
двусвязный список будет линейным
Если же один из указателей задает порядок
произвольного вида, не являющийся обратным по
отношению к порядку, устанавливаемому другим
указателем, то такой список будет нелинейным.

69.

Структуры данных
Нелинейные разветвленные списки
Схематичное представление
разветвленного списка

70.

Структуры данных
Нелинейные разветвленные списки
Разветвленные списки описываются тремя
характеристиками:
порядком
глубиной
длиной.

71.

Структуры данных
Нелинейные разветвленные списки
Порядок. Над
элементами
списка задано
транзитивное
отношение,
определяемое
последовательностью, в которой элементы появляются
внутри списка. В списке (x,y,z) атом x предшествует y, а y
предшествует z. При этом подразумевается, что x
предшествует z.
Данный список не эквивалентен списку (y,z,x). При
представлении списков графическими схемами порядок
определяется
горизонтальными
стрелками.
Горизонтальные стрелки истолковываются следующим
образом:
элемент из которого исходит стрелка,
предшествует элементу, на который она указывает.

72.

Структуры данных
Нелинейные разветвленные списки
Глубина. Это максимальный уровень, приписываемый
элементам внутри списка или внутри любого подсписка в
списке. Уровень элемента предписывается вложенностью
подсписков внутри списка, т.е. числом пар круглых скобок,
окаймляющих элемент
Длина - число элементов уровня 1 в списке.

73.

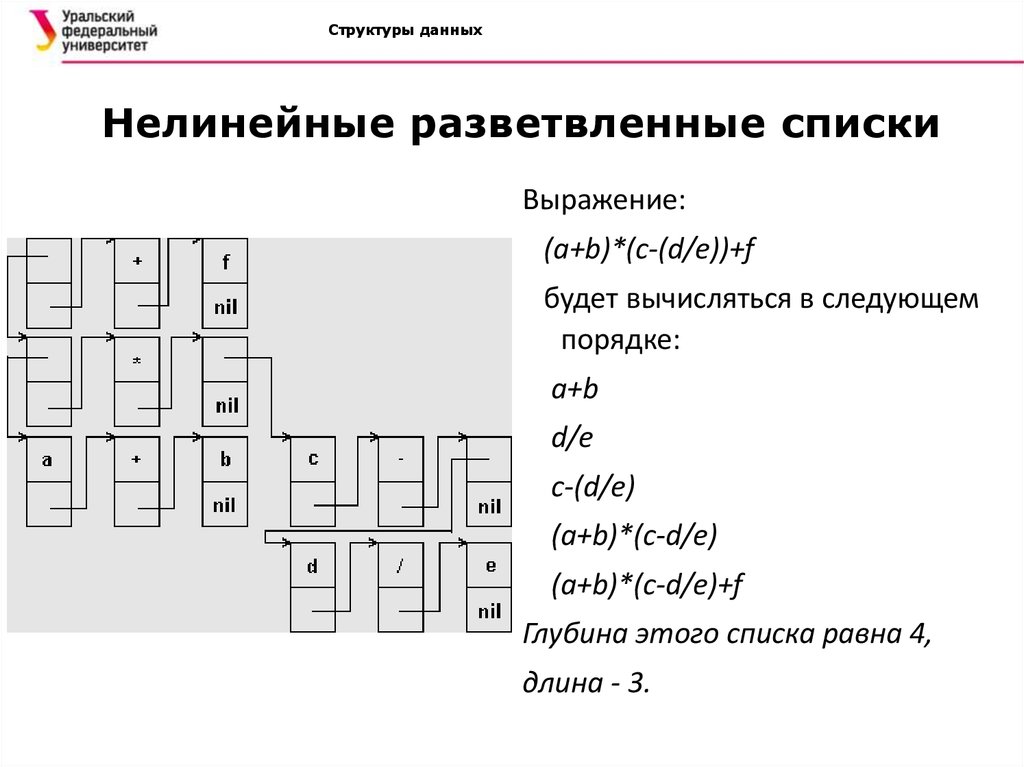
Структуры данных
Нелинейные разветвленные списки
Выражение:
(a+b)*(c-(d/e))+f
будет вычисляться в следующем
порядке:
a+b
d/e
c-(d/e)
(a+b)*(c-d/e)
(a+b)*(c-d/e)+f
Глубина этого списка равна 4,
длина - 3.

74.

Структуры данных
Нелинейные разветвленные списки
Представление списковых структур в памяти
data данные атома
down - указатель на
подсписок того же
уровня
next - указатель на
следующий элемент
Элементы списка могут быть двух видов: атомы,
содержащие данные и узлы, и содержащие указатели
на подсписки. В атомах не используется поле down
элемента списка, а в узлах - поле data. Поэтому
логичным является совмещение этих двух полей в одно:
type
data/down
next

75.

Структуры данных
Нелинейные разветвленные списки
Поле type содержат признак атом/узел, оно может
быть 1-битовым. Такой формат элемента удобен для
списков, атомарная информация которых занимает
небольшой объем памяти.
В этом случае теряется
незначительный объем памяти в элементах списка, для
которых не требуется поля data. В более общем случае
для атомарной информации необходим относительно
большой объем памяти. Наиболее распространенный в
данной ситуации формат структуры узла:
type
data/down
next

76.

Структуры данных
Нелинейные разветвленные списки
Операции обработки списков
Базовыми операциями при обработке списков являются
операции (функции):
car,
cdr,
cons
atom.

77.

Структуры данных
Нелинейные разветвленные списки
Операция car в качестве аргумента получает список
(указатель на начало списка). Ее возвращаемым
значением является первый элемент этого списка
(указатель на первый элемент). Например:
если X - список (2,6,4,7), то car(X) - атом 2;
если X - список ((1,2),6), то car(X) - список (1,2);
если X - атом то car(X) не имеет смысла и в
действительности не определено.

78.

Структуры данных
Нелинейные разветвленные списки
Операция cdr в качестве аргумента также получает
список. Ее возвращаемым значением является остаток
списка - указатель на список после удаления из него
первого элемента. Например:
если X - (2,6,4), то cdr(X) - (6,4);
если X - ((1,2),6,5), то cdr(X) - (6,5);
если список X содержит один элемент, то cdr(X) равно nil.

79.

Структуры данных
Нелинейные разветвленные списки
Операция cons имеет два аргумента: указатель на
элемент списка и указатель на список. Операция включает
аргумент-элемент в
начало аргумента-списка и
возвращает указатель
на получившийся список.
Например:
если X - 2, а Y - (6,4,7), то cons(X,Y) - (2,6,4,7);
если X - (1,2), Y - (6,4,7), то cons(X,Y) - ((1,2),6,4,7).

80.

Структуры данных
Нелинейные разветвленные списки
Операция atom выполняет проверку типа элемента
списка. Она должна возвращать логическое значение:
true - если ее аргумент является атомом, или false - если
ее аргумент является подсписком.

81.

Структуры данных
ДИНАМИЧЕСКИЕ СТРУКТУРЫ ДАННЫХ.
СВЯЗНЫЕ СПИСКИ
Тема 8:
Управление динамически выделяемой памятью

82.

Структуры данных
Управление динамически выделяемой
памятью
Динамические структуры по определению характеризуются
непостоянством и непредсказуемостью размера.
Поэтому
память под отдельные элементы таких структур выделяется в
момент,
когда они "начинают существовать" в процессе
выполнения программы, а не во время трансляции. Когда в
элементе структуры больше нет необходимости, занимаемая им
память освобождается.

83.

Структуры данных
Управление динамически выделяемой
памятью
В общем случае при распределении памяти должны
быть решены следующие вопросы:
способ учета свободной памяти;
дисциплины выделения памяти по запросу;
обеспечение утилизации освобожденной памяти.

84.

Структуры данных
Управление динамически выделяемой
памятью
Память выделяется блоками.
Блоки могут быть фиксированной или
длины.
переменной
Фиксированный размер блока гораздо удобнее для
управления: в этом случае вся доступная для
распределения память разбивается на "кадры", размер
каждого из которых равен размеру блока, и любой
свободный кадр годится для удовлетворения любого
запроса. К сожалению, лишь ограниченный круг
реальных задач может быть сведен к блокам
фиксированной длины.

85.

Структуры данных
Управление динамически выделяемой
памятью
Одной из проблем, которые должны приниматься во
внимание при управлении памятью, является проблема
фрагментации (дробления) памяти. Она заключается в
возникновении "дыр" - участков памяти, которые не могут
быть использованы. Различаются дыры внутренние и внешние.
Внутренняя дыра - неиспользуемая часть выделенного
блока, она возникает, если размер выделенного блока больше
запрошенного. Внутренние дыры характерны для выделения
памяти блоками фиксированной длины.
Внешняя дыра - свободный блок, который в принципе мог
бы быть выделен, но размер его слишком мал для
удовлетворения запроса. Внешние дыры характерны для
выделения блоками переменной длины.

86.

Структуры данных
Контрольные вопросы
1.Каковы особенности динамических структур данных?
2. Перечислите основные динамические структуры?
3. Какие основные операции выполняются над
динамическими структурами?

87.

Структуры данных
Спасибо за внимание!