12.58M

Категория:

Философия

Похожие презентации:

Суждения и высказывания

Суждение. Простые суждения и их виды

Суждение. Виды и состав суждений

Суждение. Структура суждения

Суждение. Суждение, как форма мышления

Суждение. Классификация суждений и вопросов

Логика. Суждение (Тема №3)

Суждение как форма мышления

Логика. Суждение и вопрос. (Тема 5)

Суждение. Структура суждения

Логика. Суждение. Высказывание

1.

ЛОГИКА
Тема 3.1. Суждение (высказывание)
Преподаватель –
старший преподаватель
кафедры философии и
идеологической работы
САЩЕКО РОМАН
СЕРГЕЕВИЧ

2.

1. Суждение как форма мышления.
2. Деление суждений по качеству и количеству.
3. Распределенность терминов в суждении.

Суждение как форма абстрактного мышления
1.
СУЖДЕНИЕ
Утверждение
Отрицание
Суждение (высказывание) –
форма мышления, посредством
которой утверждается наличие
или отсутствие каких-либо
связей или отношений между
предметами.
Истинность и ложность – важнейшие
характеристики суждения, отличающие
его от понятия.

4.

Суждение как форма мышления
Любое
суждение
представляет
собой
по
форме высказывание, однако эти два понятия не являются
синонимами в строгом смысле слова. Высказывание задает
существование некой общей связи между понятиями, является
способом
ее
словесного
выражения,
в
то
время
как
суждение,
кроме
самой
этой
связи
между
понятиями, указывает на ее характер.
Для различения суждений и высказываний в логике применяют
термины: суждение называют "простое высказывание", "простое
суждение", а высказывание называют "сложное высказывание",
"сложное суждение". разделение на "простые" и "сложные"
связано с тем, что высказывания (сложные) создаются из
суждений (простых) при помощи логических союзов.

5.

Суждение как форма мышления
У теории суждений (силлогистики) и теории высказываний
(логики высказываний) также разные авторы. Первая была
разработана Аристотелем, вторая - Зеноном, представителем
школы стоиков (напомним из первой лекции, ему же
принадлежит честь создания термина "логика").
Например, выражение "Если солнце садится в тучи, то завтра
будет пасмурно" - высказывание, задающее
причинноследственную связь между понятиями "заход солнца, затянутый
тучами" и "пасмурная погода". А вот выражение "Сегодня
теплее,
чем
вчера"
суждение.
Кроме
указания связи ("сегодня" является "более теплым, чем вчера")
задается ее характер ("по сравнению", сегодня "относительно"
вчера).

6.

Суждение как форма мышления
Логическое значение суждения предполагает возможность оценивать
его истинность или ложность исходя из существующего положения
дел. Однако, в логике отсутствует критерий соотнесения понятий
между собой, поэтому при оценке истинности или ложности
суждений мы вынуждены полагаться на внешние знания – научные,
здравый смысл и др. Например, суждение «Рыбы не являются
млекопитающими» мы считаем истинным исходя именно из
научных представлений, в то время как суждение «Все люди лгут»
мы считаем ложным исходя из здравого смысла.

7.

Суждение как форма мышления
Есть класс языковых выражений, которые не относятся ни к
суждениям, ни к высказываниям, т.к. они не дают возможности
оценить их как истинные или ложные. Не являются суждениями:
- вопросы, например, «Является ли свобода высшей
нравственной ценностью?»,
- повеления, например, «Откройте окно!».

8.

ЛОГИЧЕСКАЯ СТРУКТУРА СУЖДЕНИЯ:
Субъект (S) – мысль о предмете, о котором
утверждается или отрицается что-либо.
Предикат (P) – мысль о том, что именно
утверждается или отрицается в предмете.
Связка – раскрывает связь между
субъектом и предикатом.

9.

Пример: Земля является планетой.
В нем субъект S – «Земля», предикат P – « планета»,
связка – слово «является».
Философия является общеобразовательной
дисциплиной.
S «философия», предикат P – «общеобразовательная
дисциплина », связка – слово «является».
Формула суждения:
«S есть (не есть) Р»
S-Р

10.

Квантор указывает, относится ли признак,
выраженный в предикате суждения, ко всему
объему или к части объема понятия,
выражающего субъект.
Квантор находится перед субъектом и
обозначается словами: «все», «некоторые»,
«многие», «ни один» и т.д. (квантор в суждении
может и отсутствовать).
Пример: все абитуриенты сдают выпускные
экзамены и ЦТ.

11.

ПРОСТЫЕ
невозможно выделить часть,
которая была бы
самостоятельным суждением.
Пример: «я-преподаватель
философии»
СЛОЖНЫЕ
состоят из двух или более
суждений, связанных между
собой.
Пример: «Я – преподаватель
философии и я обязан
осуществлять образовательноидеолого-воспитательный
процесс»

12.

Структура простого суждения. Виды суждений.
Например "Дом (S) – это строение (Р)", где связка "есть"
грамматически пропущена. Данная структура очевидна для тех
суждений, в которых нечто явным образом утверждается или
отрицается с помощью глагола "быть", "являться".
Однако и суждения, использующие другие языковые конструкции,
также легко можно привести к данной структуре. Например,
суждение "Человек не имеет средств к существованию"
преобразуется так: "Человек (S) не является тем, кто имеет
средства к существованию (Р)". Такое суждение как "На воре и
шапка горит" можно привести к виду "Вор (S) является тем, на
ком "горит шапка" (Р)".

13.

Структура простого суждения. Виды суждений.
Простые суждения принято разделять на:
- атрибутивные,
- релятивные,
- экзистенциальные
в зависимости от характера их предиката.

14.

Структура простого суждения. Виды суждений.
Атрибутивными, или категорическими называются суждения, в
которых по отношению к предмету мысли, выражаемому субъектом,
приписывается либо отрицается некоторое свойство, или атрибут
("быть строением", нет средств).
Релятивные суждения в свою очередь описывают отношения между
несколькими предметами мысли, где некоторому субъекту
приписывается несколько предикатов.
Например, следующее: "Сосна (S) выше, чем ель (Р1), но ниже
секвойи (Р2)". Предикат, подобный данному в примере называется
"двухместный предикат" - это не сложное суждение, т.к. в признаке
речь идет об одном и том же (о высоте по отношению к предмету
мысли).

15.

Структура простого суждения. Виды суждений.
Экзистенциальные суждения не имеют явно выраженного
предиката, но утверждают или отрицают существование
предмета мысли, например "Черные дыры существуют", "Двух
мнений
быть
не
может".
Если релятивное или экзистенциальное суждение разложить на
субъектную и предикатную части, их можно свести к
атрибутивному суждению.

16.

2.
Деление суждений качеству и количеству
ПО КАЧЕСТВУ
ПО
КОЛИЧЕСТВУ

17.

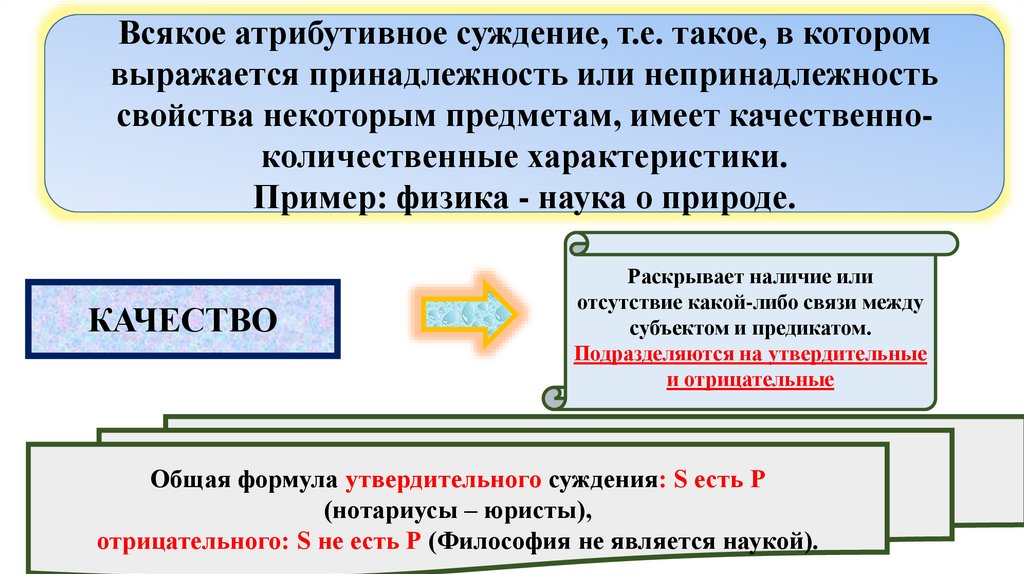
Всякое атрибутивное суждение, т.е. такое, в котором
выражается принадлежность или непринадлежность
свойства некоторым предметам, имеет качественноколичественные характеристики.
Пример: физика - наука о природе.
КАЧЕСТВО
Раскрывает наличие или
отсутствие какой-либо связи между
субъектом и предикатом.
Подразделяются на утвердительные
и отрицательные
Общая формула утвердительного суждения: S есть Р
(нотариусы – юристы),
отрицательного: S не есть Р (Философия не является наукой).

18.

КОЛИЧЕСТВО
ВЫДЕЛЯЮТ СУЖДЕНИЯ:
ЧАСТНЫЕ
ОБЩИЕ
ЕДЕНИЧНЫЕ
характеристика, раскрывающая
логический объем субъекта, т.е. когда
что-то утверждается или отрицается
либо об одном предмете, либо о части
предметов, либо о всех предметах
определенного класса.

19.

ОБЩИЕ СУЖДЕНИЯ ЧАСТНЫЕ СУЖДЕНИЯ
Суждения, в которых чтолибо утверждается или
отрицается о всех
предметах класса.
В традиционной логике
принята следующая формула
общих суждений:
все S есть Р или
ни одно S не есть Р.
Пример: все студенты академии
МВД обязаны соблюдать правила
внутреннего распорядка.
Пример: ни один человек не
может быть признан виновным в
совершении преступления, если
его вина не доказана в суде.
Суждения, в которых чтолибо утверждается или
отрицается о части какойто группы предметов.
В традиционной логике
принята следующая формула
частных суждений:
некоторые S есть (не есть) Р
Пример: некоторые студенты
академии МВД нарочно
нарушают правила внутреннего
распорядка.
Пример: некоторые преступления
совершаются не преднамеренно.
ЕДИНИЧЫЕ
СУЖДЕНИЯ
суждения, в которых чтолибо утверждается или
отрицается об отдельном
предмете мысли.
В традиционной логике
принята следующая
формула единичных
суждений:
Это S есть (не есть) Р
Пример: Эта лекция
скучная.
Пример: Этот зачет
не сложный

20.

Каждое суждение обладает определенным качеством и количеством
одновременно. Поэтому в практике мышления пользуются их объединенной
классификацией по количеству и качеству.
По этой классификации существуют четыре основных вида суждений:
Общеутвердительные
Общеотрицательные
Частноотрицательные
Частноутвердительные

21.

Общеутвердительные
(Принято обозначать
буквой «а»)
Суждения по количеству общие, а по
качеству утвердительные.
Формула: все S суть Р (SаР)
Пример: все судьи – юристы.
Все финансисты - экономисты
Общеотрицательные
Суждения по количеству общие, а по качеству
отрицательные.
Формула: ни одно S не есть Р (SеР)
Пример: ни один сфальсифицированный
документ не является доказательством.
(Принято обозначать буквой
«е»)
Частноутвердительные
(Принято обозначать буквой «i»)
Частноотрицательные
(Принято обозначать буквой
«o»)
Cуждения по количеству частные, а по
качеству утвердительные.
Формула: некоторые S суть Р (SiР)
Пример: некоторые философы –
идеалисты.
Cуждения по количеству частные, а по
качеству отрицательные.
Формула: некоторые S не есть Р (SоР)
Пример: некоторые страны Евросоюза не
являются зоной Шенгена.

22.

Качественно-количественная классификация
суждений
Обозначение с помощью латинских букв A, E, I, O - закрепленное в
логике обозначение простых суждений. Оно используется, в том
числе, и для записи суждений в составе умозаключений.
Например суждение «Все люди – разумные существа» имеет вид
«Все S есть Р», или SaP. Точно также формулы SiP, SeP, SoP
обозначают
соответственно
частноутвердительные,
общеотрицательные и частноотрицательные суждения.
Кроме того, запись "ЕIO" означает, что перед нами умозаключение,
посылки
которого
общеотрицательное
(Е)
и
частноутвердительное
(I)
суждения,
а
вывод
частноотрицательный (O).

23.

Качественно-количественная классификация
суждений
Эти буквы взяты из двух латинских слов:
"АffIrmo" (букв., "утверждаю"). "А" стоит в начале слова и как бы
указывает "утверждаю обо всем", "I" стоит ровно в середине
слова и как бы говорит: "утверждаю о части".
"Nego" (букв., "отрицаю"). По аналогии с предыдущим словом,
взяты первая и вторая гласные - "Е" и "О".

24.

Вопрос 3. Распределенность терминов в
суждении
Терминами простого суждения называют его субъект и предикат, S
и P.
Распределенность термина - это показатель его объема.
Распределенный термин взят в полном объеме (всем объемом
входит в объем второго термина или исключается из него).
Нераспределенный термин взят в части объема (частично входит в
объем
второго
термина
или
исключается
из
него). Распределенный термин обозначается знаком "+",
нераспределенный - знаком "-".

25.

Распределенность терминов простого суждения
Распределенность объемов - это константа. Распределенность
терминов показывает их взаимные логические отношения. Так,
например, В обычном общеутвердительном суждении S подчинен
P, является его частным случаем. Тогда "S" взят в полном объеме,
распределен, или обозначен "+", а "P" - взят в части объема
(только часть носителей признака принадлежат к группе
субъекта), он нераспределен, или обозначен знаком "-".

26.

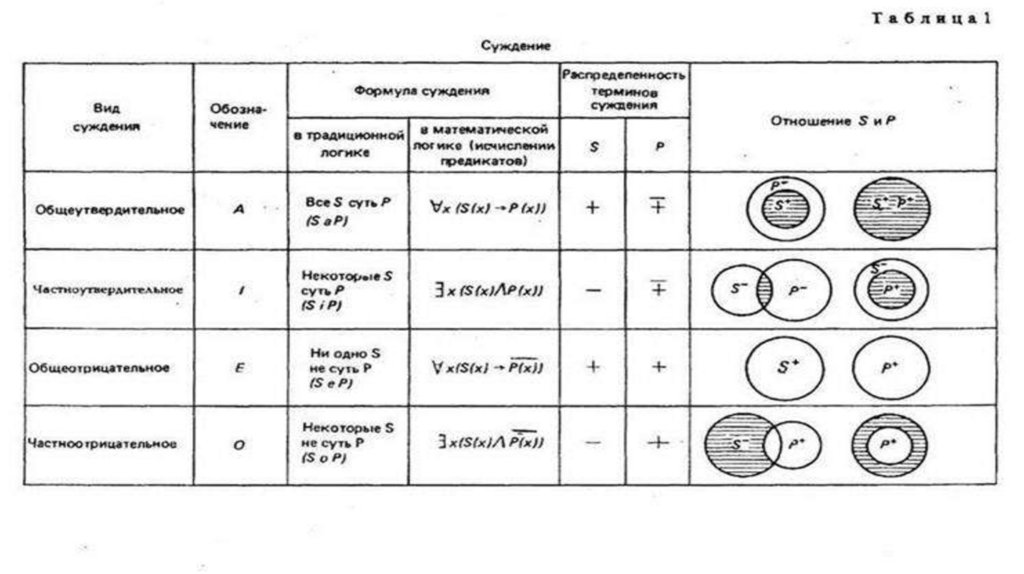
Распределенность терминов простого суждения
В таблице отношения между терминами в простом суждении
показаны на схемах Эйлера-Венна. Других отношений между
терминами простого суждения быть не может.
Столбик с математической записью формул можно пропустить,
хотя он тоже чрезвычайно интересен и хорош.

27.

Распределенность терминов простого суждения

28.

ЛОГИКА ПРЕДИКАТОВ или КВАНТОРНАЯ ЛОГИКА
является расширением ЛОГИКИ СУЖДЕНИЙ за счет
двух кванторных символов:
∀ (alle [але]) – «все»;
∃ (existieren [экзистирен]) – «существовать».
∀ - квантор всеобщности;
∃ - квантор существования
Логические связки, используемые в суждениях, в зависимости от
выражаемого ими логического смысла делятся на пять групп. Этим
группам соответствуют пять логических операций над суждениями в ЛС:
1) отрицание; 2) конъюнкция; 3) дизъюнкция (нестрогая и строгая);
4) импликация; 5) эквиваленция.

29.

КОЛ.
КАЧ.
О
У
ОБЩЕУТВЕРДИТЕЛЬНЫЕ (А)
Общие по количеству и утвердительные по качеству.
Имеют структуру: «Все S есть P».
На языке логики предикатов
суждение А
записывается:
∀х (S(x)→Р(х))
читается:
«всякий х обладает свойством Р».
Например. «Все знаки европейского гороскопа делят
год на двенадцать астрологических месяцев».

30.

КОЛ.
О
КАЧ. ОБЩЕОТРИЦАТЕЛЬНЫЕ СУЖДЕНИЯ (Е)
О
Общие по количеству и отрицательные по качеству.
Имеют структуру: «Ни одно S не-есть P».
На языке логики предикатов
суждение Е
записывается:
∀х (S(x)→ Р(х))
читается:
«ни одно х не обладает свойством Р».
Например. «Ни один студент не знает все иностранные
языки»

31.

КОЛ. КАЧ. ЧАСТНОУТВЕРДИТЕЛЬНЫЕ СУЖДЕНИЯ (I)
Ч
У Частные по количеству и утвердительные по качеству.
Имеют структуру: «Некоторые S есть P».
На языке логики предикатов
суждение I
записывается:
∃х (S(x)& Р(х))
читается:
«существуют такие х, которые обладают свойством Р».
Например. «Некоторые лекарственные растения растут на
территории Беларуси».

32.

КОЛ. КАЧ. ЧАСТНООТРИЦАТЕЛЬНЫЕ СУЖДЕНИЯ (О)
Ч
О Частные по количеству и отрицательные по качеству.
Имеют структуру: «Некоторые S не-есть P».
На языке логики предикатов
суждение О
записывается:
∃х (S(x)& Р(х))
читается:
«существуют такие х, которые не обладают свойством Р».
Например. «Некоторые
символической записи»
законы
логики
не
имеют

33.

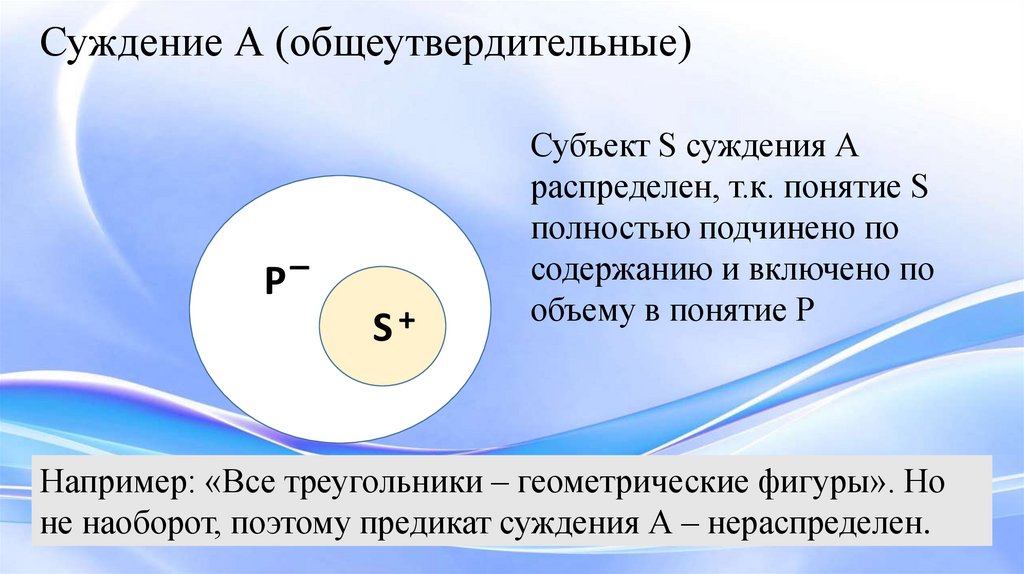
Суждение А (общеутвердительные)
Р
_
SS
S+
Субъект S суждения А
распределен, т.к. понятие S
полностью подчинено по
содержанию и включено по
объему в понятие Р
Например: «Все треугольники – геометрические фигуры». Но
не наоборот, поэтому предикат суждения А – нераспределен.

34.

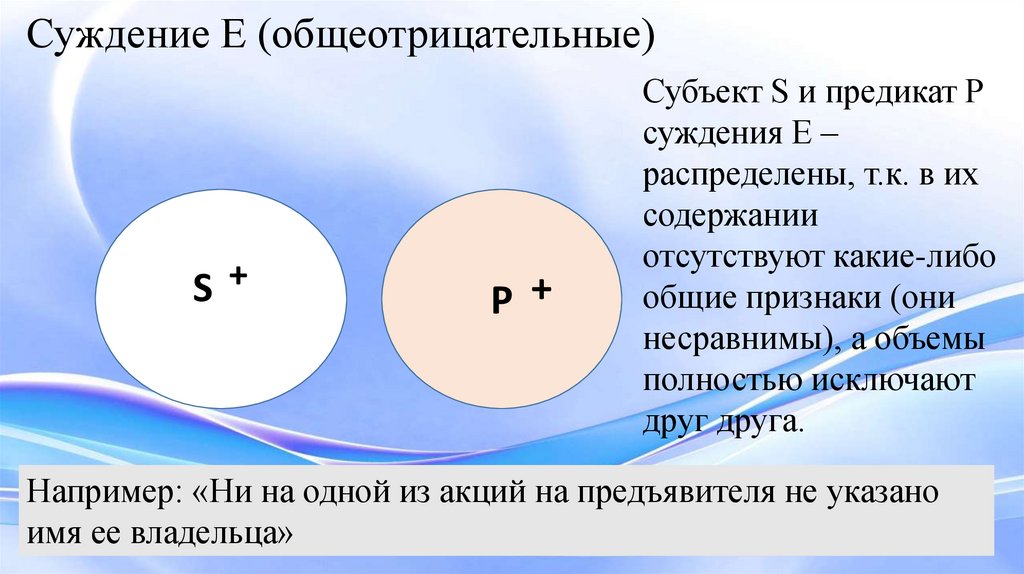
Суждение Е (общеотрицательные)
SS+
P +
Субъект S и предикат Р
суждения Е –
распределены, т.к. в их
содержании
отсутствуют какие-либо
общие признаки (они
несравнимы), а объемы
полностью исключают
друг друга.
Например: «Ни на одной из акций на предъявителя не указано
имя ее владельца»

35.

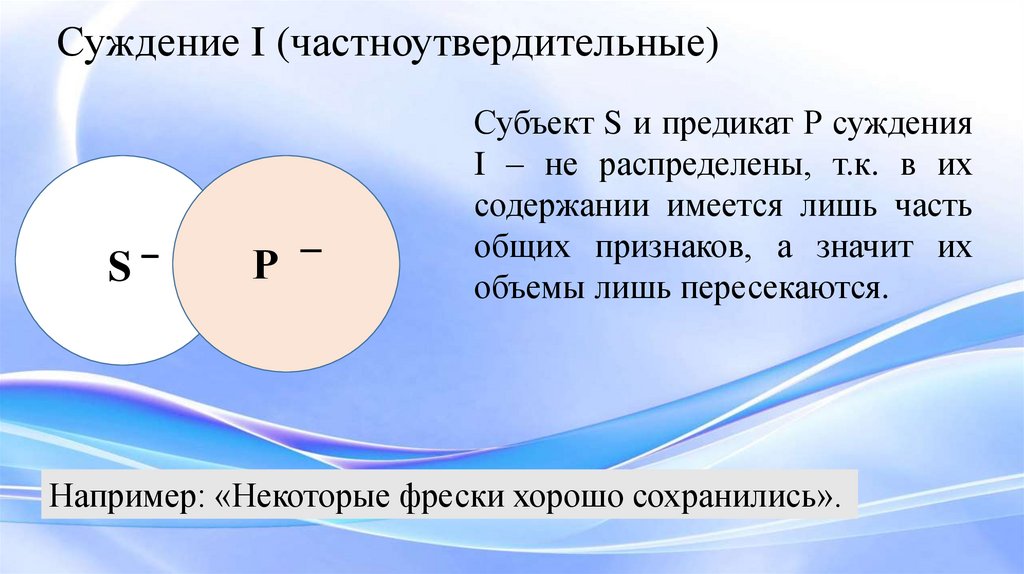
Суждение I (частноутвердительные)
S
_
Р
_
Субъект S и предикат Р суждения
I – не распределены, т.к. в их
содержании имеется лишь часть
общих признаков, а значит их
объемы лишь пересекаются.
Например: «Некоторые фрески хорошо сохранились».

36.

Суждение О (частноотрицательные)
_
S
S
Р +
Субъект S суждения О – не
распределен, т.к. значительная часть
его содержания отличается от
содержания понятия Р, который
является распределенным.
Например: «Некоторые науки не являются гуманитарными».

37.

ЛОГИКА
Тема 3.2. Суждение (высказывание)
Преподаватель –
старший преподаватель
кафедры философии и
идеологической работы
САЩЕКО РОМАН
СЕРГЕЕВИЧ

38.

Вопросы 3.2:
1. Конъюнктивные и дизъюнктивные суждения.
2. Условные и эквивалентные суждения.
3. Отношения между суждениями. Логический
квадрат.

39.

1. Конъюнктивные
дизъюнктивные
суждения.
и

40.

Конъюнктивное
(соединительное)
суждение
–
суждение, обе части которого
связаны соединительным союзом
«и».
Формула: A ʌ B
Пример: «Никто не забыт, и
ничто не забыто».

41.

Если конъюнкция выражена
простым
распространенным
предложением, то она может иметь
три исходных структуры:
Один субъект и два предиката
S есть (не есть) Р1 и Р2
Пример: «Все равны перед
законом и судом».

42.

Два субъекта и один предикат
«S1 и S2 есть (не есть) Р»
Пример: «Государственные пенсии и
социальные пособия устанавливаются законом».

43.

Два субъекта и два предиката
«S1 и S2 есть (не есть) Р1 и Р2»
Пример: «Основные права и свободы человека
неотчуждаемы и принадлежат каждому от
рождения».

44.

Дизъюнктивные
(разделительные)
суждения
–
сложные
суждения,
которые
образованы из простых путем
соединения их логическим союзом
«или» или союзом «либо».
Существует два вида дизъюнкции:
Слабая
Сильная

45.

Слабая
дизъюнкция
–
объединяемые
суждения
не
исключают друг друга.
A ˅ B (A или В)
Пример: «Гражданин Республики
Беларусь не может быть лишен
своего гражданства или права
изменить его».

46.

Сильная
дизъюнкция
–
объединяемые
суждения
исключают друг друга.
A ⊻ B (A либо В)
Пример:
право
может
способствовать
экономическому
развитию либо препятствовать ему.

47.

2.
Условные
эквивалентные
суждения.
и

48.

Условное суждение – сложное
суждение, образованное из двух
простых суждений, находящихся в
отношении основания и следствия.
Части условного суждения
соединяются
посредством
логического союза «если .... то».

49.

Пример: «Если приговор не
обоснован,
то
он
является
незаконным».
«Если приговор не обоснован» –
основание.
«То он является незаконным» –
следствие.

50.

A→B – схема условного
суждения.
A – основание.
B – следствие.
Пример: «Кто не работает, тот не
ест» – союз «если....то» отсутствует, но
подразумевается.

51.

Эквивалентное суждение –
суждение, обе части которого в
равной мере могут быть как
основанием, так и следствием.
A↔B

52.

Пример: «Если и только если человек
достиг пенсионного возраста, то он имеет
право на получение пенсии по возрасту».
(A ↔ B)
A→B – если человек достиг
пенсионного возраста, то он имеет право
на пенсию.
B→A – если человек имеет право на
пенсию, то он достиг пенсионного
возраста.

53.

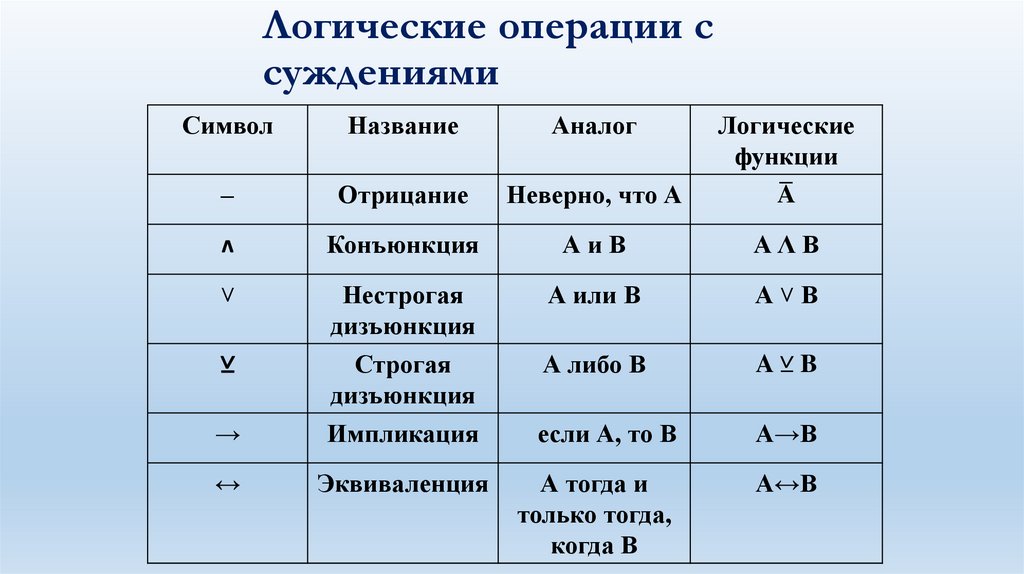
Логические операции с
суждениями:
Отрицание
Конъюнкция
Нестрогая дизъюнкция
Строгая дизъюнкция
Импликация
Эквиваленция

54.

Отрицание
–
логическая
операция,
которая
каждому
простому суждению ставит в
соответствие
суждение,
заключающееся
в
том,
что
исходное суждение отрицается.
Пример: директор фирмы –
взяточник,
директор фирмы – не взяточник.

55.

Логические операции с
суждениями
Символ
Название
Аналог
–
Отрицание
Неверно, что А
Логические
функции
–
A
ʌ
Конъюнкция
АиВ
АΛВ
˅
Нестрогая
дизъюнкция
А или В
А˅В
⊻
Строгая
дизъюнкция
А либо В
A⊻B
→
Импликация
если А, то В
А→В
↔
Эквиваленция
А тогда и
только тогда,
когда В
А↔В

56.

3.
Отношения
между
суждениями.
Логический
квадрат.

57.

Отношения между простыми суждениями. Логический
квадрат
Процесс коммуникации строится не только на сравнении понятий
(например, на кругах Эйлера), но и на сравнении суждений.
Оценками суждения являются два логических значения: истина и
ложь. Согласие или несогласие с каким-либо суждением — это
признание его истинности или ложности.

58.

Между суждениями, так же как и
между
понятиями,
существуют
определенные логические отношения.
Суждения могут быть:
сравнимые
несравнимые
совместимые
несовместимые

59.

Сравнимые суждения имеют
одинаковые субъект (S) и предикат
(Р), которые могут различаться по
количеству и качеству.
Эти суждения сопоставимы по
истинности и ложности.
Пример: некоторые подозреваемые
не правдивы.
Пример:
все
подозреваемые
правдивы.

60.

У несравнимых суждений различны
субъект (S) или предикат (Р) или то и другое
вместе.
В подобных случаях истинность или
ложность
одного
из
суждений
непосредственно не зависит от истинности
или ложности другого. Истинность или
ложность прямо определяется отношением к
действительности – соответствием или
несоответствием ей.
Пример: 1) dura legis (закон суров)
2) мирный атом

61.

Сравнимые суждения могут быть
совместимыми и несовместимыми.
Совместимыми
являются
те
суждения, которые одновременно
могут быть истинными.
Несовместимыми
являются
суждения, которые одновременно не
могут быть истинными.

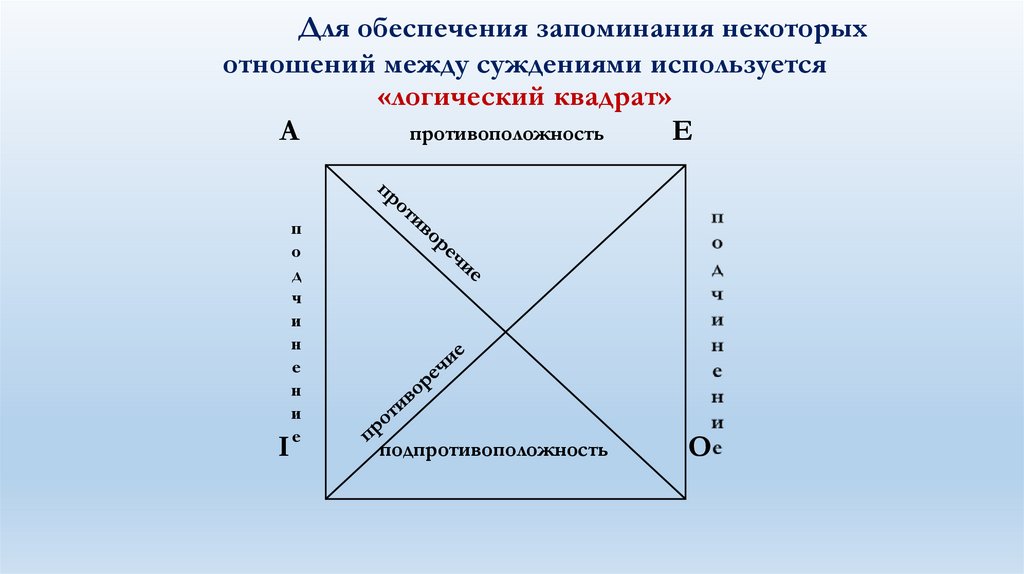
62.

Для обеспечения запоминания некоторых
отношений между суждениями используется
«логический квадрат»
А
противоположность
Е
I
п
о
д
ч
и
н
е
н
и
е
подпротивоположность
О

63.

Каждая линия на этом квадрате
изображает определенное отношение
между двумя видами суждений.
Так, суждения А – О, Е – I являются
противоречащими. Они не могут быть
одновременно истинными и ложными;
если одно из них истинно, то другое
ложно.
Пример: А (все люди смертны) – О
(некоторые люди не являются смертными).

64.

Противоположные суждения (А, Е),
в отличие от противоречащих, могут
вместе быть ложными, но не могут быть
вместе истинными.
Пример: А (все курсанты – отличники),
Е (ни один курсант не отличник).
Подпротивоположные
суждения
(I, О) не могут быть одновременно
ложными, но могут быть одновременно
истинными.

65.

Обобщенная таблица истинности
сравнимых суждений
Виды
суждений
Если истинно
А, то Е, то
I, то
Если ложно
О, то А, то Е, то
I, то
О, то
А
-
Л
?
Л
-
?
Л
И
Е
Л
-
Л
?
?
-
И
Л
I
И
Л
-
?
?
И
-
И
О
Л
И
?
-
И
?
И
-
И – истинно, Л – ложно, ? – неопределенность (истинно или ложно)

66.

Закон логики суждений – это
схема (логическая форма), которой
присуще следующее свойство:
каким бы содержимым мы ее не
наполняли, в результате получим
верное, правильное рассуждение.

67.

Закон тождества
Всякое
суждение
является
эквивалентным (тождественным) самому
себе,
следовательно,
в
правильном
рассуждении оно согласуется с самим собой.
Его форма: А А
Пример: «на войне как на войне»

68.

Закон исключенного третьего
Согласно
данному
закону
два
противоречащих суждения не могут быть вместе
ложными. Выполняется одна из возможностей:
если ложно одно из противоречащих суждений,
то истинно другое, а что-либо третье исключено.
Его форма: А v¬ А
Пример: А – суждение «Франциск Скорина
жил в Минске». Сложное суждение «Франциск
Скорина жил или не жил в Минске» – оно
истинно.

69.

Закон противоречия
В
соответствии
с
законом
противоречия
два
противоречащих
суждения не могут быть вместе
истинными, одно из них ложно.
Его форма: ¬(А v ¬А)
Пример: «Неверно, что Франциск
Скорина жил и не жил в Минске».

70.

Закон удаления двойного
отрицания
Если отрицать дважды некоторое суждение,
то в результате получается, что утверждается это
суждение без всякого отрицания.
Его форма: ¬¬ А А
Пример: «Неверно, что Иванов не виноват». Тем
самым утверждается, что Иванов виноват.
Приемлемо и обратное положение:
А ¬¬ А (закон введения двойного отрицания).

71.

Под модальностью в формальной логике
понимают выраженную в суждении дополнительную
оценочную информацию о связях между явлениями, о
логическом
статусе
суждения,
о
регулятивных,
временных и других его характеристиках.
В модальном суждении явно или неявно
используется
модальный
оператор:
«возможно»,
«необходимо», «доказано», «плохо», «запрещено» и т.д.
Пример: «Плохо, когда студент пропускает занятия по
неуважительной причине».
Структура этого суждения: М (S есть Р).
В широком смысле слова любая дополнительная
информация в суждении называется модальностью
данного суждения.

72.

1. Укажите структурные элементы
суждения:
1) объем и содержание;
2) субъект, предикат и связка;
3) посылка и заключение.

73.

2. Укажите, какими бывают суждения:
1) атрибутивными;
2) относительными;
3) нулевыми;
4) абсолютными;
5) конкретными;
6) абстрактными.

74.

3. Укажите, сколько видов суждений
включает объединенная классификация
суждений, объединяющая качественный и
количественный признаки:
• 1) 4 вида суждений;
• 2) 6 видов суждений;
• 3) 8 видов суждений;
• 4) 10 видов суждений

75.

4. «Некоторые S не есть Р» - это структура
суждений:
1) общих по количеству и утвердительных по
качеству;
2) частных по количеству и отрицательных
по качеству;
3) общих по количеству и отрицательных по
качеству;
4) частных по количеству и утвердительных
по качеству

76.

• 5. На языке логики предикатов суждений
«Ни один дельфин не живет на суше»
записывается так:
• 1) ∃х (S(x)& ˥Р(х))
• 2) ∀х (S(x)→ ˥Р(х))
• 3) ∃х (S(x)& Р(х))
• 4) ∀х (S(x)→ Р(х))

77.

6. В суждении «Некоторые люди, изучающие
логику, являются студентами»:
1)субъект распределен, предикат не
распределен;
2) субъект и предикат распределены;
3) субъект и предикат не распределены;
4) субъект не распределен, предикат
распределен

78.

7.Укажите, в каком из приведенных ниже
суждений субъект и предикат не
распределен:
1) Не все птицы – водоплавающие;
2) Все калькуляторы – вычислительные
устройства;
3) Значительную часть Земли занимают
океаны;
4) Ни одно млекопитающее не является
беспозвоночным.

79.

8. Укажите, в каком из приведенных ниже
суждений субъект распределен, а предикат не
распределен:
1) Не все птицы – водоплавающие;
2) Все калькуляторы – вычислительные
устройства;
3) Значительную часть Земли занимают
океаны;
4) Ни одно млекопитающее не является
беспозвоночным.