Двоичная система счисления

1.

Двоичная система счисления
Выполнил:
учитель информатики и ИКТ школы №473
Захаров Илья Николаевич

2.

Ей было 1100 лет,
Она в 101 класс ходила,
В портфеле по 100 книг носила —
Всё это правда, а не бред,
Когда пыля 10 ног,
Она шагала по дороге,
За ней всегда бежал щенок
С одним хвостом, зато стоногий.
Она ловила каждый звук
Своими 10 ушами.
И 10 загорелых рук
Портфель и поводок держали.
И 10 тёмно-синих глаз
Рассматривали мир привычно,
Но станет всё совсем обычным,
Когда поймёте наш рассказ.

3.

Двоичная система счисления — это
позиционная система счисления с
основанием 2.

4.

Двоичная система удобна для
компьютера, но неудобна для
человека: числа получаются
очень длинными и их трудно
записывать и запоминать.
Она используется, как правило,
для «внутренних нужд»
компьютера.
100000101001000000010
010010001010010001001

5.

«Вычисление с помощью двоек... является
для науки основным и порождает новые
открытия... При сведении чисел к
простейшим началам, каковы 0 и 1, везде
появляется чудесный порядок».
Г.В. Лейбниц
1646–1716 гг.

6.

Для записи чисел в двоичной системе
счисления используются только две цифры:
01

7.

Для целых двоичных чисел можно записать:
an−1an−2...a1a0=an−1⋅2n−1+an−2⋅2n−2+...+a0⋅20

8.

Алгоритм замещения для перевода
чисел из десятичной системы
счисления в двоичную
1. Делим десятичное число А на 2. Частное q
запоминаем для следующего шага, а
остаток a записываем как младший бит двоичного
числа.
2. Если частное q не равно 0, принимаем его за
новое делимое и повторяем процедуру,
описанную в шаге 1. Каждый новый остаток
(0 или 1) записывается в разряды двоичного числа
в направлении от младшего бита к старшему.
3. Алгоритм продолжается до тех пор, пока в
результате выполнения шагов 1 и 2 не получится
частное q= 0 и остаток a = 1.

9.

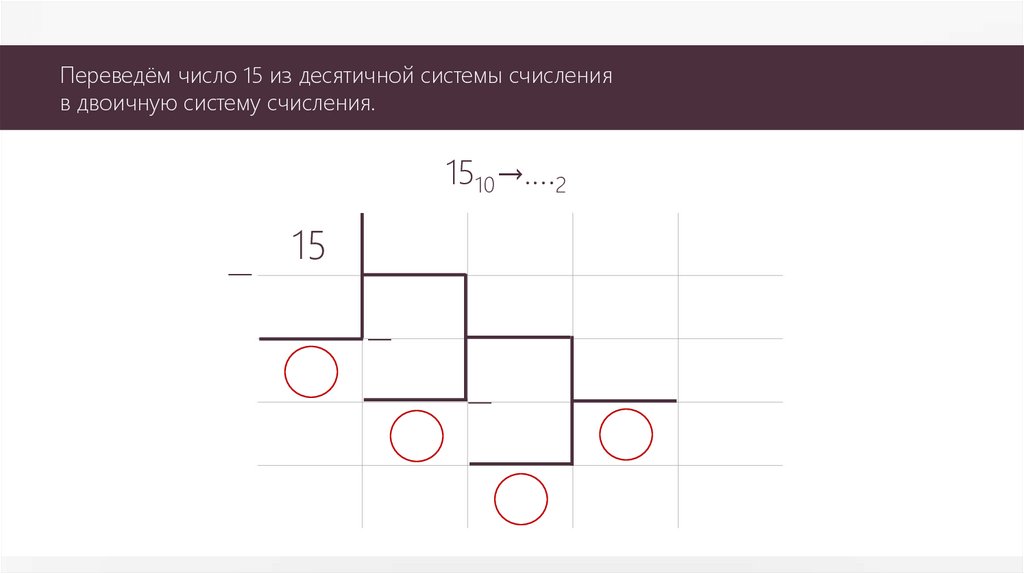
Переведём число 15 из десятичной системы счисления
в двоичную систему счисления.
1510→….2
15
2
14
7
2
1
6
3
2
1
2
1
1

10.

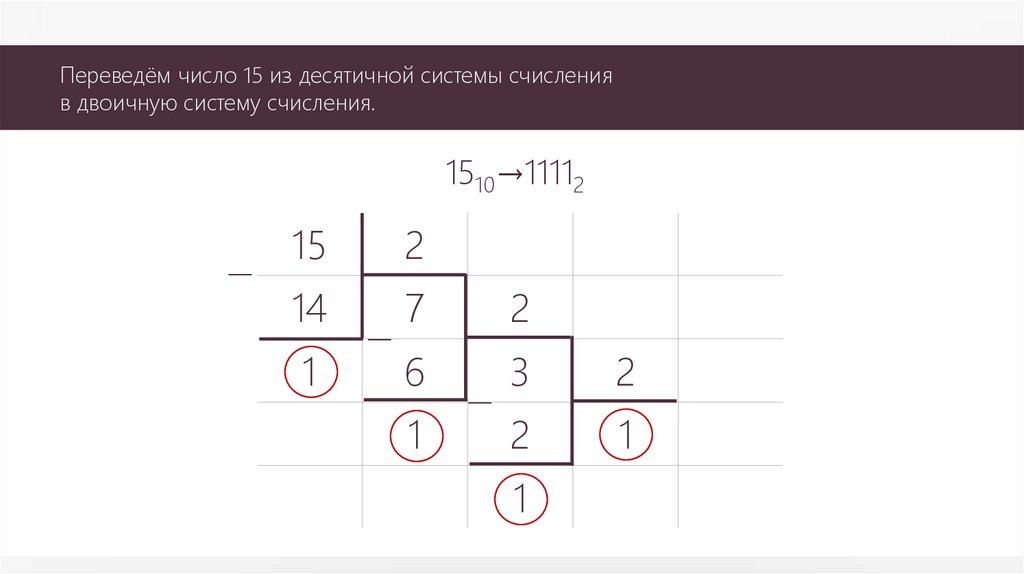
Переведём число 15 из десятичной системы счисления
в двоичную систему счисления.
1510→11112
15
2
14
7
2
1
6
3
2
1
2
1
1

11.

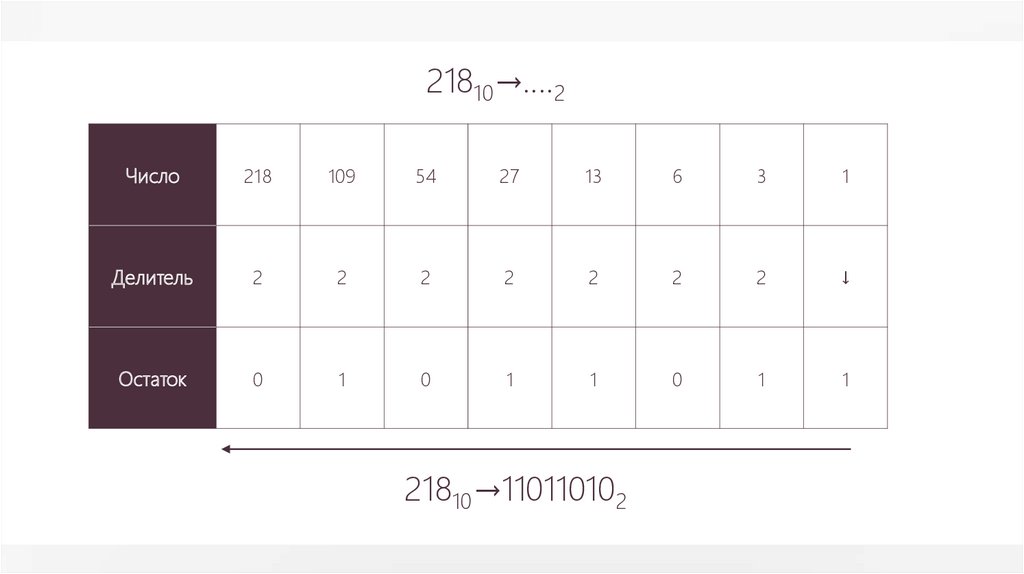
21810→….2
Число
218
109
54
27
13
6
3
1
Делитель
2
2
2
2
2
2
2
↓
Остаток
0
1
0
1
1
0
1
1
21810→110110102

12.

Правило перевода двоичного числа
в десятичное число
Для перевода двоичного числа в
десятичное необходимо это число
представить в виде суммы произведений
степеней основания двоичной системы
счисления на соответствующие цифры в
разрядах двоичного числа.

13.

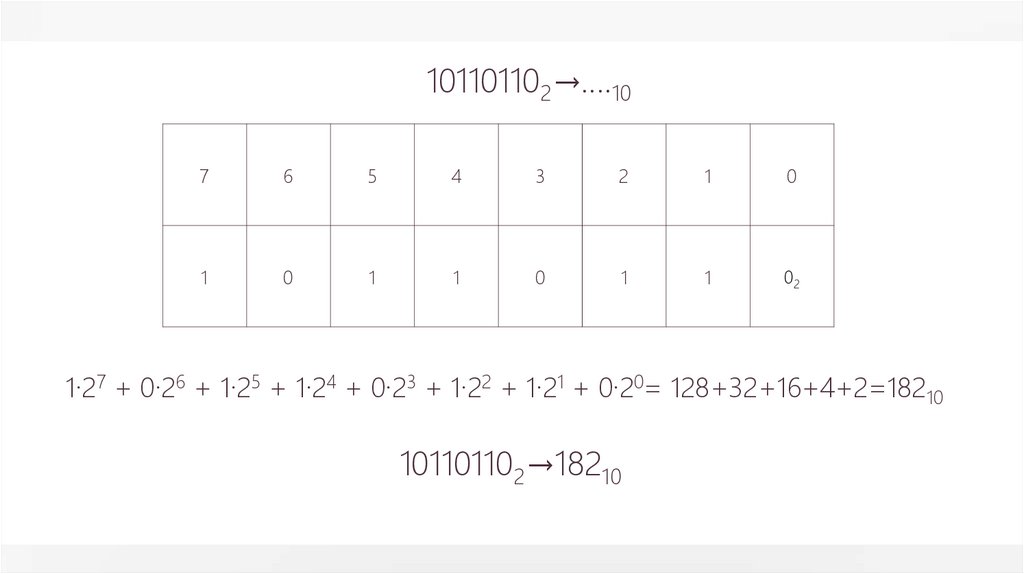
101101102→….10
7
6
5
4
3
2
1
0
1
0
1
1
0
1
1
02
1·27 + 0·26 + 1·25 + 1·24 + 0·23 + 1·22 + 1·21 + 0·20= 128+32+16+4+2=18210
101101102→18210

14.

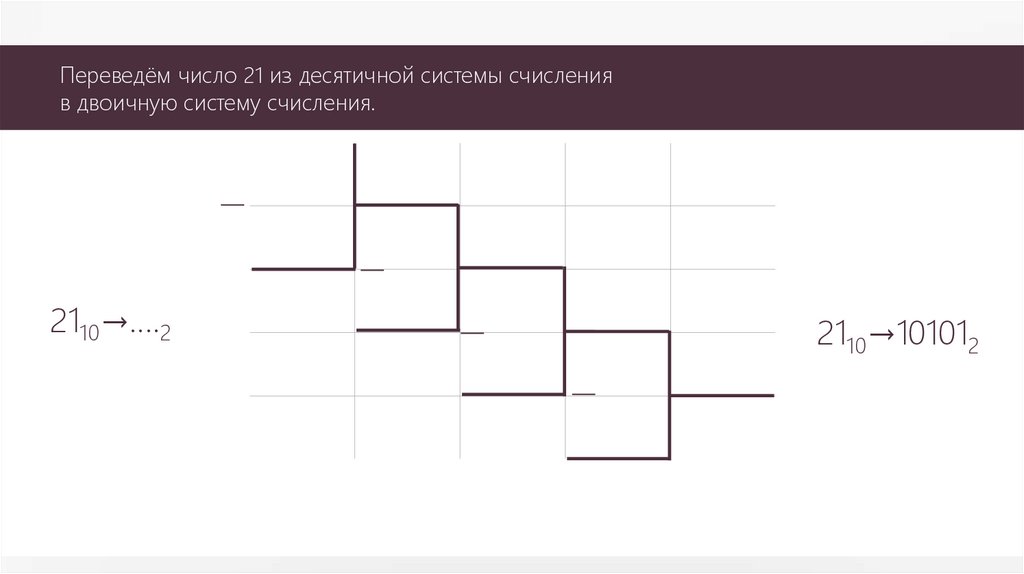
Переведём число 21 из десятичной системы счисления
в двоичную систему счисления.
2110→….2
21
2
20
10
2
1
10
5
2
0
4
2
2
1
2
1
0
2110→101012

15.

Переведём двоичное число 110011001 в десятичное.
1100110012→….10
8
7
6
5
4
3
2
1
0
1
1
0
0
1
1
0
0
12
1·28 + 1·27 + 0·26 + 0·25 + 1·24 + 1·23 + 0·22 + 0·21+1·20 = 256 + 128 + 0 +
+ 0 + 16 + 8 + 0 + 0 + 1 = 40910

16.

Переведём двоичное число 110011001 в десятичное.
1100110012→….10
8
7
6
5
4
3
2
1
0
1
1
0
0
1
1
0
0
12
1·28 + 1·27 + 0·26 + 0·25 + 1·24 + 1·23 + 0·22 + 0·21+1·20 = 256 + 128 + 0 +
+ 0 + 16 + 8 + 0 + 0 + 1 = 40910

17.

Переведём двоичное число 110011001 в десятичное.
1100110012→….10
8
7
6
5
4
3
2
1
0
1
1
0
0
1
1
0
0
12
1·28 + 1·27 + 0·26 + 0·25 + 1·24 + 1·23 + 0·22 + 0·21+1·20 = 256 + 128 + 0 +
+ 0 + 16 + 8 + 0 + 0 + 1 = 40910

18.

Переведём двоичное число 110011001 в десятичное.
1100110012→….10
8
7
6
5
4
3
2
1
0
1
1
0
0
1
1
0
0
12
1·28 + 1·27 + 0·26 + 0·25 + 1·24 + 1·23 + 0·22 + 0·21+1·20 = 256 + 128 + 0 +
+ 0 + 16 + 8 + 0 + 0 + 1 = 40910

19.

Переведём двоичное число 110011001 в десятичное.
1100110012→….10
8
7
6
5
4
3
2
1
0
1
1
0
0
1
1
0
0
12
1·28 + 1·27 + 0·26 + 0·25 + 1·24 + 1·23 + 0·22 + 0·21+1·20 = 256 + 128 + 0 +
+ 0 + 16 + 8 + 0 + 0 + 1 = 40910