Похожие презентации:
Четырехугольники. Теория
1. Геометрия 8 класс
Четырехугольники2. По страницам урока
ТеорияКонтрольные вопросы
Задачи
Это интересно
3. Путеводитель по четырехугольникам
в оглавление4. Четырехугольник
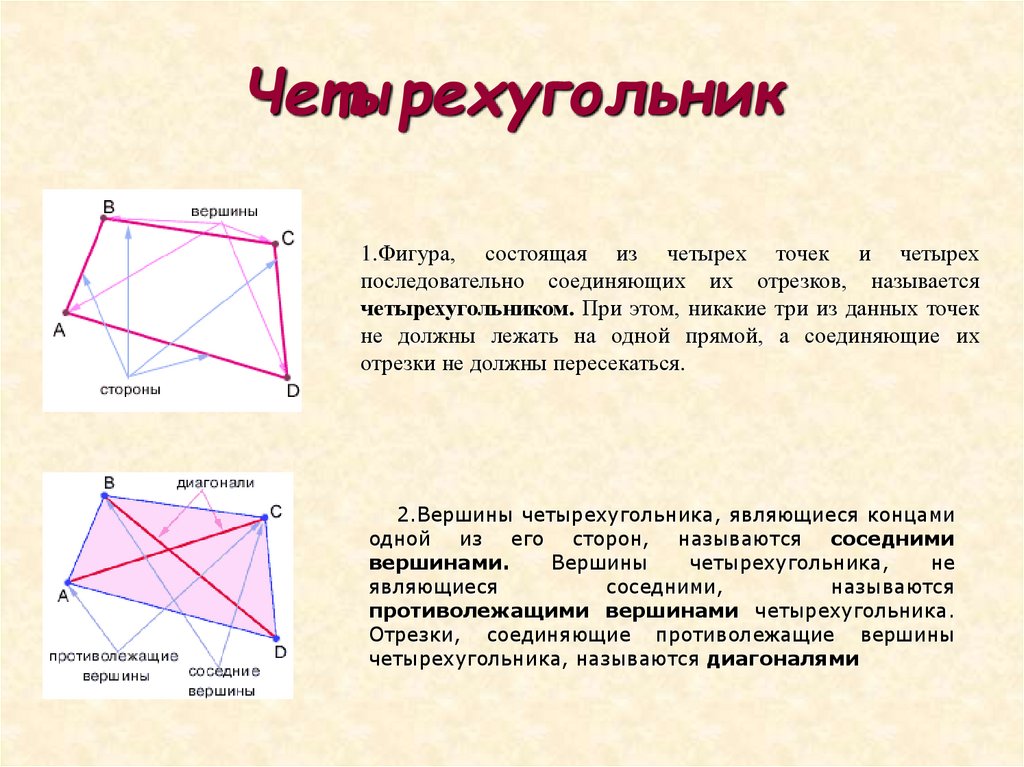
1.Фигура, состоящая из четырех точек и четырехпоследовательно соединяющих их отрезков, называется
четырехугольником. При этом, никакие три из данных точек
не должны лежать на одной прямой, а соединяющие их
отрезки не должны пересекаться.
2.Вершины четырехугольника, являющиеся концами
одной из его сторон, называются соседними
вершинами.
Вершины
четырехугольника,
не
являющиеся
соседними,
называются
противолежащими вершинами четырехугольника.
Отрезки, соединяющие противолежащие вершины
четырехугольника, называются диагоналями
5.
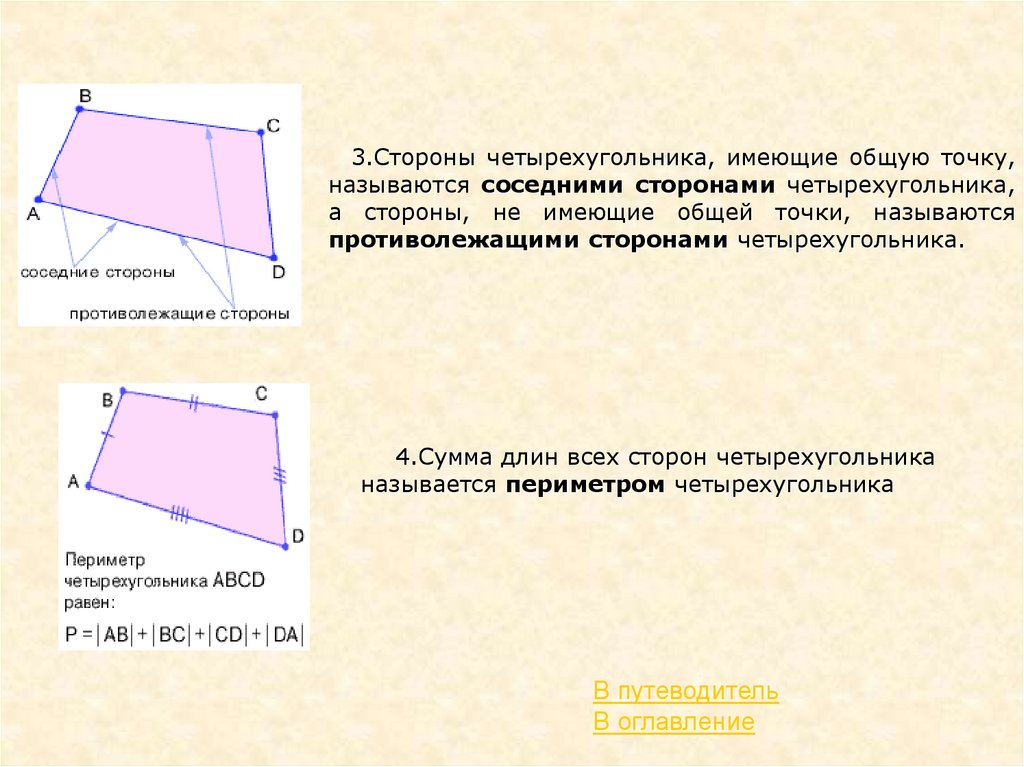
3.Стороны четырехугольника, имеющие общую точку,называются соседними сторонами четырехугольника,
а стороны, не имеющие общей точки, называются
противолежащими сторонами четырехугольника.
4.Сумма длин всех сторон четырехугольника
называется периметром четырехугольника
В путеводитель
В оглавление
6. четырехугольники
выпуклыйн
невыпуклый
н
е
7. Параллелограмм
Параллелограмм- это четырехугольник, укоторого противоположные стороны попарно
параллельны.
Свойства параллелограмма
Признаки параллелограмма
В параллелограмме
противоположные углы
равны.
Если в четырехугольнике
противоположные стороны
равны и параллельны, то это
параллелограмм.
8.
В параллелограммепротивоположные
стороны равны
Если в
четырехугольнике
противоположные
стороны равны то-это
параллелограмм
Диагонали
параллелограмма
точкой пересечения
делятся пополам
Если в
четырехугольнике
диагонали
пересекаются и точкой
пересечения делятся
пополам то-это
параллелограмм
в путеводитель
в оглавление
9. Прямоугольник
Прямоугольник- это параллелограмм, укоторого все углы прямые.
Свойства прямоугольника
Диагонали прямоугольника равны.
Все свойства параллелограмма
верны для прямоугольника.
Признак прямоугольника
Если в параллелограмме диагонали
равны, то этот параллелограммпрямоугольник.
В путеводитель
В оглавление
10. Ромб
Ромб-это параллелограмм, у которого всестороны равны.
Свойства ромба
Признаки ромба
Диагонали ромба пересекаются под
прямым углом
Если диагонали пересекаются под
прямым углом то-этот
параллелограмм-ромб
Диагональ ромба делит угол
пополам
Если диагональ делит угол пополам,
то этот параллелограмм-ромб
Все свойства параллелограмма
верны.
в путеводитель
в оглавление
11. Квадрат
Квадратом называется прямоугольник, укоторого все стороны равны.
Квадратом называется ромб, у которого все
углы прямые.
Квадрат обладает всеми свойствами ромба.
в оглавление
в путеводитель
12. Трапеция
Трапецией называется четырехугольник, укоторого две стороны параллельны, а две
другие не параллельны.
Равнобедренная
трапеция
в путеводитель
Прямоугольная
трапеция
в оглавление
13. Контрольные вопросы
Перечислите фигуры, обладающиеданными свойствами:
1. Имеют равные диагонали
2. Имеют равные противоположные углы
3. Имеют перпендикулярные диагонали
4. Имеют равные противоположные
стороны
5. Диагонали являются биссектрисами углов
◦
6. Сумма всех углов равна 360
7. Углы, прилежащие к одной стороне,
в
◦
сумме составляют угол в 180
в оглавление
далее
14. Задачи
Уровень АУровень В
Уровень С
Уровень задач
уровень А
уровеньВ
уровень С
15. Уровень А
Задача №1Дано: АВСД- параллелограмм
АЕ- биссектриса ВАД
АВ=7см,ЕС=3см
Найти периметр параллелограмма.
В
А
Задача № 2
Докажите, что параллелограмм, у которого две смежные
стороны равны, является ромбом.
Проверь себя.
Е
Д
С
16. Уровень В
Задача №1Дано:
АВСД-параллелограмм
АЕ- биссектриса ВАД
РАВСД=56 см
ВЕ:ЕС=3:1
Найти стороны параллелограмма.
В
А
Е
С
Д
Задача №2
Докажите, что четырехугольник, у которого все стороны
равны называется ромбом.
Проверь себя.
17. Уровень С
AУровень С
Задача №1
Дано:АВСД-параллелограмм;
B
C
О
D
АД=11см;CD=4cм РВОС=26см. Найти: РАOВ
Задача №2
Докажите, что биссектрисы углов
произвольного параллелограмма при
пересечении образуют
прямоугольник.
Проверь себя
18. Ответы (уровень А)
Задача №134 см.
В оглавление
В задачи
19. Ответы (уровень B)
ОтветыЗадача №1
12 см; 16 см.
В оглавление
В задачи
(уровень B)
20. Ответы (уровень С)
Задача№119см
У тебя такой
ответ?
Молодец!
В оглавление
21.
О параллелограммеТермин «параллелограмм» греческого происхождения и, согласно Проклу, был
введен Евклидом. Понятие параллелограмма и некоторые его свойства были
известны еще пифагорейцам.
В «Началах» Евклида доказывается следующая теорема: в параллелограмме
противоположные стороны равны и противоположные углы равны, а диагональ
разделяет его пополам. Евклид не упоминает о том, что точка пересечения
диагоналей параллелограмма делит их пополам.
О ромбе
Слово « ромб» тоже греческого происхождения, оно означало в древности
вращающееся тело, веретено, юлу. Произведен от греческого «бубен». Название
оправдывается тем, что ромб похож на четырехугольный бубен.
О квадрате
Термин «квадрат» происходит от латинского quadratum (quadrare- сделать
четырехугольным), перевод с греческого «тетрагонон» - четырехугольник.
О трапеции
«Трапеция» - слово греческое, означавшее в древности « столик» (по гречески «
трапедзион» означает столик, обеденный стол. Сравните трапеза, трапезная).
В «Началах» Евклида термин «трапеция» использовался для обозначения всех
четырехугольников, кроме параллелограмма.



















 Математика
Математика








