Принцип Дирихле и его применение

1. Муниципальное казенное общеобразовательное учреждение «Каменская средняя общеобразовательная школа» Индивидуальный проект Тип

проекта: информационно-познавательный
Тема проекта: «Принцип Дирихле и его
применение»
Автор проекта: Чикунова Елена,
обучающаяся 7 класса МКОУ
Наставник проекта:
Марина Сергеевна Мартова,
учитель математики
Каменский,2022

2.

Содержание
Аннотация наставника.
Введение.
1. Теоретическая часть.
1.1 Биография Дирихле.
1.2Принцип Дирихле и его формулировки.
2. Практическая часть.
2.1 Принцип Дирихле и арифметика.
2.2 Принцип Дирихле в геометрии.
2.3 Принцип Дирихле в комбинаторных задачах.
Заключение.
Список литературы.
Приложение.

3. Введение

Цель работы: изучение принципа Дирихле, применение
его в решении задач.
Задачи работы:
1. Изучить литературу по данной теме;
2. Научиться решать задачи на принцип Дирихле;
3. Рассмотреть различные формулировки принципа
Дирихле;
4. Классифицировать задачи в соответствии с их
содержанием и научиться применять изученный
принцип к решению задач;
5. Сделать буклет « Принцип Дирихле и его
применение в решении задач».

4.

5. 6. Лежён Дирихле (1805-1859)

Ввёл такое понятие, как «условная
сходимость» и определил её признак;
Доказал теорему о прогрессии;
Высказал принцип Дирихле;
Развил теорию потенциала.

7.

Формулировки принципа Дирихле
•Если в n клетках сидят (n+1) «зайцев", то есть клетка, в
которой не менее 2-х "зайцев".
•Если в n клетках сидят не более (n-1) "зайцев", то есть пустая
"клетка".
•Если в n клетках сидят не более (nk-1) "зайцев", то в какой-то
из клеток сидят не более (k-1) "зайцев".
•Если в n клетках сидят не менее (nk+1) "зайцев", то в какой-то
из клеток сидят не менее k+1 "зайцев".
•Среди p + 1 целых чисел найдутся два числа, дающие при
делении на p один и тот же остаток
•"Среди любых n + 1 целых чисел найдутся два числа таких,
что их разность делится на n"
•"Если на отрезке длины L расположено несколько отрезков с
суммой длин больше L, то хотя бы два из них имеют общую
точку".
•"Если внутри фигуры площади S находится несколько фигур,
имеющих сумму площадей больше S, то хотя бы две из них
имеют общую точку".

8.

Принцип Дирихле
Если в n клетках сидят (n+1) «зайцев", то
есть клетка, в которой не менее 2-х
"зайцев".
Если в n клетках сидят не более (n-1)
"зайцев", то есть пустая "клетка".

9.

10.

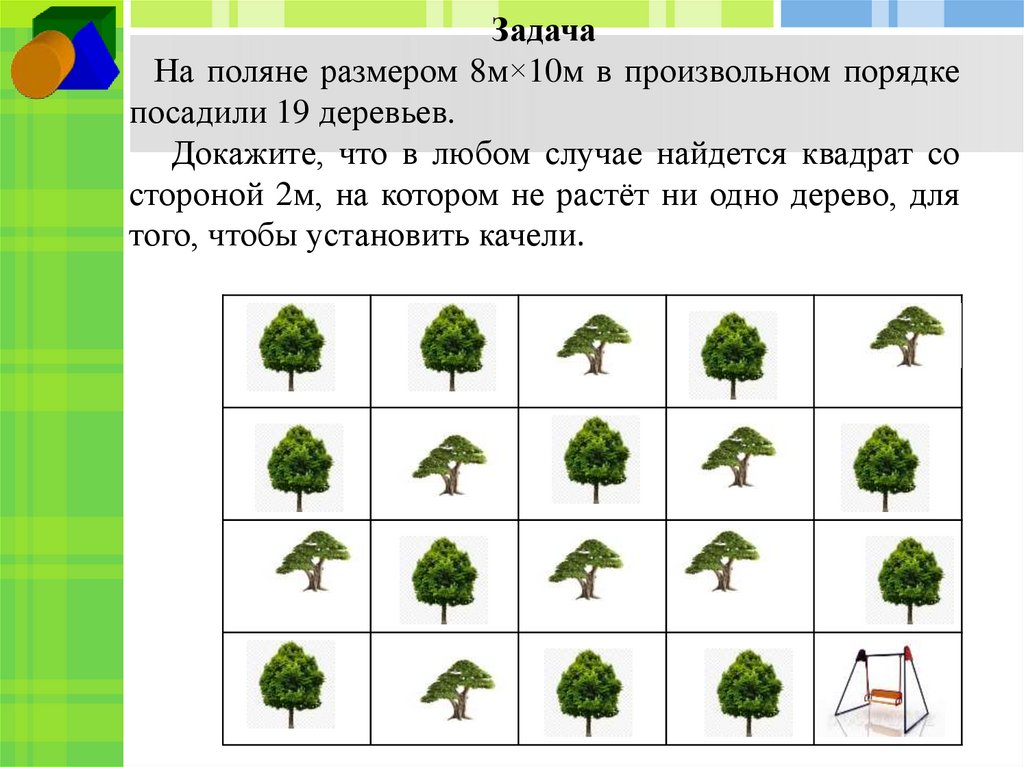
Задача
На поляне размером 8м×10м в произвольном порядке
посадили 19 деревьев.
Докажите, что в любом случае найдется квадрат со
стороной 2м, на котором не растёт ни одно дерево, для
того, чтобы установить качели.

11.

Список литературы
1. Андреев А.А., Горелов Г.Н., Люлев А.И., Савин А.Н.
Математика, Принцип Дирихле, Выпуск 1, 1997
2. Бородин А.И., Бугай А.С. Биографический словарь
деятелей в области
математики. - Киев, Радяньская школа, 1979
3. Бабинская И.Л. Задачи математических олимпиад М., Наука, 1975
4. http://logo-rai.ru/index.php/princip-dirihle
5.http://www.zaba.ru/cgi-
bin/tasks.cgi?tour=books.mk1.dirikhle

12. 13. Муниципальное казенное общеобразовательное учреждение «Каменская средняя общеобразовательная школа» Индивидуальный проект Тип

English Русский Правила