Математическая статистика

1. Математическая статистика

2.

Математическая статистика (МС) – это наука,
занимающаяся разработкой методов получения,
описания и обработки опытных данных с целью
изучения закономерностей массовых, случайных
явлений.
Установление
закономерностей,
которым
подчинены массовые случайные явления, основано
на изучении статистических данных, то есть на
результатах наблюдений.

3.

Генеральной
совокупностью
называется
совокупность значений исследуемого признака.
Общее число объектов генеральной совокупности
называется объемом генеральной совокупности N.
Выборочной
совокупностью
(выборкой)
называется совокупность случайно отобранных
объектов из генеральной совокупности.
Объем выборки обозначается n. Причем n N.

4.

Например, в партии из 1000 деталей отобрано для
обследования 100 деталей. На основе обследования 100
деталей судят о качестве деталей всей партии.
Тогда в данном примере объем генеральной совокупности
N = 1000, а объем выборки n = 100.
Выборочный метод заключается в том, что из
генеральной совокупности извлекается выборка
объема n, определяются характеристики, которые
принимаются в качестве приближенных оценок
соответствующих
характеристик
генеральной
совокупности. При n N выборочная совокупность
приближается к генеральной.

5.

Выборки подразделяют на:
1) повторная, при которой отобранный объект перед
отбором следующего возвращается в генеральную
совокупность;
2) бесповторная, при которой отобранный объект в
генеральную совокупность не возвращается.
На практике обычно пользуются бесповторным
случайным отбором.
Основным требованием к выборке является
репрезентативность (представительность) выборки.
Выборка будет репрезентативной, если каждый
объект выборки отобран случайно из генеральной
совокупности, и этом все объекты имеют одинаковую
вероятность попасть в выборку.

6. Статистическое распределение выборки

7.

Статистическое распределение выборки
Пусть
из
генеральной
совокупности
извлечена
выборка, причем
x1 наблюдалось n1 раз, x2 – n2 раз, xk – nk
k
раз. Причем
n n, где n – объем выборки.
i 1
i
Наблюдаемые значения xi называются вариантами, а
последовательность вариант, расположенная в порядке
возрастания называется вариационным рядом.
Числа наблюдений вариант ni называются частотами,
а их отношения к объему выборки называются
ni
*
относительными частотами: p i .
n

8.

Статистическим
распределением
выборки
называется перечень вариант и соответствующих им
частот:
или относительных частот:

9.

Статистическое распределение выборки может
быть задано и в виде последовательности
интервалов и соответствующих им частот или
относительных частот:
X
(xmin; x1)
(x1; x2)
(x2; x3)
…
(xk-1; xmax)
n
n1
n2
n3
…
nk
где (xi; xi-1) называется интервалом (частичным
интервалом), величина hi = xi - xi-1 длина i-го
интервала.
значения xmin, x1, x2 ,…, xk-1, xmax называются
границами интервалов.

10.

Статистическая функция распределения
Пусть nx – число наблюдений, при которых
значение наблюдаемого признака (объекта) меньше
некоторого значения Х. Тогда относительная частота
события Х < х определяется соотношением:
nx
*
Px .
n
Статистической
(эмпирической)
функцией
распределения называется функция, определяющая
для каждого значения х относительную частоту
nx
*
события Х < х, то есть F ( x) , где nx – число
n
вариант меньше Х, n – объем выборки.

11.

Статистическая (эмпирическая) функция распределения
F*(x) обладает всеми свойствами функции F(x) для
дискретной случайной величины.
1) Значения эмпирической функции распределения F*(х)
принадлежат отрезку [0; 1].
2) Функция F*(х) – неубывающая функция.
3) Если х1 – наименьшая варианта, то F*(х) =0 при х х1,
если хk – наибольшая варианта, то F*(х) =1 при х > хk.
Статистическая (эмпирическая) функция распределения
выборки служит для оценки теоретической функции
распределения генеральной совокупности.

12.

Пример. Задано распределение частот выборки.
Найти распределение относительных частот,
статистическую
функцию
распределения
и
построить ее график.
xi
2
6
12
ni
3
10
7
Решение:
Найдем относительные частоты рi*, для чего
разделим частоты на объем выборки n:
3
n ni 3 10 7 20.
i 1

13.

3
p
0,15;
20
*
1
10
p
0,5;
20
*
2
7
p
0,35.
20
*
3
Запишем распределение относительных частот:
xi
pi*
2
0,15
6
0,5
12
0,35
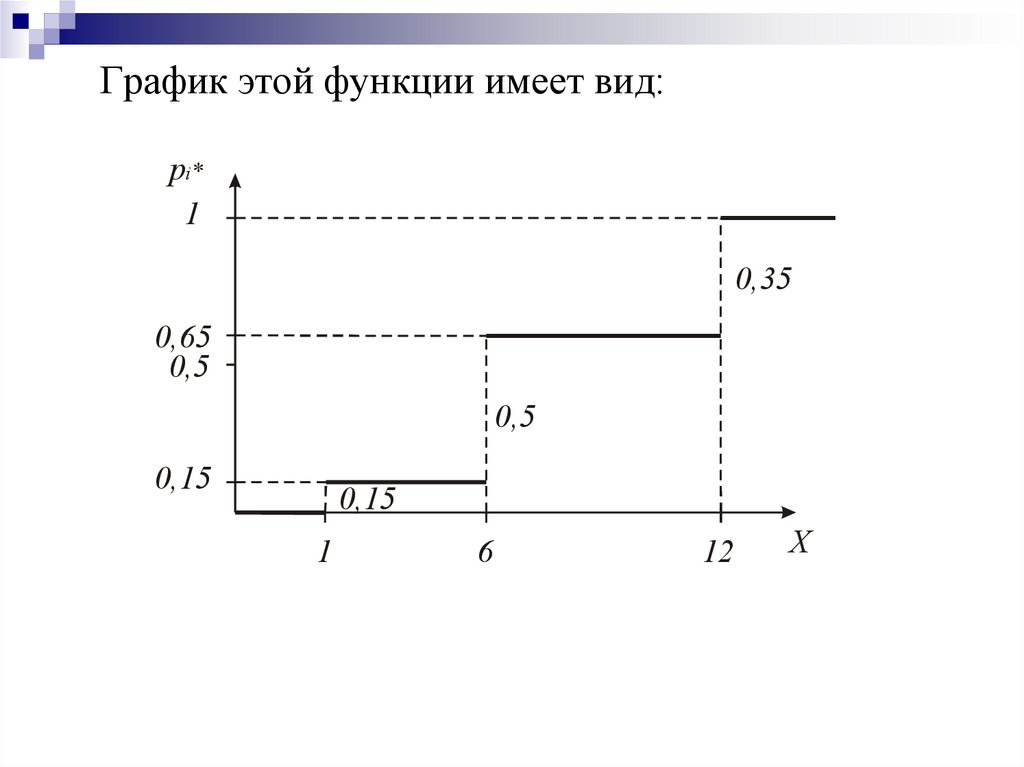
Найдем статистическую функцию распределения:
x 2;
0,
0,15, 2 x 6;
*
F ( x)
0,65, 6 x 12;
1,
x 12.

14.

График этой функции имеет вид:
pi*
1
0,35
0,65
0,5
0,5
0,15
0,15
1
6
12
X

15. Полигон и гистограмма статистического распределения

16.

Для наглядности представления статистического
распределения выборки строят различные графики. К
таким графикам относятся полигон и гистограмма.
Полигоном частот называется ломаная линия,
отрезки которой соединяют точки: (x1, n1), (x2, n2), …,
( xk, nk).
Полигоном относительных частот называется
ломаная линия, отрезки которой соединяют точки
(x1,p1*), (x2, p2*),…,( xk, pk*).

17.

Для построения полигона частот (относительных
частот) на оси абсцисс откладывают варианты xi, а
на оси ординат – соответствующие им частоты ni
(относительные частоты pi*).
ni(pi*)
n2(p2*)
n4(p4*)
n1(p1*)
n3(p3*)
x1
x2
x3
x4
X

18.

Полигон можно строить и для статистического
распределения
заданного
последовательностью
интервалов. В этом случае, в каждом интервале
выбирается одна варианта, в качестве которой могут
использоваться:
• левые границы интервалов;
• правые границы интервалов;
• середины интервалов (чаще всего).
Если величины интервалов постоянны и равны между
собой, то значения x1*, x2*, …, xk* называют
равноотстоящими вариантами.

19.

Гистограммой частот (относительных частот)
называют ступенчатую фигуру, состоящую из
прямоугольников, основаниями которых служат
частичные интервалы статистической совокупности,
представленной в виде последовательности частичных
интервалов длиною h, а высоты равны плотности
*
n
h
p
частоты i
(плотности относительной частоты i h ).
Площадь гистограммы частот равна сумме всех
частот, то есть объему выборки.
Площадь гистограммы относительных частот равна
сумме всех относительных частот, то есть единице.
Гистограмма строится, как правило, для выборки
большой размерности.

20.

Для построения гистограммы частот (относительных
частот) на оси абсцисс откладывают частичные
интервалы, а над ними проводят отрезки параллельные
*
p
оси абсцисс на расстоянии ni h ( i h ).
ni/h
xmin
x1
x2
x3
xmax
X

21.

Наглядность гистограммы зависит от числа
частичных интервалов k, определяемых по формуле:
xmax xmin
k
.
h
При этом число интервалов обычно определяется из
условия kmin 5.
На практике k часто определяется из условия k n.

22. Статистические оценки параметров распределения

23. Общие понятия статистических оценок

Пусть требуется изучить некоторый количественный
признак генеральной совокупности. Из теоретических
соображений установлен вид распределения этого
признака.
В этом случае имеет место задача оценки
неизвестных параметров известного распределения. При
этом для оценки параметров используется только
выборка значений x1, x2, …, xn, полученных в результате
наблюдений.

24.

Выборочное среднее
Пусть для изучения генеральной совокупности
относительно количественного признака Х извлечена
выборка объема n.
Выборочной
средней
называют
среднее
арифметическое
значение
признака
выборочной
совокупности.
Если все значения x1, x2, …, xn признака выборки
объема n различны,
то выборочное среднее
определяется по формуле:
1 n
xB xi ,
n i 1
где xB – выборочное среднее.

25.

Если значения признака x1, x2, …, xk имеют
соответственно частоты n1, n2, …, nk , причем
k
n ni – объем выборки, то
i 1
1 k
xB xi ni .
n i 1
Замечание: Выборочная средняя, найденная по
данным одной выборки, есть определенное число. Если
извлекать другие выборки того же объема из той же
генеральной совокупности, то выборочная средняя
будет изменяться от выборки к выборке.
Таким образом выборочную среднюю
рассматривать как случайную величину.
можно

26. Групповая и общие средние

Допустим, что все значения количественного
признака Х совокупности разбиты на несколько групп.
Рассматривая каждую группу как самостоятельную
совокупность,
можно
найти
ее
среднюю
арифметическую.
Групповой средней называют среднее арифметическое
значений признака, принадлежащих группе.
Общей средней называют среднее арифметическое
значений признака, принадлежащих всей совокупности.

27.

Зная групповые средние и объемы групп, можно
найти общую среднюю: общая средняя равна средней
арифметической групповых средних, взвешенной по
объемам групп.
Замечание: Для упрощения расчета общей средней
генеральной
совокупности
большого
объема
целесообразно разбить ее на несколько групп, найти
групповые средние и по ним общую среднюю.

28.

Пример. Найдите общую среднюю совокупности,
состоящей из двух групп:
хi
ni
1
10
6
15
хi
ni
1
20
Решение:
Найдем групповые средние:
10 1 15 6
20 1 30 5
x1
4; x2
3,4.
10 15
20 30
Найдем общую среднюю:
25 4 50 3,4
x
3,6.
25 50
5
30

29. Выборочная дисперсия

Для того, чтобы охарактеризовать рассеяние
наблюдаемых значений количественного признака
выборки вокруг среднего значения xB рассматривают
сводную характеристику – выборочную дисперсию.
Выборочной дисперсией DВ называется среднее
арифметическое квадратов отклонений наблюдаемых
значений признака от их выборочной средней.
Если все значения x1, x2, …, xn признака выборки
объема n различны, то
2
1 n
DB xi xB .
n i 1

30.

Если значения признака x1, x2, …, xk имеют
соответственно частоты n1, n2, …, nk , причем
n n1 n2
nk , то
2
1 k
DB xi xB ni .
n i 1
Таким образом, выборочная дисперсия есть средняя
взвешенная квадратов отклонений с весами, равными
соответствующим частотам.

31.

Пример. Найдите выборочную дисперсию, если
выборочная
совокупность
задана
таблицей
распределения:
хi
ni
1
20
2
15
3
10
4
5
Решение:
Найдем выборочную среднюю:
20 1 15 2 10 3 5 4 100
xB
2.
20 15 10 5
50
Найдем выборочную дисперсию:
20 (1 2) 2 15 (2 2) 2 10 (3 2) 2 5 (4 2) 2
DB
1.
50

32.

Для расчета выборочной
использовать частную формулу:
DB x 2 xB
2
или
дисперсии
можно
2
1 k
2
DB ni xi xB .
n i 1
Кроме дисперсии, для характеристики рассеяния
значений признака выборочной совокупности вокруг
своего среднего значения
пользуются сводной
характеристикой
–
средним
квадратическим
отклонением.
Выборочным средним квадратическим отклонением
(стандартом) называют квадратный корень из
выборочной дисперсии: B DB .

33.

Выборочная дисперсия DВ является состоятельной, но
смещенной оценкой D(х). Это означает, что если в
качестве
оценки
дисперсии
D(х)
генеральной
совокупности принять DВ выборочной совокупности, то
эта оценка будет приводить к систематическим ошибкам,
давая заниженное значение, так как
n 1
M ( DB )
D( x).
n
Такое смещение особенно проявляется при малых
объемах выборки. В качестве несмещенной оценки D(х)
используется исправленная дисперсия:
n
S
DB .
n 1
2

34.

n
n
2
2
n
1
1
2
S
xi xB
xi xB
n 1 n i 1
n 1 i 1
или для взвешенного статистического ряда:
k
2
1
2
.
S
x
x
n
i
B
i
n 1 i 1
Для оценки среднего квадратического отклонения
генеральной совокупности используют «исправленное»
среднее
квадратическое
отклонение,
которое
определяется по формуле:
2
1 k
.
S
x
x
n
i
B
i
n 1 i 1

35.

Замечание: Сравнивая формулы
k
1 k
1
2
2
2
DB xi xB ni и S
xi xB ni
n i 1
n 1 i 1
видим, что они отличаются только знаменателями.
Очевидно, что достаточно больших значениях n объема
выборки, выборочная и исправленная дисперсия
различаются мало.
На практике пользуются исправленной дисперсией,
если n 30.

36.

Пример. Найдите исправленную
данному распределению:
хi
ni
1
20
2
15
3
10
дисперсию
по
4
5
Решение:
Из предыдущего примера объем выборки равен 50,
выборочная средняя xB 2, выборочная дисперсия DB 1.
Определим исправленную дисперсию:
n
50
S
DB
1 1,02, S 1,02 1,01.
n 1
49
2
Так как объем выборки достаточно большой, то
исправленная дисперсия мало отличается от выборочной.

37. Характеристики вариационного ряда

Кроме выборочных средней, дисперсии и среднего
квадратического отклонения в качестве статистических
оценок вариационного ряда используются следующие
характеристики:
1. Мода М0;
2. Медиана med X;
3. Размах выборки R;
4. Среднее абсолютное отклонение θ;
5. Коэффициент вариации V.

38.

Мода М0 – варианта, имеющая наибольшую частоту
(относительную частоту).
Медиана med X – варианта, делящая вариационный
ряд на две части, равные по числу вариант.
При нечетном числе вариант (n 2l 1, l 0,1,2, )
med X xl 1
при четном числе вариант (n 2l , l 1,2,
xl xl 1
med X
2
)

39.

Размах выборки – разность между наибольшей и
наименьшей вариантами, то есть
R xmax xmin .
Среднее абсолютное отклонение – среднее
арифметическое абсолютных отклонений, то есть
1 k
xi xB ni ,
n i 1
используемое для характеристики распределения
вариационного ряда.

40.

Коэффициент вариации V – отношение выборочного
среднего квадратического отклонения к выборочному
среднему в процентах, то есть
V
в 100%
.
xв
Коэффициент вариации служит для сравнения
величин рассеяния двух вариационных рядов.
Вариационный ряд, у которого коэффициент вариации V
больше, имеет больше рассеяние.
Коэффициент вариации – безразмерная величина,
поэтому он применим для сравнения рассеяния
вариационных рядов, варианты которых имеют
различную размерность.

41.

Для оценки нормальности распределения
критерию моментов вводятся две характеристики:
Асимметрия теоретического распределения
3
3
AX 3 , где 3 M X M ( X ) ,
X
по
которая характеризует асимметричность нормального
распределения.
Если
кривая
нормального
распределения
симметрична, то АХ=0.
Если длинная часть кривой слева, то АХ<0, если
длинная часть кривой справа, то АХ>0.
Выборочная асимметрия определяется по формуле:
1 n
3
AB
x x ni .
3 i
n X i 1

42.

Эксцесс теоретического распределения
4
4
E X 4 3, где 4 M X M ( X ) 3 ( x),
X
который характеризует крутость кривой нормального
распределения.
Для кривой нормального распределения ЕХ=0.
Если кривая имеет острую вершину (вытянута), то
ЕХ>0, а если кривая пологая, то есть имеет плоскую
вершину, то ЕХ<0.
Выборочный эксцесс определяется по формуле:
1 n
4
EB
x x ni 3.
4 i
n B i 1

43.

Для
оценки
нормальности
распределения
вычисляется:
6( n 1)
Дисперсия асимметрии DА
.
(n 1)(n 3)
24n(n 2)(n 3)
.
Дисперсия эксцесса DE
2
(n 1) (n 3)(n 6)
Случайная
величина
имеет
нормальное
распределение (выполняется нулевая гипотеза), если
выполняются одновременно неравенства:
AB 3 DA ,
EB 5 DE .
Если хотя бы одно из неравенств не выполняется, то
гипотеза о нормальности распределения отвергается.

44. Интервальные оценки параметров распределения

45.

Интервальной называется статистическая оценка,
которая определяется двумя числами – концами
интервала.
Интервальные оценки позволяют определить
точность и надежность оценки статистического
параметра.
Пусть θ* – статистическая оценка неизвестного
параметра θ. Причем θ может быть как постоянной,
так и случайной величинами.
Точностью статистической оценки называется
величина , определяемая из равенства:
* .

46.

Последнее выражение показывает, чем точнее
параметр θ* описывает θ, тем меньше разность между
ними, то есть меньше величина .
В то же время статистические методы не позволяют
категорически утверждать, что оценка θ* всегда
удовлетворяет неравенству | θ– θ* | < .
Можно лишь говорить о некоторой вероятности
выполнения этого неравенства.
Надежностью
(доверительной
вероятностью)
оценки параметра θ по θ* называется вероятность или
β, с которой осуществляется неравенство
* .

47.

В соответствии с определением доверительной
вероятности можно записать, что
P * ,
тогда имеем
P( * ) , или
P( * * ) .
Последнее выражение представляет вероятность того,
что интервал (θ*– , θ*+ ) заключает в себя (покрывает)
неизвестный параметр θ.
*- *
*+
Интервал (θ*– , θ*+ ), покрывающий неизвестный
параметр θ с надежностью , называется доверительным
интервалом.

48. Доверительные интервалы для оценки математического ожидания нормального распределения при известном σ

Пусть количественный признак Х генеральной
совокупности распределен нормально, причем
среднее квадратическое отклонение σ этого
распределения известно.
Требуется оценить неизвестное математическое
ожидание а по выборочной средней x , то есть
найти доверительные интервалы, покрывающие
параметр а с заданной надежностью .

49.

Для этого необходимо, чтобы выполнялось соотношение:
P X a ,
где – заданная надежность.
Пользуясь формулой вероятности заданного отклонения
P X a 2 ,
заменив Х на X и ( X )
, получим
n
n
n
P X a 2
2 (t ), где t .
Из последнего равенства найдем t
.
n

50.

Приняв во внимание, что вероятность Р задана и равна
, окончательно получим:
P x t
a x t
2 (t ) .
n
n
где n – объем выборки, x – выборочная средняя, Ф(t) –
функция Лапласа, t – аргумент функции Лапласа,
определяемый по таблице из условия что 2Ф(t) = .
Смысл
полученного
соотношения
таков:
с
надежностью можно утверждать, что доверительный
интервал x ; x покрывает неизвестный параметр
а, с точностью оценки t .
n

51.

Пример. Случайная величина Х имеет нормальное
распределение с известным средним квадратическим
отклонением σ=3. Найти доверительные интервалы для
оценки неизвестного математического ожидания а по
выборочным средним x , если объем выборки n=36,
надежность оценки =0.95.
Решение:
Найдем t. Из соотношения 2Ф(t)=0.95 получим
Ф(t)=0.475. По таблице приложения имеем t=1.96.
Найдем точность оценки:
1.96 3
t
0.98.
n
36
Тогда доверительные интервалы: x 0.98; x 0.98 .

52.

Рассматривая различные значения выборочного
среднего, будем получать доверительные интервалы.
Например, если x 4.1 , то доверительный интервал
имеет следующие доверительные границы:
x 4.1 0.98 3.12
x 4.1 0.98 5.08
Доверительный интервал: 3.12; 5.08 .
Таким образом, значения неизвестного параметра а,
согласующиеся с данными выборки, удовлетворяют
неравенству: 3.12 a 5.08.

53.

Пример. Найти минимальный объем выборки, при
котором с надежностью 0.975, точность оценки
математического ожидания генеральной совокупности
по выборочному среднему равна 0.3, если известно
среднее квадратическое отклонение =1.2 нормально
распределенной генеральной совокупности.
Решение:
Воспользуемся формулой, определяющей точность
оценки
математического
ожидания
генеральной
совокупности по выборочной средней:
t
n
откуда
n
t 2 2
2
.

54.

По условию =0.975, следовательно,
0.975
(t )
0.4875.
2
По таблице найдем t=2.24.
Подставив в выражение, определяющее n, t=2.24,
=1.2, =0.3 найдем
(2.24) 2 (1.2) 2
n
80.2816.
2
(0.3)
Тогда искомый объем выборки n = 81.

55. Доверительные интервалы для оценки математического ожидания нормального распределения при неизвестном σ

Пусть количественный признак Х генеральной
совокупности распределен нормально, причем среднее
квадратическое отклонение σ неизвестно.
В этом случае для построения доверительного
интервала для а определяется случайная величина
(статистика Стьюдента).
( x a) n
T
,
S
где S – исправленное среднее квадратическое
отклонение.

56.

Значение случайной величины Т обозначают через t .
В этом случае можно записать, что
S
S
P x t
a x t
,
n
n
где t – табличное значение статистики Стьюдента,
определяемое по таблицам критических значений
распределения Стьюдента при известных n и .
В этом случае доверительный интервал для оценки
математического ожидания а определяется выражением:
x , x где t S .
n

57.

Пример. Количественный признак Х генеральной
совокупности распределен нормально. По
выборке
объема n=16 найдены выборочная средняя x 20.2 и
исправленное среднее квадратическое отклонение S=0.8.
Оценить неизвестное математическое ожидание при
помощи доверительного интервала с надежностью
=0.95.
Решение:
В таблице приложения по =0.95 и n=16 найдем tγ =2.13.
Найдем доверительные границы:
t S
t S
0.8
x
20.2 2.13
19.774, x
20.626.
n
16
n
С надежностью 0.95 неизвестный параметр а заключен в
доверительном интервале 19.774 a 20.626.

58.

Пример. Для определения средней урожайности
пшеницы на площади 10000 га определена средняя
урожайность на 1000 га. Результаты выборочного
исследования представлены в виде следующего
распределения
Урожайность
ц/га
Количество
гектар
11-13
13-15
15-17
17-19
150
200
450
200
Оценить с надежностью =0.95 среднюю
урожайность на всем массиве по выборочной средней
при помощи доверительного интервала.

59.

Решение:
Найдем выборочную среднюю. За значение варианты
примем середины интервалов.
12 150 14 200 16 450 18 200
x
15.4.
1000
Найдем выборочную дисперсию.
(12 15.4) 2 150 (14 15.4) 2 200
DB
1000
(16 15.4) 2 450 (18 15.4) 2 200
3.64.
1000
Так как объем выборки достаточно большой, то
заменим
S
выборочным
среднеквадратическим
отклонением D 3.64 1.91.
B
B

60.

По таблице значений статистики Стьюдента при
n>120 и = 0.95 найдем t = 1.96.
Найдем доверительные границы:
t S
1.91
x
15.4 1.96
15.4 0.118 15.282,
n
1000
t S
1.91
x
15.4 1.96
15.4 0.118 15.518.
n
1000
Доверительный интервал: 15.282 a 15.518.
Полученный доверительный интервал означает, что
выбранная средняя x 15.4
оценивает среднюю
урожайность на площади в 10000 га с точность =0.118
и вероятностью 0.95.