Обернена пропорційність

1.

2. Задачі, які зводяться до поняття оберненої пропорційності.

Пішохід шлях S проходить зі швидкістю v
за t годин. Виразіть час пішохода
через шлях та швидкість.
60
1) Якщо S 60 , то t
v
1

3. Задачі, які зводяться до поняття оберненої пропорційності.

Пішохід шлях S проходить зі швидкістю v
за t годин. Виразіть час пішохода
через шлях та швидкість.
3
2) Якщо S 3 , то t
v
Як пов’язані між собою
швидкість та час?
1

4. Задачі, які зводяться до поняття оберненої пропорційності.

Площа прямокуника зі сторонами
x та y дорівнює S. Виразіть у через S та х.
24
1) Якшо S 24 , то у
х
2

5. Задачі, які зводяться до поняття оберненої пропорційності.

Площа прямокутника зі сторонами
x та y дорівнює S. Виразіть у через S та х.
6
2) Якщо S 6 , то у
х
Як пов’язані між собою х та у?
2

6. Задачі, які зводяться до поняття оберненої пропорційності.

За телеграму з х слів за ціною у грн. за
одне слово заплатили с грн.
Виразіть у через с и х.
90
1) Якщо с 90 , то у
х
3

7. Задачі, які зводяться до поняття оберненої пропорційності.

За телеграму з х слів за ціною у грн. за
одне слово заплатили с грн.
Виразіть у через с та х.
10
1) Якщо с 10 , то у
х
Яка залежність між х та у?
3

8. О з н а ч е н н я.

Оберненою пропорційністю
називається функція, яку
можна задати формулою вигляду
де х – незалежна змінна,
k – число, яке не дорівнює нулю.

9. Властивості функції

1
х 0
Область визначення функції є
множина всіх чисел, відмінних від нуля.
2
k 0 у 0
Областю значень функції є
множина всіх чисел, відмінних від нуля.

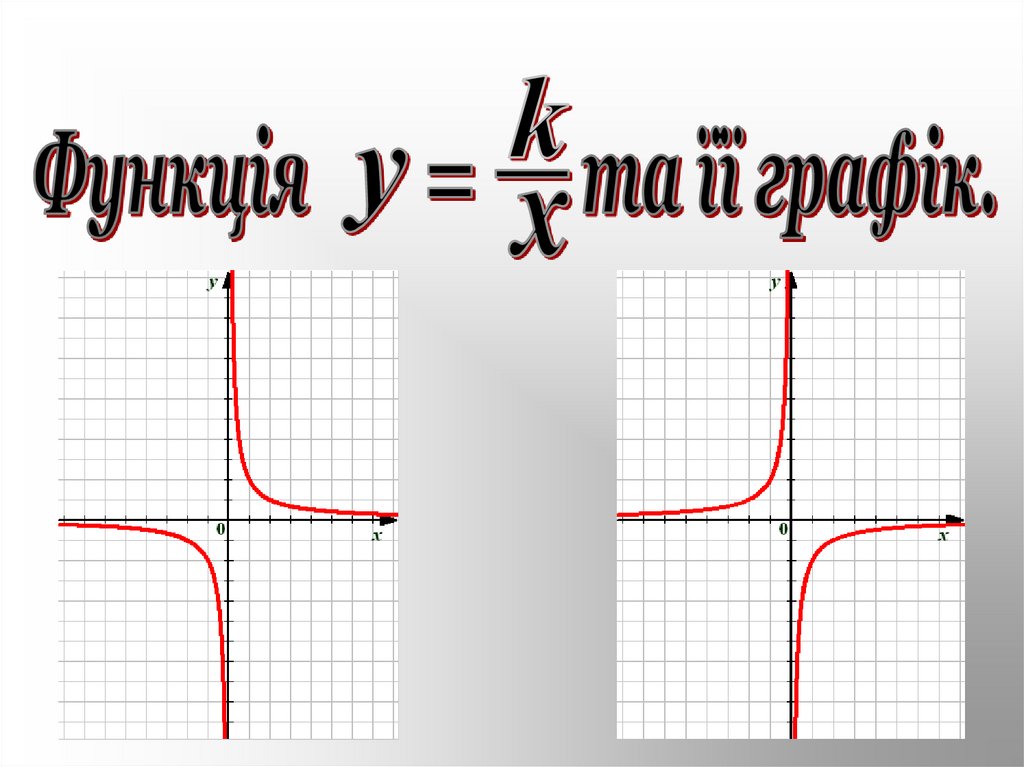
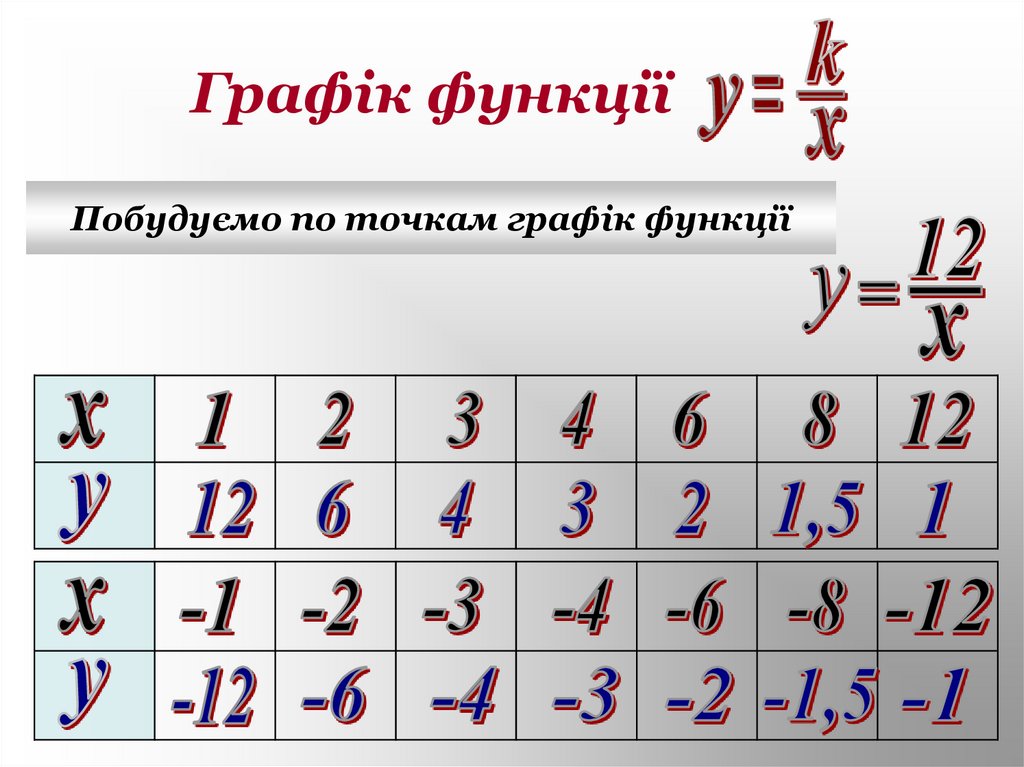
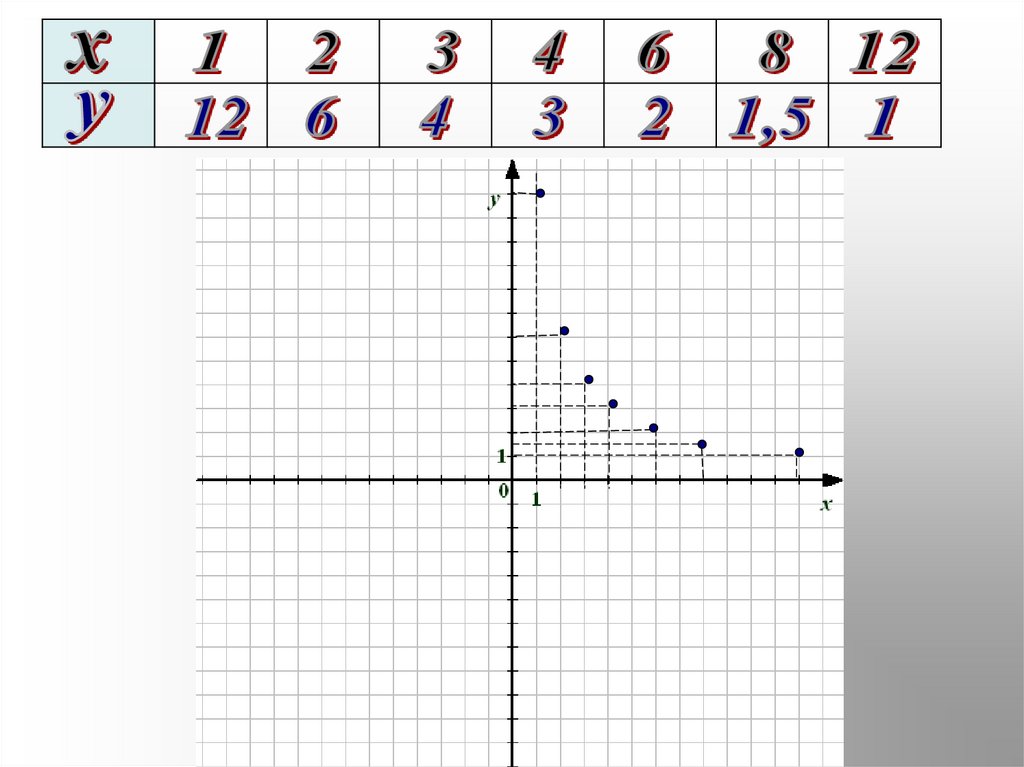
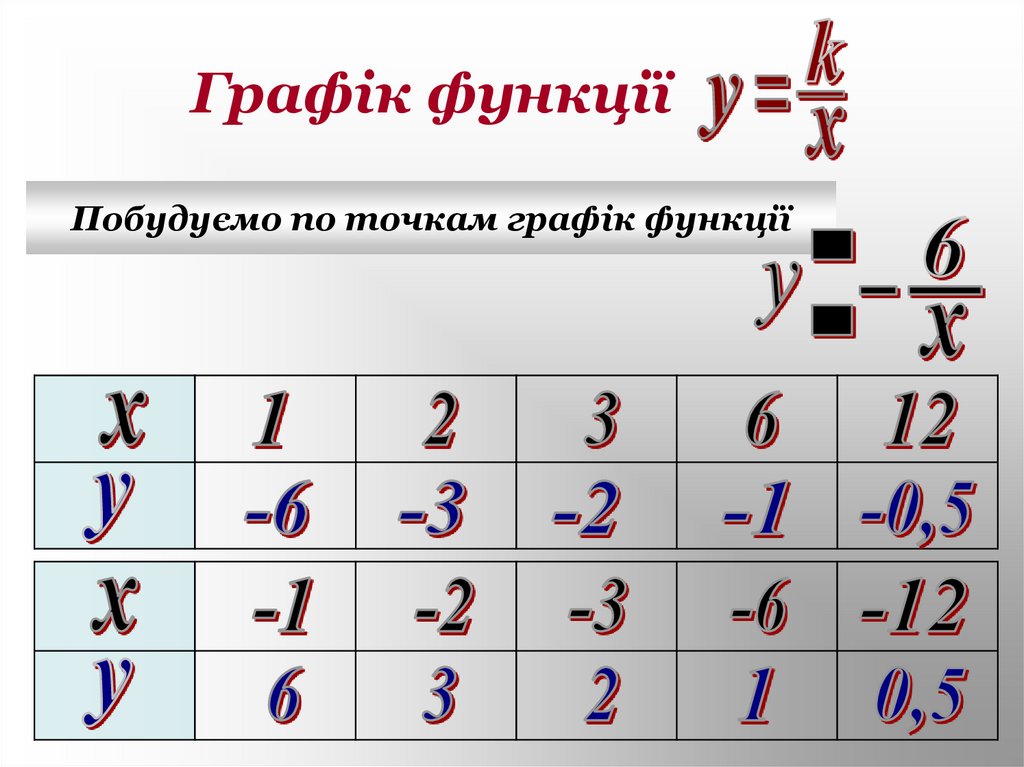
10. Графік функції

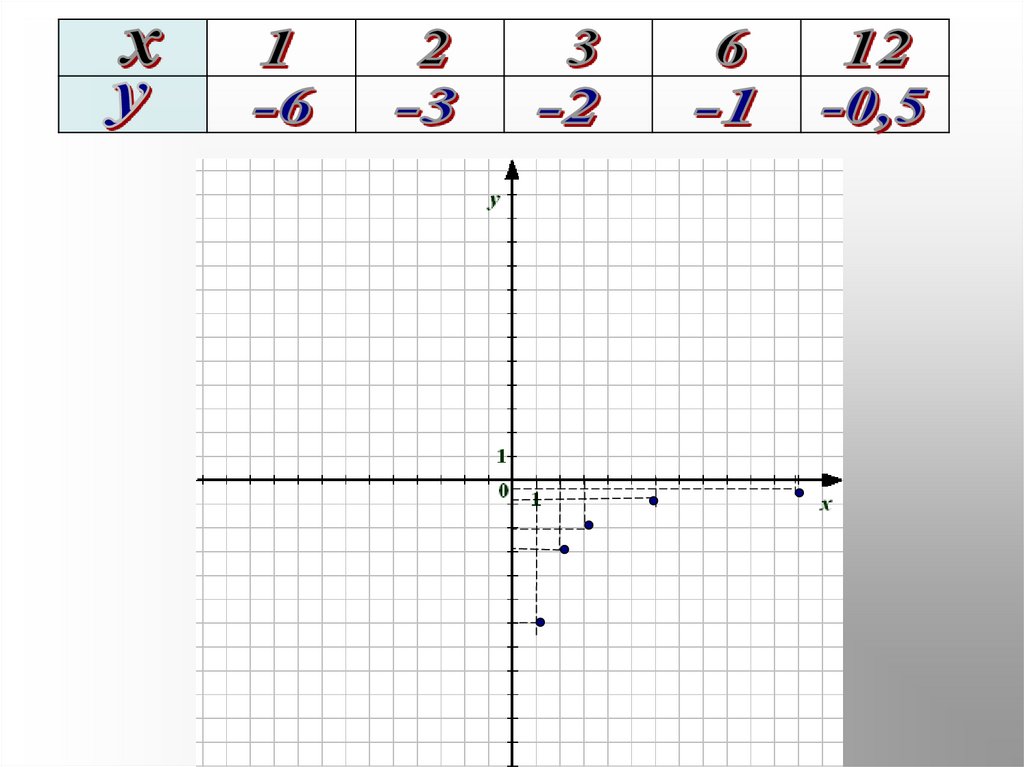
Побудуємо по точкам графік функції

11.

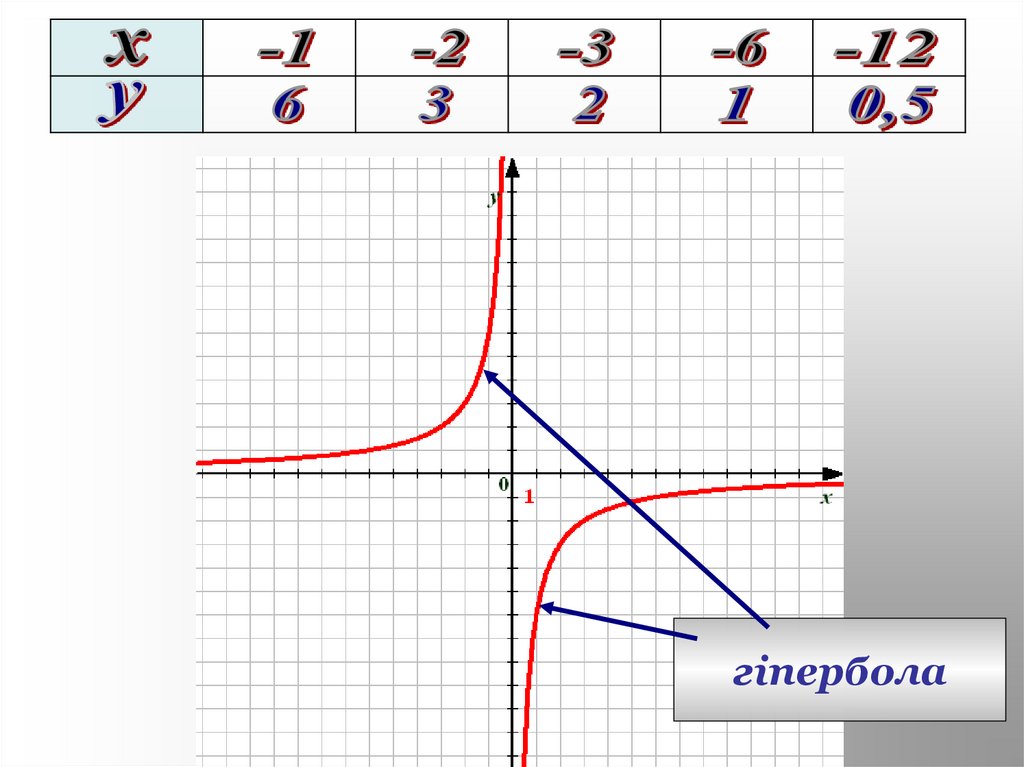
12.

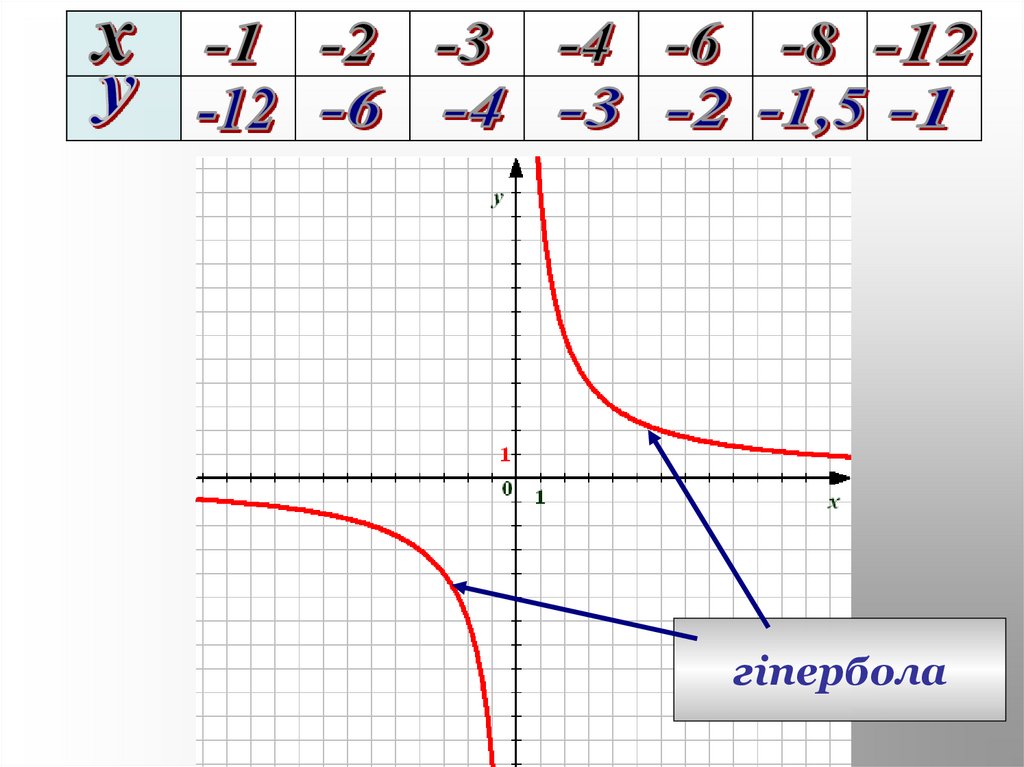
гіпербола

13. Графік функції

Побудуємо по точкам графік функції

14.

15.

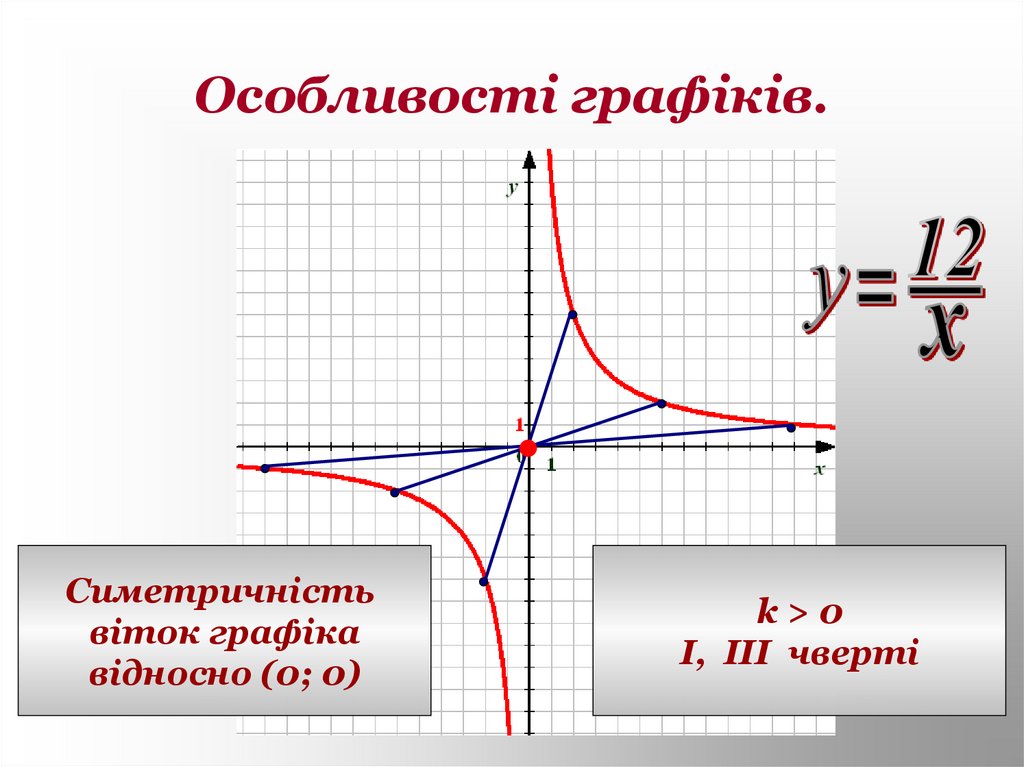
гіпербола

16. Особливості графіків.

Симетричність
віток графіка
відносно (0; 0)
k>0
I, III чверті

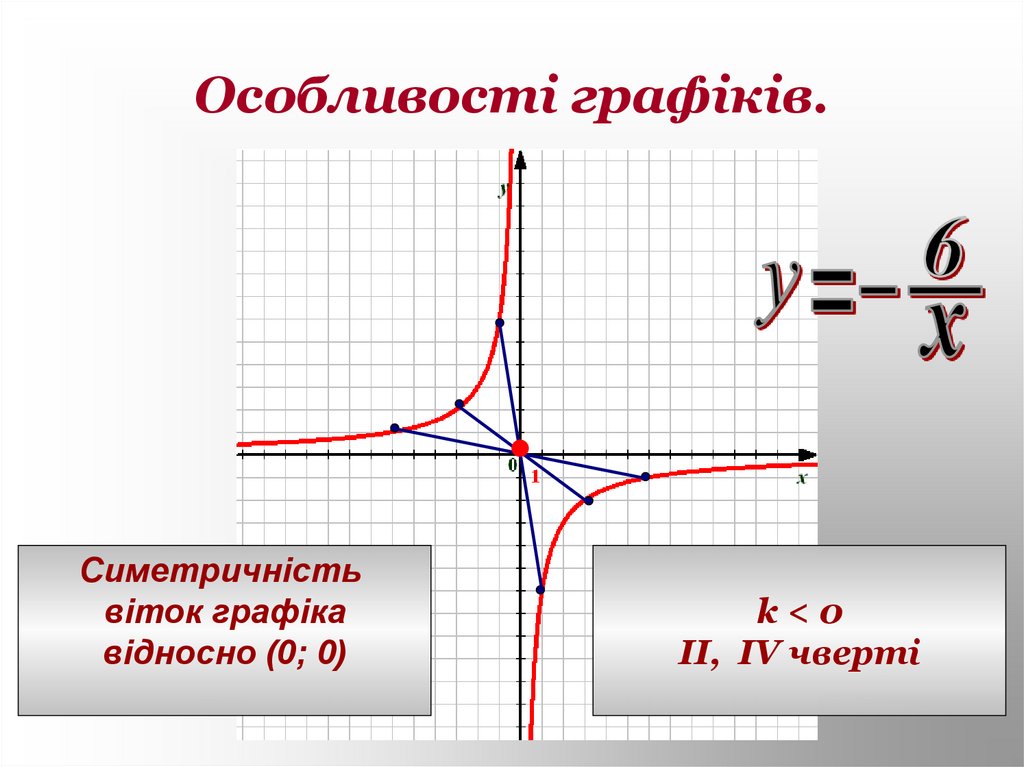
17. Особливості графіків.

Симетричність
віток графіка
відносно (0; 0)
k<0
II, IV чверті

18.

Завдання №1
Вказати, яку з функції
можна назвати
обрненою пропорційністю:
х
у
3
3
у
х
у 3х
у х 3
у х
3
1
у
3х

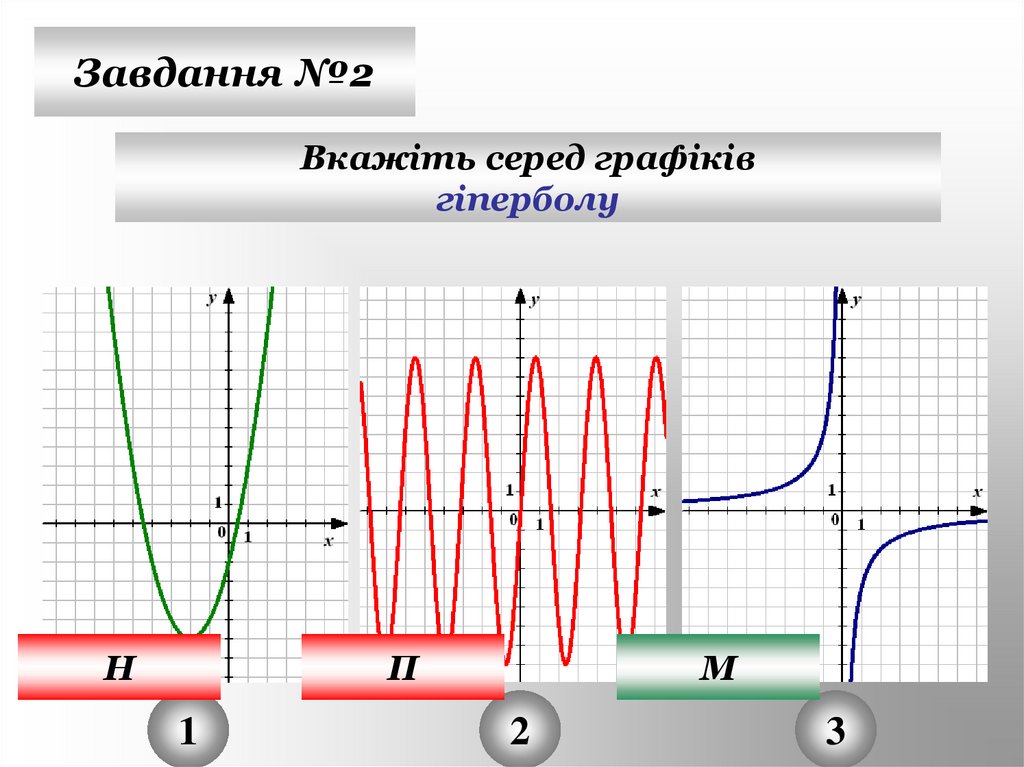
19.

Завдання №2
Вкажіть серед графіків
гіперболу
Н
П
1
М
2
3

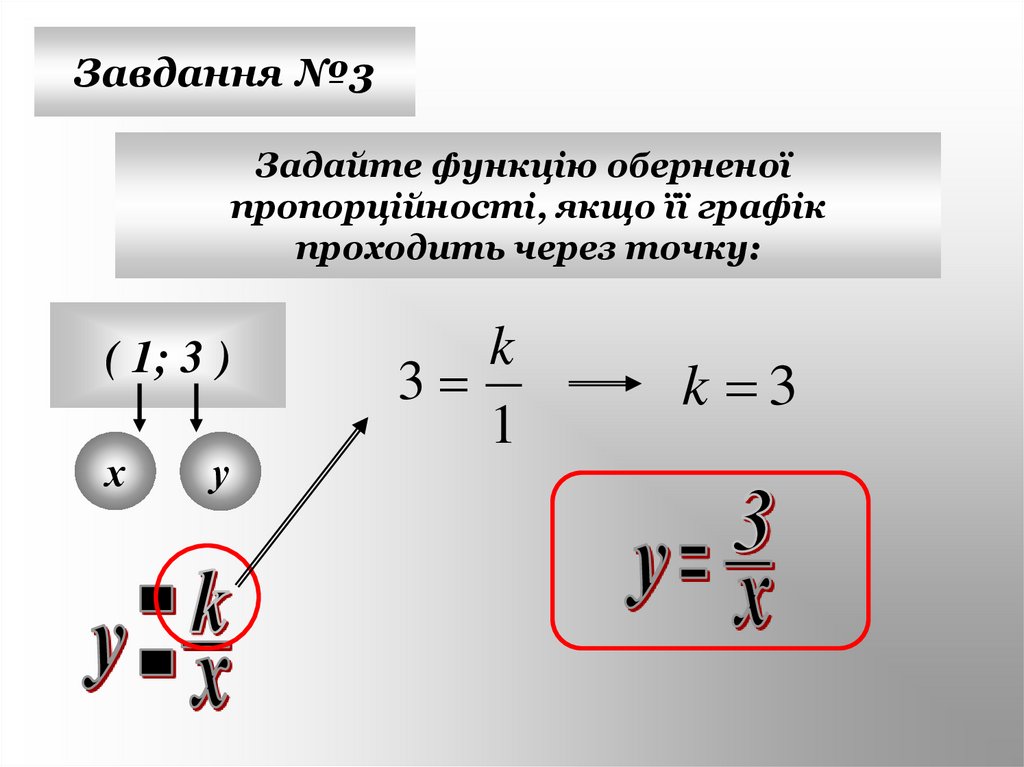
20.

Завдання №3
Задайте функцію оберненої
пропорційності, якщо її графік
проходить через точку:
( 1; 3 )
х
у
k
3
1
k 3

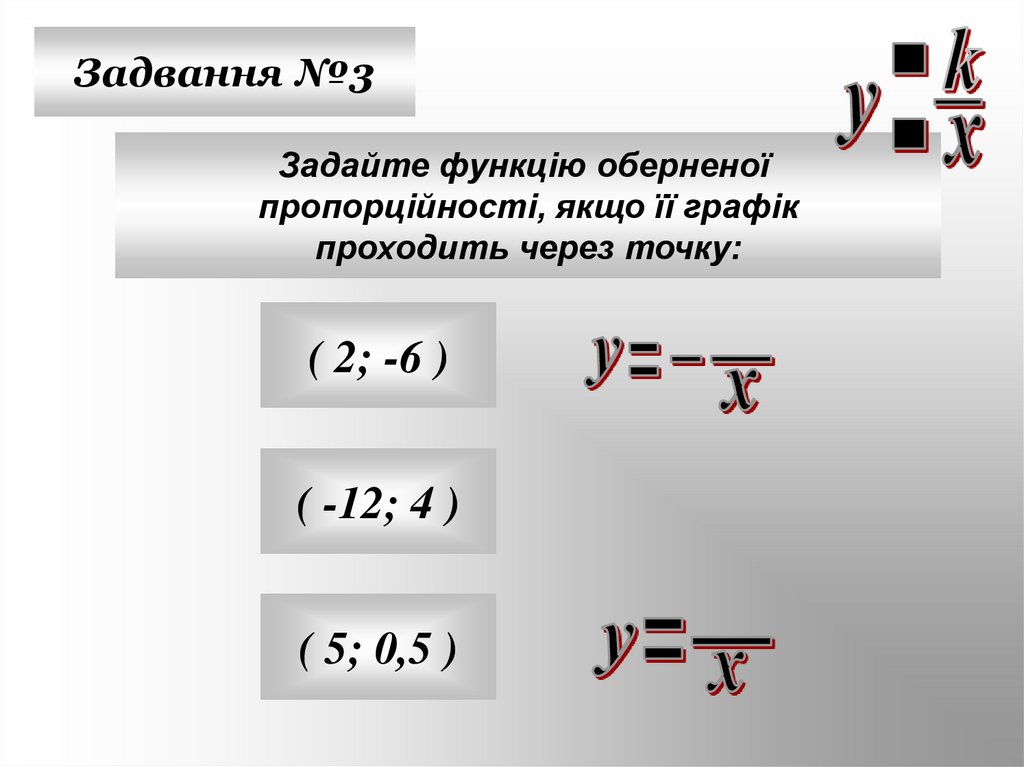
21.

Задвання №3
Задайте функцію оберненої
пропорційності, якщо її графік
проходить через точку:
( 2; -6 )
( -12; 4 )
( 5; 0,5 )

22.

Завдання №4
Побудуйте графік функції
Перевірка

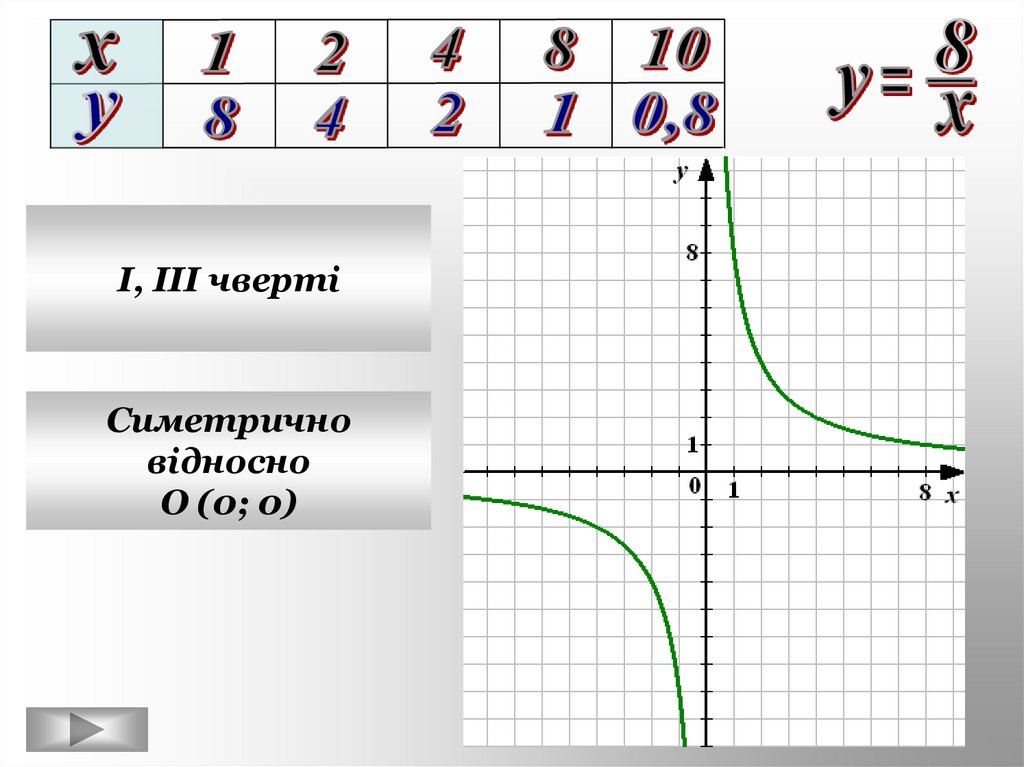
23.

I, III чверті
Симетрично
відносно
О (0; 0)

24.

Завдання №4
Побудуйте графік функції
Знайдіть за графіком:
1) Значення у, яке відповідає
значенню х, що дорівнює 2; 4; -1; -4; -5
Перевірка

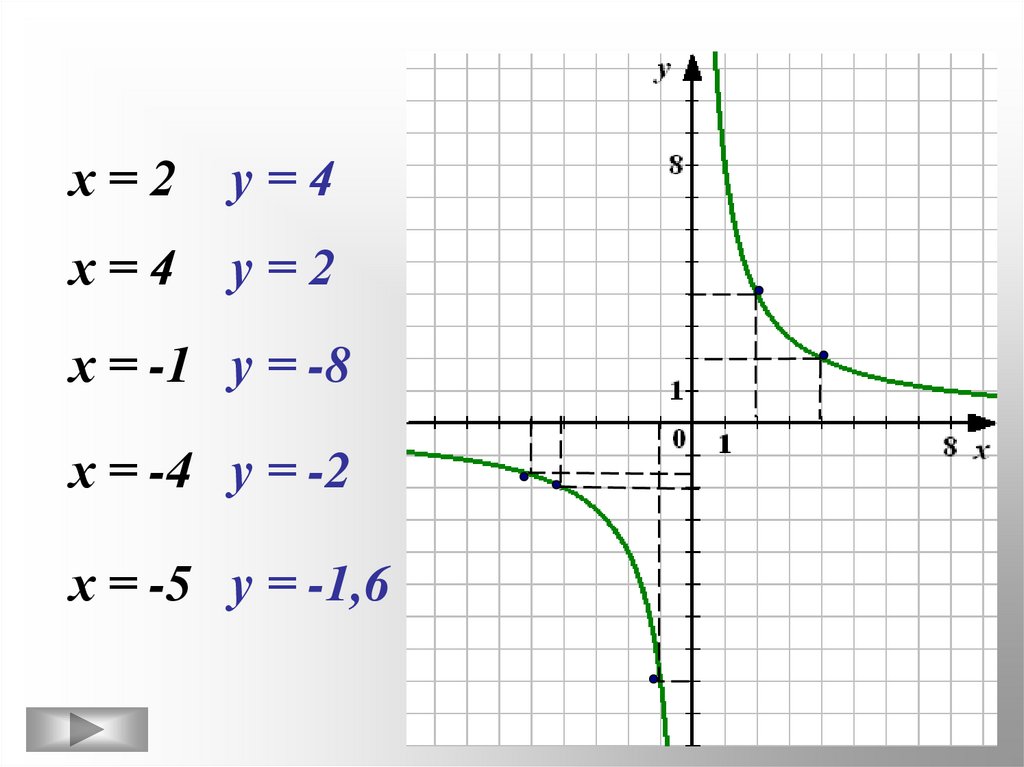
25.

х=2
у=4
х=4
у=2
х = -1 у = -8
х = -4 у = -2
х = -5 у = -1,6

26.

Завдання №4
Побудуйте графік функції
Знайдіть за графіком
значення у, яке відповідає
значенню х, що дорівнює 2; 4; -1; -4; -5
знайдіть за графіком:
значення х, якому відповідає
значення у, що дорівнює -4; -2; 8
Перевірка

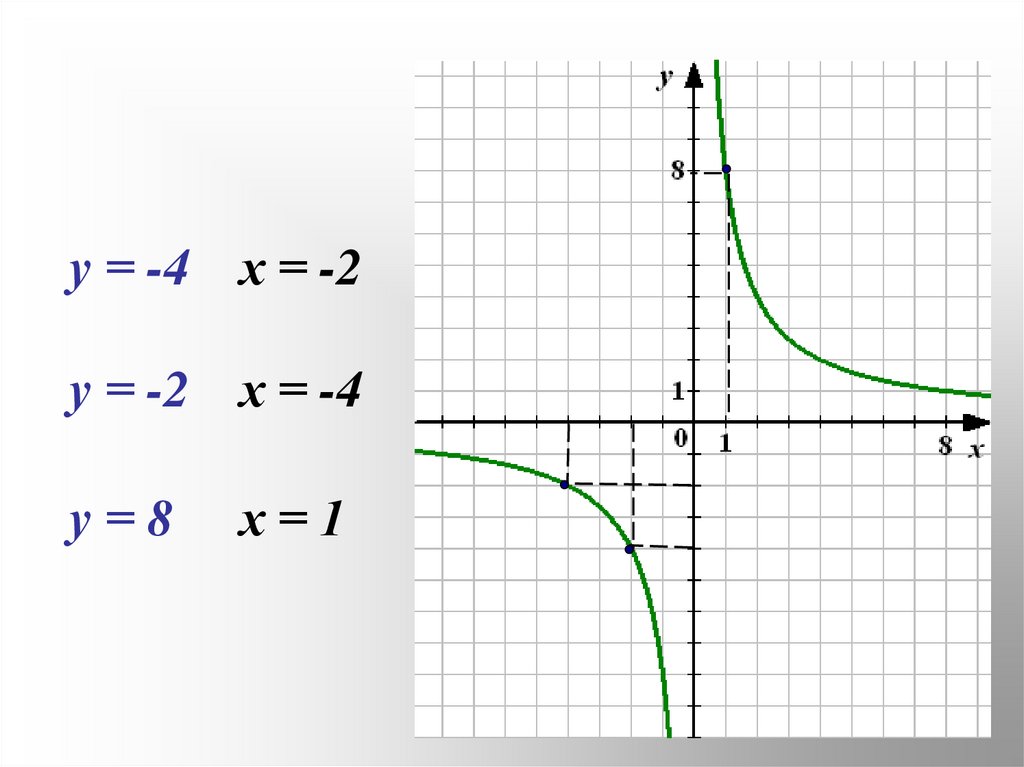
27.

у = -4 х = -2
у = -2 х = -4
у=8
х=1

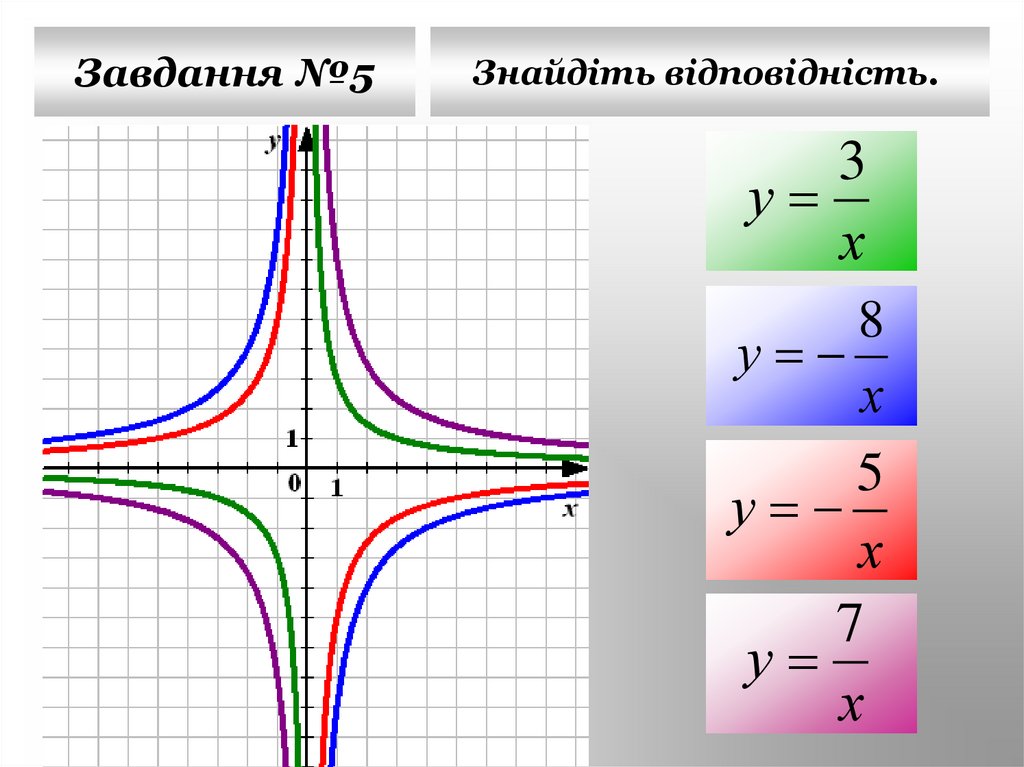
28.

Завдання №5
Знайдіть відповідність.
3
у
х
8
у
х
5
у
х
7
у
х