Похожие презентации:
Побудова графіків тригонометричних функцій
1.
Побудова графіківтригонометричних функцій
2. Практичне застосування тригонометричних функцій
Синусоїда – хвилеподібна плоска крива, яка єграфіком тригонометричної функції y = sinx в
прямокутній системі координат. Якщо рулон паперу
розрізати навскоси і розвернути його, то край
паперу виявиться розрізаним по синусоїді. Цікаво,
що проекція на площину гвинтової лінії свердла
також буде синусоїдою.
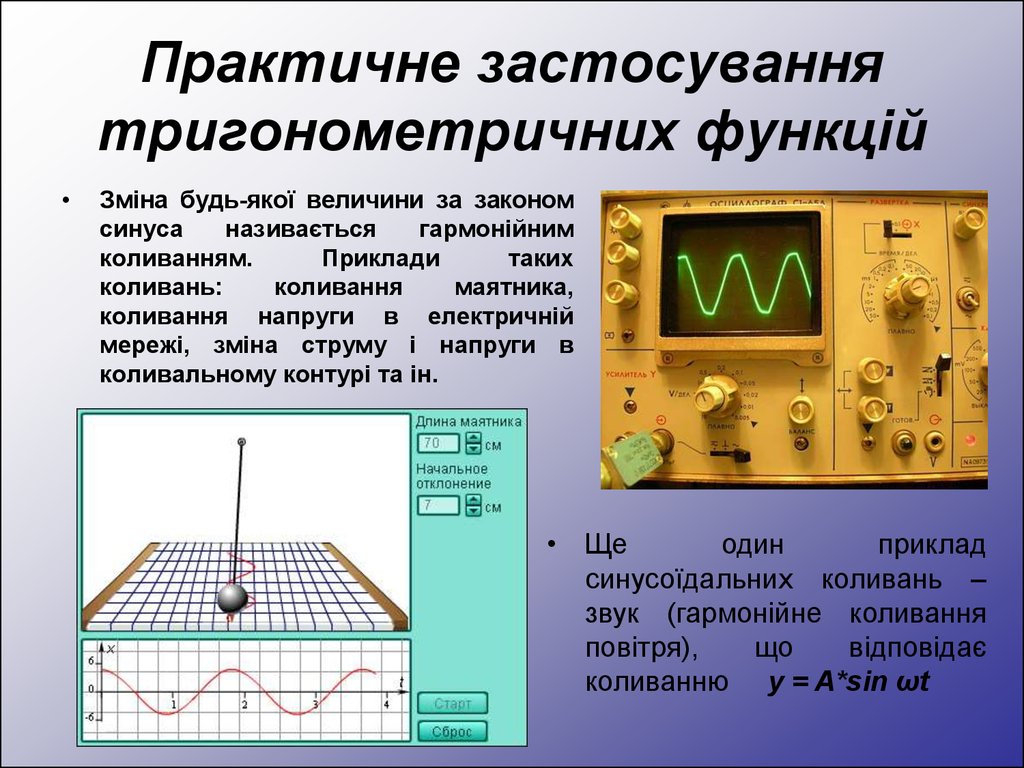
3. Практичне застосування тригонометричних функцій
Зміна будь-якої величини за законом
синуса
називається
гармонійним
коливанням.
Приклади
таких
коливань:
коливання
маятника,
коливання напруги в електричній
мережі, зміна струму і напруги в
коливальному контурі та ін.
• Ще
один
приклад
синусоїдальних коливань –
звук (гармонійне коливання
повітря),
що
відповідає
коливанню y = A*sin ωt
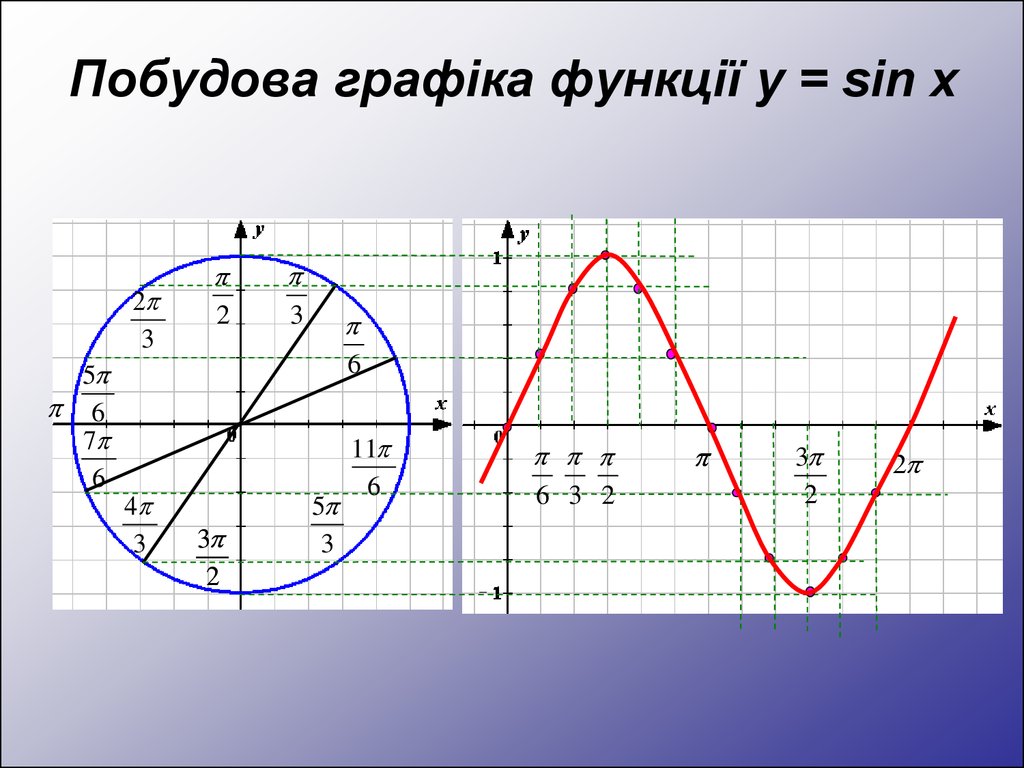
4. Побудова графіка функції y = sin x
23
5
6
7
6
2
3
6
4
3
3
2
5
3
11
6
6 3 2
3
2
2
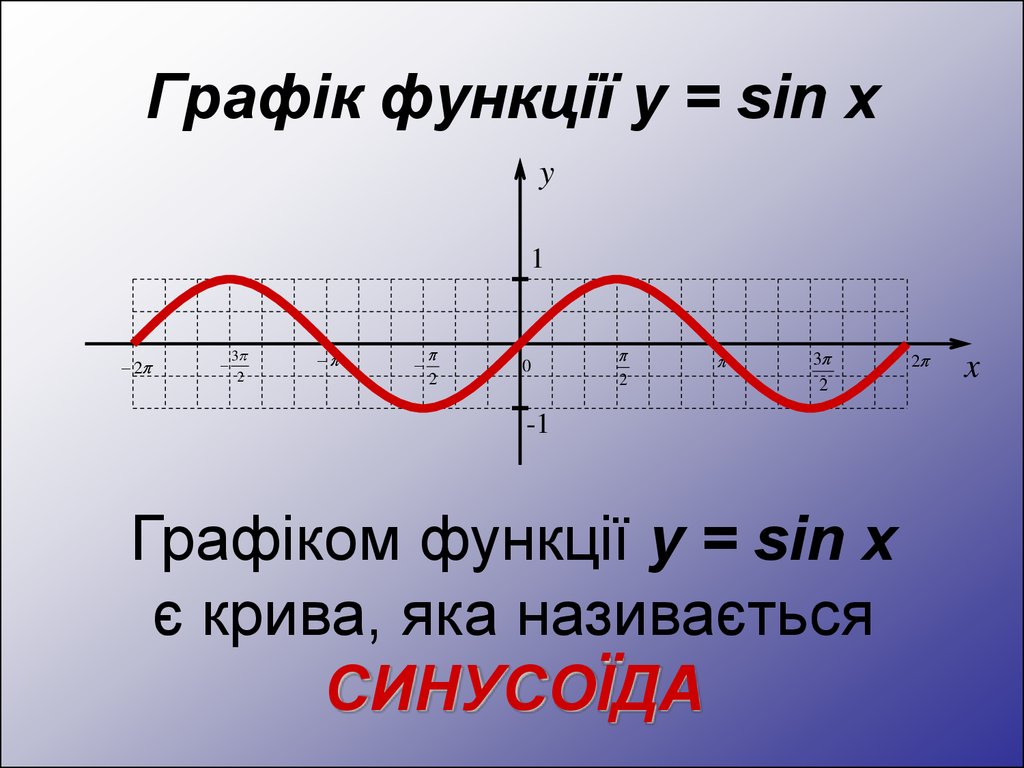
5. Графік функції y = sin x
y1
2
3
2
2
0
2
3
2
-1
Графіком функції y = sin x
є крива, яка називається
СИНУСОЇДА
2
x
6. Перетворення графіків функції
y sin x7. Перетворення графіків функції y = sin x
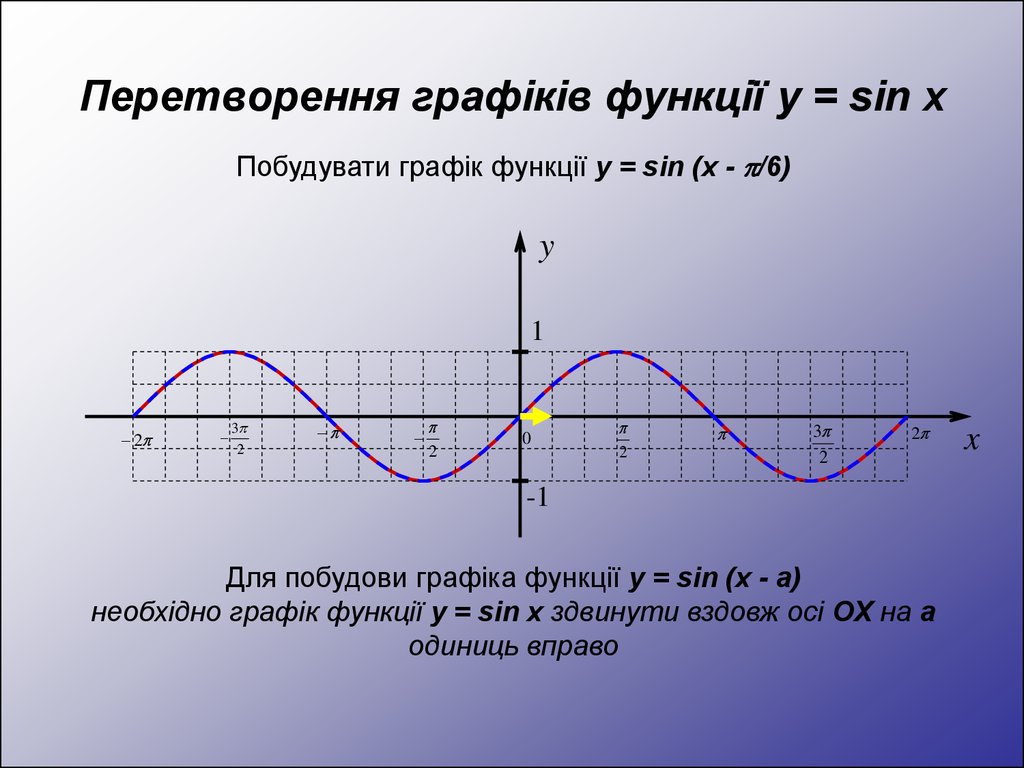
Побудувати графік функції y = sin (x - /6)y
1
2
3
2
2
0
2
3
2
2
-1
Для побудови графіка функції y = sin (x - а)
необхідно графік функції y = sin x здвинути вздовж осі OX на а
одиниць вправо
x
8. Перетворення графіків функції y = sin x
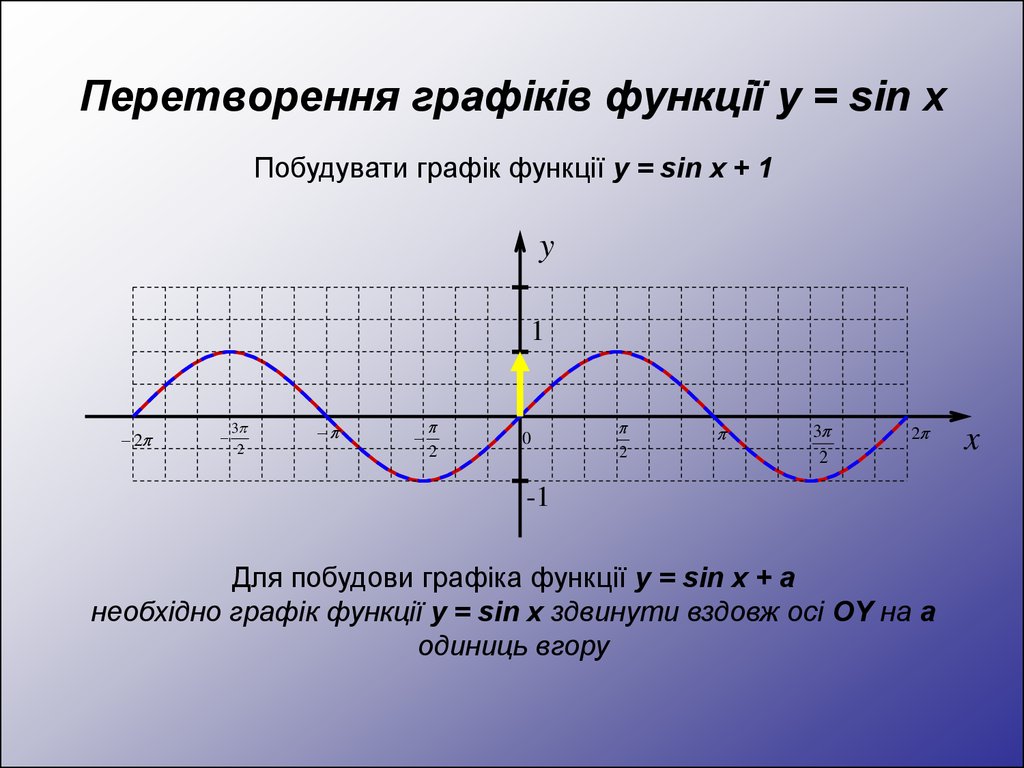
Побудувати графік функції y = sin x + 1y
1
2
3
2
2
0
2
3
2
2
-1
Для побудови графіка функції y = sin x + а
необхідно графік функції y = sin x здвинути вздовж осі OY на а
одиниць вгору
x
9. Перетворення графіків функції y = sin x
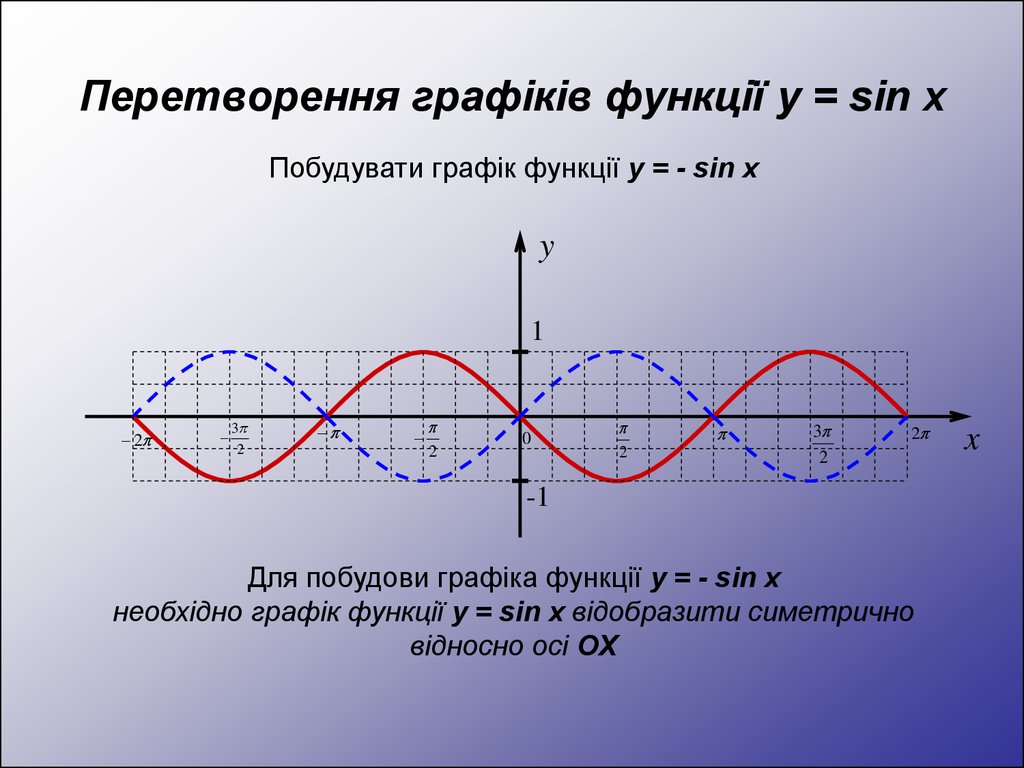
Побудувати графік функції y = - sin xy
1
2
3
2
2
0
2
3
2
2
-1
Для побудови графіка функції y = - sin x
необхідно графік функції y = sin x відобразити симетрично
відносно осі OX
x
10. Перетворення графіків функції y = sin x
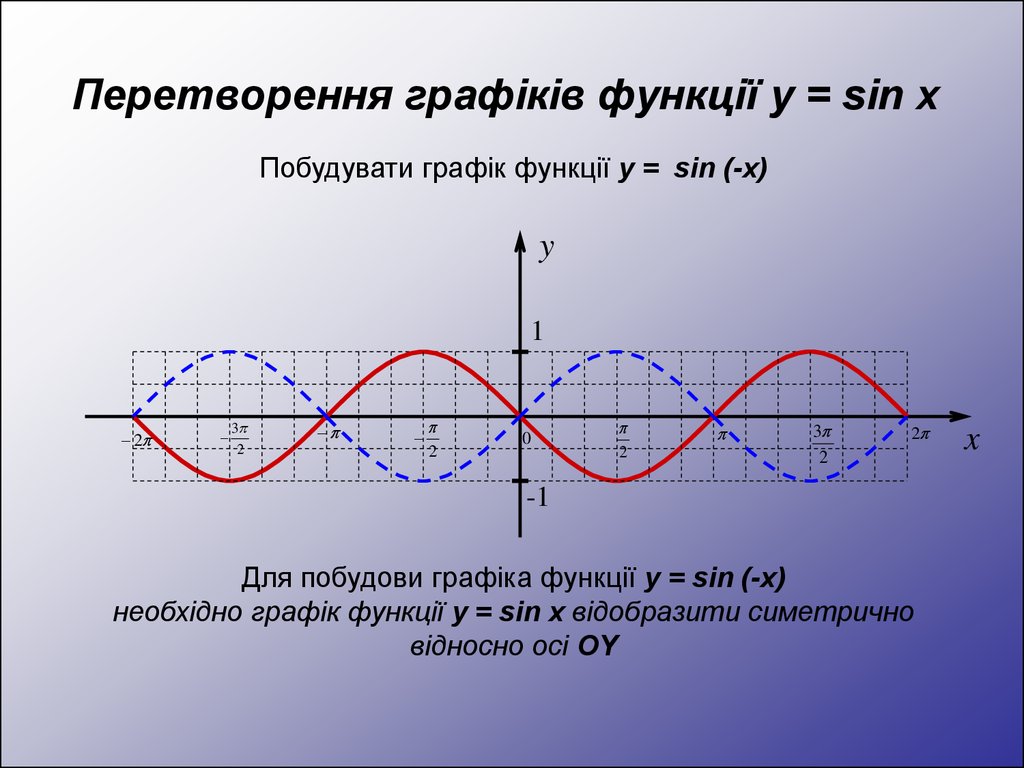
Побудувати графік функції y = sin (-x)y
1
2
3
2
2
0
2
3
2
2
-1
Для побудови графіка функції y = sin (-x)
необхідно графік функції y = sin x відобразити симетрично
відносно осі OY
x
11. Перетворення графіків функції y = sin x
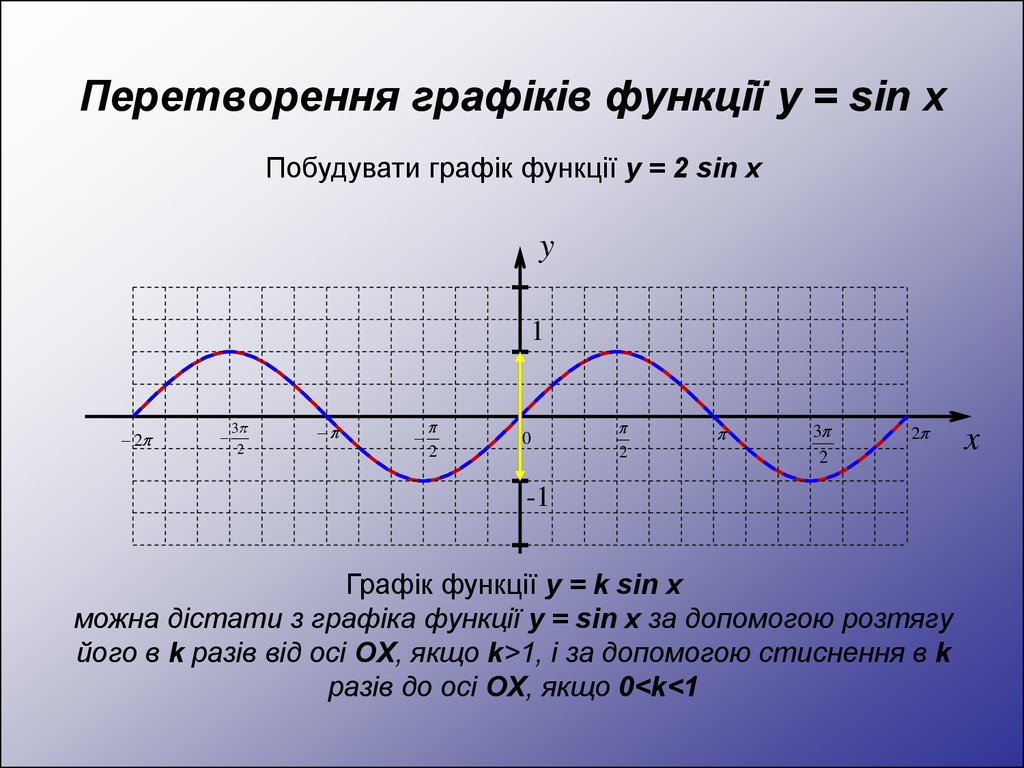
Побудувати графік функції y = 2 sin xy
1
2
3
2
2
0
2
3
2
2
-1
Графік функції y = k sin x
можна дістати з графіка функції y = sin x за допомогою розтягу
його в k разів від осі OX, якщо k>1, і за допомогою стиснення в k
разів до осі OX, якщо 0<k<1
x
12. Перетворення графіків функції y = sin x
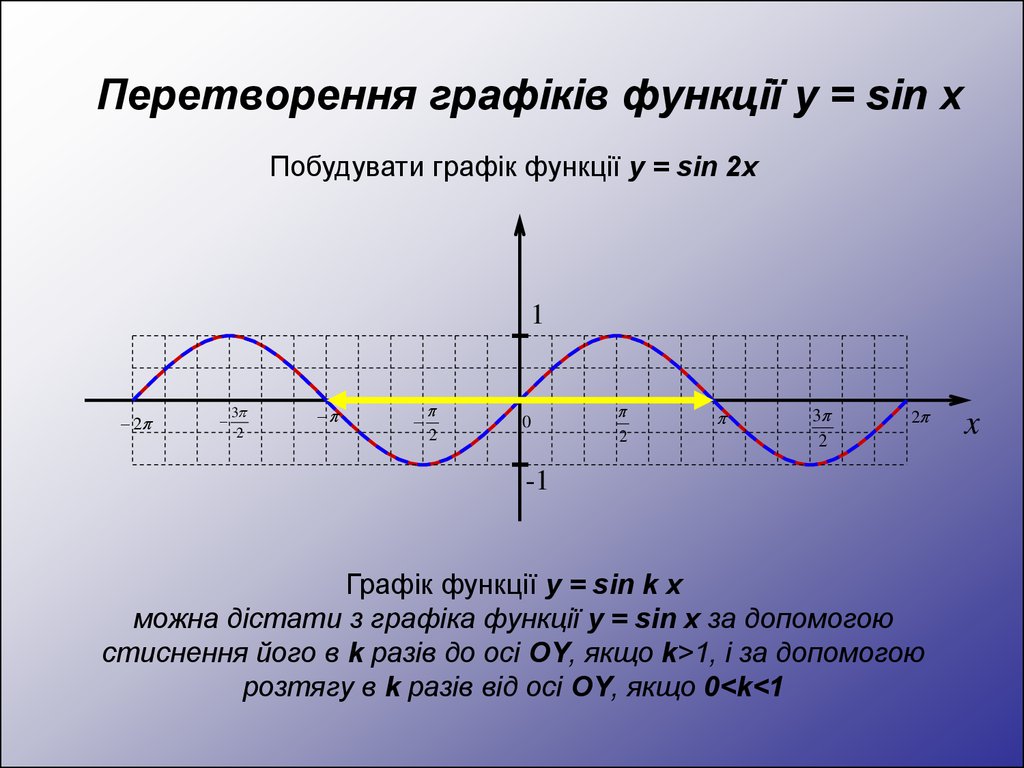
Побудувати графік функції y = sin 2x1
2
3
2
2
0
2
3
2
2
-1
Графік функції y = sin k x
можна дістати з графіка функції y = sin x за допомогою
стиснення його в k разів до осі OY, якщо k>1, і за допомогою
розтягу в k разів від осі OY, якщо 0<k<1
x
13. Перетворення графіків функції y = sin x
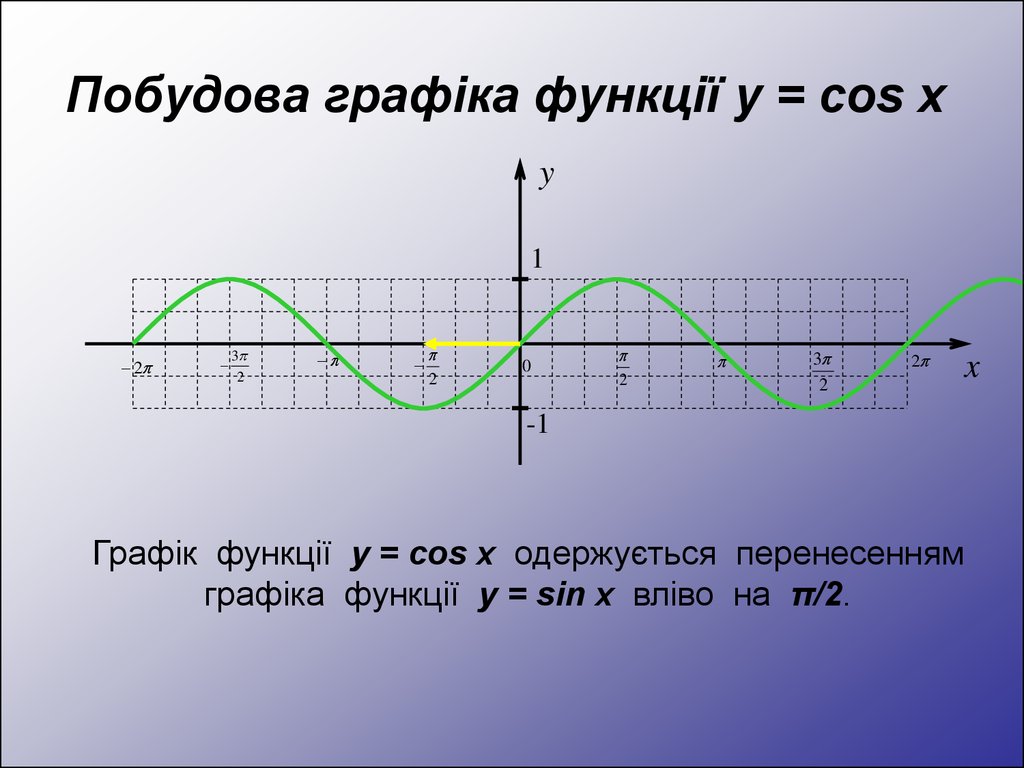
Побудова графіка функції y = cos xy
1
2
3
2
2
0
2
3
2
2
x
-1
Графік функції у = cos x одержується перенесенням
графіка функції у = sin x вліво на π/2.
14. Перетворення графіків функції y = sin x
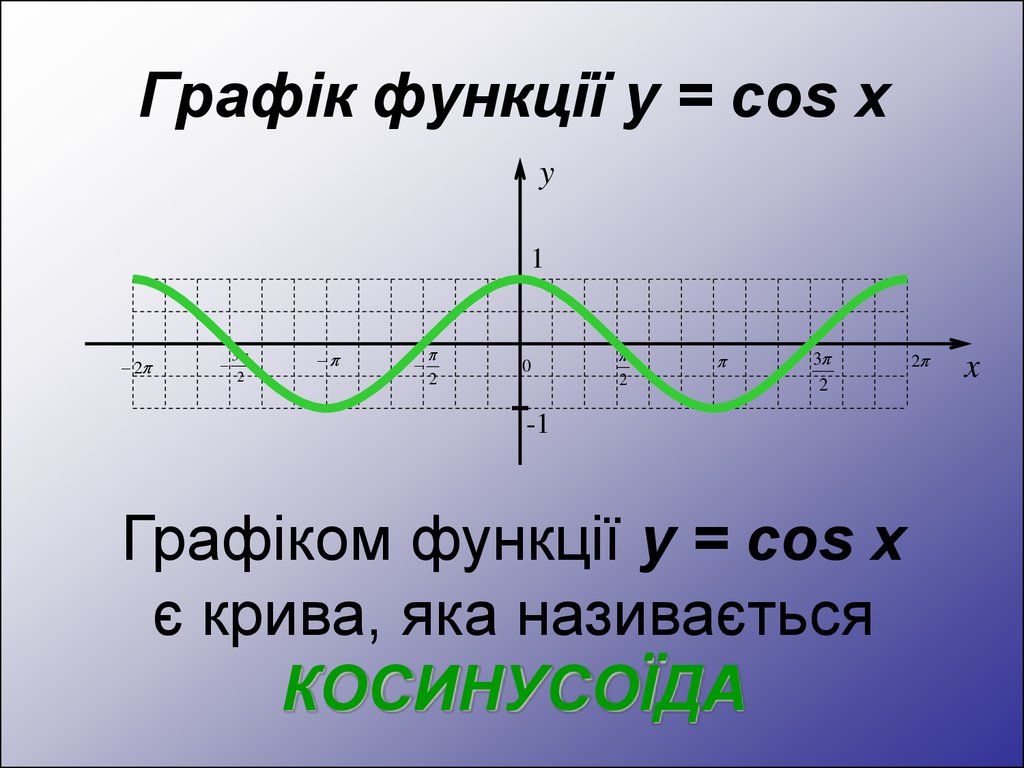
Графік функції y = cos xy
1
2
3
2
2
0
2
3
2
-1
Графіком функції y = cos x
є крива, яка називається
КОСИНУСОЇДА
2
x
15. Перетворення графіків функції y = sin x
Перетворення графіків функції y = cos xПеретворення графіків функції y = cos x
відбувається аналогічно перетворенню
графіків функції y = sin x
16. Перетворення графіків функції y = sin x
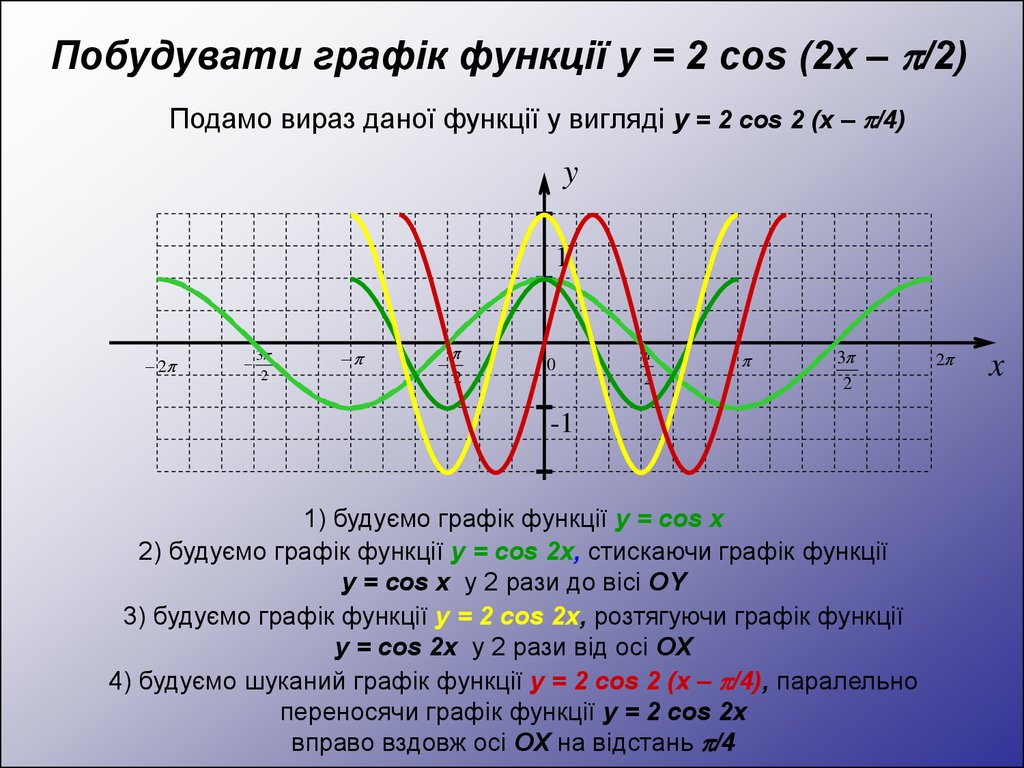
Побудувати графік функції y = 2 cos (2x – /2)Подамо вираз даної функції у вигляді y = 2 cos 2 (x – /4)
y
1
2
3
2
2
0
2
3
2
-1
1) будуємо графік функції y = cos x
2) будуємо графік функції y = cos 2x, стискаючи графік функції
y = cos x у 2 рази до вісі OY
3) будуємо графік функції y = 2 cos 2x, розтягуючи графік функції
y = cos 2x у 2 рази від осі OX
4) будуємо шуканий графік функції y = 2 cos 2 (x – /4), паралельно
переносячи графік функції y = 2 cos 2x
вправо вздовж осі OX на відстань /4
2
x
17. Перетворення графіків функції y = sin x
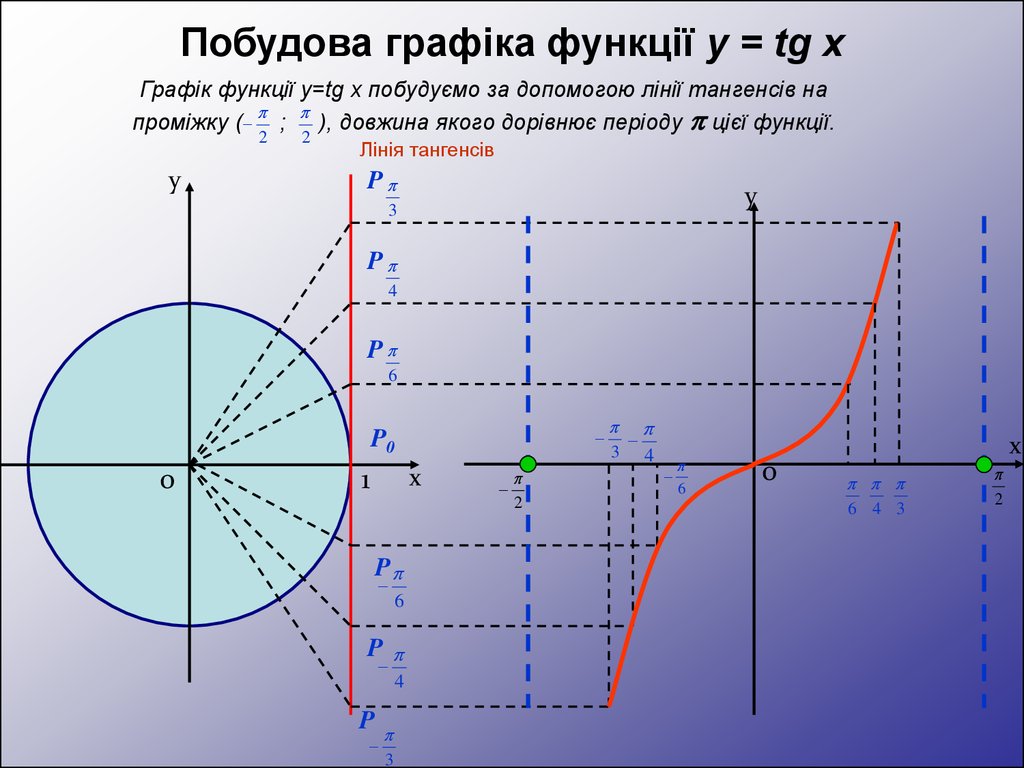
Побудова графіка функції y = tg xГрафік функції y=tg x побудуємо за допомогою лінії тангенсів на
проміжку ( ; ), довжина якого дорівнює періоду цієї функції.
2
у
2
Лінія тангенсів
P
у
3
P
4
P
6
P0
0
х
1
P
P
P
6
3
4
2
3
4
6
0
х
6 4 3
2
18. Перетворення графіків функції y = sin x
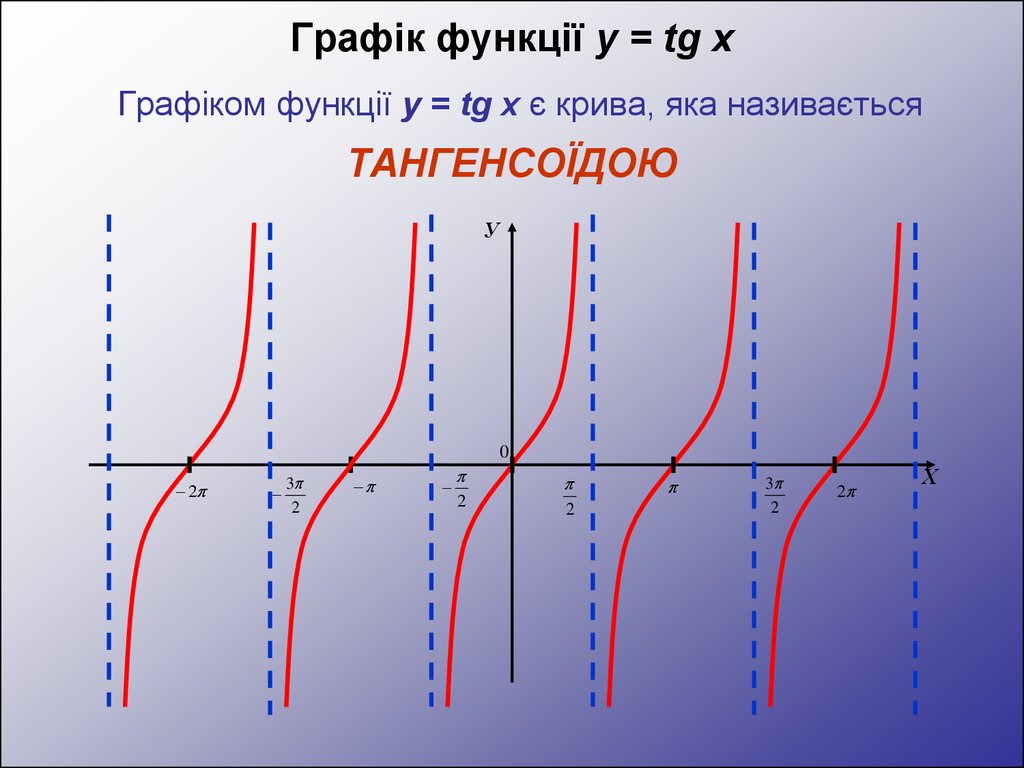
Графік функції y = tg xГрафіком функції y = tg x є крива, яка називається
ТАНГЕНСОЇДОЮ
У
0
2
3
2
2
2
3
2
2
Х
19. Означення тригонометричної функції
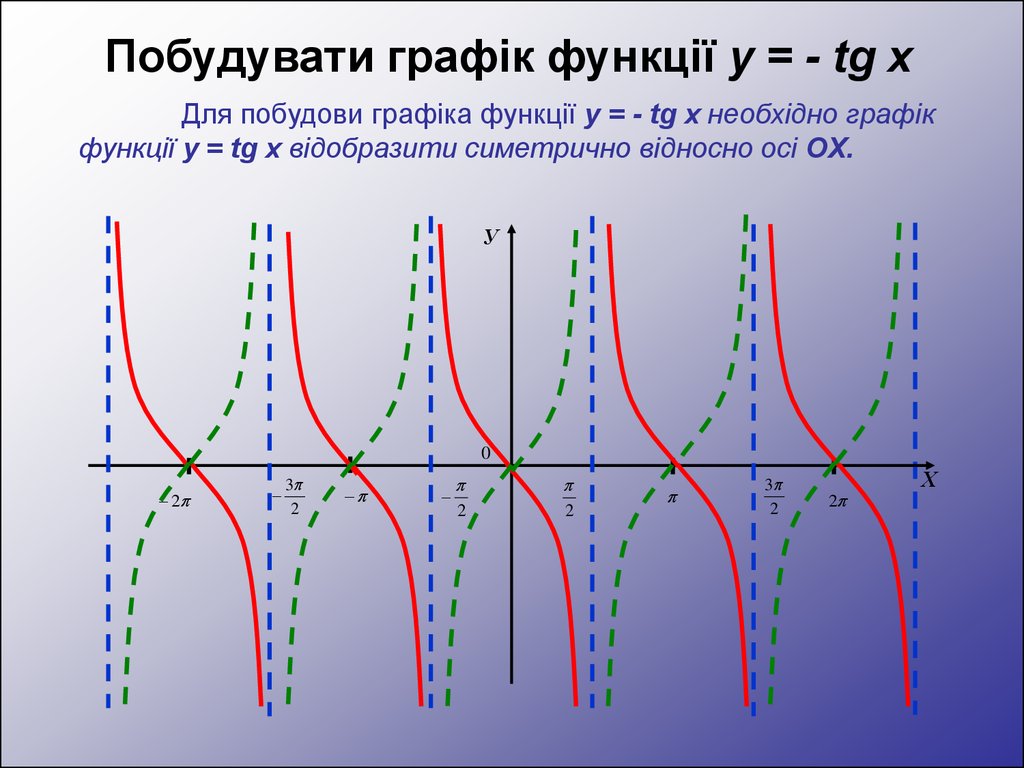
Побудувати графік функції y = - tg xДля побудови графіка функції y = - tg x необхідно графік
функції y = tg x відобразити симетрично відносно осі OX.
У
0
2
3
2
2
2
3
2
2
Х
20. Побудова графіка функції y = cos x
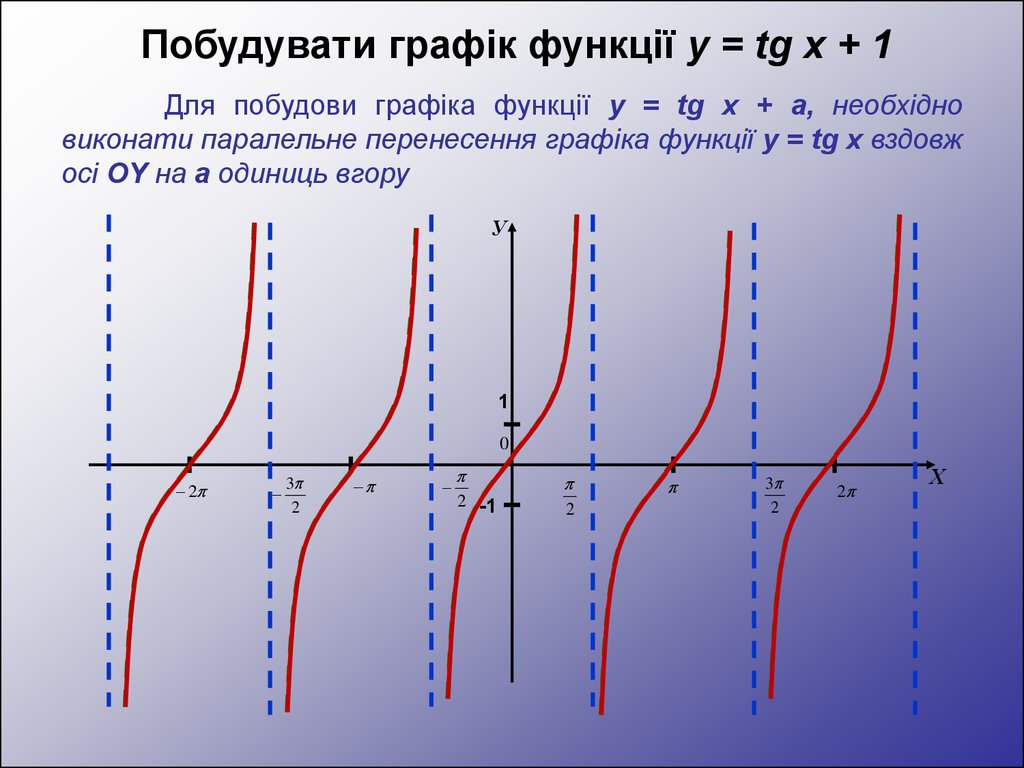
Побудувати графік функції y = tg x + 1Для побудови графіка функції y = tg x + а, необхідно
виконати паралельне перенесення графіка функції y = tg x вздовж
осі OY на а одиниць вгору
У
1
0
2
3
2
2 -1
2
3
2
2
Х
21. Графік функції y = cos x
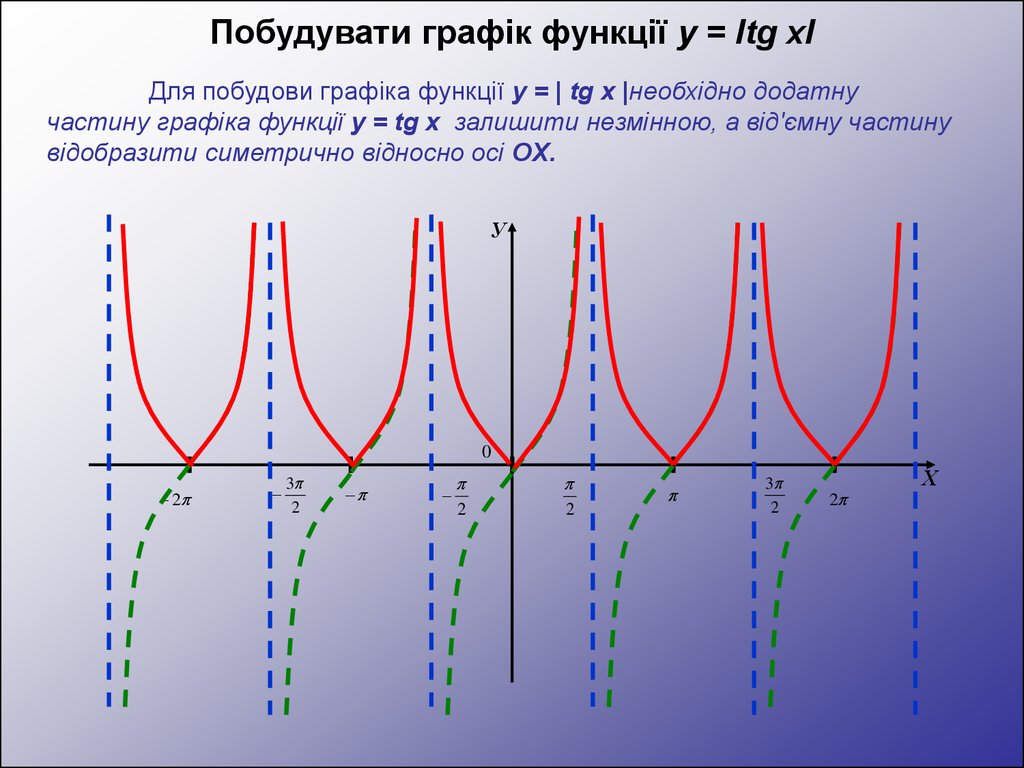
Побудувати графік функції y = Іtg xІДля побудови графіка функції y = | tg x |необхідно додатну
частину графіка функції y = tg x залишити незмінною, а від'ємну частину
відобразити симетрично відносно осі OX.
У
0
2
3
2
2
2
3
2
2
Х
22. Перетворення графіків функції y = cos x
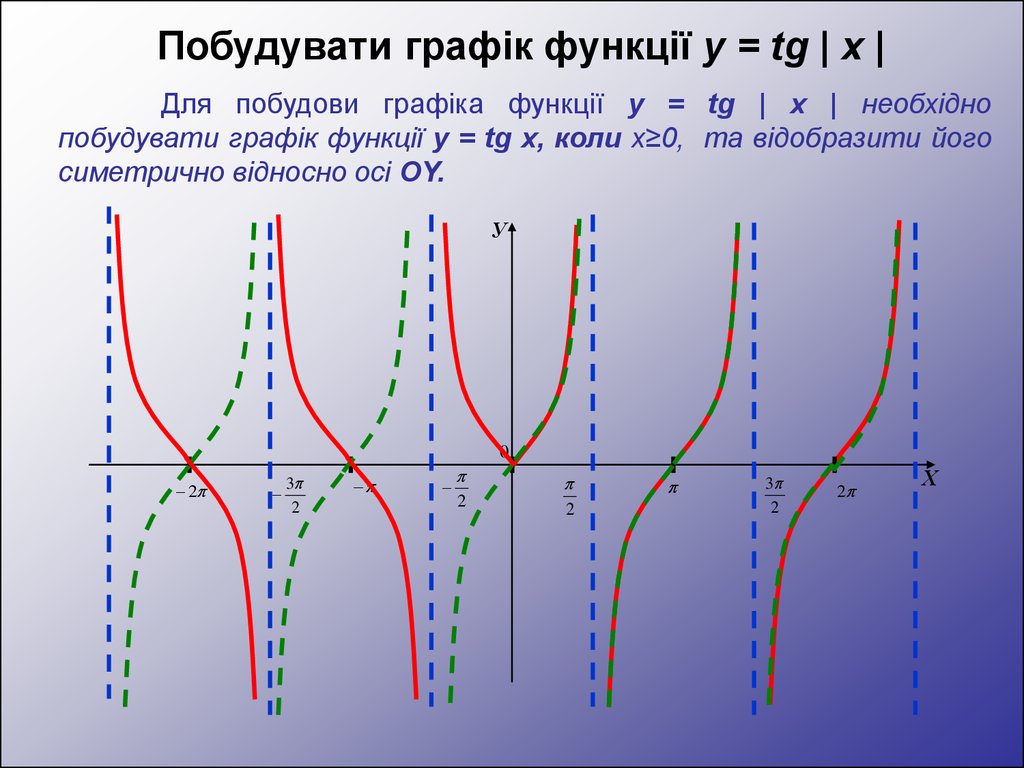
Побудувати графік функції y = tg | x |Для побудови графіка функції y = tg | x | необхідно
побудувати графік функції y = tg x, коли x≥0, та відобразити його
симетрично відносно осі OY.
У
0
2
3
2
2
2
3
2
2
Х
23.
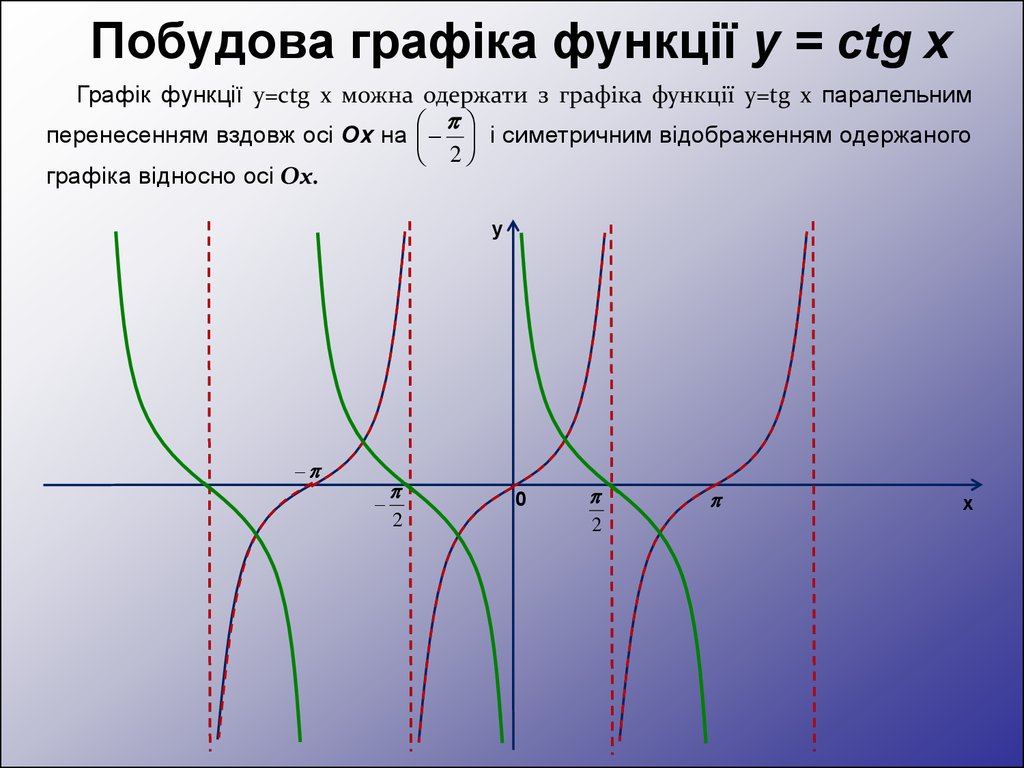
Побудова графіка функції y = ctg xГрафік функції y=ctg x можна одержати з графіка функції y=tg x паралельним
перенесенням вздовж осі Ox на і симетричним відображенням одержаного
2
графіка відносно осі Ox.
y
2
0
2
x
24.
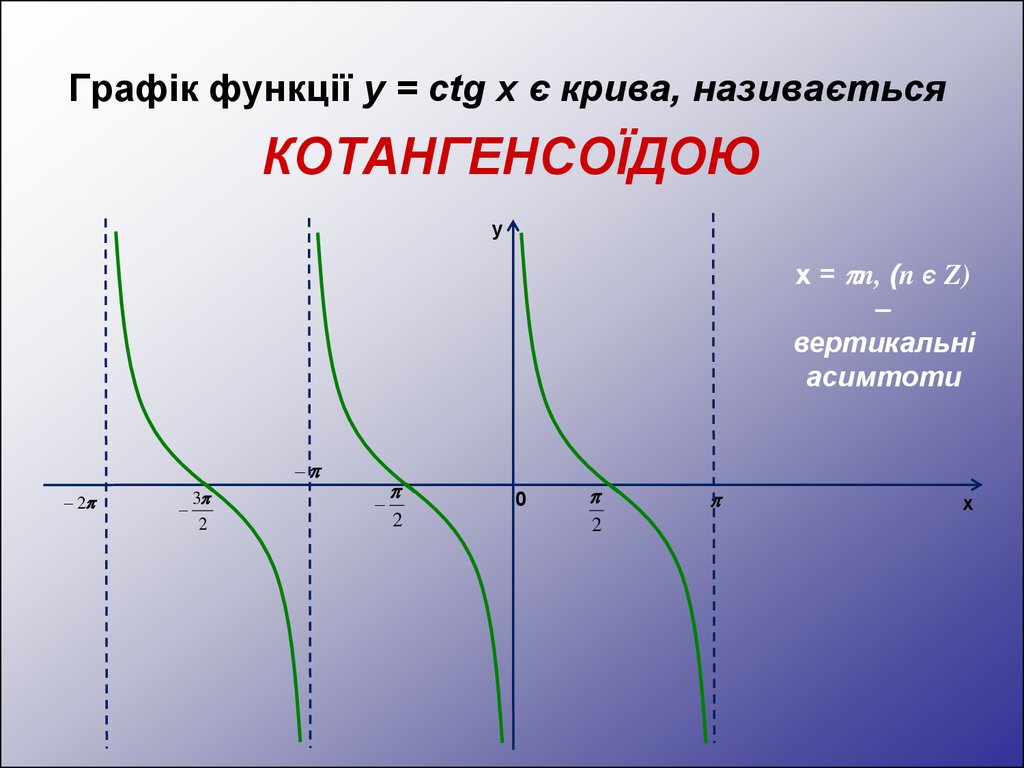
Графік функції y = сtg x є крива, називаєтьсяКОТАНГЕНСОЇДОЮ
y
х = n, (n Є Z)
–
вертикальні
асимтоти
2
3
2
2
0
2
x
25. Графік функції y = tg x Графіком функції y = tg x є крива, яка називається
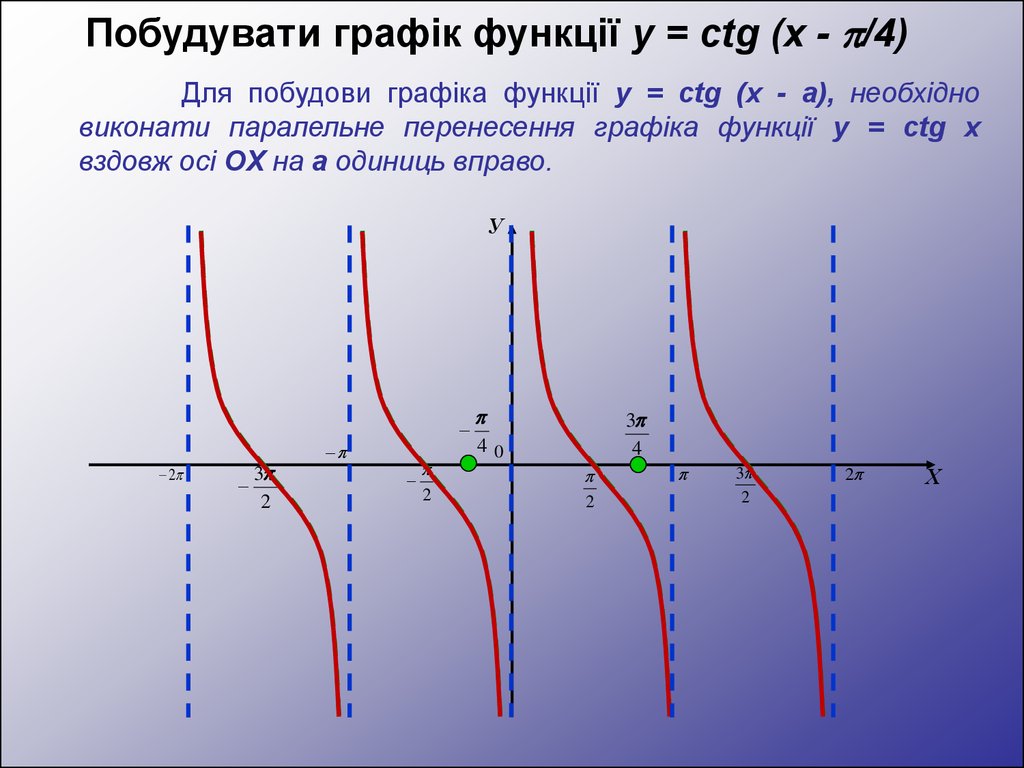
Побудувати графік функції y = сtg (x - /4)Для побудови графіка функції y = сtg (x - а), необхідно
виконати паралельне перенесення графіка функції y = сtg x
вздовж осі OX на а одиниць вправо.
У
2
3
2
2
3
4
40
2
3
2
2
Х
26.
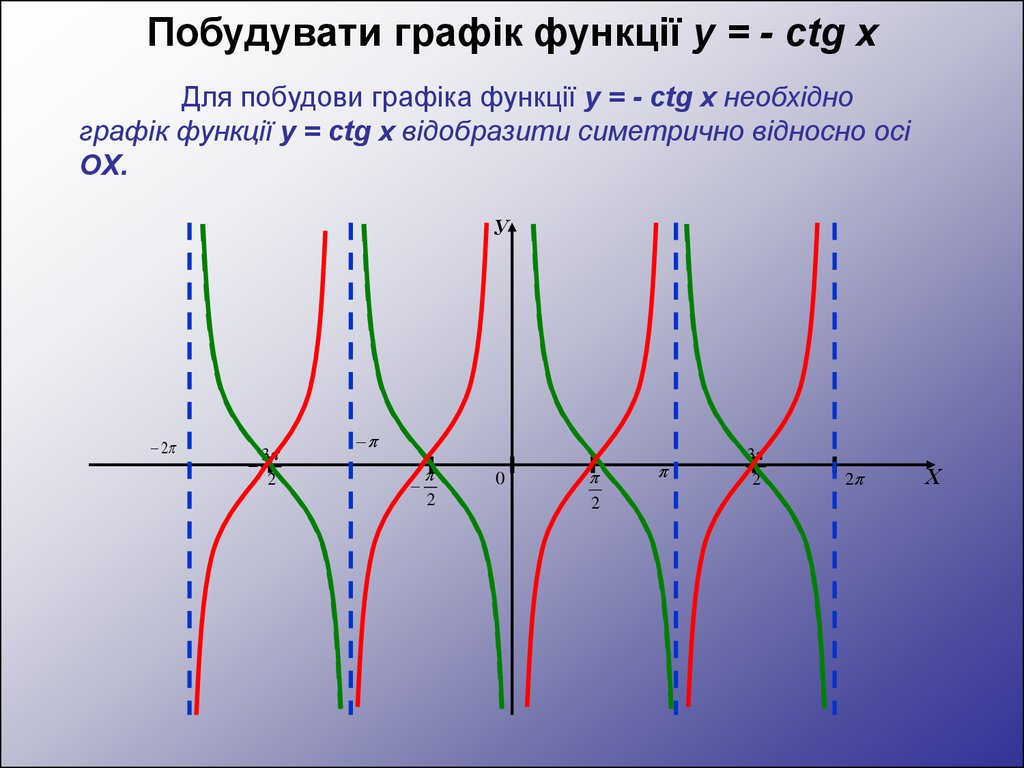
Побудувати графік функції y = - сtg xДля побудови графіка функції y = - сtg x необхідно
графік функції y = сtg x відобразити симетрично відносно осі
OX.
У
2
3
2
2
0
2
3
2
2
Х
27.
Рефлексія:1) Вам було на уроці:
• ЛЕГКО;
• ВАЖКО;
• ЗВИЧНО.
2) Що вам було не зрозуміло сьогодні на
занятті?


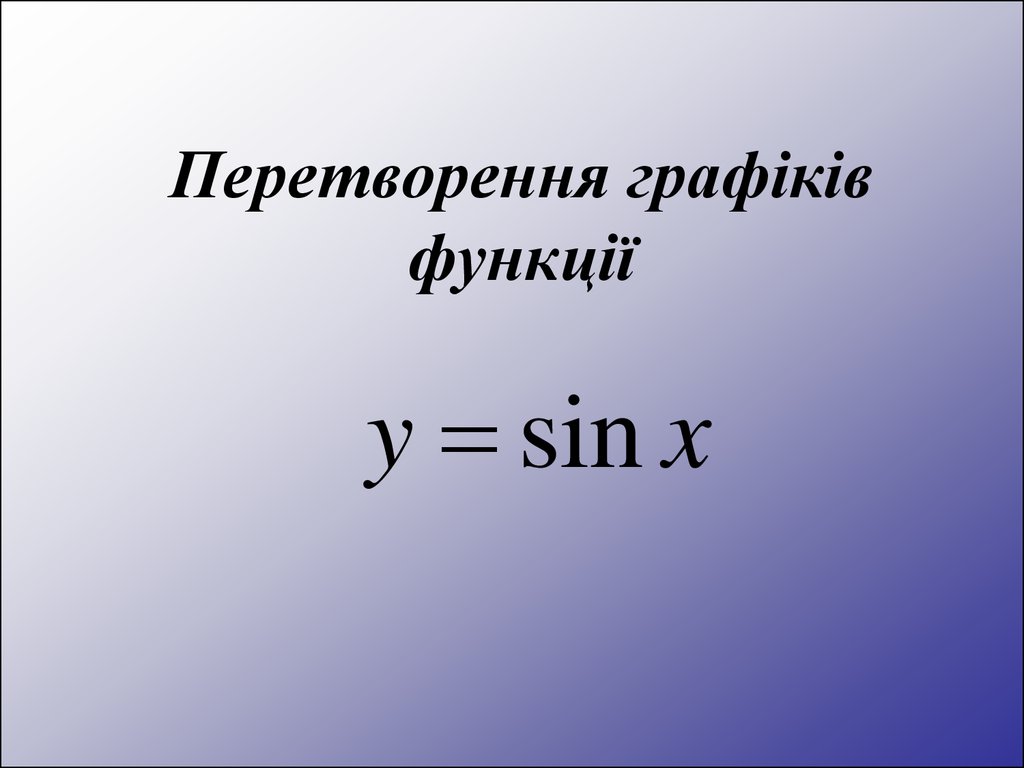


 Математика
Математика








