Производная сложной функции

1. Тема урока: "Производная сложной функции". Выполнила преподаватель математики ГАОУ СПО «АПТ»: К.Р. Абдуллина

Тема урока: "Производная
сложной функции".
Выполнила преподаватель математики
ГАОУ СПО «АПТ»: К.Р. Абдуллина

2. Цели:

образовательная:
– знать понятие сложной функции;
- уметь находить по правилу производную сложной
функции;
- изучить алгоритм вычисления производной сложной
функции;
развивающая:
- развить умение обобщать, систематизировать на основе
сравнения,
делать вывод;
- развить наглядно-действенное творческое воображение;
- развить навыки самоконтроля, умение конспектировать,
переключаться с одного вида деятельности на другой.
2

3.

воспитательная:
- воспитать чувство долга, ответственности, воли и
настойчивости для
достижения конечных результатов при нахождении
производных
сложных функций;
- формирование умения рационально, аккуратно оформить
задание на
доске и в тетради.
- воспитать умение слушать и уважать мнение других.
3

4. План урока:

1. Организационный момент. Рефлексия
настроения.
2. Обсуждение темы занятия, мотивация
обучения, целепологание.
3. Проверка домашнего задания.
4. Актуализация знаний, умений и навыков.
5. Усвоение новых знаний.
6. Закрепление изученного материала.
7. Формирование навыков.
8. Самостоятельная работа.
9. Домашнее задание.
10. Подведение итогов. Рефлексия.
4

5. Ответы

у
1 х 2 (2 х 7)
2
х
х
у 2 х 1
2
6
х
14 х
2
х
х2
х3 1
х4 2х
( х 3 1) 2
Слайд №
х 5
5х
6
5
3х 3
х
7
15
21х 4
х
6
5

6. Лист контроля

Ф.И.О
студента
Группа
Домашнее
задание
Игра
«Лото»
Тест
Итоговая
оценка
6

7. Таблица производных.

Функция
Производная
С
Х
Хn
0
1
xn 1
n
1
Х
1
х2
х
sin x
cos x
tg x
ctg x
1
2 х
cos x
-sin x
1
cos 2 x
1
sin 2 x
Функция
arcsin x
arccos x
Производная
1
1 x2
1
1 x2
arctg x
1
1 x2
arcctg x
1
1 x2
a
x
e
x
a
xlna
ex
log a x
1
xlna
Ln x
1
x
Слайд №
7

8. Тест

6 5
1. Найдите производную функции:у 9 9 x x
1 6
5
9
1) у 9 х х х ; М
2
5
7
4
2) у 9 х 72 х 5х ; П
7
4
3) у 72 х 6 х ; Л
4) у 17 х 6 х ; К
7
4
8

9.

2. Найдите производную функции: у 3х 2 сosx
1) у 6 х cos x; Е
2) у 6 х cos x 3x 2 sin x; А
3) у х3 cos x 3x 2 sin x; О
4) у 6 х cos x 3x 2 sin x;У
9

10.

3. Найдите производную функции:
у ( х 1)( х 2) ( х 1)( х 3)
1) у 7; В
2) у 7; Г
3) у 1; Д
4) у 1; М
10

11.

4. Найдите производную функции: у х 4 1
1
1) у 4 х х 2 ; Е
3
у
4
х
2)
х
1
;С
2
х
1
3) у 4 х х 2 ; Р
3
1
4) у 4 х х 2 ; А
11

12.

5. Найдите производную функции у 2 х 1
4х 2
2
1) у (2 х 1) 2 ; В
2
;А
2) у
2
(2 х 1)
2
х
3) у
;Е
2
(2 х 1)
4)
у
2х
;У
2
(2 х 1)
12

13.

6. Найти значение производной функции
2
у х sin x в х0
1) у 2 1;У
2) у 2 1; Н
3) у 2 1; П
4) у 2 ; Д
13

14.

7. Найдите f (1) , если: f ( x) 5 4e x
х
1) 9;Т.
2) 5 4e; Ж
3) 5;Р
4) 5 4e; О
14

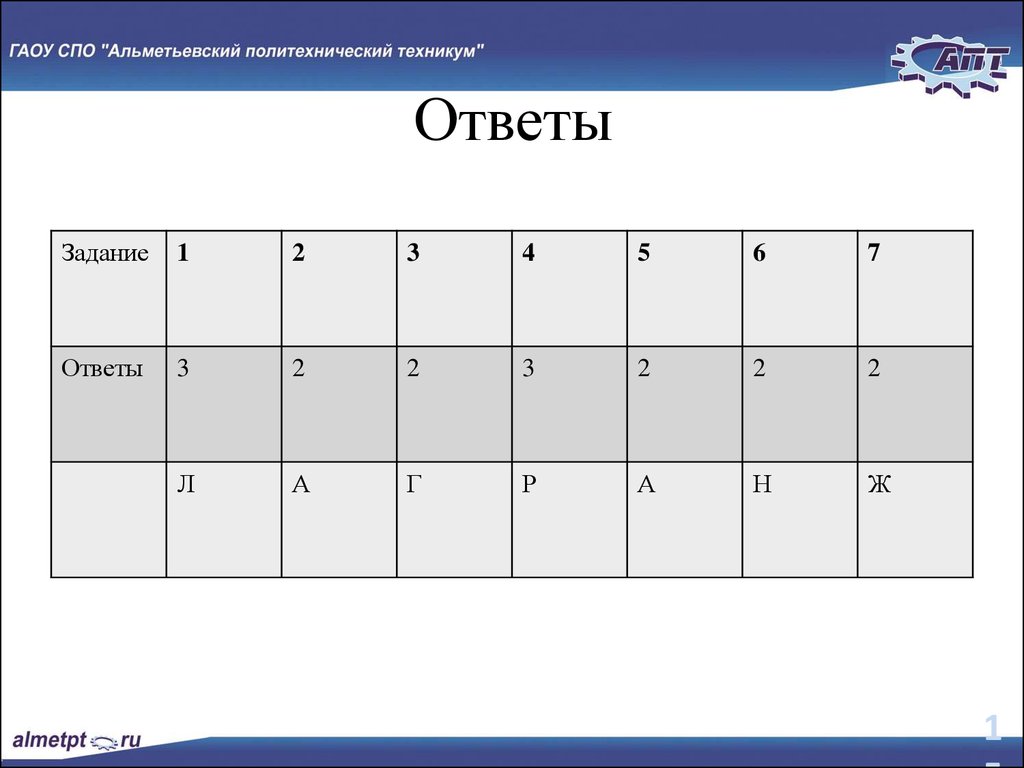
15. Ответы

Задание
1
2
3
4
5
6
7
Ответы
3
2
2
3
2
2
2
Л
А
Г
Р
А
Н
Ж
1

16.

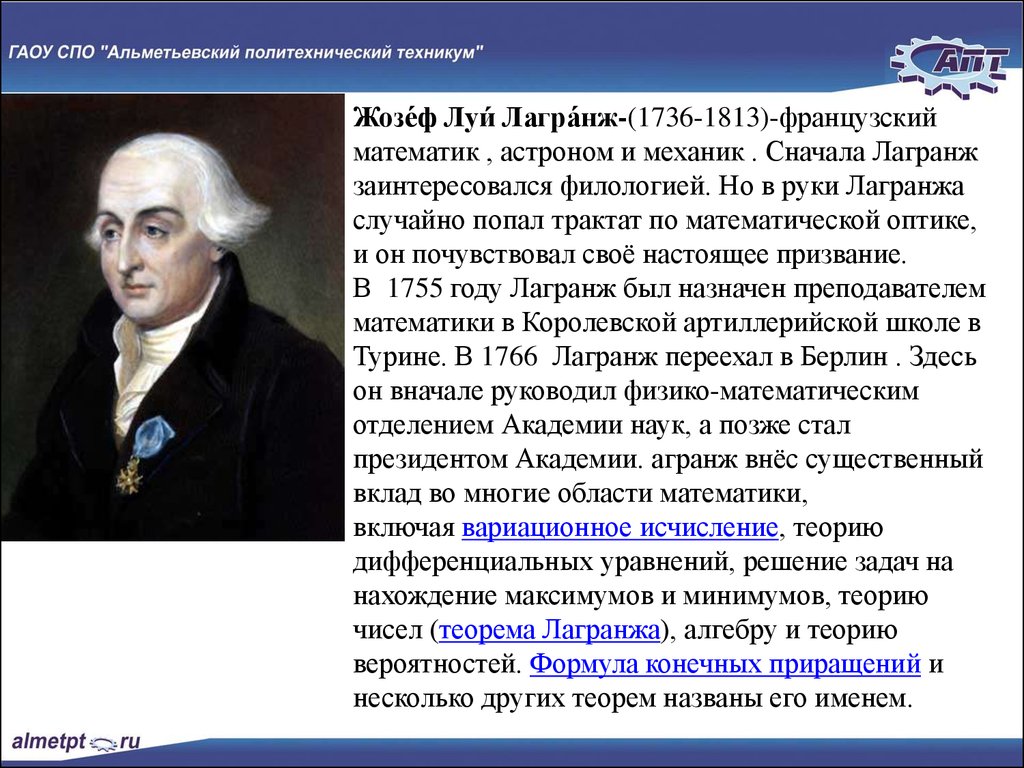
Жозе́ф Луи́ Лагра́нж-(1736-1813)-французский
математик , астроном и механик . Сначала Лагранж
заинтересовался филологией. Но в руки Лагранжа
случайно попал трактат по математической оптике,
и он почувствовал своё настоящее призвание.
В 1755 году Лагранж был назначен преподавателем
математики в Королевской артиллерийской школе в
Турине. В 1766 Лагранж переехал в Берлин . Здесь
он вначале руководил физико-математическим
отделением Академии наук, а позже стал
президентом Академии. агранж внёс существенный
вклад во многие области математики,
включая вариационное исчисление, теорию
дифференциальных уравнений, решение задач на
нахождение максимумов и минимумов, теорию
чисел (теорема Лагранжа), алгебру и теорию
вероятностей. Формула конечных приращений и
несколько других теорем названы его именем.
Слайд №
16

17. Производная сложной функции

Сложная функция: y g f x .
y f 5;
Примеры: 1) y 3 x 2 x .
2
2
5
f 3 x 2 x.
y f;
y cos f ;
3) y cos 2 x .
f sin x.
3
f 2x .
3
Правило нахождения производной сложной функции
/
/
/
g f x g f f x
2) y sin x .
(производная сложной функции равна
производной основной функции
на производную внутренней функции)
Слайд №
17

18. ПРОИЗВОДНАЯ СЛОЖНОЙ ФУНКЦИИ

Сложная функция: y g f x .
Правило нахождения производной сложной функции
(производная сложной функции равна
/
/
/
g f x g f f x производной основной функции
Простая
функция
x
Производная
простой
функции
n
1
x
x
sin x
nx
n 1
1
2
x
1
2 x
cos x
на производную внутренней функции)
Сложная функция
Производная сложной
функции
f
n
x
1
f x
f x
sin f x
Слайд №
n f n 1 x f / x
f / x
2
f x
f / x
2 f x
cos f x f / x
18

19. ПРОИЗВОДНАЯ СЛОЖНОЙ ФУНКЦИИ

Сложная функция: y g f x .
Правило нахождения производной сложной функции
g / f x g / f f / x
Простая
функция
Производная
простой
функции
(производная сложной функции равна
производной основной функции
на производную внутренней функции)
Сложная
функция
1
f x
1
x
1
2
x
1
1
Пример:
1) y
. y ;
f
sin x
f / sin x.
Производная сложной функции
/
f
x
1
/
2
f x 2
f x
f x
1
1
cos x
/
1
y
sin 2 x sin x sin 2 x cos x sin 2 x .
Слайд №
19
sin x
/

20. ПРОИЗВОДНАЯ СЛОЖНОЙ ФУНКЦИИ

Сложная функция: y g f x .
Правило нахождения производной сложной функции
сложной функции равна
g / f x g / f f / x (производная
производной основной функции
на производную внутренней функции)
Простая
функция
Производная
простой
функции
y
/
Производная сложной функции
f x
1
x
Пример:
Сложная
функция
2 x
1
2 f x
f / x
f / x
2 f x
1) y 2 x x . y f ;
f 2 x 3 x.
2x
3
3
x
4
/
1
2 2x x
3
2 x 1
3
Слайд №
/
6x2
2x 2x 1
2
3x
.
2 x 2 120

21. ПРОИЗВОДНАЯ СЛОЖНОЙ ФУНКЦИИ

Сложная функция: y g f x .
Правило нахождения производной сложной функции
сложной функции равна
g / f x g / f f / x (производная
производной основной функции
на производную внутренней функции)
Простая
функция
Производная
простой
функции
sin x
cos x
Пример:
Сложная
функция
1) y sin 2 x .
3
sin f x
Производная сложной
функции
cos f x f / x
y sin f ;
f 2x .
3 /
y sin 2 x cos 2 x 2 x 2 cos 2 x .
3
3
3
3
/
/
Слайд №
21

22. ПРОИЗВОДНАЯ СЛОЖНОЙ ФУНКЦИИ

Простая
функция
x
n
Производная
простой
функции
nx n 1
Сложная
функция
f n x
Производная сложной функции
n f n 1 x f / x
f / x
2
f x
f / x
1
x
1
2
x
1
f x
x
2 x
f x
cos x
sin f x
cos f x f / x
cos x
sin x
cos f x
sin f x f / x
tgx
1
2
cos x
sin x
1
tgf x
Слайд №
2 f x
/
f
x
1
/
f x
2
cos f x
cos 2 f 22x

23. Закрепление изученного материала.

Вычислите производные:
4
у
(
x
3
)
1)
2) у ( х3 х 2 11)3
3) у sin( 5 x 3)
4) у cos10 x
5) у tg 4 x
6)
Слайд №
у х2 1
23

24. Домашнее задание.

• Выучить алгоритм.
• Найти производную.
8
у
(
2
3
х
)
«3» 2
у
5
х
3
«4» -
«5» - у (2 х 3) 4
Слайд №
24

25.

Подведение итогов урока, рефлексия:
- сдача листов контроля;
- рефлексия.
Вам предлагается каждому для себя ответить на
следующие вопросы:
-Что вы узнали нового?
-Смогли бы вы объяснить новый материал другу?
-Над чем вам надо еще поработать в данной теме?
-Какой вопрос сегодняшнего урока был самым трудным?
-Поставьте оценки по пятибалльной шкале за работу на
уроке
а) себе, оценив свою активность на уроке,
самостоятельность, правильность выполнения заданий.
б) классу,
в) учителю.
Слайд №
25

26.

Спасибо за
урок.
Слайд №
26