Детали машин. Курсовое проектирование

1.

Детали машин
Курсовое проектирование
В.И. Капустин, К.В. Захарченко
НГТУ
Новосибирск

2.

ВЫПОЛНЕНИЕ РАСЧЁТОВ
В соответствии с ГОСТ 2.106 расчёт должен содержать:
1. Цель расчёта.
2. Условия расчёта и исходные данные. В соответствии с
этим требованием в каждом разделе должен быть пункт
«Исходные данные».
3. Расчётную схему. Например, в расчётах передач
необходимо приводить кинематическую схему по ГОСТ
2.703 с элементами по ГОСТ 2.770;иногда в двух проекциях;
другие разделы также могут содержать эскизы и схемы.
4. Расчёт. Последовательность либо алгоритм расчёта
должны приводиться с обозначениями пунктов. Расчет
должен быть «прозрачным» т.е. доступным для проверки.
5. Выводы.

3.

Контрольное задание № 6
4.10. Проверочные расчеты валов
4.10.1. Проверка статической прочности
4.10.2 Проверочный расчет вала на сопротивление усталости
План
1. Дано: эскиз вала, исходя из приложенных к нему
внешних нагрузок (сил и моментов) и габаритов сборочной единицы,
в которой проектируемый вал должен быть установлен.
На эскизе указано предварительно выбранные диаметры и длины
отдельных участков, полную длину вала
2. Составляем расчетную схему нагружения вала в двух взаимно
перпендикулярных плоскостях (горизонтальной X и вертикальной Y),
представляя его как балку, шарнирно закрепленную в двух жестких
опорах. При этом считают, что установленные на вал детали передают
силы и моменты на середине своей ширины

4.

Контрольное задание № 6
4.10. Проверочные расчеты валов
4.10.1. Проверка статической прочности
4.10.2 Проверочный расчет вала на сопротивление усталости
План
3. По правилам, известным из курса «Сопротивление материалов»,
определяем реакции опор, строим эпюры изгибающих моментов в
каждой плоскости, и отдельно - эпюру крутящего момента.
На основании эпюр намечаем положение опасных сечений, учитывая
при этом диаметры вала и влияние концентраторов напряжений.
4. Проверяем статическую прочность вала и выполняем расчет на
сопротивление усталости
Внешние нагрузки передаются на валы через установленные на
них детали, поэтому величины нагрузок определяют при расчете этих
деталей

5.

Контрольное задание № 6
4.10. Проверочные расчеты валов
4.10.1. Проверка статической прочности
Пример
Выполнить расчет ведущего вала одноступенчатого цилиндрического
косозубого редуктора по следующим данным:
передаваемая валом мощность Р1 = 9,5 кВт;
угловая скорость ω1 = 100 рад/с;
материал вала – сталь 45, термическая обработка – улучшение
На валу установлена шестерня с делительным диаметром d1 = 110 мм,
ширина шестерни b1 = lст = 100 мм, угол наклона зубьев β = 10 ͦ
К выходному концу вала приложена дополнительная нагрузка Fм от
муфты
Эскиз вала показан на рис. а

6.

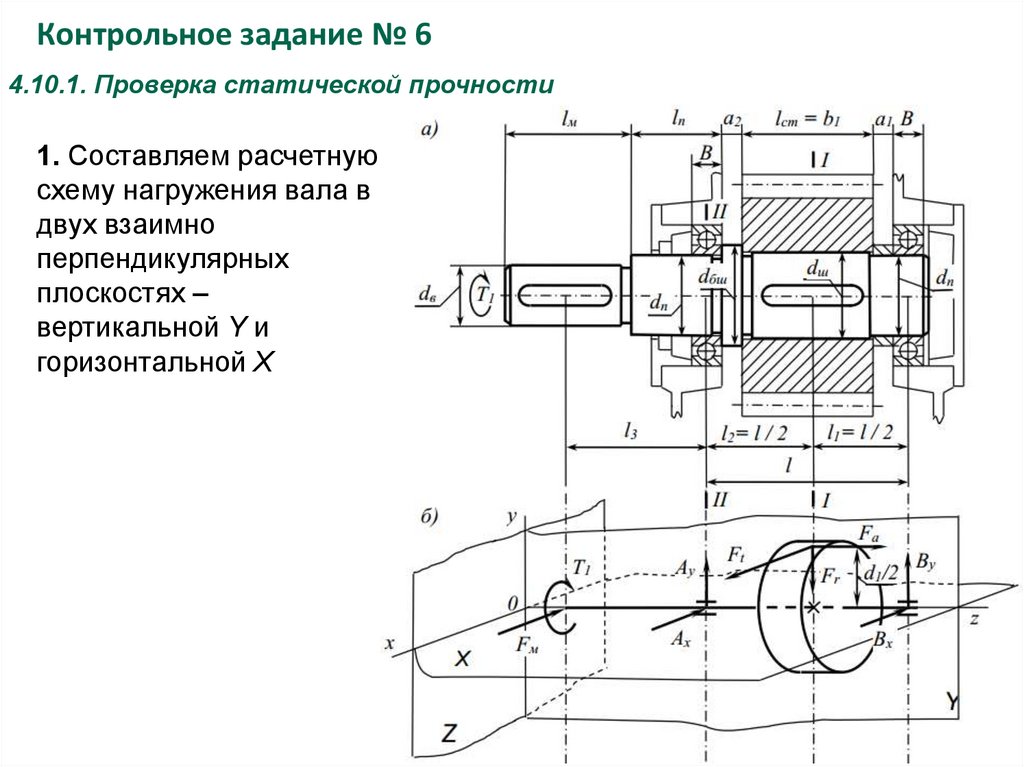
Контрольное задание № 6
4.10.1. Проверка статической прочности
1. Составляем расчетную
схему нагружения вала в
двух взаимно
перпендикулярных
плоскостях –
вертикальной Y и
горизонтальной X

7.

Контрольное задание № 6
4.10.1. Проверка статической прочности
2. Передаваемый валом момент Т1 уже определен (см. КЗ 2)
3. Внешние нагрузки, действующие на вал:
а) Силы в зацеплении, определенные при расчете зубчатой передачи:
окружная
радиальная
где α – угол зацепления, для зубчатых колес без смещения или
равносмещенных α = 20 ͦ
осевая
б) Нагрузка от муфты или другого устройства:

8.

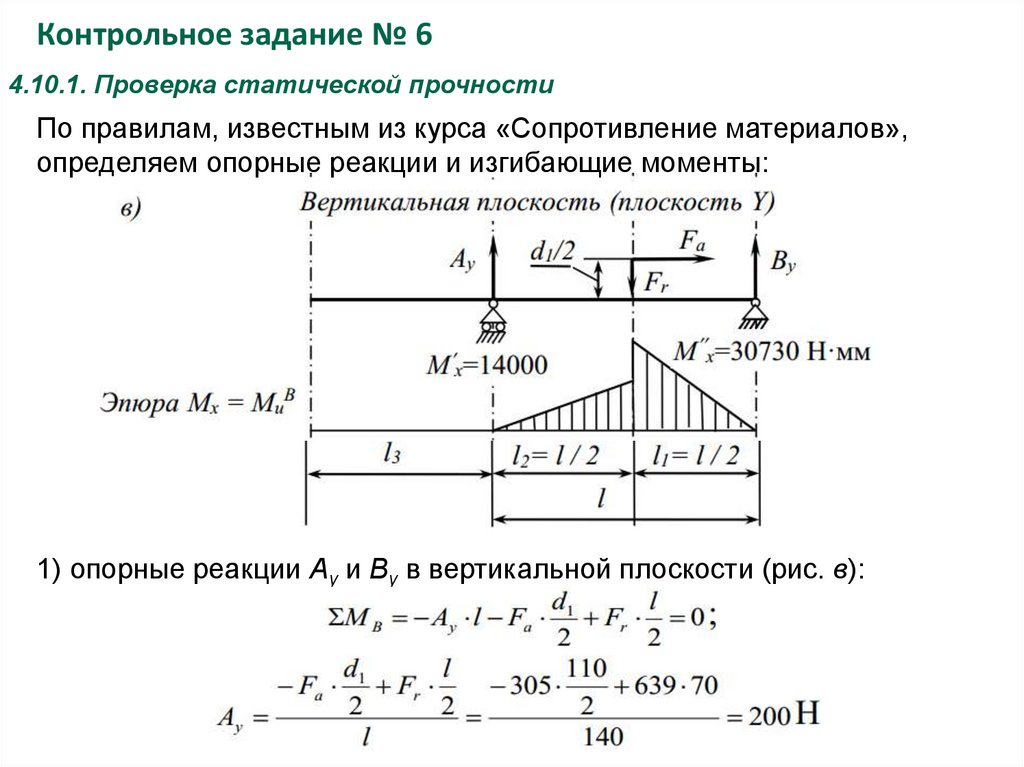
Контрольное задание № 6
4.10.1. Проверка статической прочности
По правилам, известным из курса «Сопротивление материалов»,
определяем опорные реакции и изгибающие моменты:
1) опорные реакции Ay и By в вертикальной плоскости (рис. в):

9.

Контрольное задание № 6
4.10.1. Проверка статической прочности
1) опорные реакции Ay и By в вертикальной плоскости (рис. в):
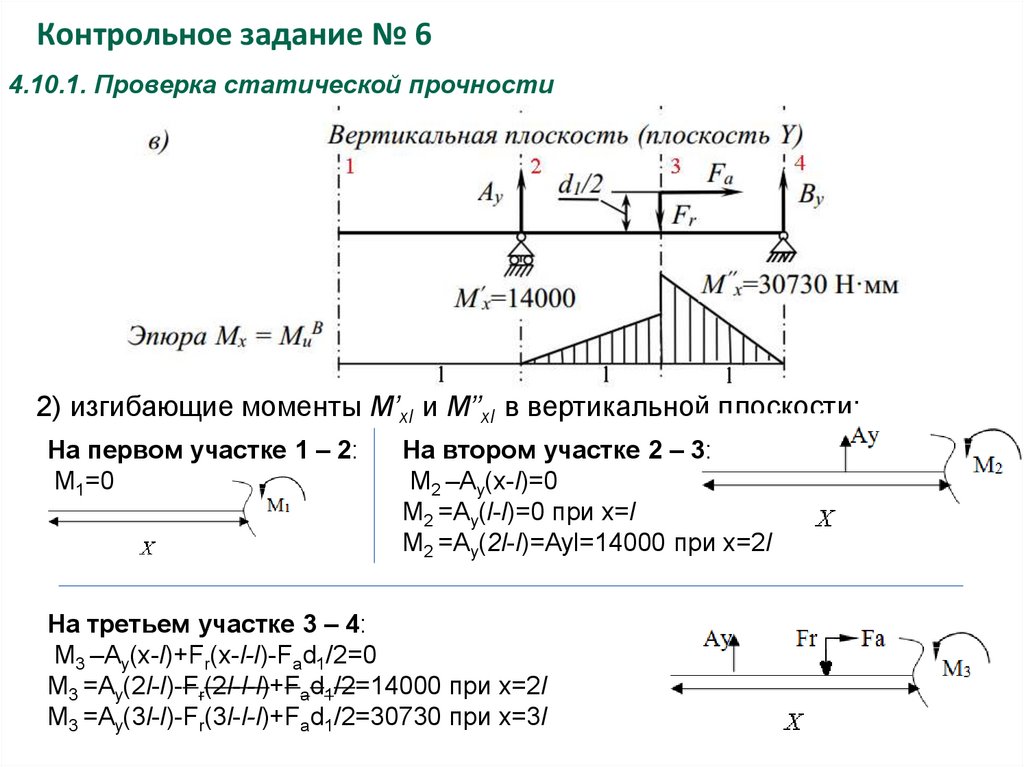
2) изгибающие моменты M’xI и M’’xI в вертикальной плоскости:

10.

Контрольное задание № 6
4.10.1. Проверка статической прочности
2) изгибающие моменты M’xI и M’’xI в вертикальной плоскости:
На первом участке 1 – 2:
M1=0
На втором участке 2 – 3:
M2 –Ау(x-l)=0
M2 =Ау(l-l)=0 при x=l
M2 =Ау(2l-l)=Ayl=14000 при x=2l
На третьем участке 3 – 4:
M3 –Ау(x-l)+Fr(x-l-l)-Fad1/2=0
M3 =Ау(2l-l)-Fr(2l-l-l)+Fad1/2=14000 при x=2l
M3 =Ау(3l-l)-Fr(3l-l-l)+Fad1/2=30730 при x=3l

11.

Контрольное задание № 6
4.10.1. Проверка статической прочности
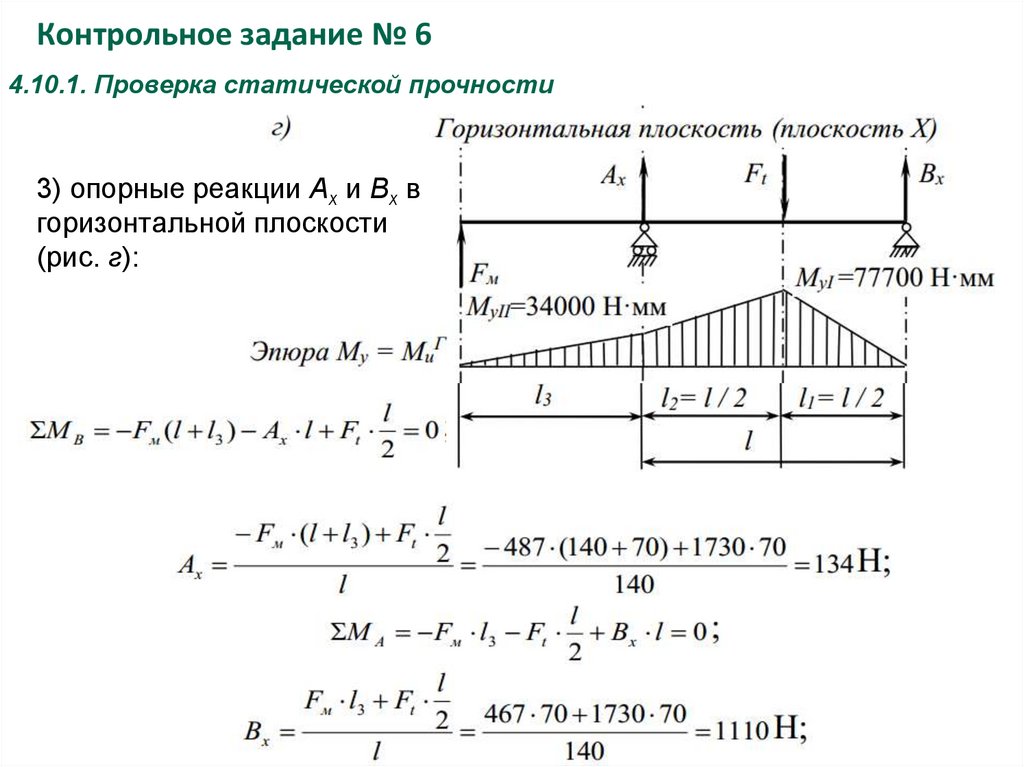
3) опорные реакции Ax и Bx в
горизонтальной плоскости
(рис. г):

12.

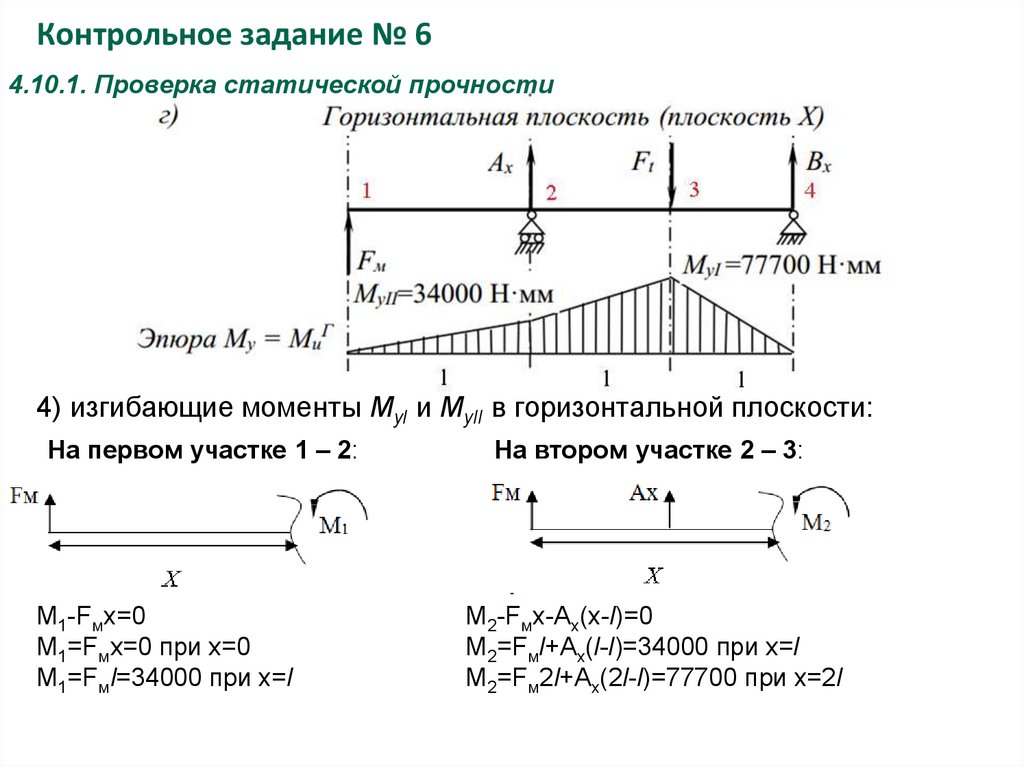
Контрольное задание № 6
4.10.1. Проверка статической прочности
4) изгибающие моменты MyI и MyII в горизонтальной плоскости:
На первом участке 1 – 2:
M1-Fмx=0
M1=Fмx=0 при x=0
M1=Fмl=34000 при x=l
На втором участке 2 – 3:
M2-Fмx-Ax(x-l)=0
M2=Fмl+Ax(l-l)=34000 при x=l
M2=Fм2l+Ax(2l-l)=77700 при x=2l

13.

Контрольное задание № 6
4.10.1. Проверка статической прочности
4) изгибающие моменты MyI и MyII в горизонтальной плоскости:
На третьем участке 3 – 4:
M3-Fмx-Ax(x-l)+Ft(x-2l)=0
M3=Fм2l+Ax(2l-l) -Ft(2l-2l)=77700 при x=2l
M3=Fм3l+Ax(3l-l)-Ft(3l-2l)=0 при x=3l

14.

Контрольное задание № 6
4.10.1. Проверка статической прочности
4. Результирующий изгибающий момент M в сечении I-I:
5. Реакции в опорах:
6. Передаваемый валом крутящий момент действует относительно оси
z и обозначается Mz. В рассматриваемом примере Mz = Мк = T1 (рис. д)

15.

Контрольное задание № 6
4.10.1. Проверка статической прочности
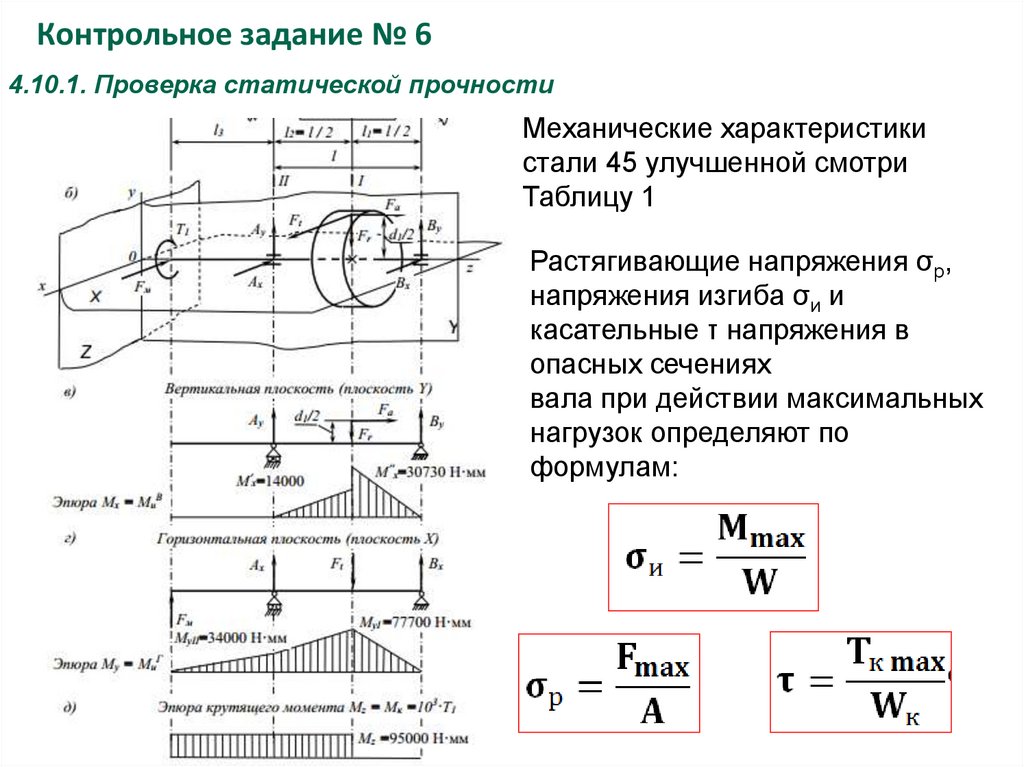
Механические характеристики
стали 45 улучшенной смотри
Таблицу 1
Растягивающие напряжения σр,
напряжения изгиба σи и
касательные τ напряжения в
опасных сечениях
вала при действии максимальных
нагрузок определяют по
формулам:

16.

Контрольное задание № 6
4.10.1. Проверка статической прочности
где Mmax – наибольший суммарный изгибающий момент, Н·мм
Fmax – наибольшая осевая сила, Н, Fmax = Kп · Fa
Tк max – наибольший крутящий момент, Н·мм
Tк max = 1000·Tmax = 1000·Kп ·T
Kп – коэффициент перегрузки
T – номинальный вращающий
момент, Н·м
А – площадь поперечного сечения
вала, мм2
W и Wк – моменты
сопротивления сечения вала
при расчете на
изгиб и кручение, мм3

17.

Контрольное задание № 6
4.10.1. Проверка статической прочности
7. Находим эксвивалентное напряжение по IV теории прочности,
которое должно удовлетворять неравенству:
Таблица 1

18.

Контрольное задание № 6
4.10.1. Проверка статической прочности
Характерные ошибки:
1. Неправильно выполнена расчетная схема вала в соответствии с силовой
схемой нагружения валов.
2. Неправильно составлены уравнения равновесия и уравнения
изгибающих моментов. Ошибка в знаках моментов и проекций.
3. Несоразмерность единиц моментов и длин участков вала при расчетах.
4. Неправильные вычисления.
5. Не соблюдены требования ЕСКД при выполнении расчетной схемы и
эпюр в изометрии.
6. Неточно составлены схемы нагружения подшипников.
________________________________________________________________
* Масштаб эпюры моментов μ Н·м/мм, определяется отдельно для каждой
эпюры в зависимости от значения момента (М, Т) и показывает количество
Н·м в 1 мм эпюры

19.

Контрольное задание № 6
4.10.1. Проверка статической прочности

20.

Контрольное задание № 6
4.9.1. Проверка статической прочности

21.

Контрольное задание № 6
4.10.2 Проверочный расчет вала на сопротивление усталости
Расчетом определяют коэффициент S запаса прочности для каждого
предварительно намеченного опасного сечения и сравнивают его
с минимально допустимым значением:
где [S] – минимально допустимое значение коэффициента запаса
прочности, принимаемое в зависимости от ответственности
конструкции и последствий разрушения вала, точности определения
нагрузок и напряжений, технологии изготовления и контроля. Обычно
[S] = 1,5…2,5
Коэффициент запаса прочности вычисляют по формуле:
где Sσ и Sτ – коэффициенты запаса прочности по нормальным и
касательным напряжениям

22.

Контрольное задание № 6
4.10.2 Проверочный расчет вала на сопротивление усталости
Sσ и Sτ – коэффициенты запаса прочности по нормальным и
касательным напряжениям, определяемые в общем случае по
соотношениям:
(Формулы 1, 2)
где σ-1D и τ-1D – пределы выносливости материала вала в
рассматриваемом сечении, МПа
σa и τa – амплитуды напряжений цикла, МПа
σm и τm – средние напряжения цикла, МПа

23.

Контрольное задание № 6
4.10.2 Проверочный расчет вала на сопротивление усталости
При расчете на сопротивление усталости считают, что нормальные
напряжения (напряжения изгиба) изменяются по симметричному
циклу (а), а касательные (напряжения кручения) – по отнулевому (б)
В этом случае:
Тогда формулы 1 и 2:

24.

Контрольное задание № 6
4.10.2 Проверочный расчет вала на сопротивление усталости
Пределы выносливости вычисляют для каждого рассматриваемого
опасного сечения:
где σ-1 и τ-1 – пределы выносливости гладких образцов при
симметричном цикле изгиба и кручения, МПа
KσD и KτD – коэффициенты снижения предела выносливости,
определяемые по зависимостям:
Если в рассматриваемом расчетном сечении имеется несколько
концентраторов напряжений, учитывают только наиболее опасный из
них (для которого KσD и KτD имеют наибольшее значение)

25.

Контрольное задание № 6
4.10.2 Проверочный расчет вала на сопротивление усталости
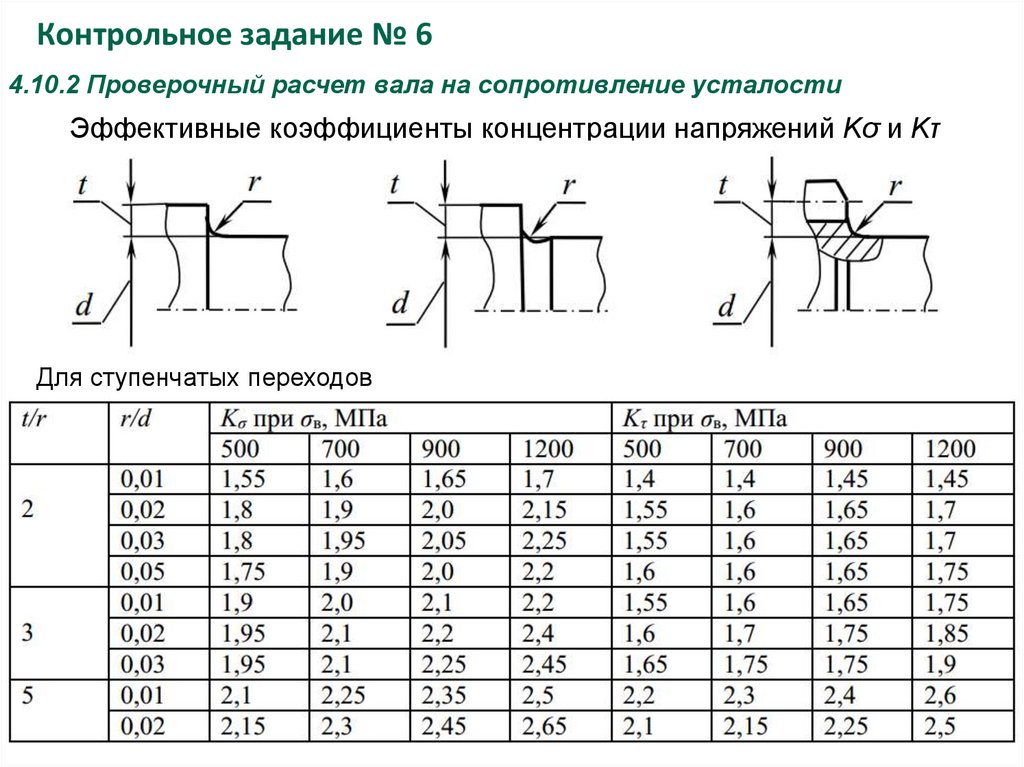
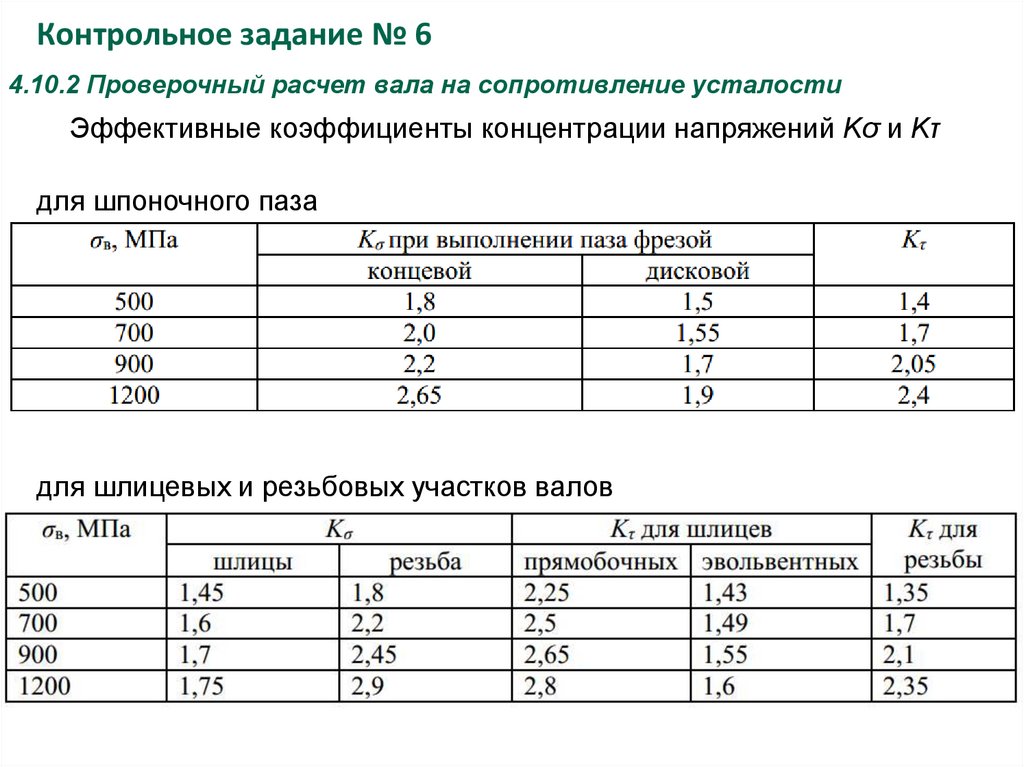
Эффективные коэффициенты концентрации напряжений Kσ и Kτ
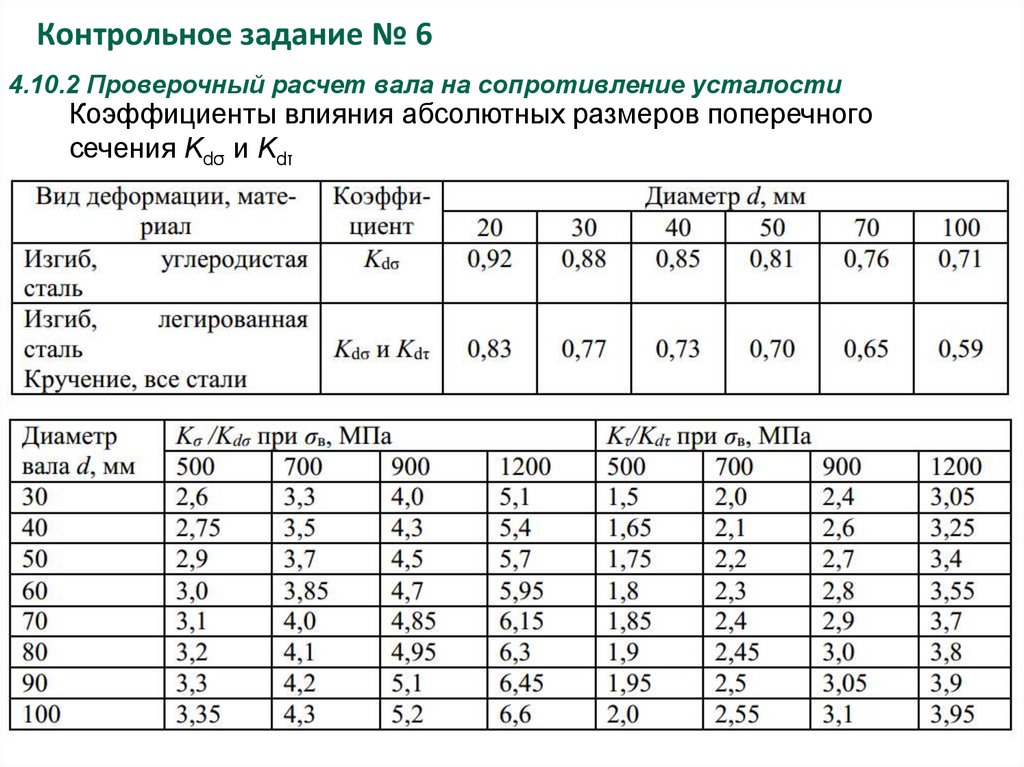
Коэффициенты влияния абсолютных размеров поперечного
сечения Kdσ и Kdτ
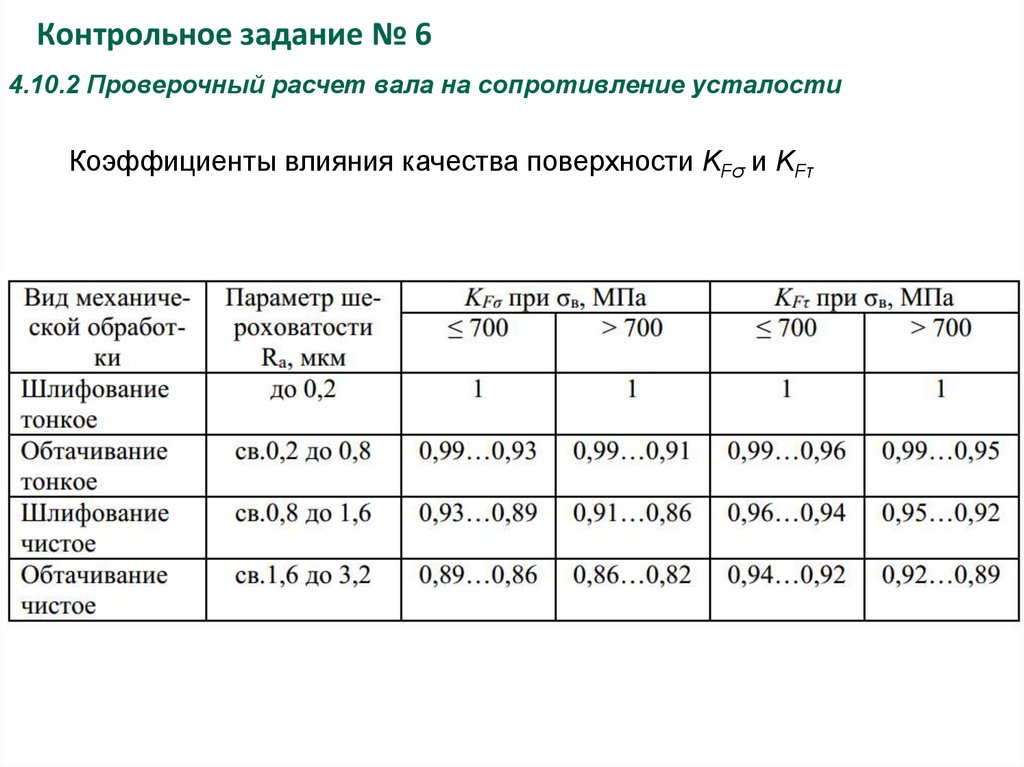
Коэффициенты влияния качества поверхности KFσ и KFτ
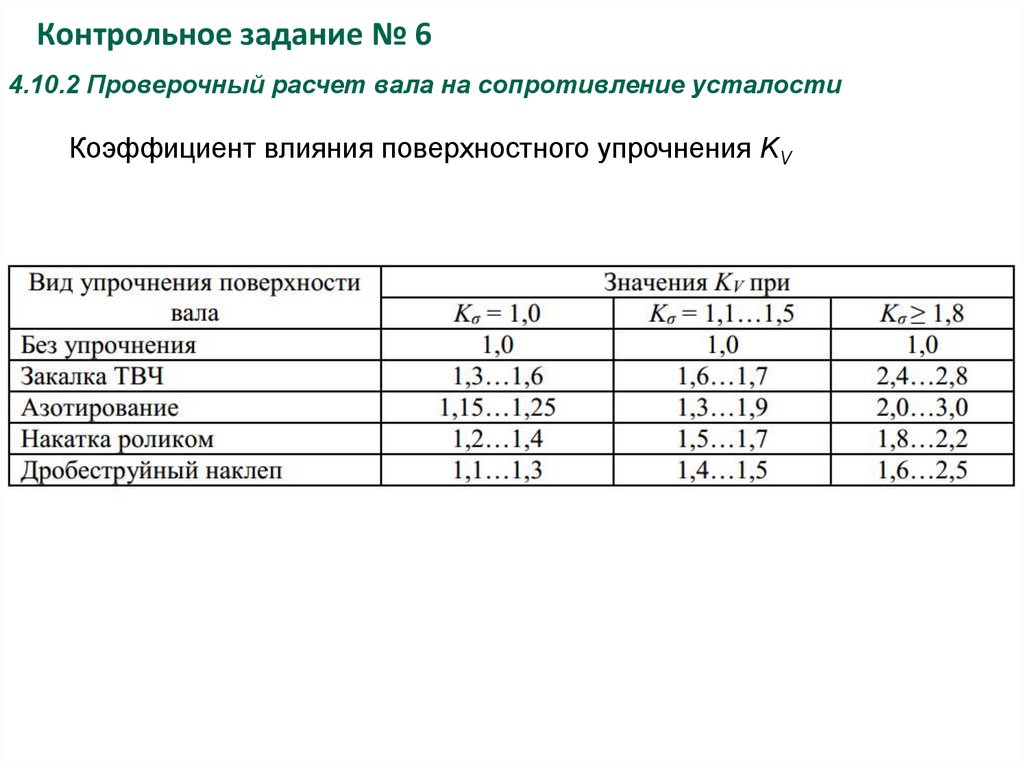
Коэффициент влияния поверхностного упрочнения KV
Коэффициент влияния асимметрии цикла ψτD вычисляют по
формуле:
где ψτ – коэффициент чувствительности материала к асимметрии
цикла напряжений

26.

Контрольное задание № 6
4.10.2 Проверочный расчет вала на сопротивление усталости
Эффективные коэффициенты концентрации напряжений Kσ и Kτ
Для ступенчатых переходов

27.

Контрольное задание № 6
4.10.2 Проверочный расчет вала на сопротивление усталости
Эффективные коэффициенты концентрации напряжений Kσ и Kτ
для шпоночного паза
для шлицевых и резьбовых участков валов

28.

Контрольное задание № 6
4.10.2 Проверочный расчет вала на сопротивление усталости
Коэффициенты влияния абсолютных размеров поперечного
сечения Kdσ и Kdτ

29.

Контрольное задание № 6
4.10.2 Проверочный расчет вала на сопротивление усталости
Коэффициенты влияния качества поверхности KFσ и KFτ

30.

Контрольное задание № 6
4.10.2 Проверочный расчет вала на сопротивление усталости
Коэффициент влияния поверхностного упрочнения KV

31.

Заключение
Спасибо за внимание!