Последовательное, параллельное и смешанное соединение сопротивлений

1.

2.

1. Последовательное соединение
пассивных элементов цепи.
2. Параллельное соединение
пассивных элементов цепи.
3. Смешанное соединение пассивных
элементов цепи.

3.

Последовательным
соединением
резисторов называется такое соединение их
выводов, при котором по всем резисторам
проходит один и тот же ток; пример такого
соединения показан на рис. 1.
Рис. 1. Последовательное
соединение резисторов

4.

Согласно закону Ома напряжение на
резисторах в схеме на рас. 1 равны
соответственно: U1 = R1 ∙ I; U2 = R2 ∙ I; U3 = R3 ∙ I.
Сопротивление R = R1 + R2 + R3 – это общее
или эквивалентное сопротивление цепи при
последовательном
соединении
резисторов.
Эквивалентным называют сопротивление
такого резистора (участка цепи), замена которым
действительных резисторов в схеме не вызовет
изменения тока (токов) и напряжения (напряжений)
в преобразованной части цепи.

5.

Пример 1. Три резистора с сопротивлением:
R1 = 20 Ом, R2 = 25 Ом, R3 = 5 Ом соединены
последовательно и подключены к источнику с
напряжением U = 100 B. Определить напряжение на
резисторах, их мощности и общую мощность.
Решение. Эквивалентное сопротивление цепи:
R = R1 + R2 + R3 = 20 + 25 + 5 = 50 Ом.
По закону Ома ток I = U / R = 100 / 50 = 2 А.
Напряжение на резисторах:
U1 = R1 ∙ I = 20 ∙ 2 = 40 В;
U2 = R2 ∙ I = 25 ∙ 2 = 50 В;
U3 = R3 ∙ I = 5 ∙ 2 = 10 В.

6.

Сумма этих напряжений равна напряжению на
общих выводах, т.е. выводах источника питания
цепи: U = U1 + U2 + U3 = 40 +50 +10 = 100 B.
Мощности участков цепи: P1 = R1 ∙ I2 = 20 ∙ 22
= 80 Bт; P2 = R2 ∙ I2 = 25 ∙ 22 = 100 Bт;
P3 = R3 ∙ I2 = 5 ∙ 22 = 20 Bт
Общая мощность:
P = P1 + P2 + P3 = 80 + 100 + 20 = 200 Вт.

7. 2. Параллельное соединение пассивных элементов цепи

При параллельном соединении все резисторы
подключаются к одним и тем же двум узлам цепи и,
следовательно, находятся под одним и тем же
напряжением; пример такого соединения показан на
рис. 2, где UАБ = U. Параллельно соединенные ветви
имеют две общие точки – узлы А и Б, в которых
сходятся ветви с сопротивлениями резисторов R1,
R2, R3.
Согласно первому закону Кирхгофа ток I в
неразветвленной части цепи равен сумме токов в
резисторах: I = I1 + I2 + I3.

8.

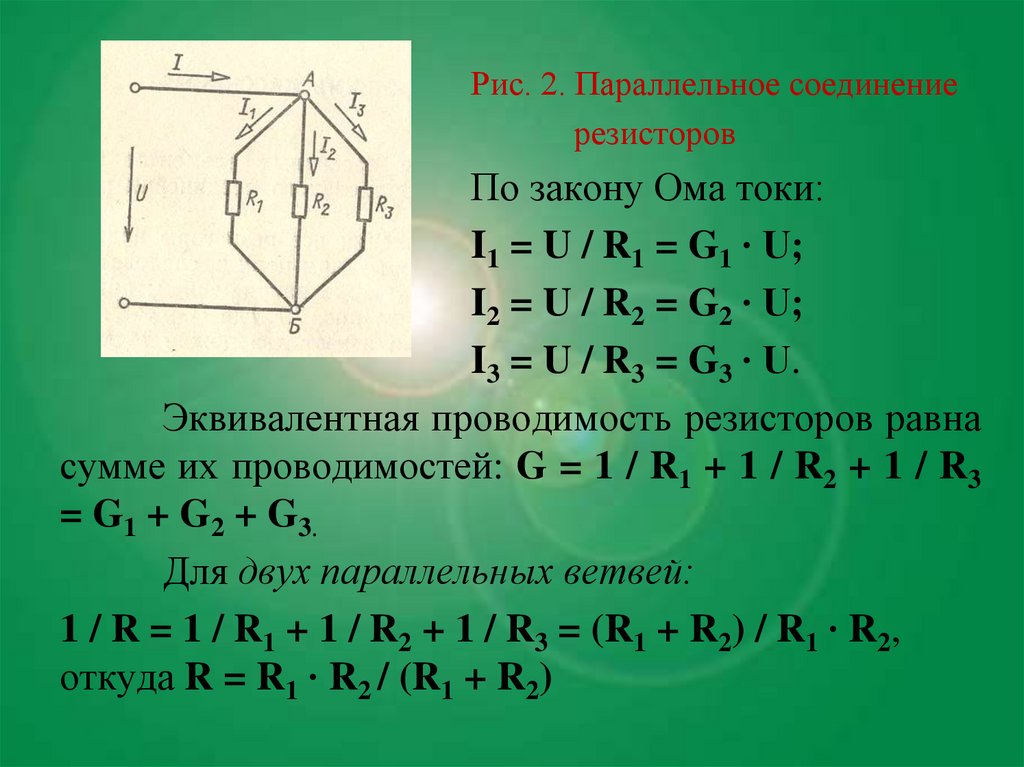
Рис. 2. Параллельное соединение
резисторов
По закону Ома токи:
I1 = U / R1 = G1 ∙ U;
I2 = U / R2 = G2 ∙ U;
I3 = U / R3 = G3 ∙ U.
Эквивалентная проводимость резисторов равна
сумме их проводимостей: G = 1 / R1 + 1 / R2 + 1 / R3
= G1 + G2 + G3.
Для двух параллельных ветвей:
1 / R = 1 / R1 + 1 / R2 + 1 / R3 = (R1 + R2) / R1 ∙ R2,
откуда R = R1 ∙ R2 / (R1 + R2)

9.

Так как мощность участка цепи (закон
Джоуля-Ленца) : P = R ∙ I2 = R ∙ (U / R)2 = G ∙ U, то
P1 = G1 ∙ U2; P2 = G2 ∙ U2; P3 = G3 ∙ U2,
где P1, P2, P3 – мощности параллельно соединенных
резисторов.
Мощность параллельного соединения в
соответствии с законом сохранения энергии равна
сумме мощностей отдельных ветвей:
Р = U ∙ I = U (I1 + I2 + I3) = Р1 + Р2 + Р3.
Благодаря
своей
надежности
схема
параллельного соединения является основной
схемой электроснабжения приемников энергии.

10.

Пример 2. Параллельно соединенные три
резистора, сопротивления которых: R1 = 20 Ом, R2 =
25 Ом, R3 = 100. Определить их эквивалентное
сопротивление.
Решение. Определяем проводимости резисторов:
G1 = 1 / R1 = 1 / 20 = 0,05 См;
G2 = 1 / R2 = 1 / 25 = 0,04 См;
G3 = 1 / R3 = 1 / 100 = 0,01 См.
Эквивалентная проводимость:
G = G1 + G2 + G3 = 0,05 + 0,04 + 0,01 = 0,1 См.
Затем
определяем
их
эквивалентное
сопротивление как величину, обратную эквив-ой
проводимости: R = 1 / G = 1 / 0,1 = 10 Ом.

11. 3. Смешанное соединение пассивных элементов цепи

Смешанное
соединение
элементов
электрической цепи представляет собой сочетание
их последовательного и параллельного соединения.
Схемы
смешанного
соединения
элементов
электрической
цепи
могут
быть
самыми
разнообразными.

12.

Пример 3. Определить токи в участках цепи,
схема замещения которой изображена на рис. 3, а,
напряжения на участках и мощности, а также
мощность всей цепи, если напряжение на выводах а
– г источника питания, т.е. на входе пассивных
участков цепи, U = 50 B, а сопротивления участков
R1 = 10 Ом, R2 = 40 Ом, R3 = 60 Ом, R4 = 16 Ом.
Решение. В рассматриваемом примере
требуется определить следующие величины: I1, I2,
I3, I4, U1, U2, U3, U4, P1, P2, P3, P4, P. Токи I1 и I2
равны между собой и равны току источника
питания. Для определения этого тока по заданному
напряжению необходимо знать эквивалентное
сопротивление цепи между выводами а – г.

13.

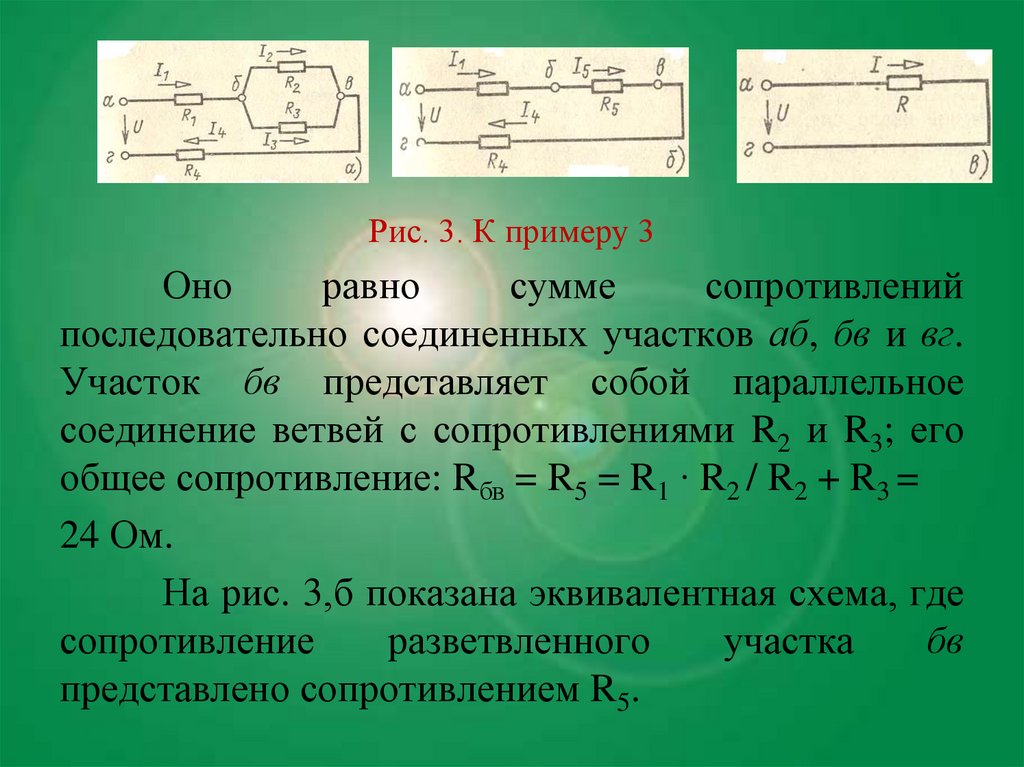
Рис. 3. К примеру 3
Оно
равно
сумме
сопротивлений
последовательно соединенных участков аб, бв и вг.
Участок бв представляет собой параллельное
соединение ветвей с сопротивлениями R2 и R3; его
общее сопротивление: Rбв = R5 = R1 ∙ R2 / R2 + R3 =
24 Ом.
На рис. 3,б показана эквивалентная схема, где
сопротивление
разветвленного
участка
бв
представлено сопротивлением R5.

14.

На схеме на рис. 4.3,б последовательно
соединены участки с сопротивлениями R1, R5 и R4.
Общее сопротивление:
R = R1 + R5 + R4 = 10 + 24 + 16 = 50 Ом.
Эквивалентная схема с сопротивлением R
показана на рис. 3, в.
По закону Ома находим токи:
I = I1 = I4 = I5 = U / R = 50 / 50 = 1 А.
Напряжение на участках цепи :
Uаб = U1 = R1 ∙ I1 = 10 ∙ 1 = 10 B;
Uбв = U5 = R5 ∙ I5 = 24 ∙ 1 = 24 B;
Uвг = U4 = R4 ∙ I4 = 16 ∙ 1 = 16 B.

15.

Напряжение Uбв = 24 В представляет собой
напряжение на любой из ветвей с сопротивлениями
R2 и R3, т.е. Uбв = U2 = U3 = 24 В.
Токи I3 = U3 / R3 = 0,4 А;I2 = U2 / R2 = 0,6 А.
Сумма токов в параллельных ветвях согласно
первому закону Кирхгофа должна быть равна току в
неразветвленной части цепи: I = I2 + I3 = 1 А.
Мощность участков цепи:
Р1 = R1 ∙ I12 = 10 ∙ 12 = 10 Вт;
Р2 = R2 ∙ I22 = 40 ∙ 0,62 = 14,4 Вт;
Р3 = R3 ∙ I32 = 60 ∙ 0,42 = 9,6 Вт;
Р4 = R4 ∙ I42 = 16 ∙ 12 = 16 Вт.

16.

Мощность всей цепи равна сумме мощностей
ее участков:
Р = Р1 + Р2 + Р3 + Р4 = 10 + 14,4 + 9,6 + 16 = 50 Вт.

17. Контрольные вопросы

1.
Назовите
отличительный
признак
последовательного соединения резисторов.
2. Чему равно эквивалентное сопротивление цепи
при последовательном соединении резисторов?
3. Как распределяются электрические напряжения
на участках цепи при последовательном соединении
резисторов?
4. Чему равны ЭДС батареи последовательно
соединенных аккумуляторов и ее внутреннее
сопротивление?

18. Контрольные вопросы

5. Какая диаграмма называется потенциальной? Как
строится потенциальная диаграмма.
6. Назовите отличительный признак параллельного
соединения резисторов.
7. Чему равна эквивалентная проводимость цепи
при параллельном соединении резисторов?
8. Как в общем случае определяется эквивалентное
сопротивление цепи при параллельном соединении
резисторов?
9. Как распределяются токи в ветвях цепи при
параллельном соединении резисторов?

19. Задачи

1. В последовательно соединенных трех резисторах,
сопротивления которых 10, 20 и 30 Ом, ток равен 2
А. Определите напряжение на выводах соединения.
2. Определите эквивалентное сопротивление
параллельного соединения четырех резисторов с
сопротивлениями 5 Ом, 10 Ом, 15 Ом и 20 Ом.
3. Приемник энергии питается от батареи из трех
аккумуляторов,
соединенных
параллельно.
Определите ток в приемнике с сопротивлением 0,9
Ом, если ЭДС одного аккумулятора равна 1,82 В, а
его внутреннее сопротивление равно 0,03 Ом.

20. Задачи

4. Приемник энергии питается от батареи из трех
аккумуляторов, соединенных последовательно.
Определите ток
в
приемнике, если
его
сопротивление 5,34 Ом, ЭДС одного аккумулятора
1,8 В и внутреннее сопротивление 0,02 Ом.
5. Три резистора, сопротивления которых R1 = 10
Ом, R2 = 20 Ом,
R3 = 30 Ом, соединены
последовательно. Определите напряжение на
выводах цепи, если напряжение на резисторе R2
равно 10 В.