Похожие презентации:
Целые уравнения и способы их решения
1. Целые уравнения и способы их решения
2. Целые уравнения и способы их решения
I.Найди ошибки и недочеты в решениях примеровПример1
х( х 4)( х 5)( х 9) 96 0,
( х 2 9 х)( х 2 9 х 20) 96 0,
х2 9х t,
t (t 20) 96,
t 2 20t 96 0,
D1 100 96 4.
t 10 2,
t1 12, t 2 8
Ответ : 12; 8
3.
Пример 2( y 2 y 4) 6( y 2 y 4) 5 0,
2
2
2
( y 2) 4 6( y 2) 2 5 0,
a b c 0,
( y 2) 2 1, ( y 2) 2 5,
y 2 1, y 2 5 ,
y 1, y 2 5.
Ответ : 1; 2 5.
4.
Пример 3( x 2 x 1) 2 6( x 2 x 1) 7 0,
x x 1 1, x x 1 7,
2
2
x 2 x 2 0, x 2 x 8 0,
D 1 8 0, D 1 32 0.
Ø
Ø
Ответ:Ø
Пример 4
x 2 x 3 0,
3
a b c 0,
x 3, x 1.
Ответ : 3;1.
5.
II. Рассмотрите уравнения:1) 24 x 4 16 x 3 3 x 2 0,
☻ 2) x 4 5 x 3 6 x 2 5 x 1 0,
3) x 4 11x 3 35 x 2 31x 6 0,
☻ 4) x 4 2 x 3 x 2 2 x 1 0,
☻ 5)6 x 4 5 x 3 38 x 2 5 x 6 0,
6)3 x 4 2 x 3 8 x 2 x 2 0,
7) x 4 2 x 3 9 x 2 6 x 9 0,
☻ 8) x 4 5 x 3 2 x 2 5 x 1 0.
а)Что у этих уравнений общего?
б)На какие две группы ты бы их разделил?
в)Если затрудняешься, сравни между собой коэффициенты каждого
уравнения.
6.
1) 24 x 4 16 x 3 3 x 2 0,4
3
2
2
)
x
5
x
6
x
5 x 1 0,
☻
3) x 4 11x 3 35 x 2 31x 6 0,
☻4) x 4 2 x 3 x 2 2 x 1 0,
☻5)6 x 4 5 x 3 38 x 2 5 x 6 0,
6)3 x 4 2 x 3 8 x 2 x 2 0,
7) x 4 2 x 3 9 x 2 6 x 9 0,
☻8) x 4 5 x 3 2 x 2 5 x 1 0.
г)Уравнения
такого
вида
называются
симметрическими.
д)Попробуй
записать
общий
вид
симметрического
уравнения
е)Сравни
свой результат
с уравнением:
Как
ты думаешь,
почему?
четвертой
степени.
Используй для обозначения
4
3
2
коэффициентов
буквы
a,b,c,
для переменной
ax bx cx аbx
a 0, х.
7. Решение симметрических уравнений.
x 5 x 6 x 5 x 1 0.4
3
2
8.
x 4 5 x 3 6 x 2 5 x 1 0.Имеем уравнение:
2
x 4 5x3 6 x 2 5x
1
y
2 5 y 6 0,
2 2 2 2 0, x 0 ?
2
x
x
x
x
x
2
y
5 y 4 0,
5
1
x 2 5 x 6 2 0,
y 1, y 4,
x x
5
2 1
1
1
x 2 5 x 6 0,
x 1 или x 4
x
x
x
x
2
2
1
2 1
x
1
x
x
4 x 1 0,
x 2 5 x 6 0.
x
x
x2 x 1 0
Пусть
x
2
1
1
y x y2
x
x
1
1
x2 2 x 2 y2 ,
x x
1
x2 2 2 y2 ,
x
1
2
x 2 y 2 2.
x
Ø
D1 4 1 3,
x 2
3
Ответ : 2
3
9. Реши симметрическое уравнение
x 2 x x 2 x 1 0, x 04
3
2
10.
Уравнение четвертой степени видаax bx cx bx a 0
4
3
2
является частным случаем уравнения
ax bx cx kbx k a 0
4
3
2
2
Оно называется возвратным уравнением.
11.
1) 24 x 4 16 x 3 3 x 2 0,2) x 4 5 x 3 6 x 2 5 x 1 0,
3) x 4 11x 3 35 x 2 31x 6 0,
4) x 4 2 x 3 x 2 2 x 1 0,
5)6 x 4 5 x 3 38 x 2 5 x 6 0,
6)3 x 4 2 x 3 8 x 2 x 2 0,
7) x 4 2 x 3 9 x 2 6 x 9 0,
8) x 5 x 2 x 5 x 1 0.
4
3
2
ax bx cx kbx k a 0
4
3
2
2
12.
VI.Решение возвратных уравнений.где k=3
x 4 2 x 3 9 x 2 6 x 9 0,
x 4 2 x 3 9 x 2 2 3 x 1 9 0,
6
9
2 0,
x
x
9
3
2
x 2 2 x 9 0,
x
x
3
3
9
9
2
2
2
x
t, x 2 x 2 t , x 2 t 2 6
x
x
x
x
x2 2x 9
t 2 6 2t 9 0, t 2 2t 15 0,
D1 1 15,
t 1 4, t1 3, t 2 5
3
3
x
5
x
3,
или
x
x
x 2 5 x 3 0,
x 2 3 x 3 0,
D 25 12 13,
D 9 12 0
x
5
13
2
Ø
Ответ :
5 13
2
13. Домашнее задание:
1) Доп. главы п.142) № 9.24 из сборника задач М.Л.Галицкого
3) В имеющейся у тебя математической литературе
поищи возвратные и симметрические уравнения и
реши наиболее интересные
4
3
2
x 5x 6 x 5x 1 0
4) Реши уравнение
двумя способами: способом группировки и как
симметрическое










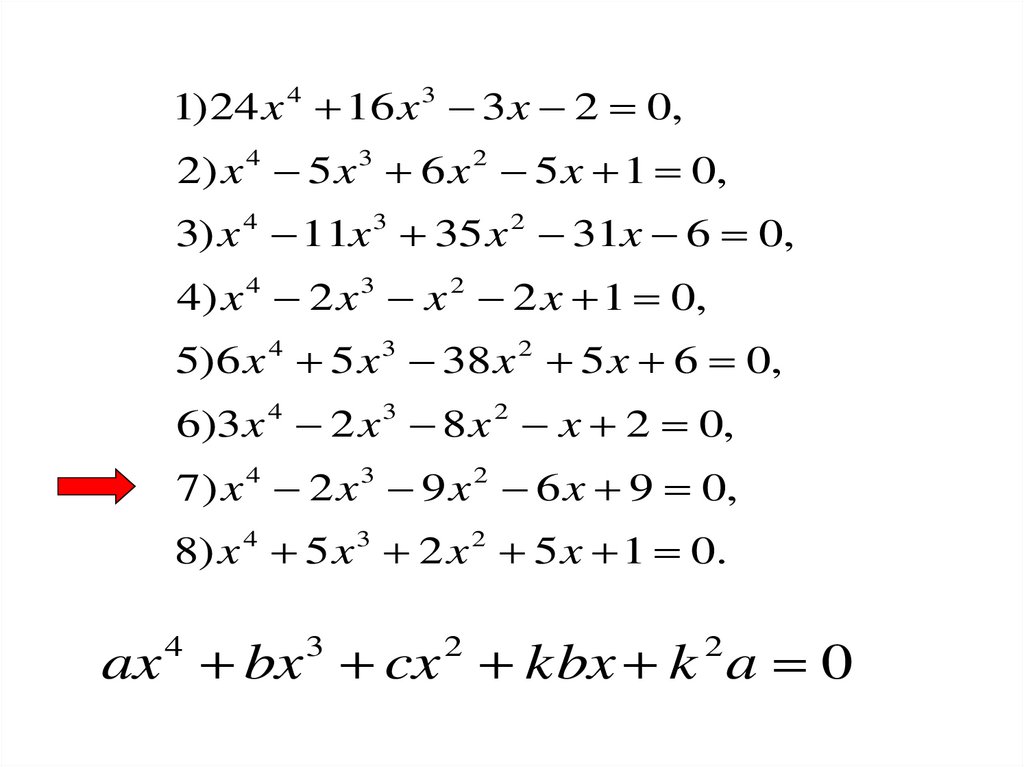


 Математика
Математика








