Многогранники, их виды. Элементы многогранника

1.

2.

- ввести понятие пространственного тела;
- рассмотреть виды пространственных тел;
- познакомиться с понятием многогранника;
- изучить элементы многогранника;
- рассмотреть правильные многогранники.

3.

Устный опрос
1. Какие два основных раздела геометрии изучаются в
школьном курсе?
2. Что изучается в планиметрии?
3. Такими фигурами являются….
4. Каким общим понятием можно назвать все эти фигуры?
5. Что такое многоугольник?
6. Какой многоугольник называется правильным?
7. Что изучает стереометрия?

4.

Фигуры в пространстве часто
называют пространственными
телами или телами.

5.

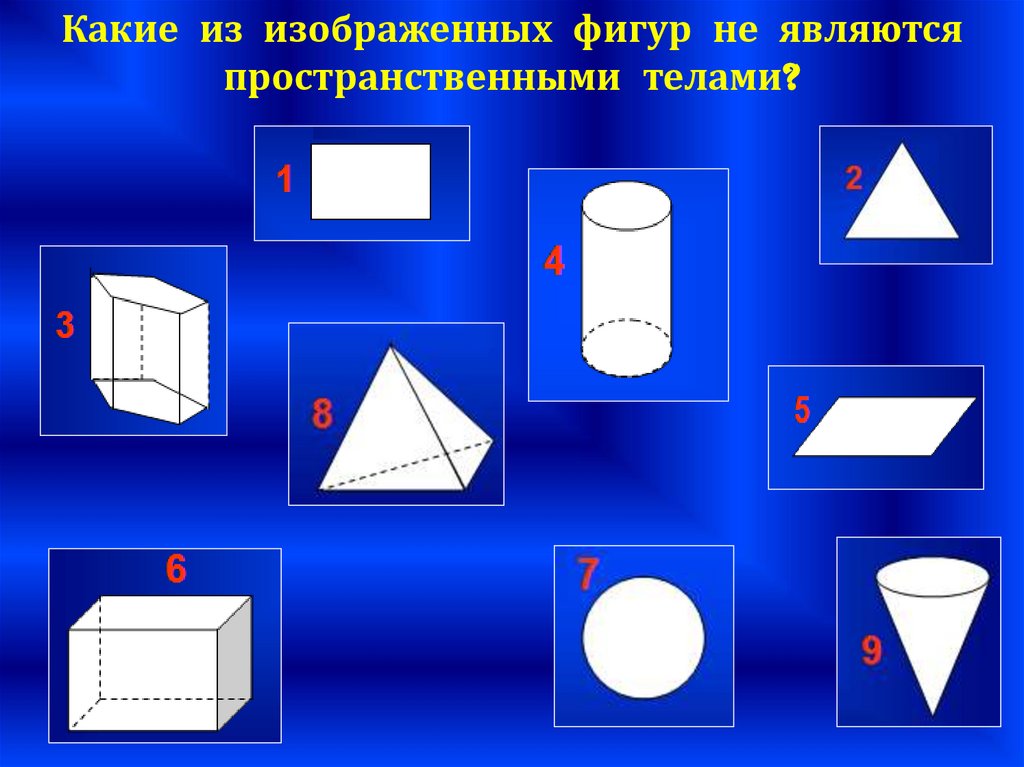
Какие из изображенных фигур не являются
пространственными телами?

6.

Пространственные тела
многогранники
тела
вращения

7.

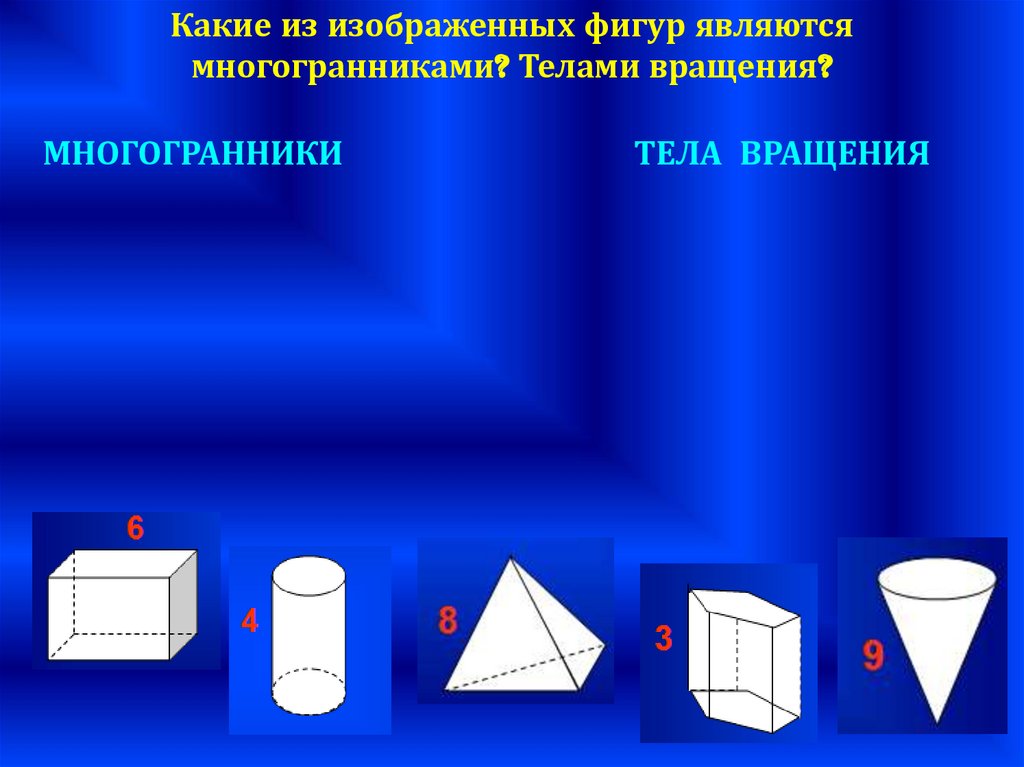
Какие из изображенных фигур являются
многогранниками? Телами вращения?
МНОГОГРАННИКИ
ТЕЛА ВРАЩЕНИЯ

8.

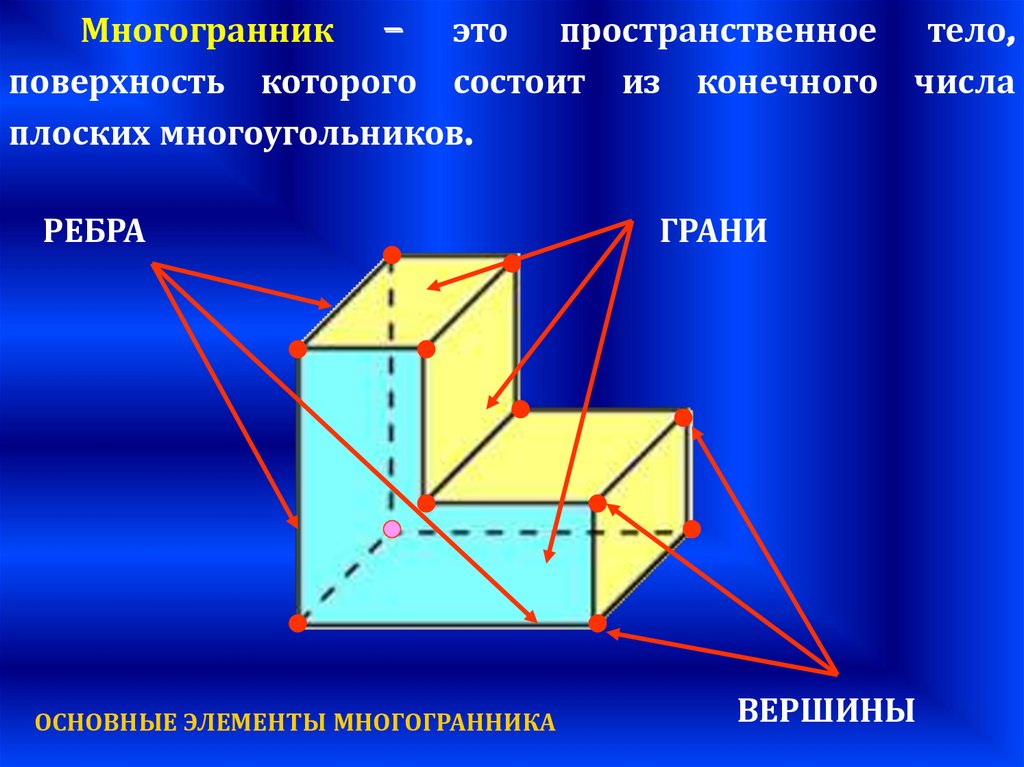
Многогранник – это пространственное тело,
поверхность которого состоит из конечного числа
плоских многоугольников.
РЕБРА
ОСНОВНЫЕ ЭЛЕМЕНТЫ МНОГОГРАННИКА
ГРАНИ
ВЕРШИНЫ

9.

• Грани многогранника - это
многоугольники, составляющие
поверхность многогранника.
• Ребра многогранника - это
стороны многоугольников.
• Вершины многогранника - это
вершины многоугольника.
• Диагональ многогранника - это
отрезок, соединяющий 2
вершины, не принадлежащие
одной грани.

10.

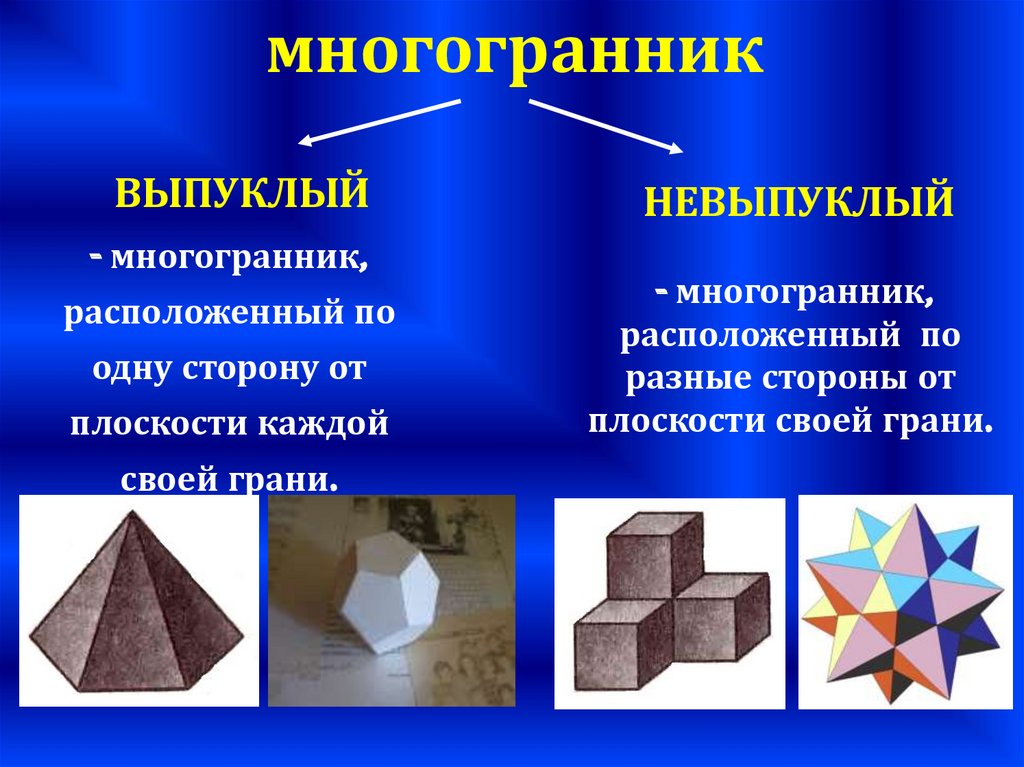
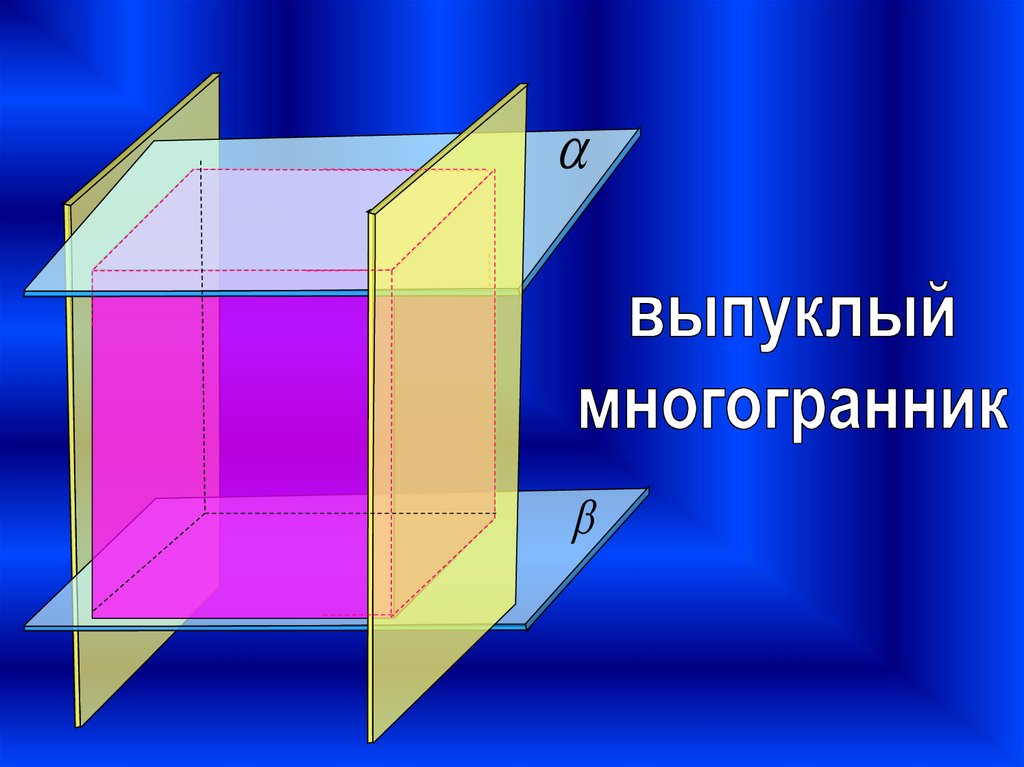
многогранник
ВЫПУКЛЫЙ
- многогранник,
расположенный по
одну сторону от
плоскости каждой
своей грани.
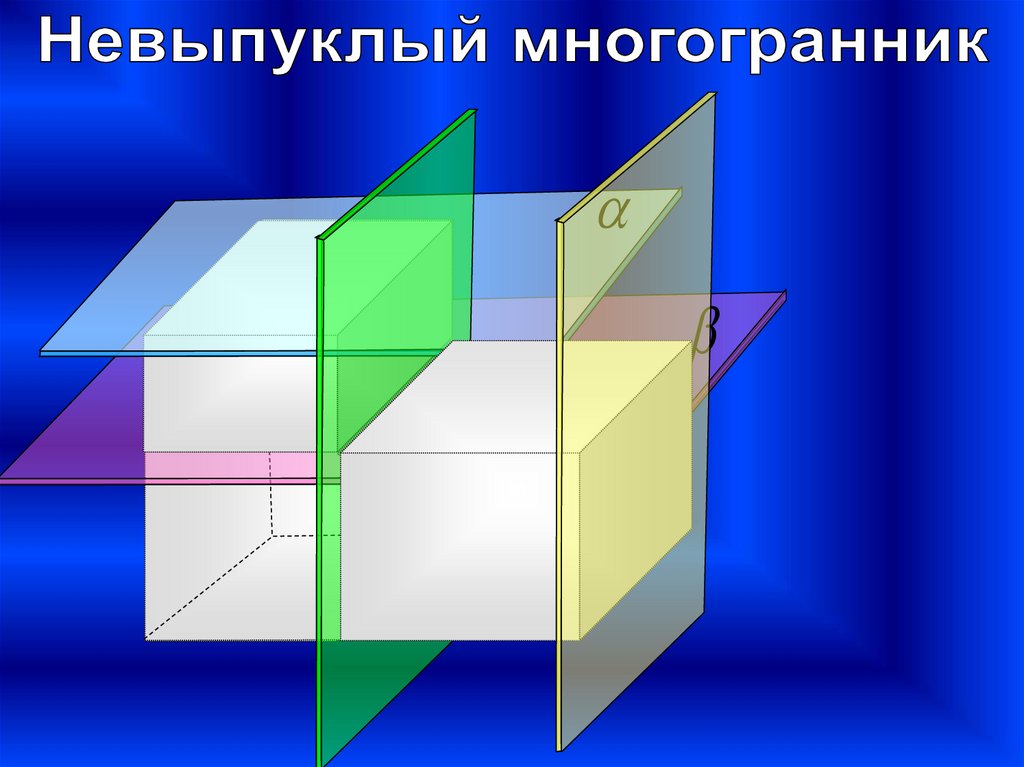
НЕВЫПУКЛЫЙ
- многогранник,
расположенный по
разные стороны от
плоскости своей грани.

11.

12.

13.

многогранник
ПРАВИЛЬНЫЙ
если все его грани - равные
между собой правильные
многоугольники и в каждой
вершине сходится одно и то же
число граней (или ребер)
Например, куб – все его грани – равные
квадраты, и к каждой вершине сходятся 3
ребра.
НЕПРАВИЛЬНЫЙ
если все его грани произвольные многоугольники и
в каждой вершине может
сходиться разное число граней.

14.

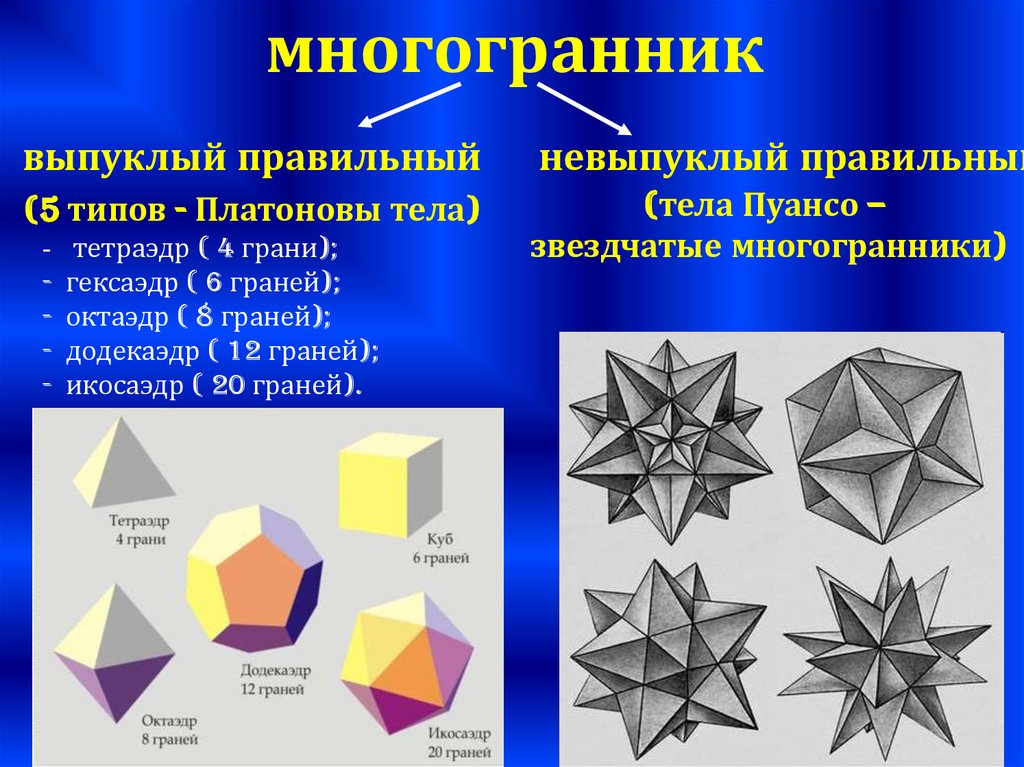
многогранник
выпуклый правильный
невыпуклый правильный
(5 типов - Платоновы тела)
(тела Пуансо –
звездчатые многогранники)
- тетраэдр ( 4 грани);
- гексаэдр ( 6 граней);
- октаэдр ( 8 граней);
- додекаэдр ( 12 граней);
- икосаэдр ( 20 граней).

15.

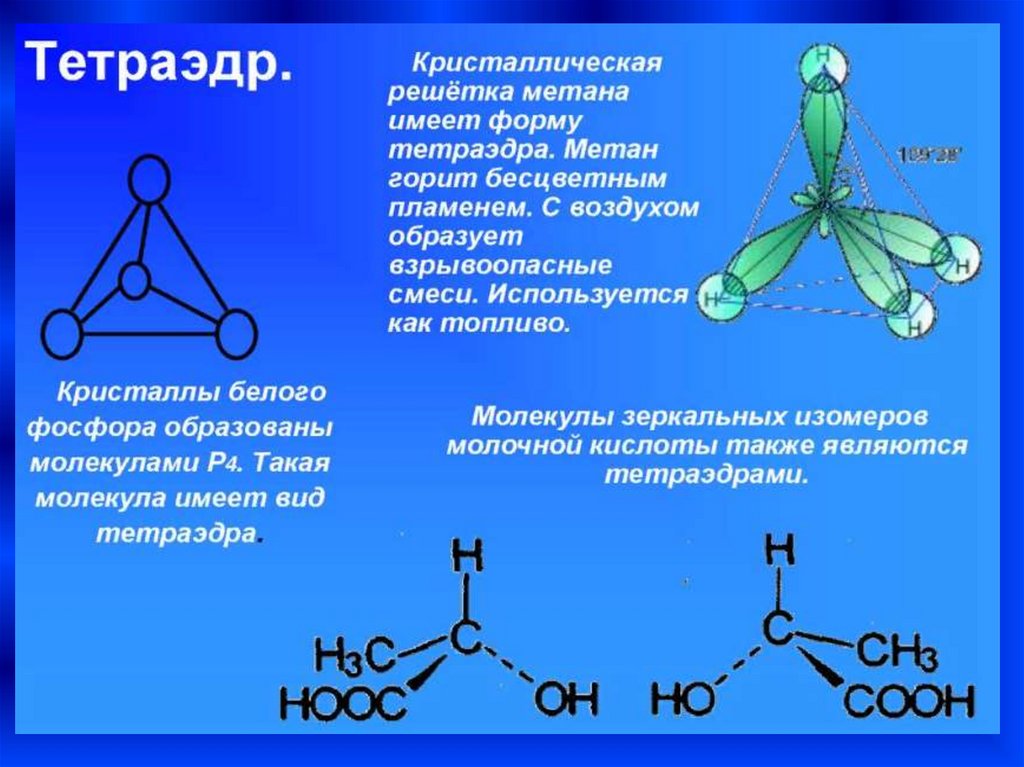
• Тетраэдр – это треугольная пирамида,
гранями которой являются треугольники.
• Тетраэдр - это правильный четырехгранник,
ограничен
четырьмя
равносторонними
треугольниками.
Каждая его вершина является вершиной трёх
треугольников. Следовательно, сумма плоских углов
при каждой вершине равна 180º.
В разных химических
реакциях применяется
сурьменистый
сернокислый натрий –
вещество,
синтезированное
учёными, кристалл
которого имеет форму
тетраэдра.
Молекулы воды имеют
форму тетраэдра.

16.

17.

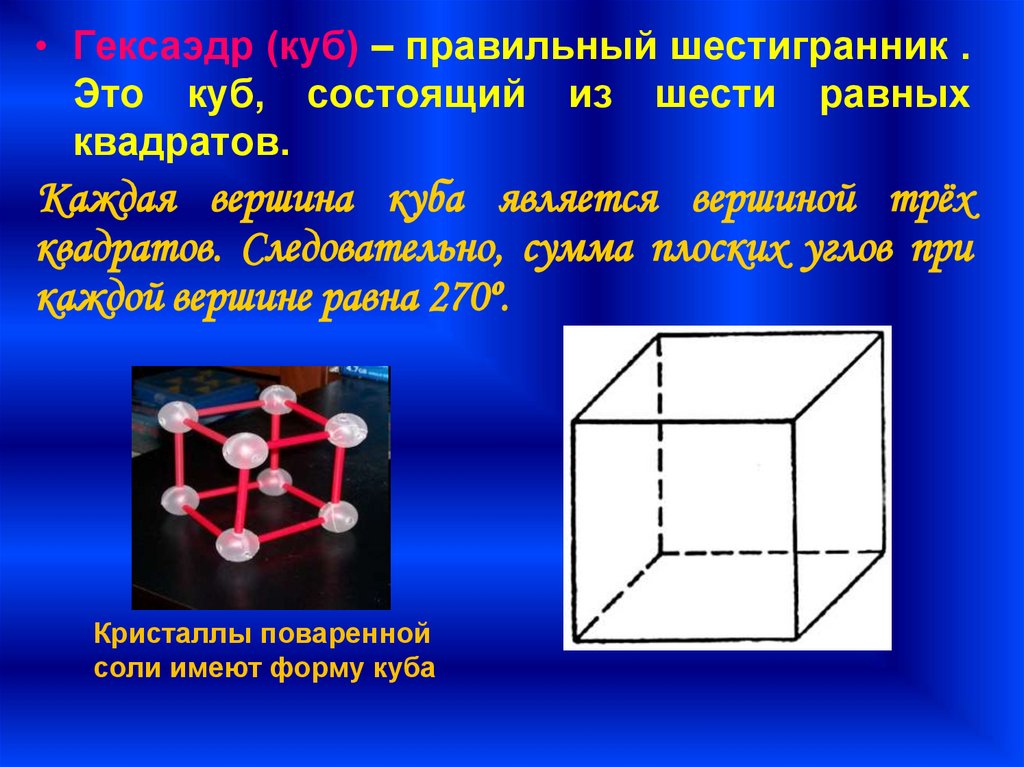
• Гексаэдр (куб) – правильный шестигранник .
Это куб, состоящий из шести равных
квадратов.
Каждая вершина куба является вершиной трёх
квадратов. Следовательно, сумма плоских углов при
каждой вершине равна 270º.
Кристаллы поваренной
соли имеют форму куба

18.

• Октаэдр – правильный восьмигранник,
состоящий из восьми равносторонних и
равных между собой треугольников.
• Каждая вершина октаэдра является вершиной четырёх
треугольников. Следовательно, сумма плоских углов при
каждой вершине 240º.
Правильная форма алмаза – октаэдр
При производстве алюминия пользуются алюминиево-калиевыми кварцами,
монокристалл которых имеет форму правильного октаэдра.
Минерал куприт образует кристаллы в форме октаэдров, пчелиные соты.

19.

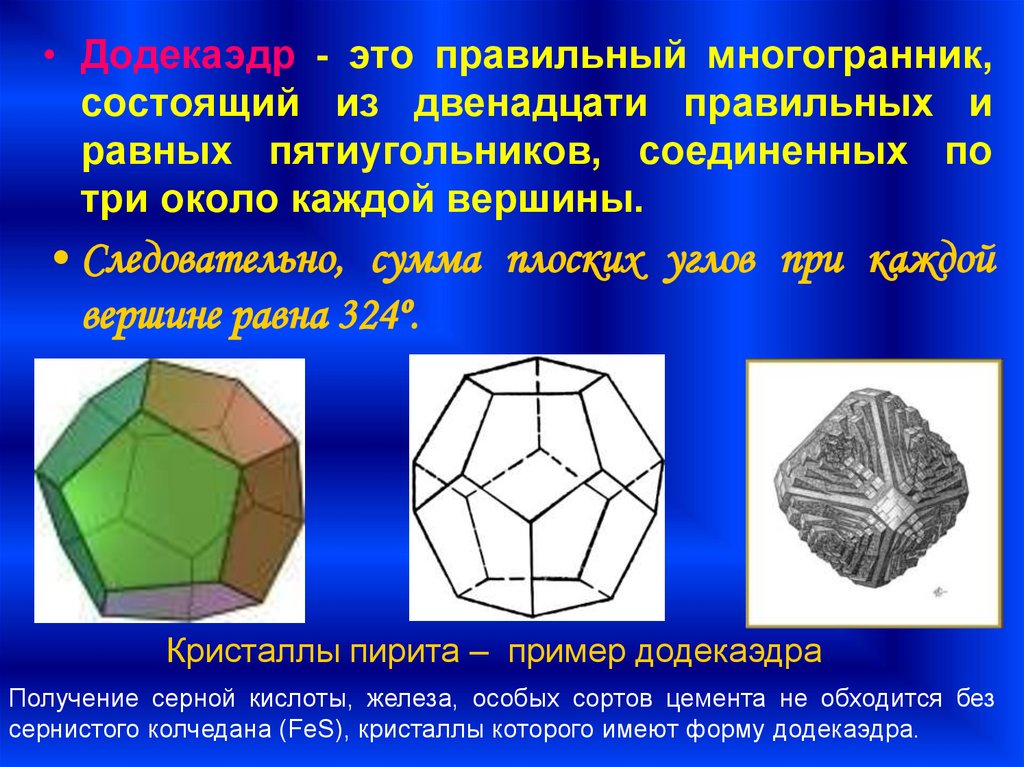
• Додекаэдр - это правильный многогранник,
состоящий из двенадцати правильных и
равных пятиугольников, соединенных по
три около каждой вершины.
• Следовательно, сумма плоских углов при каждой
вершине равна 324º.
Кристаллы пирита – пример додекаэдра
Получение серной кислоты, железа, особых сортов цемента не обходится без
сернистого колчедана (FeS), кристаллы которого имеют форму додекаэдра.

20.

• Икосаэдр – это многогранник, состоящий из 20
равносторонних
и
равных
треугольников,
соединенных по пять около каждой вершины.
Каждая вершина икосаэдра является вершиной
пяти треугольников. Следовательно, сумма
плоских углов при каждой вершине равна 300º.
Кристаллы бора имеют форму икосаэдра.
В своё время бор использовался для
создания полупроводников 1-го поколения.
Скелет одноклеточного организма
феодарии по форме напоминает
икосаэдр

21. Названия многогранников

пришли из Древней Греции,
в них указывается число граней:
«эдра» грань;
«тетра» 4;
«гекса» 6;
«окта» 8;
«икоса» 20;
«додека» 12.

22.

Правильные многогранники
в философской картине мира Платона
Правильные многогранники иногда называют Платоновыми
телами, поскольку они занимают видное место в философской картине
мира, разработанной великим мыслителем Древней Греции Платоном
(ок. 428 – ок. 348 до н.э.).
Платон считал, что мир строится из четырёх «стихий» – огня, земли,
воздуха и воды, а атомы этих «стихий» имеют форму четырёх
правильных многогранников.
Тетраэдр олицетворял огонь, поскольку его вершина устремлена
вверх, как у разгоревшегося пламени.
Икосаэдр – как самый обтекаемый – воду.
Куб – самая устойчивая из фигур – землю.
Октаэдр – воздух.
В наше время эту систему можно сравнить с четырьмя состояниями
вещества – твёрдым, жидким, газообразным и пламенным.
Пятый многогранник – додекаэдр символизировал весь мир и
почитался главнейшим.
Это была одна из первых попыток ввести в науку идею
систематизации.

23.

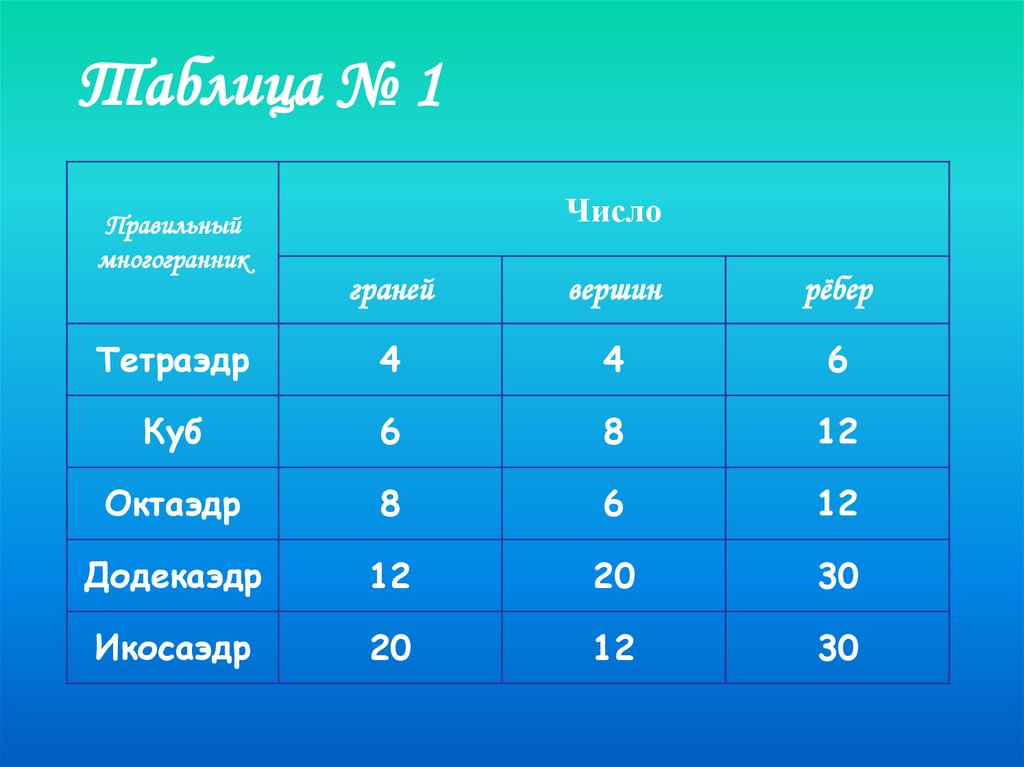
Таблица № 1
Правильный
многогранник
Число
граней
вершин
рёбер
Тетраэдр
4
4
6
Куб
6
8
12
Октаэдр
8
6
12
Додекаэдр
12
20
30
Икосаэдр
20
12
30

24.

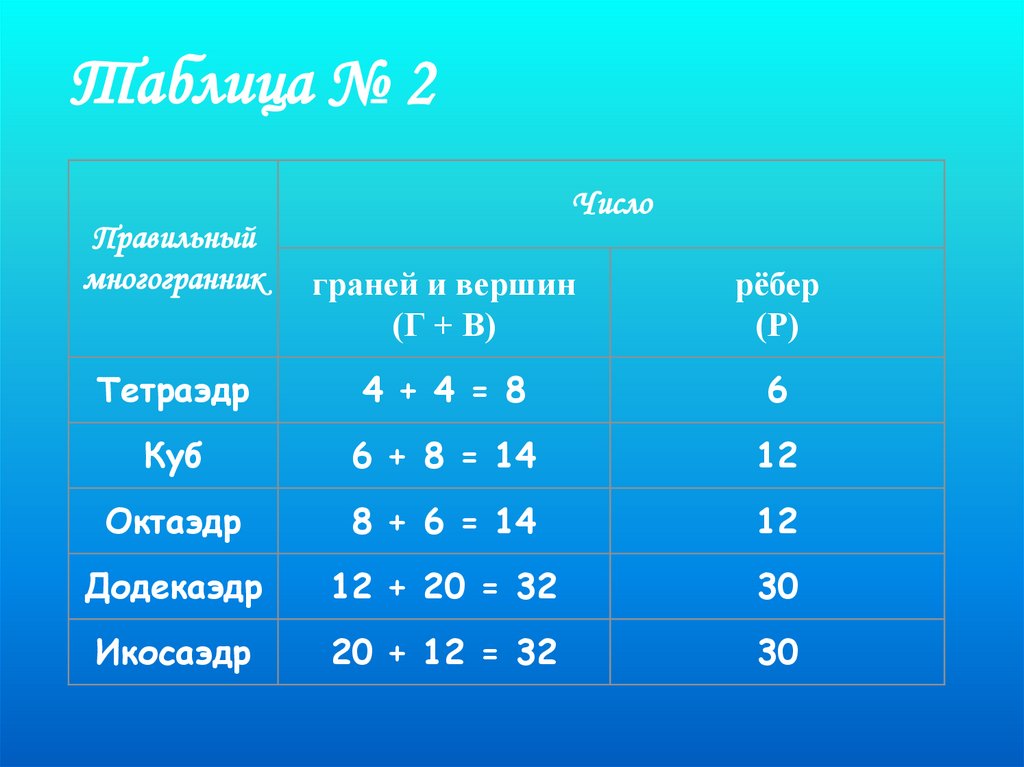
Таблица № 2
Правильный
многогранник
Число
граней и вершин
(Г + В)
рёбер
(Р)
Тетраэдр
4 + 4 = 8
6
Куб
6 + 8 = 14
12
Октаэдр
8 + 6 = 14
12
Додекаэдр
12 + 20 = 32
30
Икосаэдр
20 + 12 = 32
30

25.

Для
любого
выпуклого
многогранника
справедлива формула Эйлера, устанавливающая
связь между числом вершин, граней и ребер
многогранника.
Теорема Эйлера
Для любого выпуклого многогранника
число граней плюс число вершин минус
число рёбер равно 2.
Г+В-Р=2

26.

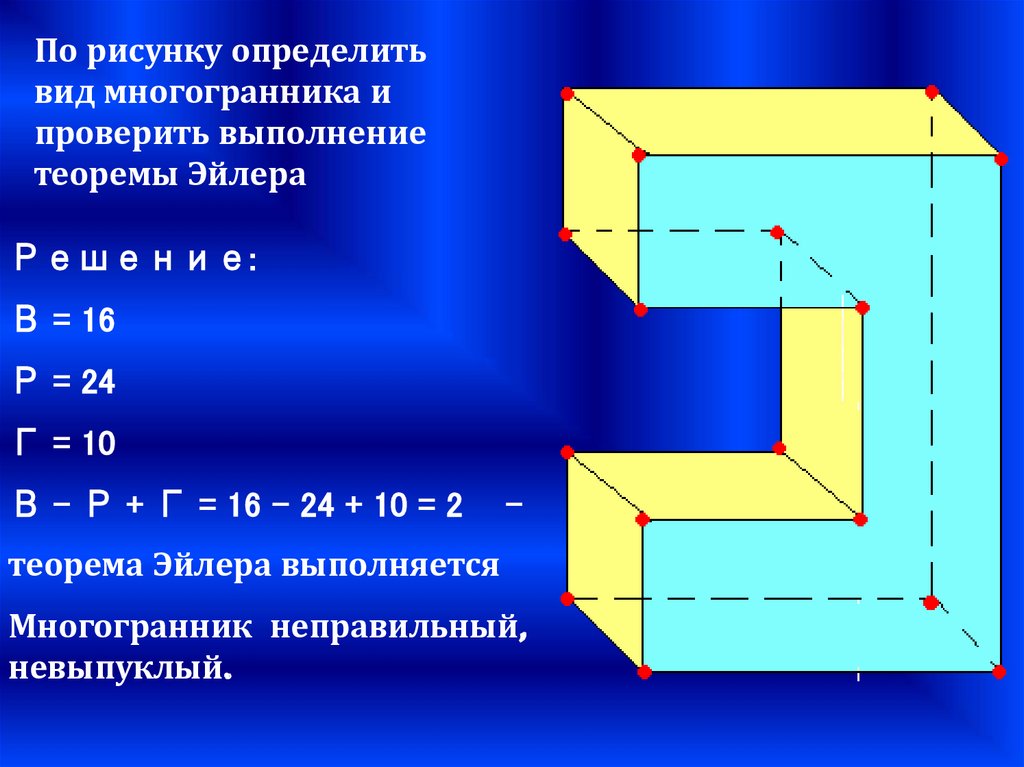
По рисунку определить
вид многогранника и
проверить выполнение
теоремы Эйлера
Решение:
В = 16
Р = 24
Г = 10
В – Р + Г = 16 – 24 + 10 = 2
-
теорема Эйлера выполняется
Многогранник неправильный,
невыпуклый.

27.

ПРИМЕНЕНИЕ МНОГОГРАННИКОВ
Самый большой правильный
многогранник в мире – пирамида
Хеопса!
Башни Азриэли – торговый центр в
Тель-Авиве (Израиль).
Комплекс из трех башен –
квадратной, круглой и треугольной
(трехгранной призмы, цилиндра,
параллелепипеда)

28.

Футбольный мяч представляет собой
модель многогранника с 32 гранями, 20 из
которых – правильные шестиугольники
(белые), а 12 – правильные пятиугольники
(чёрные). Такие многогранники называются
полуправильными.
Спасская башня Кремля - четыре яруса башни
представляют из себя куб, многогранники и
пирамиду.

29.

1. выучить теорию;
2. написать 5 примеров применения многогранников в
жизни;
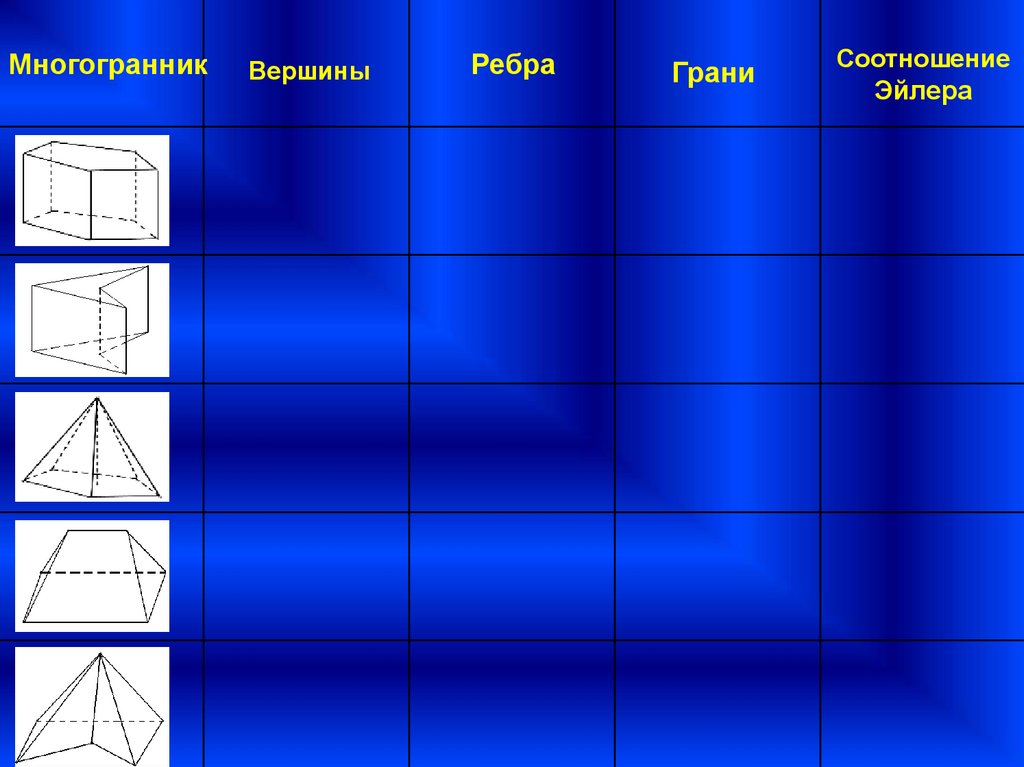
3. заполнить таблицу.

30.

Многогранник
Вершины
Ребра
Грани
Соотношение
Эйлера