Похожие презентации:
Системы линейных алгебраических уравнений
1. Системы линейных алгебраических уравнений
2.
Общий вид системы линейных алгебраических уравнений (СЛАУ).3.
Решение системы линейных алгебраических уравненийРассмотрим некоторый набор значений переменных xi, xi= i.
4.
Матричная форма записи системы линейных алгебраическихуравнений.
5.
Элементарные преобразования системы линейныхалгебраических уравнений.
Элементарным преобразованиям строк расширенной матрицы А|B
СЛАУ соответствуют преобразования уравнений.
Исходная система и система, полученная из нее с помощью
элементарных преобразований, имеют одно и то же решение.
6.
СЛАУ равносильны при следующих преобразованиях:7.
Решение системы уравнений AX=B (основной случай)Пусть имеется СЛАУ с квадратной матрицей A, причем определитель
этой матрицы отличен от 0.
Метод обратной матрицы
состоит в вычислении решения по формуле
Метод с использованием расширенной матрицы
8.
Решение системы уравнений AX=B (основной случай)Метод с использованием формул Крамера.
9.
Решение СЛАУ общего вида методом Гаусса.10.
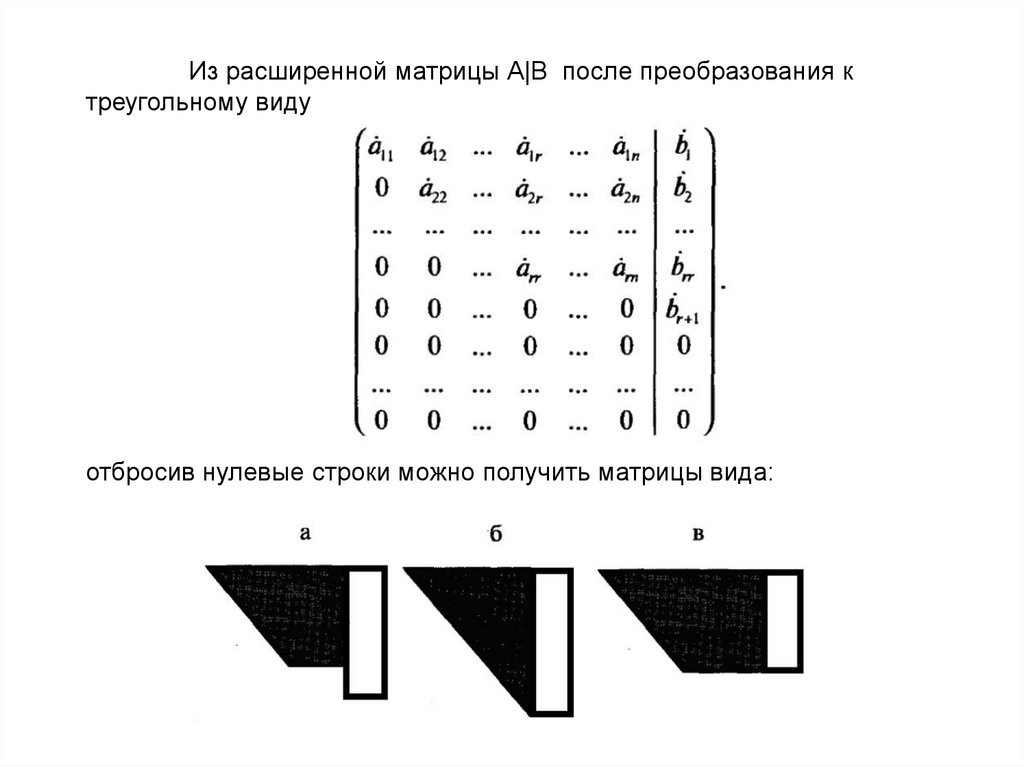
Из расширенной матрицы А|B после преобразования ктреугольному виду
отбросив нулевые строки можно получить матрицы вида:
11.
Система линейных алгебраических уравнений может не иметьрешения
12.
Система линейных алгебраических уравнений может иметьединственное решение.
13.
Система линейных алгебраических уравненийможет иметь бесконечно много решений.
14.
Ответ на вопрос о существовании решений СЛАУ можнополучить также с помощью теоремы Кронекера-Капелли.
Ранг матрицы равен числу линейно-независимых строк (столбцов)
Ранг матрицы можно определить, приведя ее к ступенчатому виду с
помощью элементарных преобразований.
Если в расширенной матрице СЛАУ A|B есть линейно-зависимая
строка, с помощью элементарных преобразований можно получить
матрицу (а значит, равносильную СЛАУ), где соответствующая
строка будет состоять целиком из нулей.
Если в матрице A есть линейно-зависимая строка, можно
преобразовать эту матрицу так, чтобы строка с соответствующим
номером обратилась в нулевую.
15.
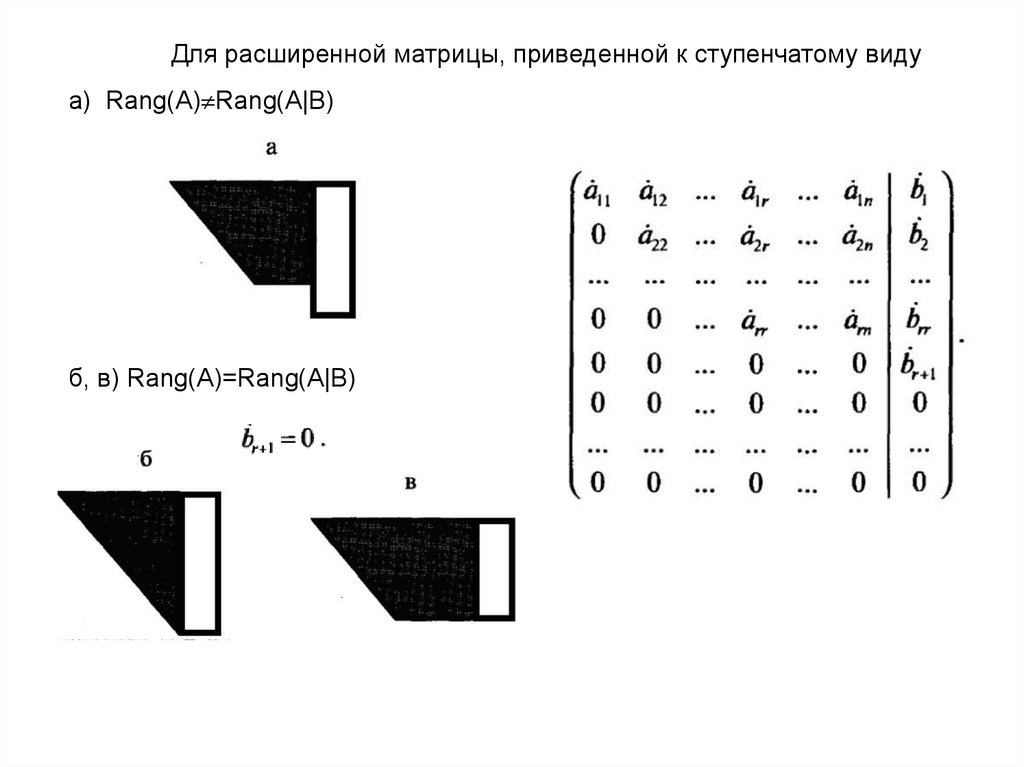
Для расширенной матрицы, приведенной к ступенчатому видуа) Rang(A) Rang(A|B)
б, в) Rang(A)=Rang(A|B)
16.
Совместность СЛАУ и число линейно-независимых уравнений.Число уравнений m в системе может быть больше, меньше или
равно числу переменных n, но с помощью элементарных преобразований из
системы можно исключить все линейно-зависимые уравнения и получить
равносильную систему, в которой число уравнений равно рангу r исходной
расширенной матрицы.
В случае а) система несовместна Rang(A) Rang(A|B)=r
В случае б) совместна, число линейно-независимых уравнений
r=Rang(A)=Rang(A|B)=n
В случае б) совместна, число линейно-независимых уравнений
r=Rang(A)=Rang(A|B) n
17.
Однородные системы линейных алгебраических уравнений.18.
Свойства однородной системы уравнений.19.
.20.
Фундаментальная система решений.21.
Построение общего решения однородной СЛАУ (r<n).22.
.Величины xij - коэффициенты, полученные при
преобразованиях элементов aij матрицы А, позволяющих
выразить базисные переменные xi через свободные
23.
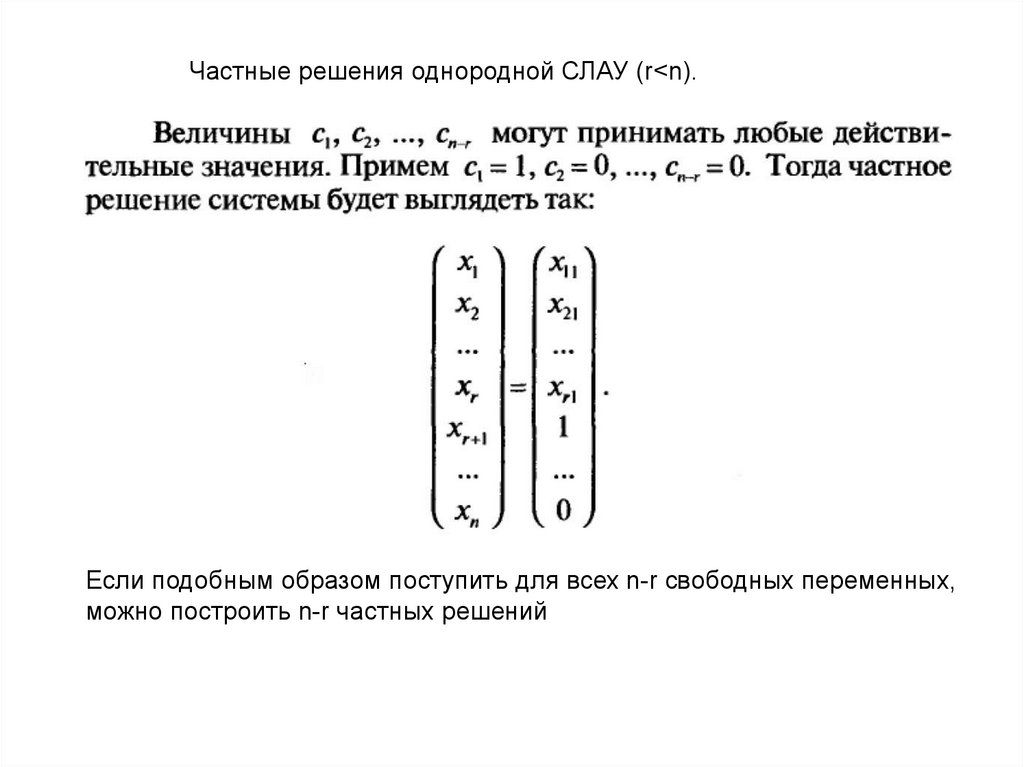
Частные решения однородной СЛАУ (r<n).Если подобным образом поступить для всех n-r свободных переменных,
можно построить n-r частных решений
24.
Матрица частных решений СЛАУ (r<n). .25.
Общее решение однородной СЛАУ (r<n). .26.
Общее решение неоднородной системы линейныхалгебраических уравнений.
Неоднородная СЛАУ - это СЛАУ с B 0.
27.
Далее, расширенную матрицу приведем к ступенчатому виду, и выразимбазисные переменные через свободные




























 Математика
Математика








