СЛАУ

1. Теорема Кро́некера — Капе́лли

Системы линейных
алгебраических уравнений.
Теорема
Кро́некера — Капе́лли

2. Леопольд Кронекер немецкий математик

07.12.1823 — 29.12.1891
Родился 7 декабря 1823, Лигниц,
Германия, ныне Легница, Польша в
еврейской семье, за год до смерти
принял христианство.
Иностранный корреспондент
Петербургской Академии наук
(1872), член Берлинской АН (1861),
профессор университета в Берлине.
Основные труды по алгебре и
теории чисел.
Большое значение имеют его
исследования по арифметической
теории алгебраических величин.

3. Альфред Капелли итальянский математик

Родился 5 августа 1855 года в Милане. В
1877 году окончил Римский
университет.
В 1881 году стал профессором
алгебраического анализа в университете
Палермо. В 1886 году переехал в
Неаполь и остался жить в этом городе до
самой смерти. В Неапольском
университете возглавил кафедру
алгебры. С 1894 по 1910 годы,
продолжая профессорскую
деятельность, был редактором
математического издания членом
Национальной академии.
05.08.1855 — 28.01.1910

4.

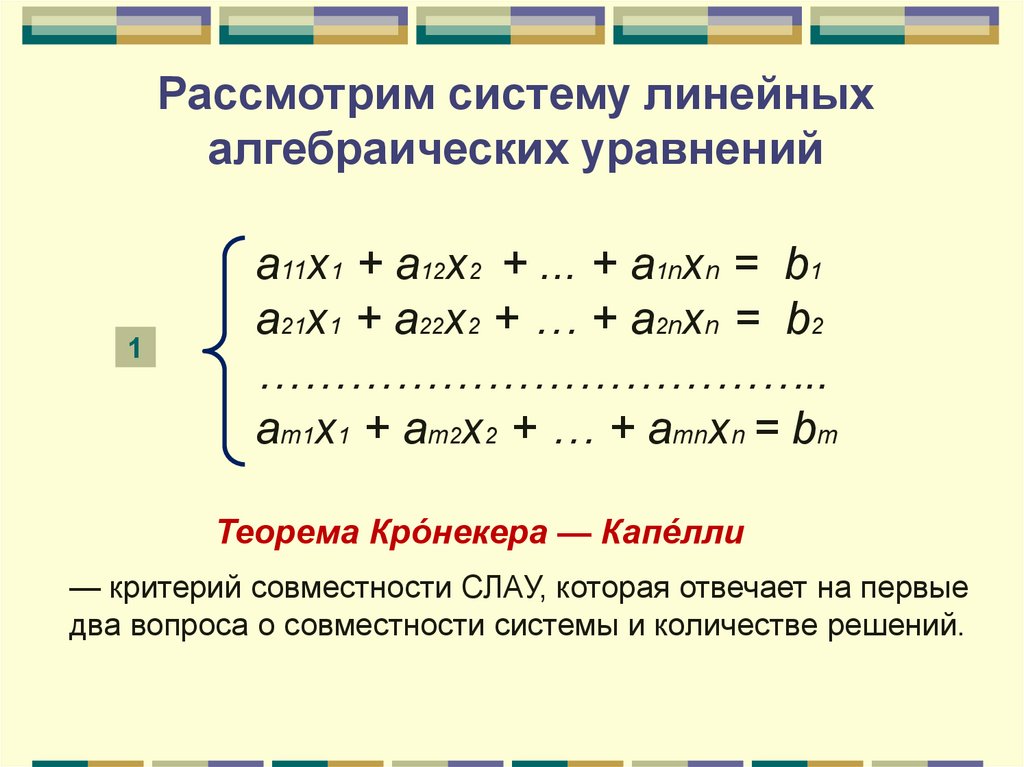
Рассмотрим систему линейных
алгебраических уравнений
1
а11x1 + а12x2 + ... + а1nxn = b1
a21x1 + a22x2 + … + a2nxn = b2
………………………………..
am1x1 + am2x2 + … + amnxn = bm
Теорема Кро́некера — Капе́лли
— критерий совместности СЛАУ, которая отвечает на первые
два вопроса о совместности системы и количестве решений.

5.

Вспомним такие понятия как:
А=
а11 а12 ... ..a1n
a21 a22 … ..a2n
........................
am1 am2 … amn
A/B =
а11 а12 ... a1n
b1
a21 a22 … a2n
b2
.....................
....
am1 am2 … amn bm
А – основная матрица системы
В – матрица-столбец свободных членов.
А|В - расширенная матрица системы
СЛАУ ( 1 )
B=
b1
b2
….
bm

6. Теорема Кро́некера — Капе́лли

Теорема Кро́некера — Капе́лли
Для того, чтобы система линейных уравнений (1)
была совместной, необходимо и достаточно, чтобы
ранг расширенной матрицы этой системы был равен
рангу ее основной матрицы
rang A/B = rang A
система совместна.
система имеет
единственное
решение.
система имеет
бесконечно
много решений.
rang (A/B)= rang (A)= n
rang (A/B) = rang (A)< n
Где n число неизвестных переменных в заданной СЛАУ
rang (A) ≠ rang (A/B)
система несовместна.

7. Следствие из теоремы Кронекера-Капелли

Следствие из теоремы КронекераКапелли
Если rangA ≠ rangÃ, то СЛАУ
несовместна (не имеет решений).
Если rangA = rang à < n, то СЛАУ
является неопределённой (имеет
бесконечное количество решений).
Если rangA = rang à = n, то СЛАУ
является определённой (имеет ровно
одно решение).

8. Рассмотрим пример 1

Задание.
Задана система уравнений. Вычислим ранги основной и
расширенной матрицы, т.е. проверим систему на
совместимость.
Х1 + Х2 = 3
Х1 – Х2 = 1
Решение.
1 1
А = 1 -1
A|B=
- основная матрица.
1 1
1 -1
3
1
- расширенная матрица.

9.

1) Найдём ранг основной матрицы А
1
Μ2 =
1 1
1 -1
= (-1-1)= -2
Старший минор не равен нулю
rang (A) = 2
2) Найдём ранг расширенной матрицы АΙΒ
1
Μ2 =
1
-1
3 = (1+3)= 4
1
Старший минор не равен нулю
rang (AΙΒ) = 2
Получаем: rang(A) = rang(A|B)=2, количество переменных в системе
n=2, то по теореме Кронекера - Капелли система имеет решение, и
только одно.
Ответ: Система является - совместной определённой

10. Рассмотрим пример 2

Задание.
Задана система уравнений. Вычислим ранги основной и
расширенной матрицы, т.е. проверим систему на
совместимость.
Х1 + Х2 = 3
2Х1 + 2Х2 = 6
Решение.
1
А= 2
1
2
- основная матрица.
A|B=
1
2
1
2
3
6
- расширенная матрица.

11.

1) Найдём ранг основной матрицы А
1
Μ1 = Ι2Ι =2
rang (A) = 1
2) Найдём ранг расширенной матрицы АΙΒ
1
Μ1 = Ι2Ι = 2
rang (AΙΒ) = 1
Получилось, что rang(A) = rang(A|B)= 1, но n=2. (1<2)
Следовательно, система совместна, имеет бесконечное
множество решений.
Ответ: Система является - совместной неопределённой

12. Рассмотрим пример 3

Задание.
Задана система уравнений. Вычислим ранги основной и
расширенной матрицы, т.е. проверим систему на
совместимость.
Х1 + Х2 = 3
Х1 + Х2 = 7
Решение.
1
А= 1
1
1
- основная матрица.
A|B=
1
1
1
1
3
7
- расширенная матрица.

13.

1) Найдём ранг основной матрицы А
1
Μ1 = Ι1Ι =1
rang (A) = 1
2) Найдём ранг расширенной матрицы АΙΒ
1
Μ2 =
1
1
3 = (7-3)= 4
7
Старший минор не равен нулю
rang (AΙΒ) = 2
Итак, rang(A) = 1, rang(A|B) = 2, они не равны,
следовательно, система не имеет решений.
Ответ: Система является - несовместной

14. Рассмотрим пример 4

Задание.
Рассмотрим пример 4
Задана система уравнений. Вычислим ранги основной и
расширенной матрицы, т.е. проверим систему на
совместимость.
2
Решение.
2
Х1 + Х2 = 25
Х1 - Х2 = 0
Эту систему не исследуем, так как теорема
Кронекера - Капелли применима только к
системам линейных алгебраических
уравнений.

15. Рассмотрим пример 5

Задание.
Задана система уравнений. Вычислим ранги основной и
расширенной матрицы, т.е. проверим систему на
совместимость.
Х1 + 2Х2 = 0
3Х1 + 5Х2 = 0
Решение.
1
А= 3
2
5
- основная матрица.
A|B=
1
3
2
5
0
0
- расширенная матрица.

16.

1) Найдём ранг основной матрицы А
1
Μ2 =
1 2 = (5-6)= -1
rang (A) = 2
3 5
2) Найдём ранг расширенной матрицы АΙΒ
1
Μ2 =
1
3
2 = (5-6)= -1
5
Количество переменных n=2.
rang (AΙΒ) = 2
rang(A) = rang(A|B) = 2
Ответ: система является совместимой и имеет единственное
решение. А так как система однородная, то это единственное
решение и есть (0;0).
ПРИМЕЧАНИЕ
В однородных системах ранги основной матрицы и
расширенной всегда равны между собой. Столбец свободных
членов в расширенной матрице – нулевой.

17. Рассмотрим пример 6

Задание.
Задана система уравнений. Вычислим ранги основной и
расширенной матрицы, т.е. проверим систему на
совместимость.
2Х1 + 3Х2 = 0
6Х1 + 9Х2 = 0
Решение.
2
А= 6
3
9
- основная матрица.
A|B=
2
6
3
9
0
0
- расширенная матрица.

18.

1) Найдём ранг основной матрицы А
2
А= 6
3
9
2
0
⇔
3
0
rang (A) = 1
2) Найдём ранг расширенной матрицы АΙΒ
A|B=
2
6
3
9
0
0
⇔
2
0
3
0
0
0
rang (АΙΒ) = 1
Итак: rang(A) = rang(A|B) = 1
Количество переменных n=2.
Значит, система имеет бесконечное множество решений
Ответ: Система является - совместной неопределённой

19.

Рассмотрим пример 7
Задание.
Задана система уравнений. Вычислим ранги основной и
расширенной матрицы, т.е. проверим систему на
совместимость.
3x + 4y + 7z = 0
x - 5y + 6z = 1
Решение.
8x + y – z = 10
3 4 7
А = 1 -5 6
8 1 -1
A|B=
- основная матрица.
3 4 7
1 -5 6
8 1 -1
0
1 - расширенная матрица.
10

20.

1) Найдём ранг основной матрицы А
1
Μ3 =
3 4 7
1 -5 6
8 1 -1
= 15+7+192 +280-18+4 = 480
Старший минор не равен нулю
rang (A) = 3
2) Найдём ранг расширенной матрицы АΙΒ
1
Μ3 =
3 4 7
1 -5 6
8 1 -1
Старший минор не равен нулю
= 480
rang (АΙΒ) = 3
Ответ: Это неоднородная система трех линейных уравнений с
тремя неизвестными. Система является - совместной определённой
- (решение только одно).

21.

Если rangA = rang à = n, то свободных
неизвестных нет.
В этом случае СЛAУ имеет
единственное решение (определённая
СЛAУ).
• Если rangA = rang à < n, то СЛAУ
неопределённая. В этом случае
находят общее решение СЛAУ.

22.

•Решение СЛAУ, в котором базисные неизвестные
выражены через свободные неизвестные,
называется общим решением СЛAУ.
•Решение, которое получается из общего путём
присваивания свободным неизвестным числовых
значений, называется частным решением СЛAУ.
Для нахождения общего решения СЛАУ нужно
1. выбрать базисный минор (обычно это минор, под
главной диагональю которого – все нули);
2. перенести свободные неизвестные к свободным
членам, то есть в правые части уравнений;
3. обратным ходом метода Гаусса выразить
базисные неизвестные через свободные
неизвестные.

23.

Фундаментальной системой
частных решений системы n
однородных линейных уравнений
(СОЛУ) называется система линейно
независимых частных решений, число
решений в которой равно числу k = n – r
свободных неизвестных системы,
где r - ранг основной матрицы системы.

24.

Фундаментальную систему частных решений
(ФСЧР СОЛУ) получают обычно,
последовательно приравнивая свободные
неизвестные элементам строк единичной
матрицы порядка k = n – r
Замечание. ФСЧР СОЛУ можно получить также,
приравнивая свободные неизвестные
элементам строк произвольной квадратной
матрицы А порядка, если Δ≠0

25.

Метод Крамера
1. Находим определитель системы Δ.
2. Вычисляем определители Δх1, Δ x2, …
3. Возможны три случая:
а) Если Δ ≠0, то система имеет единств.
решение:
б) Если Δ =0, но хотя бы один из
определителей Δ хi не равен нулю, то
система не имеет решений.
в) Если Δ =0, Δ х1=0, Δ х2=0, …, Δ хn=0, то
система имеет бесконечное множество
решений.