Похожие презентации:
Статистическая радиофизика. Модели случайных процессов. (Тема 4)
1. Статистическая радиофизика
Тема 4Модели случайных процессов
1
2. Общий план курса
1.2.
3.
4.
5.
6.
Случайные процессы и методы их описания.
Модели случайных процессов.
Шумовые колебания в линейных системах.
Шумовые колебания в нелинейных системах.
Фильтры.
Основы теории передачи информации по каналам
связи
2
3. Модели случайных процессов (план) см [1]. Глава 2
Спектральный анализ сигналов
Гауссовский случайный процесс
Узкополосный стационарный шум
Узкополосный гауссовский шум
Узкополосный негауссовский шум
Диффузионный (винеровский) процесс
Колебания, модулированные шумом
- амплитудная модуляция
- фазовая модуляция
- частотная модуляция
• Импульсные случайные процессы
3
4. Спектральный анализ сигналов
1) Периодические сигналы2p
2p
F (t ) = F (t + nT ); T =
; =
.
T
Где - круговая частота, n - любое
положительное целое число
n
F (t ) = a0 + å ( ak cos( k t ) +bk sin( k t ))
k =1
4
5.
Коэффициенты разложения ряда Фурье2p
1
a0 =
2p
ò F ( t )d t;
0
1
ak =
p
2p
1
bk =
p
2p
ò F ( t ) cos(k t )d t;
0
ò F ( t ) sin(k t )d t.
0
5
6. Формы представления ряда Фурье
ak cos( k t ) + bk sin( k t ) = Ck cos(k t - j k )Ck = a k
2
æ bk ö
+ bk , j k = arctg ç ÷
è ak ø
2
1 i t
1 i t
- i t
cos t = ( e + e ) ; sin t = ( e - e - i t )
2
2i
1
ak cos(k t ) + bk sin( k t ) = éë ak ( e i t + e - i t ) - ibk ( e i t - e - i t ) ùû =
2
1
= éë ( ak - ibk ) ei t + ( ak + ibk ) e - i t ùû .
2
6
7. Формы представления ряда Фурье
nF (t ) = a0 + å Ck cos( k t - j k )
k =1
n
1
F (t ) = å éë( ak - ibk ) exp(ik t ) + ( ak + ibk ) exp( -ik t ) ùû =
k =0 2
n
= å [ ck exp(ik t ) + c- k exp( -ik t ) ] =
k =0
=
n
åc
k =- n
k
exp(ik t ).
1
1
ck = ( ak - ibk ) . c- k = ck * = ( ak + ibЗдесь
k
³0
k).
2
2
T
1
ck = ò F (t ) exp( -ik t )dtЗдесь
.
n ³
k ³ n- n
, ³ 0.
T 0
7
8.
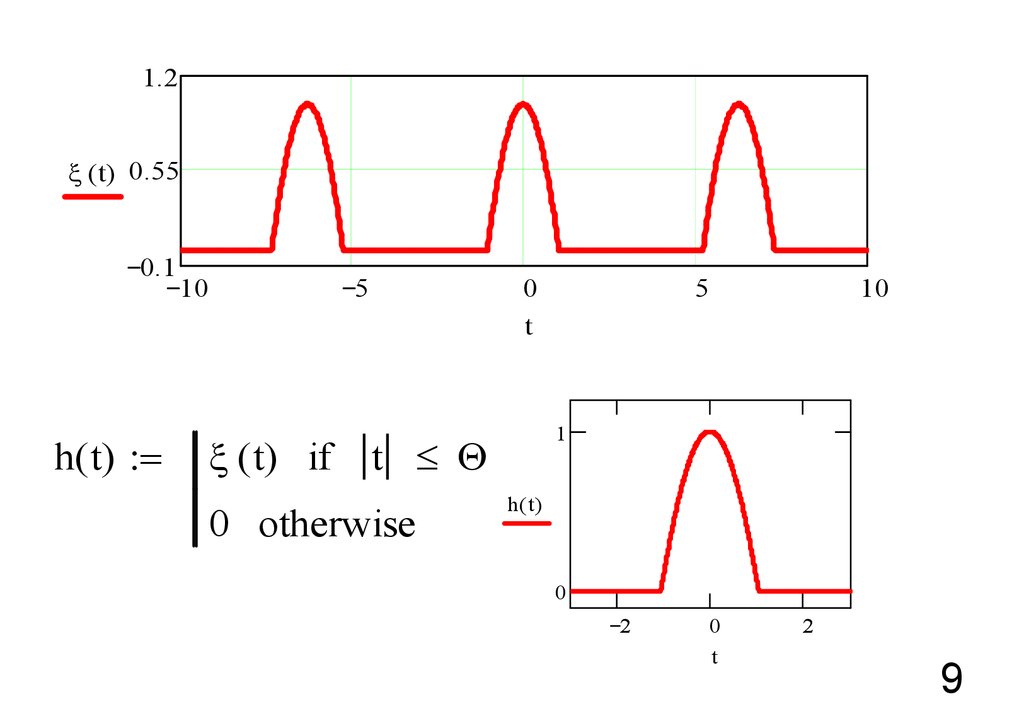
Пример 1. Периодическая последовательностькосинусоидальных импульсов.
Угол отсечки = 60 deg. Период Т=2p
= 60 deg
= 1.047
AM = 1
æ cos ( t) - cos ( ) ö
( t) = AM maxç
0÷
è 1 - cos ( )
ø
8
9.
1.2( t) 0.55
0.1
h( t) =
10
5
( t) if
0
t
10
1
t
0 otherwise
5
h ( t)
0
2
0
t
2
9
10.
k = 0 10p
2
ak =
h( t) cos ( k t) dt
p 0
p
2
a0 =
h( t) dt
p 0
p
2
bk =
h( t) sin( k t) dt
p 0
10
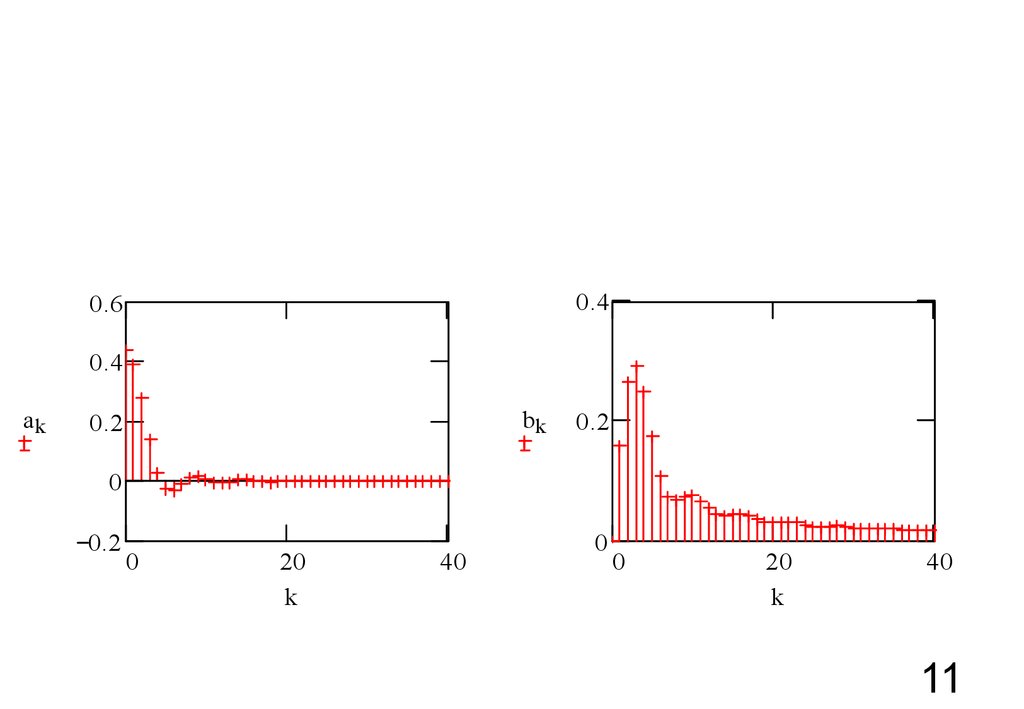
11.
0.40.6
0.4
ak
bk
0.2
0.2
0
0.2
0
20
k
40
0
0
20
k
40
11
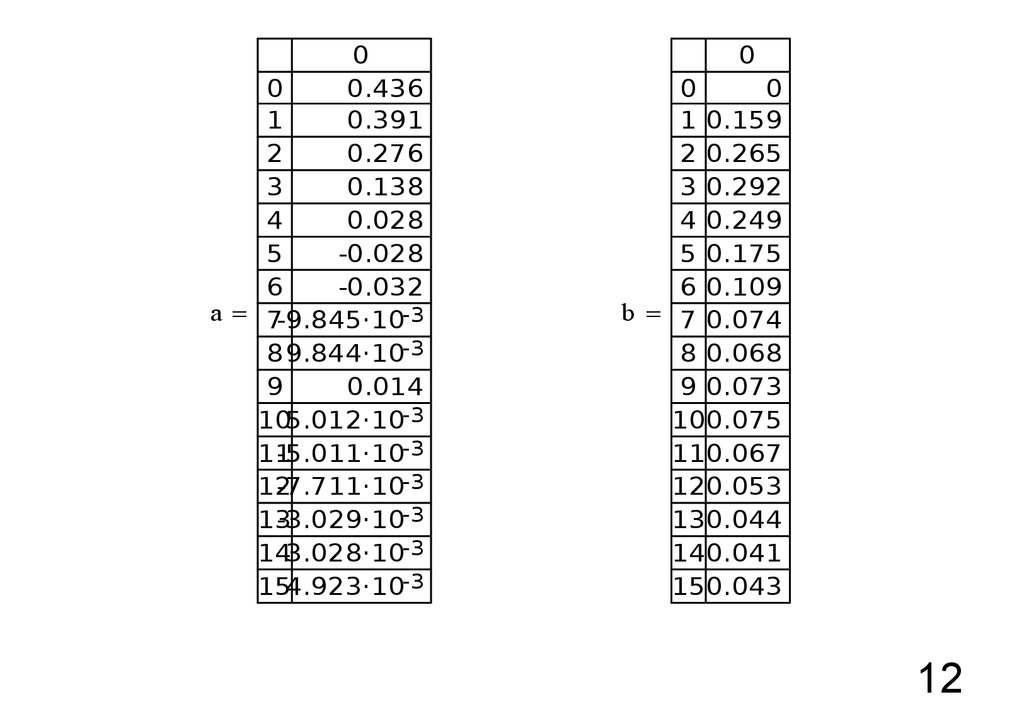
12.
00
0.436
1
0.391
2
0.276
3
0.138
4
0.028
5
-0.028
6
-0.032
a = 7-9.845·10-3
8 9.844·10-3
9
0.014
105.012·10-3
11
-5.011·10-3
12
-7.711·10-3
13
-3.029·10-3
143.028·10-3
154.923·10-3
0
0
0
1 0.159
2 0.265
3 0.292
4 0.249
5 0.175
6 0.109
b = 7 0.074
8 0.068
9 0.073
100.075
110.067
120.053
130.044
140.041
150.043
12
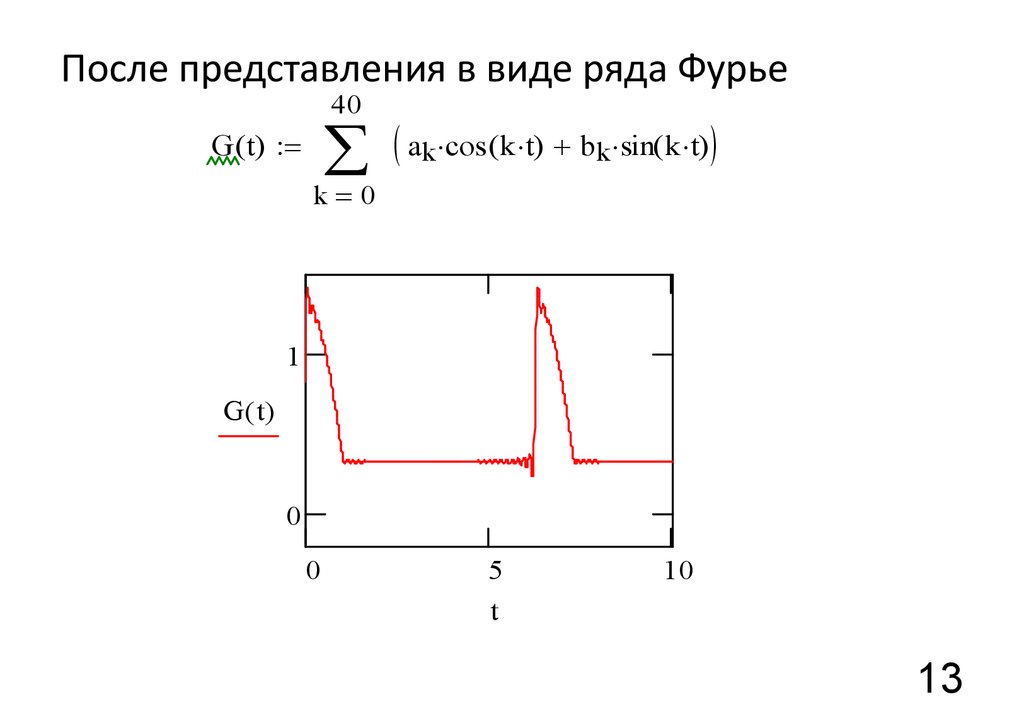
13.
После представления в виде ряда Фурье40
å
G( t) =
( ak cos (k t) + bk sin( k t) )
k=0
1
G( t)
0
0
5
t
10
Ck =
( ak) + ( bk)
2
2
13
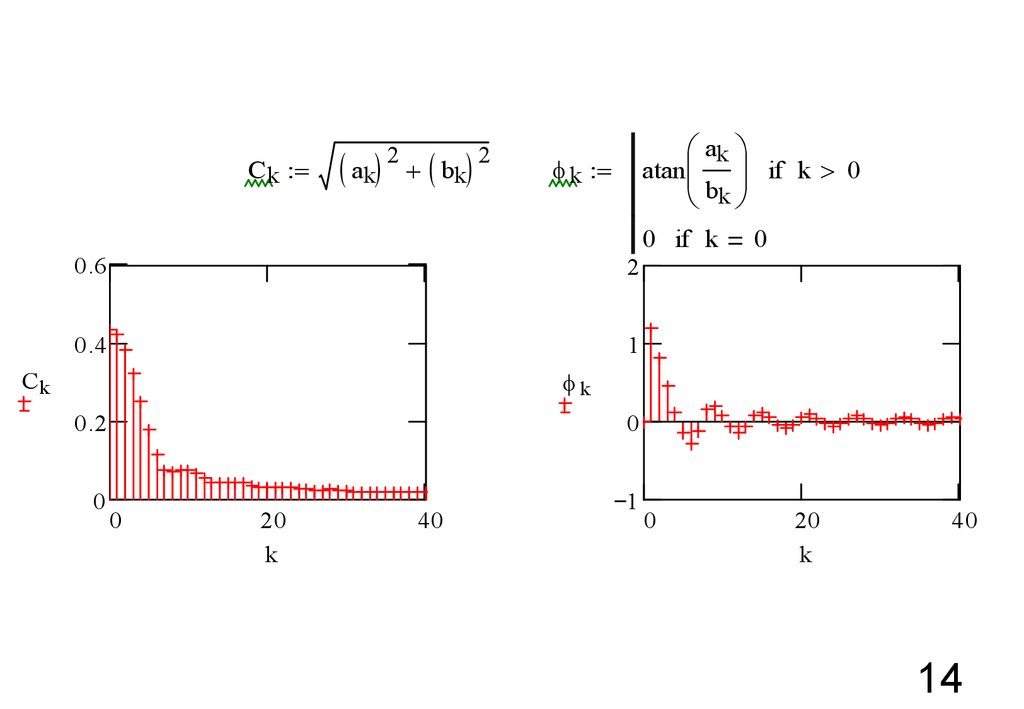
14.
Ck =( ak)
2
+ ( bk)
2
æ ak ö
atanç ÷ if k 0
è bk ø
k =
0 if k
0.6
2
0.4
1
0
k
Ck
0.2
0
0
1
0
20
k
40
0
20
k
40
14
15.
0ck =
1
ak - i bk)
(
2
0
1
2
3
4
5
6
ck = 7
8
9
10
11
12
13
14
15
0.218
0.196
-0.08i
0.138
-0.133i
0.069
-0.146i
0.014
-0.125i
-0.014
-0.088i
-0.016
-0.055i
-3
-4.922·10-0.037i
-3
4.922·10-0.034i
-3
6.892·10-0.037i
-3
2.506·10-0.037i
-3
-2.505·10-0.033i
-3
-3.855·10-0.027i
-3
-1.514·10-0.022i
-3
1.514·10-0.021i
-3
2.461·10-0.022i
15
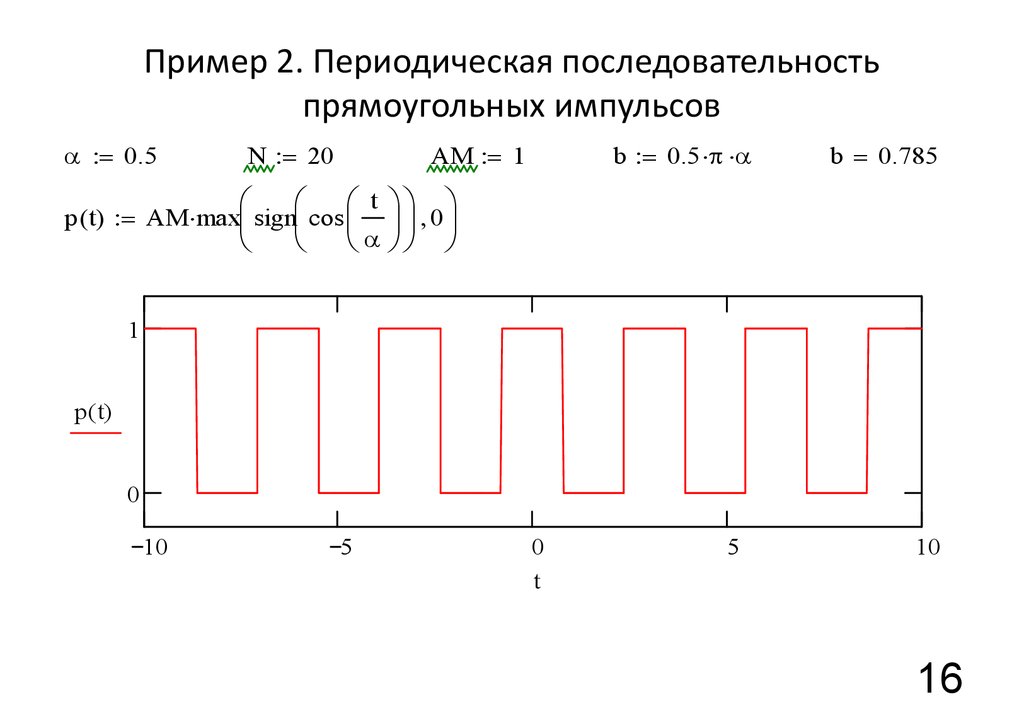
16. Пример 2. Периодическая последовательность прямоугольных импульсов
= 0.5N = 20
æ
è
æ
è
AM = 1
b = 0.5 p
b = 0.785
æ t ö ö 0ö
÷÷ ÷
è øø ø
p ( t) = AM maxç signç cos ç
1
p ( t)
0
10
5
0
t
5
10
16
17.
k = 0 40p
2
vk =
p ( t) cos ( k t) dt
p 0
p
1
v0 =
p ( t) dt
p 0
p
1
wk =
p ( t) sin( k t) dt
p 0
v0 = 0.5
17
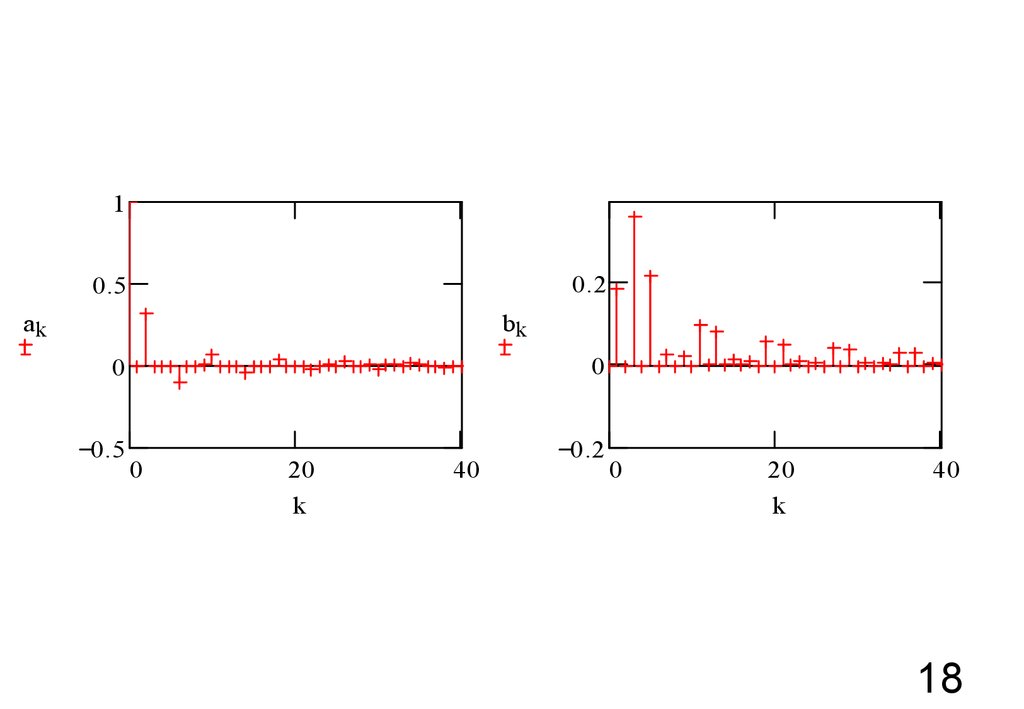
18.
10.2
0.5
ak
bk
0
0
0.5
0
20
k
40
0.2
0
20
k
40
18
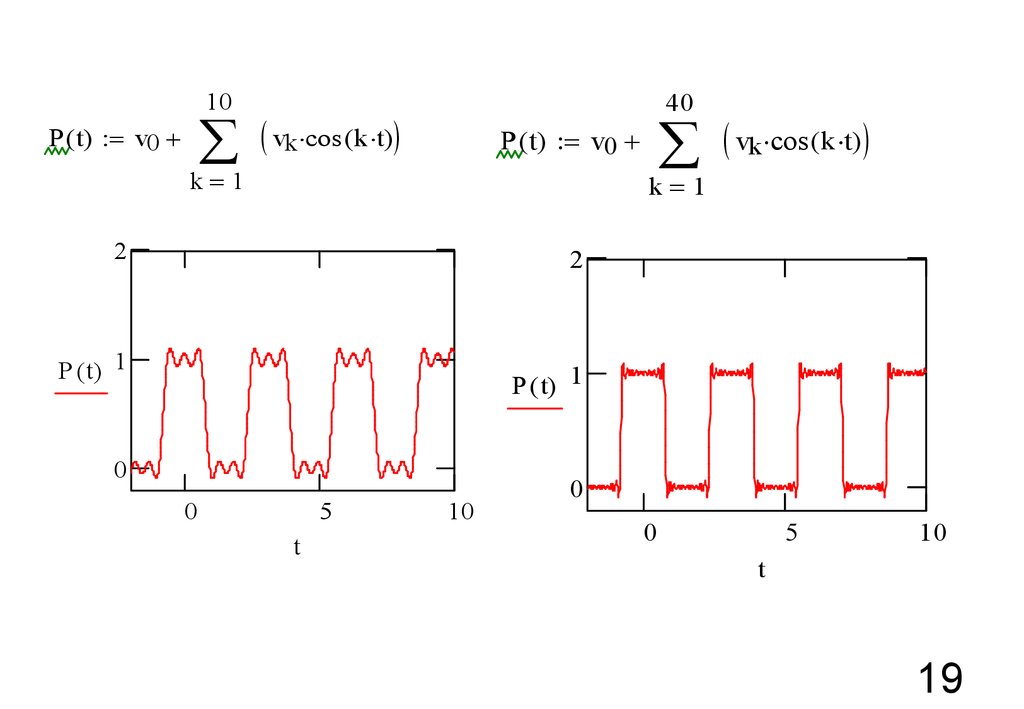
19.
10å
P ( t) = v0 +
40
( vk cos (k t))
å
P ( t) = v0 +
k=1
( vk cos ( k t))
k=1
2
2
P ( t) 1
P ( t) 1
0
0
5
t
10
0
0
5
10
t
19
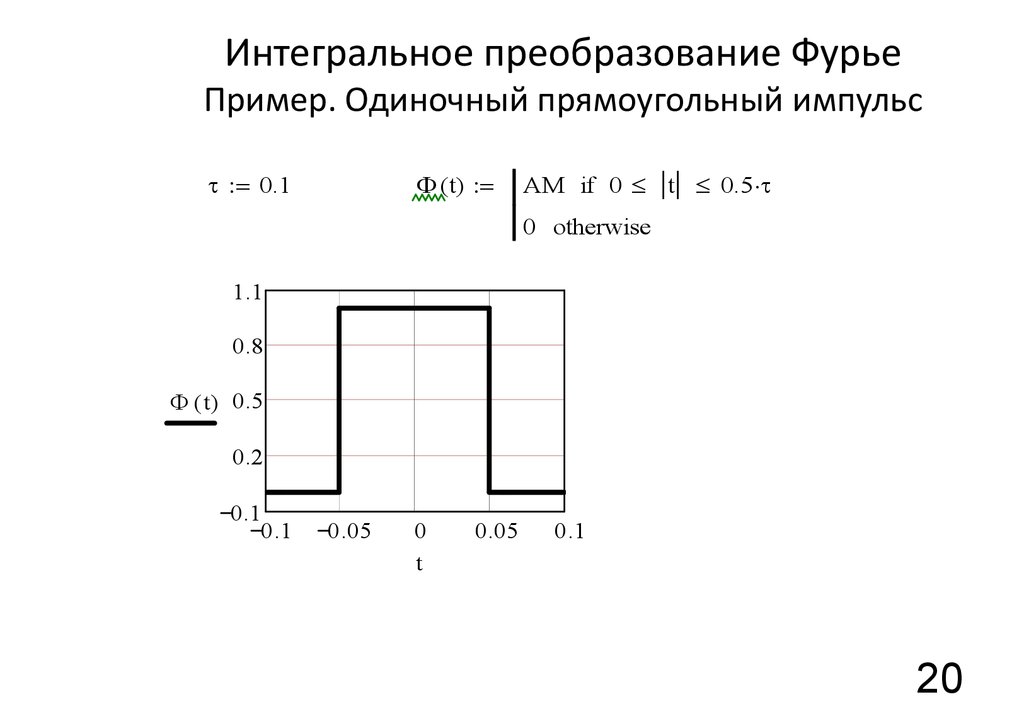
20. Интегральное преобразование Фурье Пример. Одиночный прямоугольный импульс
= 0.1F ( t) =
AM if 0 t 0.5
0 otherwise
1.1
0.8
F ( t) 0.5
0.2
0.1
0.1
0.05
0
t
0.05
0.1
20
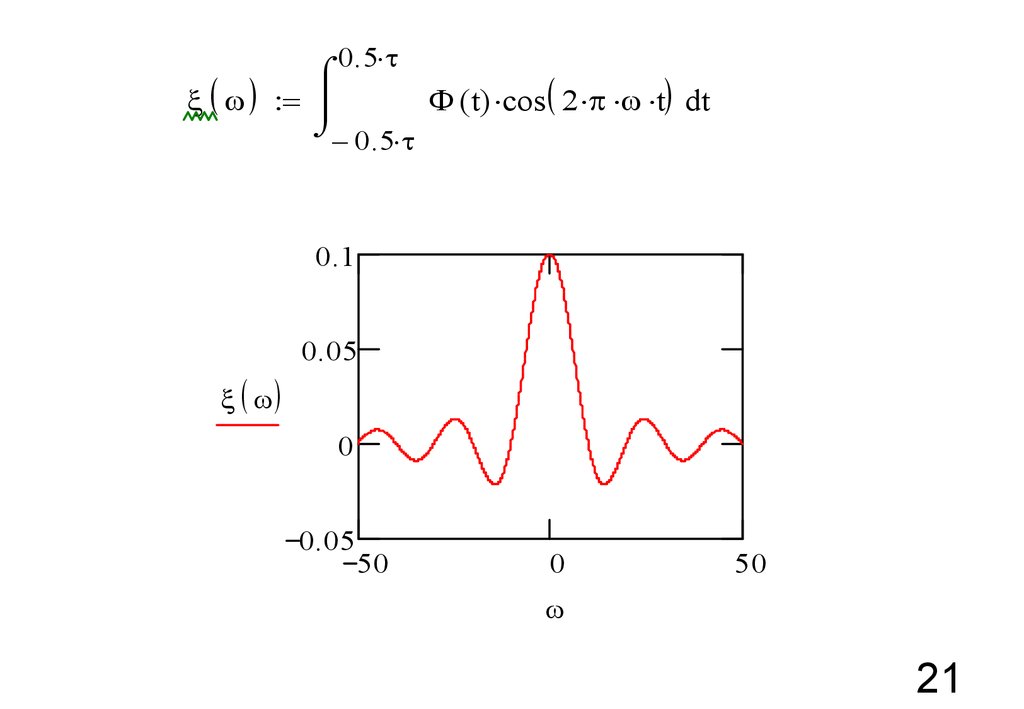
21.
( ) =0.5
F ( t) cos ( 2 p t) dt
- 0.5
0.1
( )
0.05
0
0.05
50
0
50
21
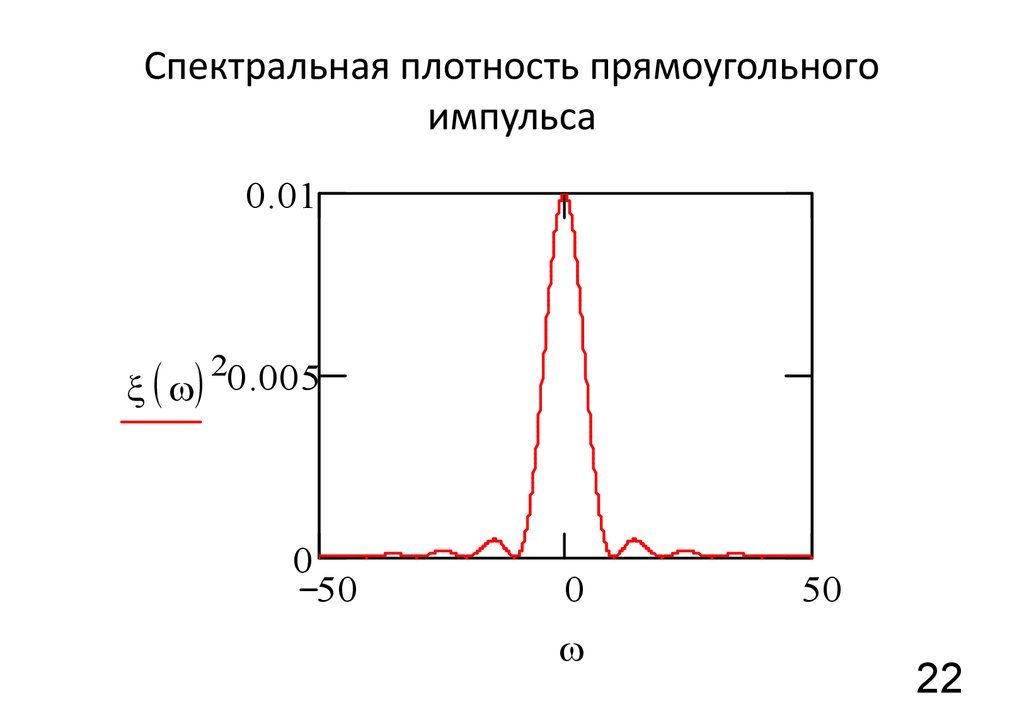
22. Спектральная плотность прямоугольного импульса
0.01( )
20.005
0
50
0
50
22
23. Модели случайных процессов (план) см [1]. Глава 2
Спектральный анализ сигналов• Гауссовский случайный процесс
• Узкополосный стационарный шум
• Узкополосный гауссовский шум
• Узкополосный негауссовский шум
• Диффузионный (винеровский) процесс
• Колебания, модулированные шумом
- амплитудная модуляция
- фазовая модуляция
- частотная модуляция
• Импульсные случайные процессы
23
24. Гауссовский случайный процесс Многомерная гауссовская плотность вероятности
w( x1 , x2 ,..., xN ) =N N
ì
1
ï
= A exp í- å å bk , j ( xk - m k ) x j - m j
ï
î 2 k =1 j =1
(
A=
det( b )
( 2 p)
N 2
.
Смысл параметров гауссовской
плотности вероятности:
)
ü
ï
ý;
ï
þ
xk = m k ;
Kk , j = ( b
-1
)k , j .
24
25. Гауссовский случайный процесс-2
Одномерная плотность вероятностиw( x1 ) =
ì 1
ü
= A exp í - b ( x1 - m1 ) ( x1 - m1 ) ý ;
î 2
þ
b=
1
s2
A=
det( b )
( 2 p)
N 2
=
1
2p s
25
26. Гауссовский случайный процесс-3
Одномерная плотность вероятности примет вид:w( x1 ) =
(
ì 1 1
exp í- 2 x1 - x1
2p s
î 2 s
1
)
2
ü
ý.
þ
В этой формуле все параметры выражены через
экспериментально измеримые величины.
26
27. Гауссовский случайный процесс-4
Свойства одномерного распределения.Отличны от нуля лишь четные центральные моменты
( x - x )n = 1 3 5 ... ( n - 1)sn ; ( nчетное
)
( x - x )n = 0; ( nнечетное
)
( x - x )1 = 0;
( x - x )2 = s2 ;
( x - x )3 = 0;
( x - x )4 = 3 s4 ;
( x - x )5 = 0;
( x - x )6 = 3 5 s6 .
27
28. Гауссовский случайный процесс-5
Реализация в Mathcad.dnorm(x, mu, sigma)
Returns the probability density for the normal distribution with mean
mu and standard deviation sigma.
w ( x) = dnorm ( x 2.5 3)
w1 ( x) = dnorm ( x 5 1)
0.4
0.27
w( x)
w1 ( x)
0.13
10
5
0
5
x
10
15
28
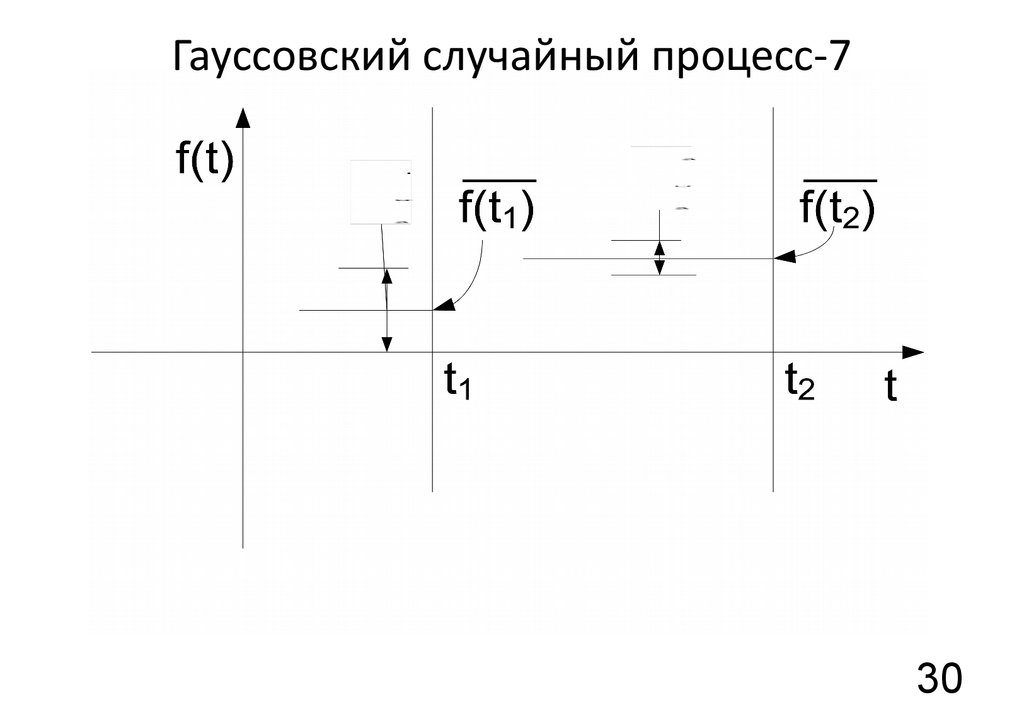
29. Гауссовский случайный процесс-6
Применение для случайных процессов1) x = f ( t )
2 ) w( x ) =
3 ) w( f ,t ) =
(
ì 1 1
exp í- 2 x - x
2p s
î 2 s
1
)
2
ü
ý.
þ
ì
1
ï 1
exp í-
f (t ) - f(t )
2
2 p s( t )
ï
î 2 s( t )
1
(
)
2
ü
ï
ý
ï
þ
29
30. Гауссовский случайный процесс-7
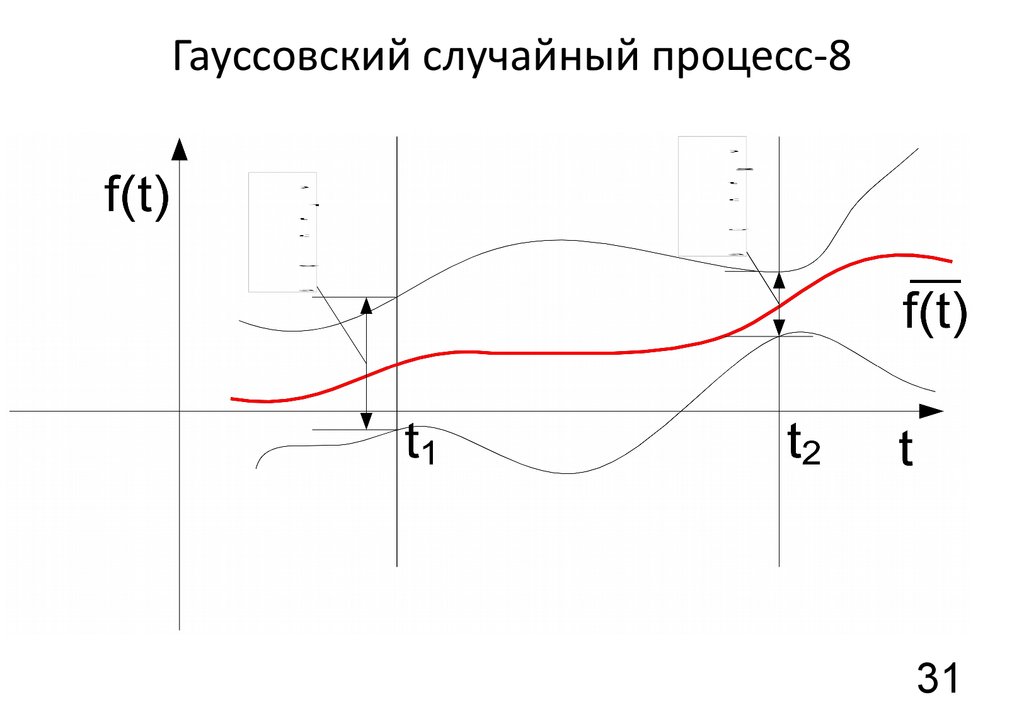
3031. Гауссовский случайный процесс-8
3132. Гауссовский случайный процесс-9
Для вычисления корреляционного момента достаточно парной (для2-х переменных) плотности вероятности
1) w( x1 , x2 ) =
(
)
2
2 ü
ì 1
= A exp í- b11 ( x1 - m1 ) + 2 b12 ( x1 - m1 ) ( x2 - m 2 ) + b22 ( x2 - m 2 ) ý ;
î 2
þ
det( b )
2)A =
.
( 2 p)
det( b ) = b11b2 2 - b12 2 ,
3 ) K12 = ( x1 - m1 ) ( x2 - m2 ) = ( b -1 )12 ;
4 ) K11 = s12 = ( b-1 )11 ; K 2,2 = s2 2 = ( b-1 )22 ;
5 ) K = b-1 .
Наша цель – выразить все параметры через экспериментально измеримые
данные
32
33. Гауссовский процесс-10
æb1) b$ = ç 11
è b21
b12 ö
$
÷ , det( b ) = b11b22 - b12 b21
b22 ø
Ù
-1
Ù
2) K = b
Ù
-1
3) b
4 ) K11
æ b22 -b12 ö æ D1 K ö
=
ç
÷=ç
÷.
$
-b
b
K
D
det( b ) è 21
11 ø
è
2 ø
b22
b11
-b12
=
= D1 , K 22 =
= D2 , K12 =
=K
$
$
$
det( b )
det( b )
det( b )
1
Ù
-1
5 ) det( b
)=
7 ) det( b$ ) =
1
det( b$ )
1
= D1D2 - K
s12 s2 2 (1 - R 2 )
æ D2
$
9 ) b = det( b ) ç
è -K
;
2
2
= D1D2 (1 - R ),
K2
K
6 )R =
;R=
D1D2
s1 s2
2
8 ) D1 = s12 ; D2 = s2 2
æ s2 2
-K ö
1
ç
÷=
D1 ø s12 s2 2 (1 - R 2 ) çè -K
æ 1
ç
2
s
-K ö
1
1
ç
÷=
2
s12 ÷ø (1 - R ) ç - R
çç
è s1s2
-
R ö
s1 s2 ÷
÷
1 ÷
÷
s2 2 ÷ø
33
34. Гауссовский процесс-11
Таким образом, плотность вероятности может быть выраженачерез экспериментально измеримые величины:
w( x1 , x2 ) =
=
1
2 ps1s2 1 - R 2
(
ì
æ x -x
1
1
ï
ç 1
exp í ç
2
2
2(1
R
)
s
ï
ç
1
è
î
)
2
(
-2R
x1 - x1
)(
x2 - x2
s1s2
) +(
x 2 - x2
s2 2
)
2
öü
֕
÷ý ;
֕
øþ
Рассмотрим применение распределения для описания
случайных процессов
x1 = f ( t1 ), x2 = f ( t2 )
34
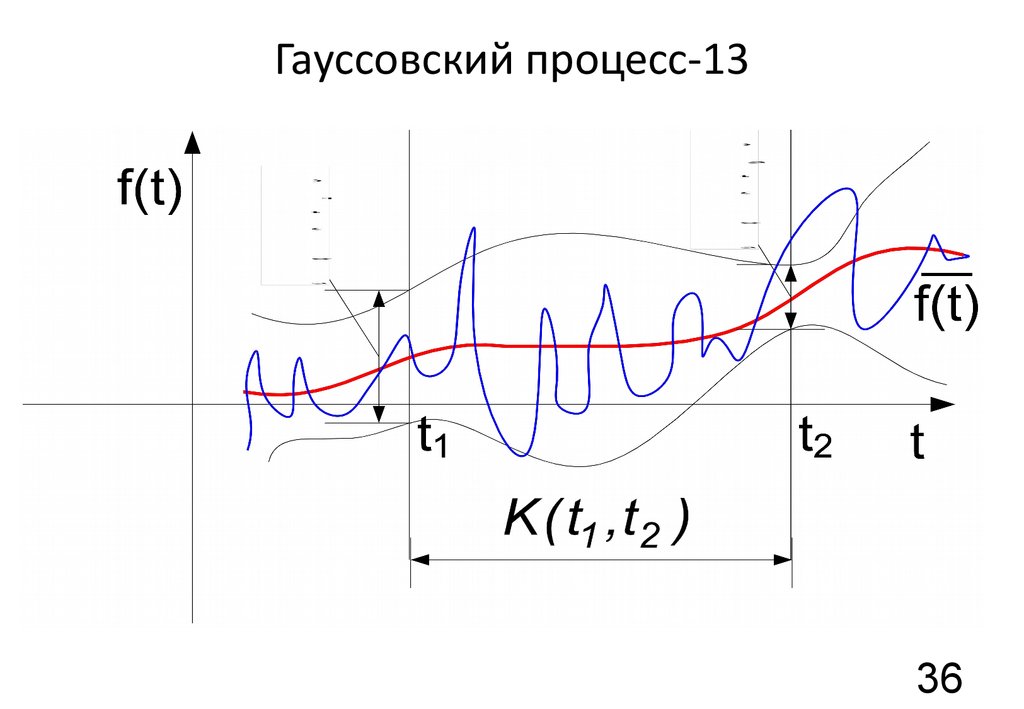
35. Гауссовский процесс-12
x1 = f ( t1 ), x2 = f ( t 2 );(
)
(
2
D( t1 ) = f ( t1 ) - f ( t1 ) ; D( t 2 ) = f ( t 2 ) - f ( t 2 )
)
2
K12 = ( x1 - x1 )( x2 - x2 );
(
)(
)
K( t1 ,t2 ) = f ( t1 ) - f ( t1 ) f ( t 2 ) - f ( t 2 ) .
35
36. Гауссовский процесс-13
3637. Гауссовский случайный процесс-14
Выводы:1. Если процесс гауссовский, то все его
характеристики можно вычислить. Любые
моменты (средние) выражаются через
параметры m и b.
2. Для стационарного гауссовского процесса
параметры m и b не зависят от времени.
37
38. Модели случайных процессов (план) см [1]. Глава 2
Спектральный анализ сигналовГауссовский случайный процесс
• Узкополосный стационарный шум
• Узкополосный гауссовский шум
• Узкополосный негауссовский шум
• Диффузионный (винеровский) процесс
• Колебания, модулированные шумом
- амплитудная модуляция
- фазовая модуляция
- частотная модуляция
• Импульсные случайные процессы
38
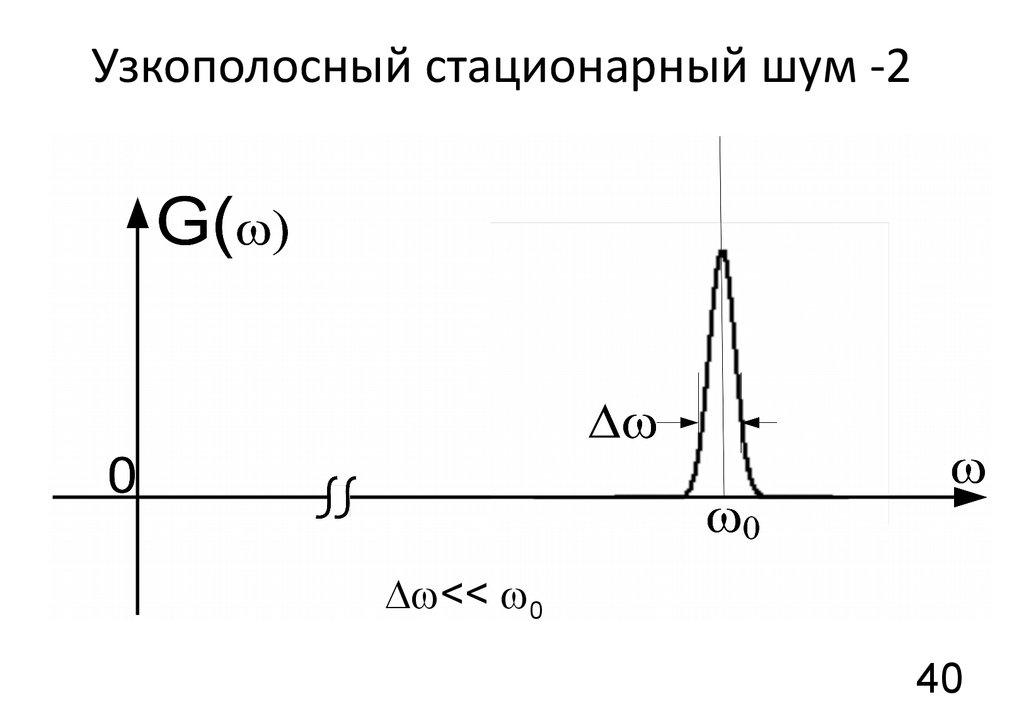
39. Узкополосный стационарный шум
Шум узкополосный, если спектральная плотностьG( ) отлична от нуля в узкой области частот
вблизи некоторой частоты 0:
<< 0
в виде колебаний, близких к гармоническим
39
40. Узкополосный стационарный шум -2
<< 040
41. Узкополосный стационарный шум -2
Флуктуационную компоненту представим в виде(модель узкополосного шума):
(t ) = (t ) cos [ 0t + j (t ) ] ,
где
(t) – огибающая (амплитуда).
j(t) – фаза.
41
42.
Вместо огибающей и фазы также вводятквадратурные компоненты a(t), b(t)
(t ) = a (t ) cos [ 0t ] - b(t ) sin [ 0t ]
Таким образом, мы выделяем функции времени
• быстрые cos [ 0t ] , sin [ 0t ]
• медленные a(t), b(t) или (t), j(t)
42
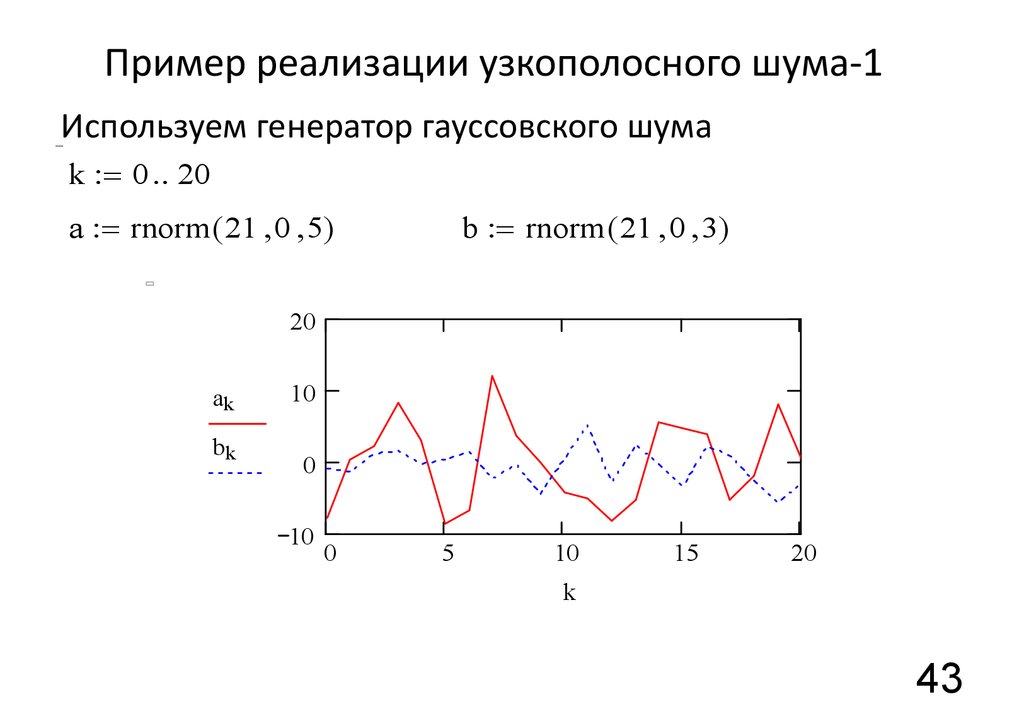
43. Пример реализации узкополосного шума-1
Используем генератор гауссовского шумаk = 0 20
a = rnorm ( 21 0 5)
b = rnorm ( 21 0 3)
20
ak
bk
10
0
10
0
5
10
15
20
k
xk = k
43
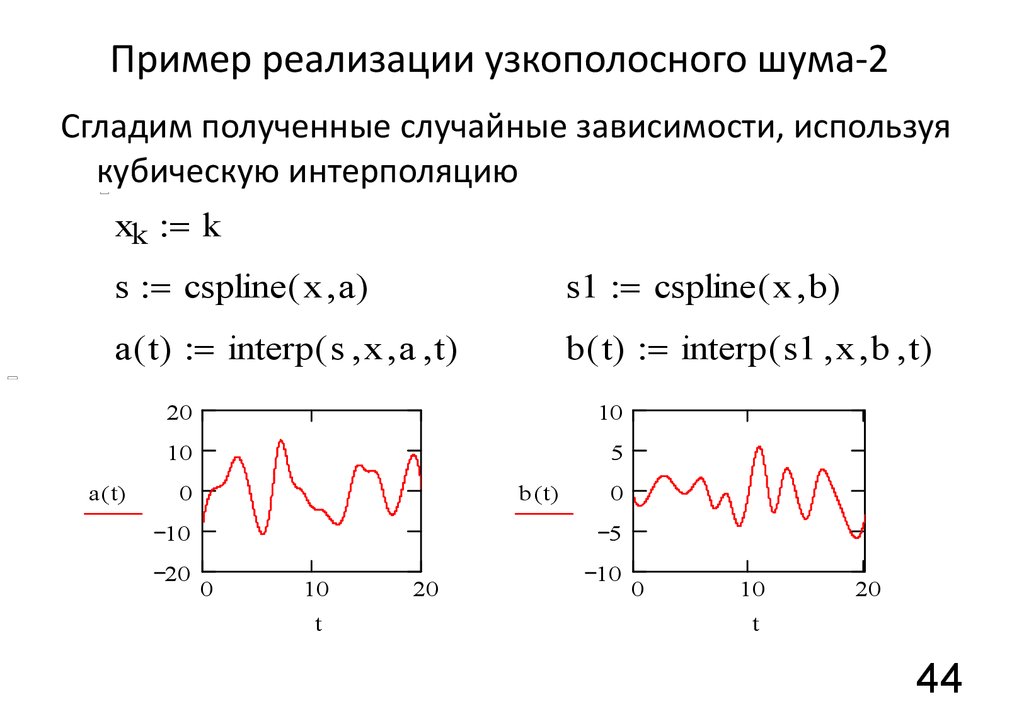
44. Пример реализации узкополосного шума-2
bk0
Пример реализации узкополосного шума-2
10
0
5
10
15 используя
20
Сгладим полученные
случайные
зависимости,
кубическую интерполяцию
k
xk = k
s = cspline ( x a)
s1 = cspline ( x b)
a ( t) = interp ( s x a t)
b ( t) = interp ( s1 x b t)
a ( t)
20
10
10
5
0
b ( t)
10
20
0
5
0
10
t
20
10
0
10
20
t
44
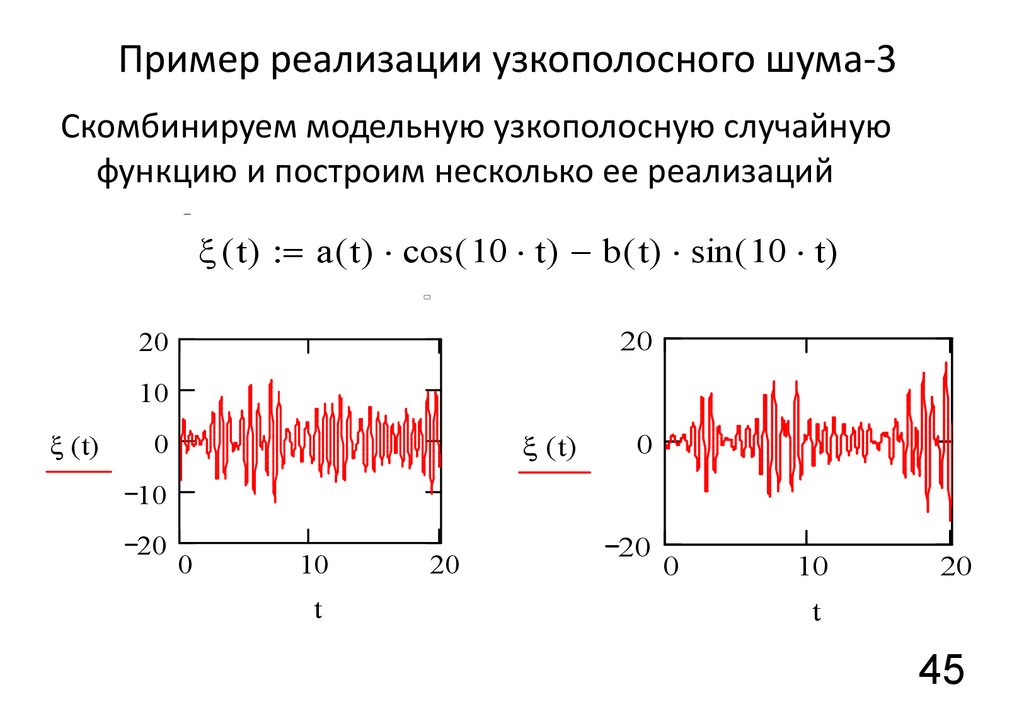
45. Пример реализации узкополосного шума-3
Скомбинируем модельную узкополосную случайнуюфункцию и построим несколько ее реализаций
( t) = a ( t) cos ( 10 t) - b ( t) sin ( 10 t)
20
20
10
( t)
( t)
0
0
10
20
0
10
t
20
20
0
10
20
t
45
46. Постановка задачи:
Задача: зная свойства шума (t) найтистатистические характеристики огибающей и
фазы или квадратурных компонент.
Все рассматриваемые случайные процессы
• Сам шум
• Его амплитуда и фаза
• Квадратурные компоненты
Считаются стационарными случайными функциями
времени.
46
47. Корреляционные и спектральные характеристики квадратурных компонент
• Предполагаем, что• Так как
.=0
(t ) = a (t ) cos ( 0t ) - b(t ) sin ( 0t )
то a = 0, b = 0
Переходим к анализу корреляционной функции
47
48.
Считаем известной корреляционную функциюK ( ) =
Подставим в эту формулу представление
квадратурные компоненты
(t )
через
K ( ) = =
= éë a (t ) cos ( 0t ) - b(t ) sin ( 0t ) ùû éë a (t + ) cos ( 0 (t + ) ) - b(t + ) sin ( 0 (t + ) ) ùû =
= éë a cos ( 0t ) - b sin ( 0t ) ùû éë a cos ( 0 (t + ) ) - b sin ( 0 (t + ) ) ùû =
= aa cos ( 0t ) cos ( 0 (t + ) ) + bb sin ( 0t ) sin ( 0 (t + ) ) -ba sin ( 0t ) cos ( 0 (t + ) ) - a b cos ( 0t ) sin ( 0 ( t + ) ) .
aa = a (t )a (t + );
bb = b(t )b(t + );
ab = a (t )b(t + );
ba = b(t )a (t + ).
48
49.
Учтем известные тригонометрические формулы1
[ cos( 0 ) + cos( 0 (2t + ) ] ;
2
1
sin ( 0t ) sin ( 0 (t + ) ) = [ cos( 0 ) - cos( 0 (2t + ) ] ;
2
1
sin ( 0t ) cos ( 0 (t + ) ) = [ - sin( 0 ) + sin( 0 (2t + ) ] ;
2
1
cos ( 0t ) sin ( 0 (t + ) ) = [ sin( 0 ) + sin( 0 (2t + ) ] ;
2
cos ( 0t ) cos ( 0 (t + ) ) =
Подставим эти выражения в приведенное выше выражение K ( )
49
50.
K ( ) =1
=
aa + bb cos ( 0 ) + ba - ab sin ( 0 ) +
2
{(
)
(
(
)
)
(
)
+ aa - bb cos ( 0 (2t + ) ) + ba + ab sin ( 0 (2t + ) )
}
В силу стационарности здесь не должно быть явной зависимости от
времени, поэтому
1)
aa = bb = s 2 p ( );
aa = bb = s 2 = .
2)
Здесь
p ( )
q ( )
Это следует из
равноправности амплитуд
ab = -ba = s 2 q ( )
p ( ) и q ( ) некоторые пока неизвестные функции.
Чётная функция аргумента
Нечётная функция аргумента
50
51.
K ( ) == s 2 p ( ) cos ( 0 ) - s 2 q( ) sin ( 0 ) =
= s 2 éë p ( ) cos ( 0 ) - q ( ) sin ( 0 ) ùû .
Таким образом, получили :
K ( ) = s 2 éë p ( ) cos ( 0 ) - q( ) sin ( 0 ) ùû
K ( ) = s 2 R ( )
R ( ) = p( ) cos ( 0 ) - q ( ) sin ( 0 ) =
= r ( ) cos [ 0 + y ( ) ]
Где введена безразмерная корреляционная функция
R ( )
51
52. Чтобы найти неизвестные функции воспользуемся формулой Винера-Хинчина:
Чтобы найти неизвестные функции p ( ), q ( ),воспользуемся формулой Винера-Хинчина:
K ( ) =
¥
ò
G ( )e - i d =
-¥
¥
ò G( ) ( cos - i sin ) d .
-¥
G ( ) = G ( - ).
¥
Интеграл от нечетной функции (содержит sin( )) равен
нулю. В силу четности можно ограничиться интегралом
¥
от 0 до ¥
K ( ) = 2 ò G ( ) cos d = ò G + ( ) cos d
0
0
W = - 0
K ( ) =
¥
ò
-
Сдвиг начала координат в точку 0.
G + (W + 0 ) cos( W + 0 ) d W
0
52
53.
K ( ) =¥
ò
¥
=
ò
-
G + (W + 0 ) cos(W + 0 ) d W =
0
G + (W + 0 )[cos(W ) cos( 0 ) - sin(W ) sin( 0 )] d W =
0
¥
ò
= cos( 0 )
-
G + (W + 0 ) cos(W ) d W - sin( 0 )
0
¥
ò
-
G + (W + 0 ) sin(W ) d W.
0
Сравнивая с полученным ранее выражением, найдем
¥
ò
s 2 p ( ) =
-
s 2 q ( ) =
0
¥
ò
-
G + (W + 0 ) cos(W ) d W
G + (W + 0 ) sin(W ) d W
0
53
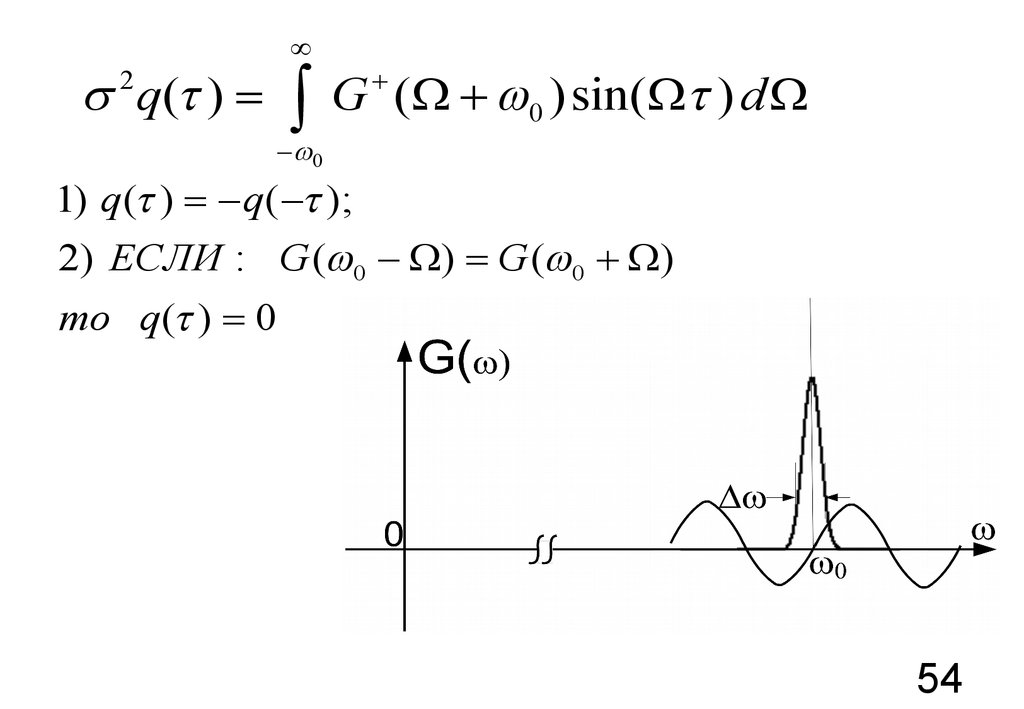
54.
¥s q( ) =
2
ò
-
G (W + 0 ) sin(W ) d W
+
0
1) q( ) = - q( - );
2) ЕСЛИ : G ( 0 - W) = G ( 0 + W)
то q( ) = 0
54
55. При этом предположении
K ( ) = s 2 éë p ( ) cos ( 0 ) - q( ) sin ( 0 ) ùûK ( ) = s 2 p ( ) cos ( 0 )
¥
s 2 p ( ) =
ò
-
G + (W + 0 ) cos(W ) d W
0
aa = bb = s p ( )
2
p( )
Имеет свойства корреляционной функции
55
56. Модели случайных процессов (план) см [1]. Глава 2
Спектральный анализ сигналовГауссовский случайный процесс
Узкополосный стационарный шум
• Узкополосный гауссовский шум
• Узкополосный негауссовский шум
• Диффузионный (винеровский) процесс
• Колебания, модулированные шумом
- амплитудная модуляция
- фазовая модуляция
- частотная модуляция
• Импульсные случайные процессы
56
57. Узкополосный стационарный гауссовский шум
(t ) = a (t ) cos( 0t ) - b(t ) sin( 0t )a = 0; b = 0; ab = 0
a 2 = b2 = 2 = s 2
1
w( a , b ) =
e
2
2ps
a 2 + b2
2s 2
57
58.
Найдем плотность вероятности переменныхw( , j )d dj = w( a, b) a = cos(j )
b = sin(j )
a = cos(j ),
b = sin(j ) ,
æ ¶a ö ö
ç
÷ ÷
¶
j
è
ø ÷ æ cos(j )
÷ = ç sin(j )
æ ¶b ö ÷ è
ç
÷ ÷
¶
j
è
ø ø
= [ cos(j ) ] 2 + [ sin(j ) ] 2 = ;
b = sin(j )
иj
¶ ( a , b)
d dj
¶( ,j )
æ æ ¶a ö
çç
÷
¶
øj
¶ ( a , b) ç è
=ç
¶( ,j )
ç æç ¶b ö÷
ç è ¶ ø
j
è
w(a, b) a = cos(j )
- sin(j ) ö
÷=
cos(j ) ø
æ a 2 + b2 ö
æ 2 ö
1
1
=
exp ç =
exp ç ÷
2
2
2
2 ÷
2ps
2
s
2
ps
2
s
è
ø a= cos(j )
è
ø
b = sin( j )
æ 2
1
w( , j )d dj =
exp ç 2
2
2ps
2
s
è
ö
÷ d dj
ø
58
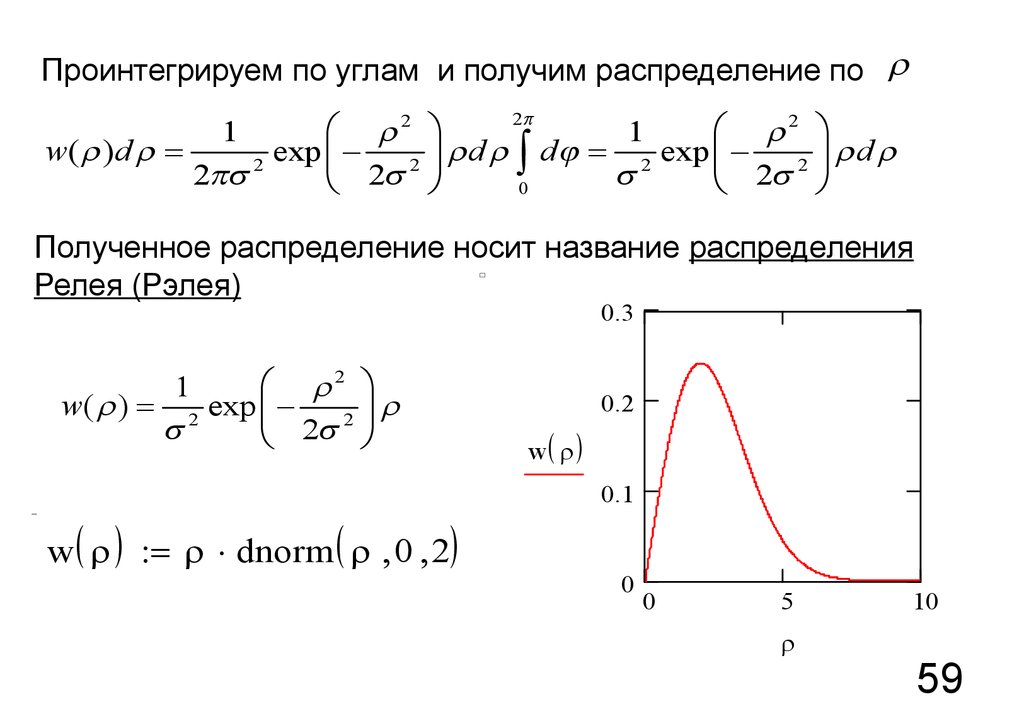
59.
Проинтегрируем по углам и получим распределение поæ 2
1
w( )d =
exp ç 2
2
2ps
2
s
è
2p
ö
æ 2
1
÷ d ò dj = 2 exp ç 2
s
2
s
ø
è
0
ö
÷ d
ø
Полученное распределение носит название распределения
Релея (Рэлея)
0.3
æ 2
1
w( ) = 2 exp ç 2
s
2
s
è
ö
÷
ø
0.2
w( )
0.1
w ( ) = dnorm ( 0 2)
0
0
5
10
59
60.
Моменты распределения Рэлея:æ 2
1
w( ) = 2 exp ç 2
s
2
s
è
ö
÷ .
ø
¥
2 n = ò 2 n w( ) d = 2 n n !s 2 n ;
0
2 n +1
¥
=ò
2 n +1
0
1
=
1
=
p
w( ) d =
(2n + 1)!!s 2 n +1 ;
2
p 1
;
2s
2 1
;
p s
1
p
= .
2
60
61.
Используем полученные результаты для анализасуперпозиции гармонического сигнала и гауссовского шума.
Случайный процесс имеет вид «Сигнал» + «Шум»
1) x(t ) = S (t ) + (t ).
2) S (t ) = aS (t ) cos( 0t ) - bS (t ) sin( 0t ) = S cos [ 0t + j S (t ) ] ;
3) (t ) = a(t ) cos( 0t ) - b(t ) sin( 0t );
4) x(t ) = [ aS (t ) + a(t ) ] cos( 0t ) - [ bS (t ) + b(t ) ] sin( 0t ) =
= (t ) cos [ 0t + j (t ) ] .
Далее для краткости опустим временной аргумент
5) =
( a + aS )
2
+ ( b + bS ) ;
2
6) a = cos j - aS ; 7) b = sin j - bS .
61
62.
Будем искать вероятностные характеристики огибающей ифазы, и j процесса х(t).
Исходим из распределения квадратурных компонент шума:
1
w( a, b) =
e
2
2ps
a 2 + b2
2s 2
Так как
a = cos j - aS ; b = sin j - bS .
якобиан имеет прежний вид
æ æ ¶a ö
çç
÷
¶ (a, b) ç è ¶ øj
=ç
¶( ,j )
ç æç ¶b ö÷
ç è ¶ ø
j
è
æ ¶a ö ö
ç
÷ ÷
è ¶j ø ÷
÷ = .
æ ¶b ö ÷
ç
÷ ÷
¶
j
è
ø ø
62
63.
a + b = ( cos j - aS ) + ( sin j - bS ) =2
2
2
2
= 2 - 2 (aS cos j + bS sin j ) + aS 2 + bS 2 =
= 2 - 2 S cos(j - j S ) + S 2 .
1
w(a, b) =
e
2
2ps
a 2 +b2
2s 2
ì 2 - 2 S cos(j - j S ) + S 2 ü
1
w( , j ) =
exp íý
2
2
2ps
2s
î
þ
Будем искать распределение по
63
64.
w( ) =2p
ò w( , j )dj =
0
2p
ì 2 - 2 S cos(j - j S ) + S 2 ü
ý=
2
ò0 dj exp íî2s
þ
ì 2 + S 2 ü
æ S ö
= 2 I 0 ç 2 ÷ exp íý.
2
s
2s
è s ø
î
þ
1
=
2
2ps
æ S ö
Где I 0 ç 2 ÷ модифицированная функция Бесселя.
è s ø
I n ( xудовлетворяет
)
дифференциальному уравнени ю Бесселя
x 2 y¢¢ + xy ¢ - ( x 2 + n 2 ) y = 0.
p
(-1) n
x cos j
I n ( x) =
e
cos nj dj
ò
p 0
64
65.
x = - 5 - 4.99995
40
I0 ( x )
I1 ( x )
20
0
20
5
0
x
5
Более подробно о модифицированной функции Бесселя см.
Ю.Н. Бронштейн и К.А.Семендяев «Справочник по
математике для инженеров и учащихся вузов» С. 464.
65
66.
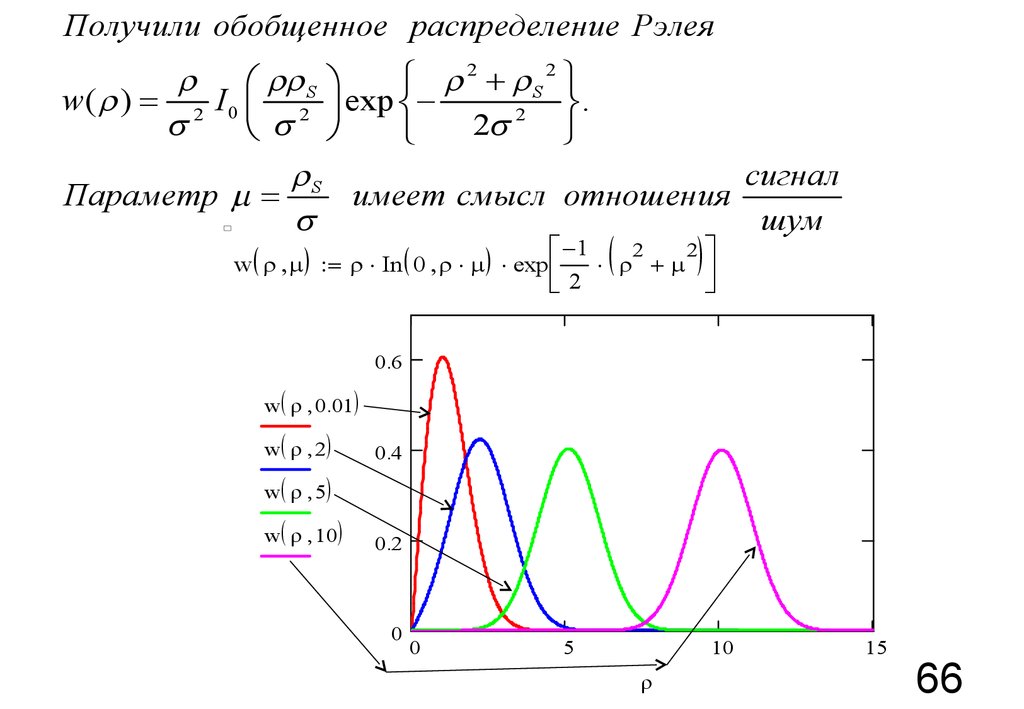
Получили обобщенное распределение Рэлеяì 2 + S 2 ü
æ S ö
w( ) = 2 I 0 ç 2 ÷ exp íý.
2
s
2s
è s ø
î
þ
S
сигнал
Параметр m =
имеет смысл отношения
s
шум
é -1 ( 2 + m 2) ù
w ( m ) = In ( 0 m ) exp
ë2
û
0.6
w ( 0.01)
w ( 2)
0.4
w ( 5)
w ( 10)
0.2
0
0
5
10
15
66
67.
Замечание об использовании Mathcad.В Mathcad имеется специальная функция
In ( m x)
Returns the m-th order modified Bessel function of the first
kind. x must be real. m must be between 0 and 100 inclusive.
Именно этот оператор использовался выше.
67
68. Обсуждение результатов
В пределе сильного шума, когда m<<1 обобщенноераспределение Рэлея близко к обычному распределению Рэлея
æ S
w( ) = 2 I 0 ç 2
s
è s
1) m ® 0
ì
ü
ì 2 + S 2 ü
ï 1 æ 2
ö
æ m ö
2 öï
ý = 2 I0 ç
÷ exp í- ç 2 + m ÷ ý .
÷ exp í2
2s
è s ø
ø
ï
øï
î
þ s
î 2 ès
þ
2
ì
ù
ï 1 æ 2 öü
ïé
2
2
w( ) » 2 exp í- ç 2 ÷ ý 1 - m + m
.
2
s
2s û
ï
î 2 è s øï
þë
2) m ® ¥
w( ) =
2
ì
ü
1
ï (
S ) ï
exp íý
2
2
s
2ps
ï
ï
î
þ
68
69. Распределение фазы
¥w(j ) = ò w( , j )d =
0
{
}
1 -m2
z2
=
e
1 + p ze [ 1 + F ( z ) ] .
2p
z = m cos(j - j S ),
2
F( z ) =
p
z
òe
-t 2
dtинтеграл
вероятности
0
или функция ошибок erf(z)
69
70. В предельных случаях
{}
1 -m2
z2
w(j ) =
e
1 + p ze [ 1 + F ( z ) ] .
2p
1) m ® 0
1
m
m2
w(j ) »
+
cos(j - j S ) +
cos 2(j - j S ).
2p 2 p
2p
2) m ® ¥
m
w(j ) »
exp éë - m 2 (j - j S ) 2 ùû .
p
70
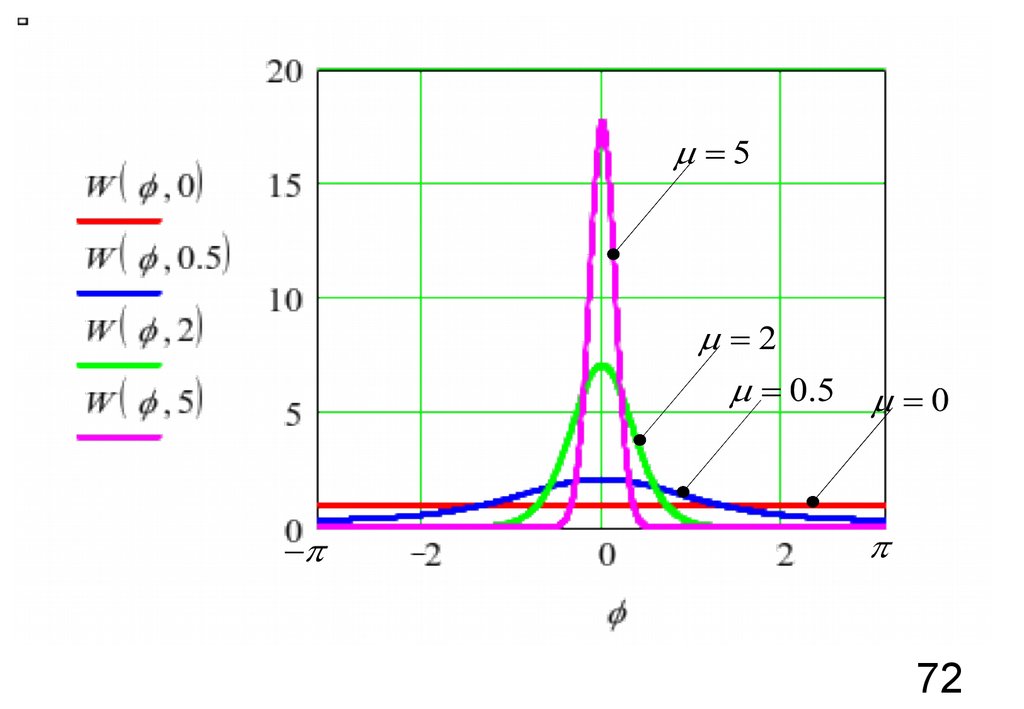
71. Построение графика W(,) средствами Mathcad
Построение графика W( ,m) средствами Mathcadz ( m ) = m cos ( )
W ( m ) = e
-m
2
2
é
ù
(
)
z
m
ë 1 + p z ( m) e
( 1 + erf ( z ( m ) ) ) û ,
где использована специальная функция (Function Category - Special)
erf(z)
Returns the error function.
71
72.
7273.
Модели случайных процессов (план)см [1]. Глава 2
Спектральный анализ сигналов
Гауссовский случайный процесс
Узкополосный стационарный шум
Узкополосный гауссовский шум
• Узкополосный негауссовский шум (ознакомиться
самостоятельно!)
• Диффузионный (винеровский) процесс
• Колебания, модулированные шумом
- амплитудная модуляция
- фазовая модуляция
- частотная модуляция
• Импульсные случайные процессы
73
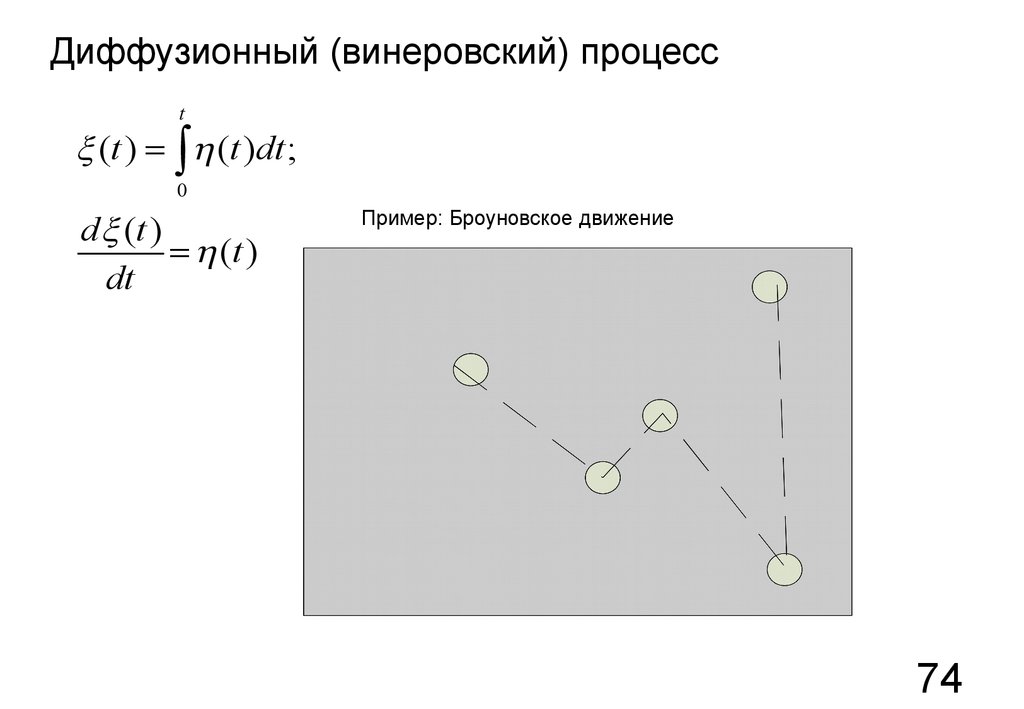
74.
Диффузионный (винеровский) процессt
(t ) = ò h (t )dt ;
0
d (t )
= h (t )
dt
Пример: Броуновское движение
74
75.
d (t )d (t )
m
= -l
+ h (t ).
2
dt
dt
Если пренебречь инерцией
2
d 2 (t )
d (t )
m
= -l
+ h (t ).
2
dt
dt
d (t )
= h (t ),
dt
переопределение времени
t := t / l
75
76.
Постановка задачи:найти вероятностные свойства процесса (t), зная свойства
процесса h(t).
Пусть известно, что:
h (t ) = 0; h (t ) 2 = s 02 ;
h (t )h (t + ) = K 0 ( ) =
¥
ò
G0 ( )ei t d
-¥
Требуется найти:
(t ) = ? (t )
2
=s =?
2
(t ) (t + ) = K (t , ) =
¥
ò G( )e
i t
d = ?
-¥
76
77.
t1) (t ) = ò h (t ) dt = 0;
0
(t ) = 0 ;
2) (t ) 2 = s 2 =
t
t
òh (q )dq òh (q ¢)dq ¢
0
=
0
t
t
t
t
0
0
0
0
= ò dq ò dq ¢ h (q )h (q ¢) = ò dq ò dq ¢K 0 ( );
= q - q ¢.
t
t
0
0
s 2 = ò dq ò dq ¢K 0 ( ).
77
78.
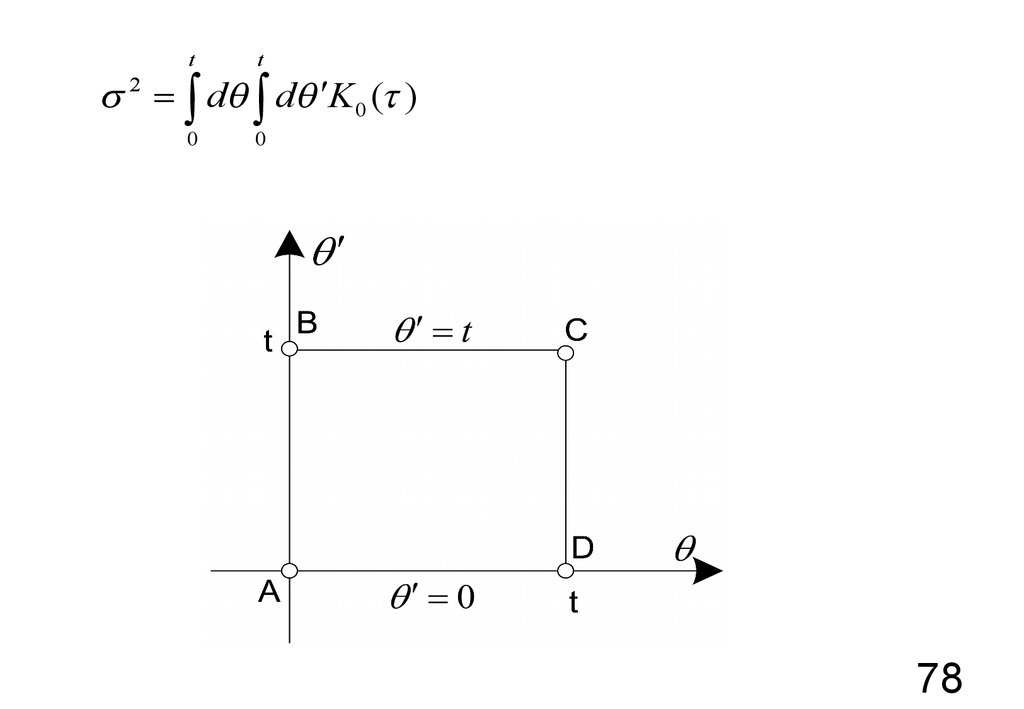
tt
0
0
s 2 = ò dq ò dq ¢K 0 ( )
78
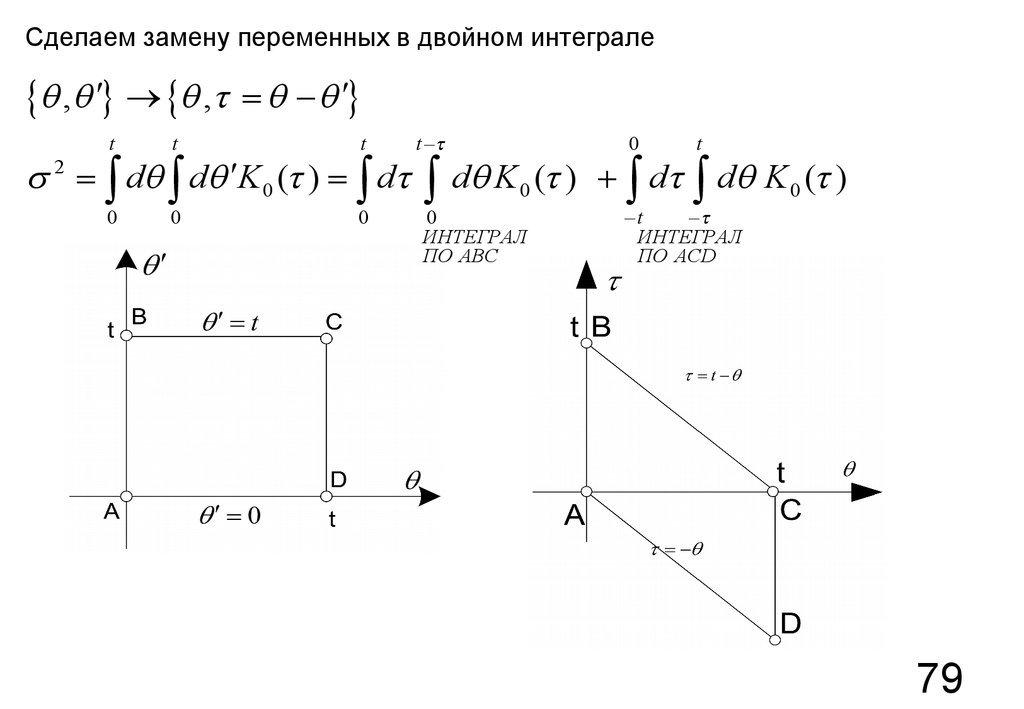
79.
Сделаем замену переменных в двойном интеграле{ q ,q ¢}
t
® { q , = q - q ¢}
t
t
s 2 = ò dq ò dq ¢K 0 ( ) = ò d
0
0
0
t -
ò dq K
0
0
0
ИНТЕГРАЛ
ПО АВС
( ) + ò d
t
ò dq K
0
( )
-t
ИНТЕГРАЛ
ПО ACD
79
80.
tt -
0
t
é
ù
2
s = ò dq ò dq ¢K 0 ( ) = ò d ò dq + ò d ò dq K 0 ( ) =
0
0
0
-t
-
ë0
û
после интегрирования по q получим
t
t
0
ét
ù
= ò d (t - ) + ò d (t + ) K 0 ( ) =
ë 0
û
-t
во втором интеграле сделаем замену ® - ,
учитывая , что K 0 ( ) = K 0 ( - )
t
ét
ù
= ò d (t - ) + ò d (t - ) K 0 ( );
0
ë0
û
t
s 2 = 2 ò d (t - ) K 0 ( ).
(Å)
0
80
81.
t1) s 2 = 2 ò d (t - ) K 0 ( );
0
2) K 0 ( ) =
¥
ò G ( )e
i
0
d ;
-¥
¥
t
-¥
0
3) s 2 = 2 ò d G0 ( ) ò d (t - )ei .
4) ¢ = t - , d ¢ = - d ,
t
0
t
0
t
0
5) ò d (t - )ei = - ò d ¢ ¢ei (t - ¢) = ei t ò d ¢ ¢e - i ¢ =
t - i t ù i t
1
é 1 - i t
= 2 (e
- 1) e e = 2 ( 1 + i t - ei t )
i
ë
û
81
82.
¥1
s = 2 ò G0 ( ) 2 ( 1 + i t - ei t ) d =
-¥
2
¥
(
)
1
= 2 ò G0 ( ) 2 1 + i t - cos( t ) - i sin( t ) d =
-¥
из - за четности G0 ( ) перечёркнутые слагаемые
не дадут вклада в интеграл;
2
æ
æ t ö ö
1 - cos( t ) = 2 ç sin ç ÷ ÷ ;
è 2 øø
è
2
æ
æ t ö ö
¥
ç sin ç 2 ÷ ÷
è ø ÷ d .
s 2 = 4 ò G0 ( ) ç
ç
÷
-¥
ç
÷
è
ø
82
83.
æ sin æ t ö öç çè 2 ÷ø ÷
h ( t ) = ç
÷
è
ø
2
tö
æ sin æ
ö
ç
÷
ç è 2 ø÷
lim ç
÷
®0 è
ø
2
tö
®
1
4
t
2
æ sin æ
ö
ç
÷
ç è 2 ø÷
lim ç
÷
t ®0 è
ø
2
®0
1
t=2
h( 2)
h( 1)
0.5
t=1
0
10
0
10
83
84. Вывод:
Даже если шум «на входе» h(t) стационарный,винеровский процесс (t) «на выходе»
t
(t ) = ò h (t )dt 0
нестационарный:
2
æ
æ t ö ö
¥
ç sin ç 2 ÷ ÷
è
ø
2
ç
÷ d
s (t ) = 4 ò G0 ( )
ç
÷
-¥
ç
÷
è
ø
84
85.
Предельный случай t ® 0t
s (t ) = 2 ò d (t - ) K 0 ( )
2
0
2
h (t )h (t + ) = Kпри
(
)
»
s
0
0
s = 2s 0
2
®0
t
t
2
ò d (t - ) = 2s
0
2
0
1 2ö
æ
2 2
ç t - ÷ = s 0 t ;
2 ø0
è
s = s 0t
85
86.
Конечное время корреляцииt
s 2 (t ) = 2 ò d (t - ) K 0 ( );
0
æ t
K 0 (t ) = s exp ç è 0
2
0
t
ö
÷,
ø
Символьное вычисление интеграла с помощью MathCad:
-
o
-t ö
2
2
æ
( t - ) e
d ® exp ç
+
t
o
o
o
÷
0
o
è ø
86
87.
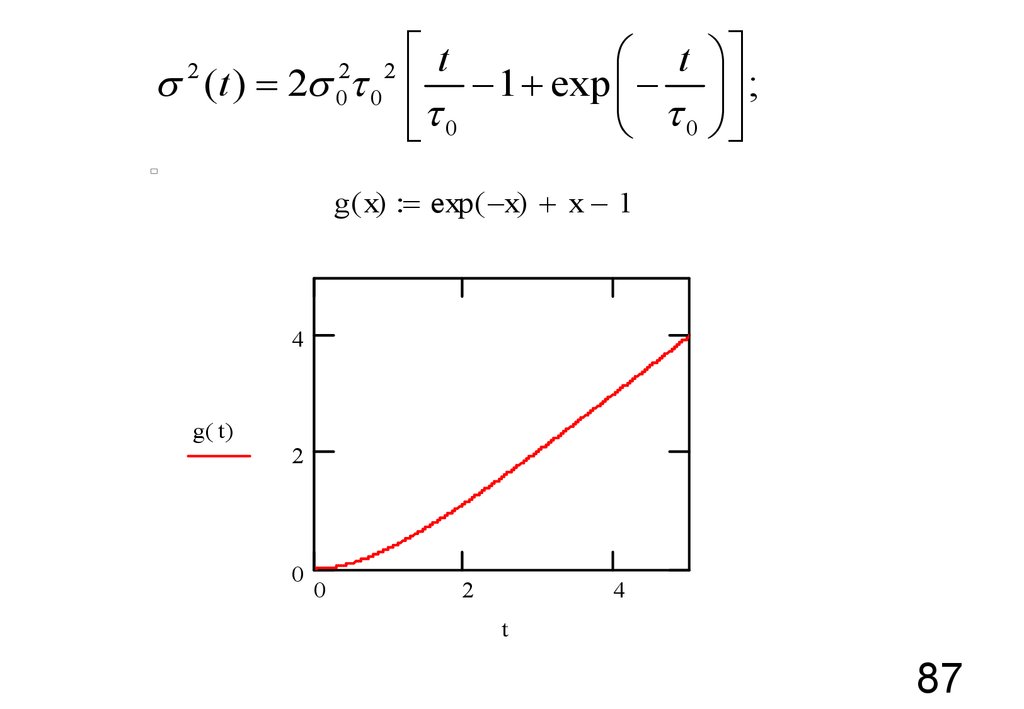
s (t ) = 2s2
2
2
0 0
ét
æ t
- 1 + exp ç è 0
ë 0
öù
÷ ;
øû
g ( x) = exp ( -x) + x - 1
4
g( t)
2
0
0
2
4
t
87
88.
Предельный случай t ® ¥s (t ) = 2s
2
2
2
0 0
ét
æ t
- 1 + exp ç è 0
ë 0
öù
÷ ;
øû
При t 0
é
ù
æ
ö
t
t
s 2 (t ) = 2s 02 0 2 - 1 + exp ç - ÷ » 2s 02 0 [ t - 0 ]
ë 0
è 0 ø û
s 2 (t ) » 2s 02 0 [ t - 0 ]
88
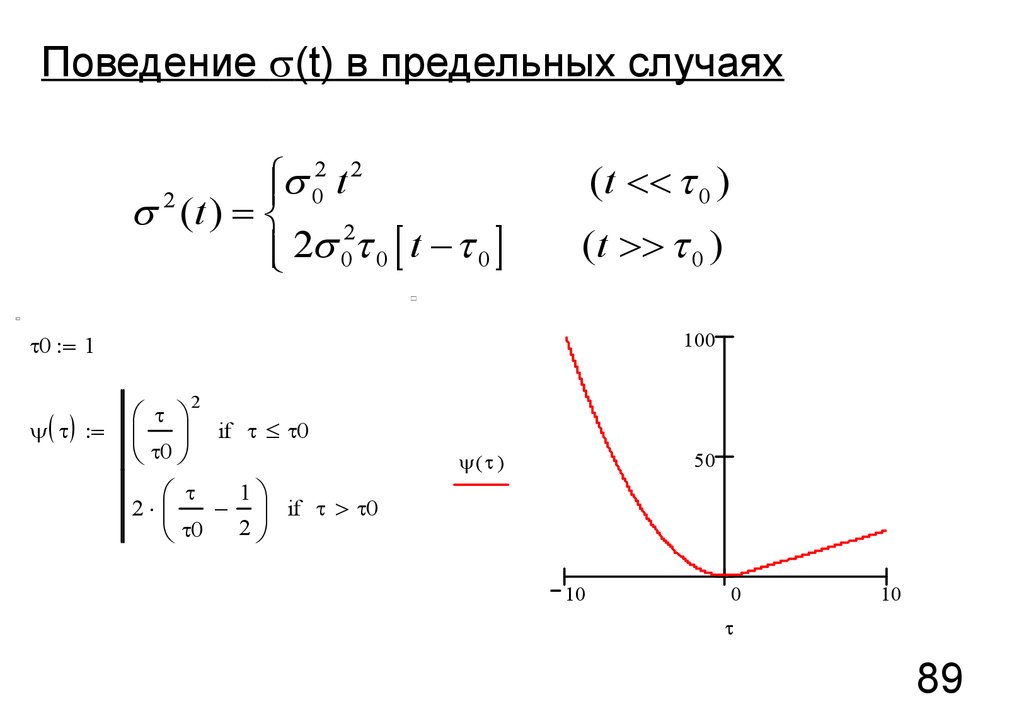
89.
Поведение s(t) в предельных случаях2 2
ì
s
ï 0t
2
s (t ) = í 2
ï
î 2s 0 0 [ t - 0 ]
(t << 0 )
(t 0 )
100
0 = 1
y ( ) =
2
æ ö if 0
ç ÷
è 0 ø
æ - 1 ö if 0
2 ç
÷
è 0 2 ø
y ( )
50
10
0
10
l = 2
= 5
89
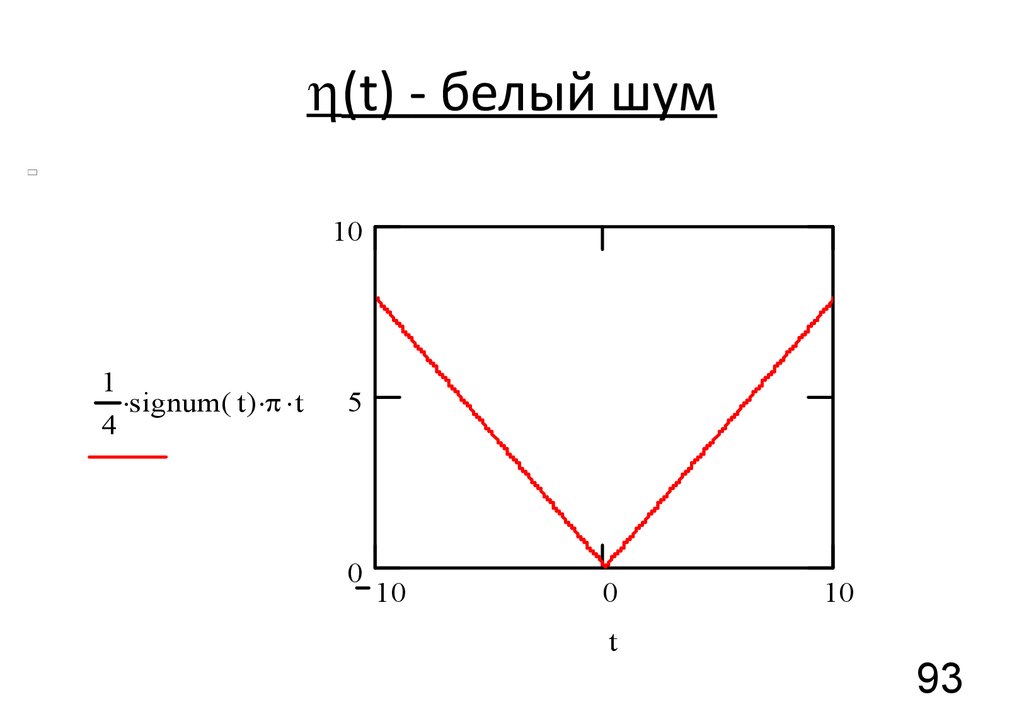
90. (t) - белый шум
h(t) - белый шумG0 ( ) = const = G0
интенсивность шума одинакова на всех частотах
h (t )h (t + ) = K 0 ( ) =
¥
i t
G
(
)
e
d =
ò 0
-¥
ì0, если t ¹ 0;
= G0 ò e d = G0 í
=
î¥, если t = 0.
-¥
= 2p G0d (t ).
¥
¥
òe
i t
i t
d = 2p d (t ).
-¥
K 0 ( ) = 2 D d (t ) ; D = p G0 .
90
91. (t) - белый шум
h(t) - белый шум1 - й способ
t
s = 2 ò d (t - ) K 0 ( )
2
0
t
t
0
0
s 2 = 2 ò d (t - )2 D d ( ) = 4 D ò d (t - ) d ( ) =
= 2 Dt.
s = 2 Dt
91
92. (t) - белый шум
h(t) - белый шум2 - й способ
2
æ
æ
æ t ö ö
æ t ö ö
¥
¥
ç sin ç 2 ÷ ÷
ç sin ç 2 ÷ ÷
è ø ÷ d = 4G d ç
è ø÷
s 2 (t ) = 4 ò G0 ( ) ç
0 ò
ç
÷
ç
÷
-¥
-¥
ç
÷
ç
÷
è
ø
è
ø
¥
- ¥
2
2
æ sin æ t ö ö
ç çè 2 ÷ø ÷
1
ç
÷ d ® signum( t) p t
2
è
ø
92
93. (t) - белый шум
h(t) - белый шум10
1
signum( t) p t
4
5
0
10
0
t
10
93
94. (t) - белый шум
h(t) - белый шум2
2
æ
æ
æ t ö ö
æ t ö ö
¥
¥
ç sin ç 2 ÷ ÷
ç sin ç 2 ÷ ÷
è ø ÷ d = 4G d ç
è ø÷ =
s 2 (t ) = 4 ò G0 ( ) ç
0 ò
ç
÷
ç
÷
-¥
-¥
ç
÷
ç
÷
è
ø
è
ø
= 2 D t (t ³ 0), D = p G0
Таким образом
s 2 (t ) = 2 D t
94
95. (t) - белый шум
h(t) - белый шумДля этого частного случая можно также вычислить
корреляционную функцию (без вывода) и коэффициент
корреляции
( ³ 0),
ì 2 Dt
ï
K (t , ) = (t ) (t + ) = í2 D(t - )
( -t < 0),
ï0
( < -t.
î
1
ì
ï 1+ / t
ï
ï t-
K (t , )
R (t , ) =
=í
s (t )s (t + )) ï 1 + / t
ï0
ï
î
( ³ 0),
( -t < 0),
( < -t.
95
96. (t) - белый шум
h(t) - белый шумR( )
=
1
1+
1-
1
1+
if ³ 0
if -1 < 0
0 otherwise
R( )
0.5
0
10
20
30
40
50
96
97. Гауссовский спектр мощности
G0 ( ) = G0 (0) exp(- / 2h ).2
2
При этом
K 0 ( ) = s exp(-h / 2);
2
0
2
2
s = 2p G0 (0)h
2
0
Используем формулу
2
æ
æ t ö ö
¥
ç sin ç 2 ÷ ÷
è ø ÷ d
s 2 (t ) = 4 ò G0 ( ) ç
ç
÷
-¥
ç
÷
è
ø
97
98. Гауссовский спектр мощности Используем численный расчет. Обозначено: s(t)=2(t)
Гауссовский спектр мощностиИспользуем численный расчет. Обозначено: s(t)=s2(t)
¥
1
2
é
s ( t ) =
exp - ( ) ù
ë 2
û
- ¥
tö
2
æ sin æ
ö
ç çè 2 ÷ø ÷
ç
÷ d
è
ø
4
s( t )
2
0
0
2
t
4
98
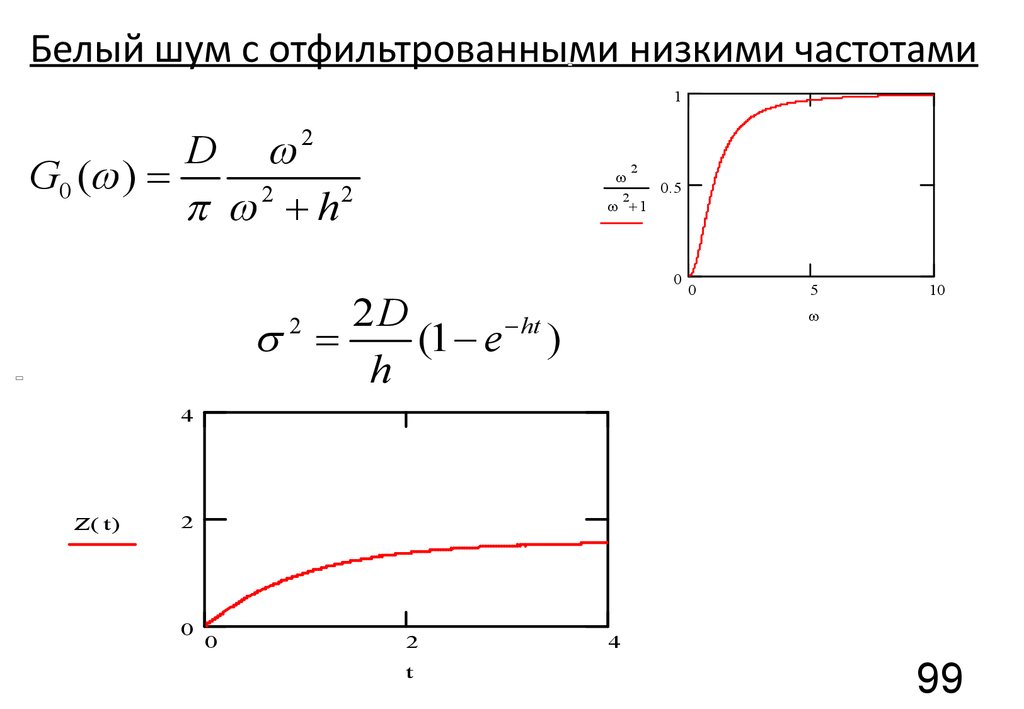
99. Белый шум с отфильтрованными низкими частотами
1D
G0 ( ) =
p 2 + h2
2
2
2
+1
0.5
0
2D
s =
(1 - e - ht )
h
0
5
10
2
4
Z( t )
2
0
0
2
t
4
99
100. Фликкер-шум (шум 1 /f) Спектр мощности имеет вид:
Фликкер-шум (шум 1 /f )Спектр мощности имеет вид:
G0 ( ) =
D 0
p
,
0 1.
10
1
5
0
0
5
10
1
Принимая = , произведем расчет s (t )
2
100
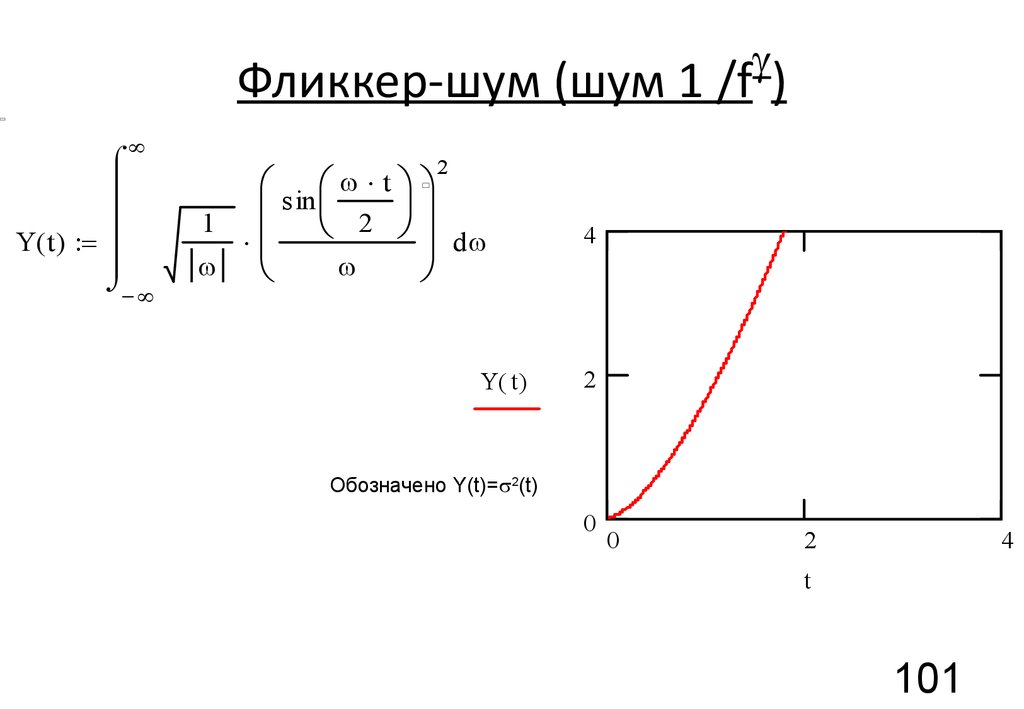
101. Фликкер-шум (шум 1 /f)
Фликкер-шум (шум 1 /f )¥
Y( t ) =
- ¥
tö
2
æ sin æ
ö
ç
÷
ç è 2 ø÷
1
ç
÷ d
è
ø
Y( t)
4
2
Обозначено Y(t)=s2(t)
0
0
2
4
t
101
102. Фликкер-шум (шум 1 /f)
Фликкер-шум (шум 1 /f )2D
t +
s =
( 0t )
0 cos p / 2
2
102
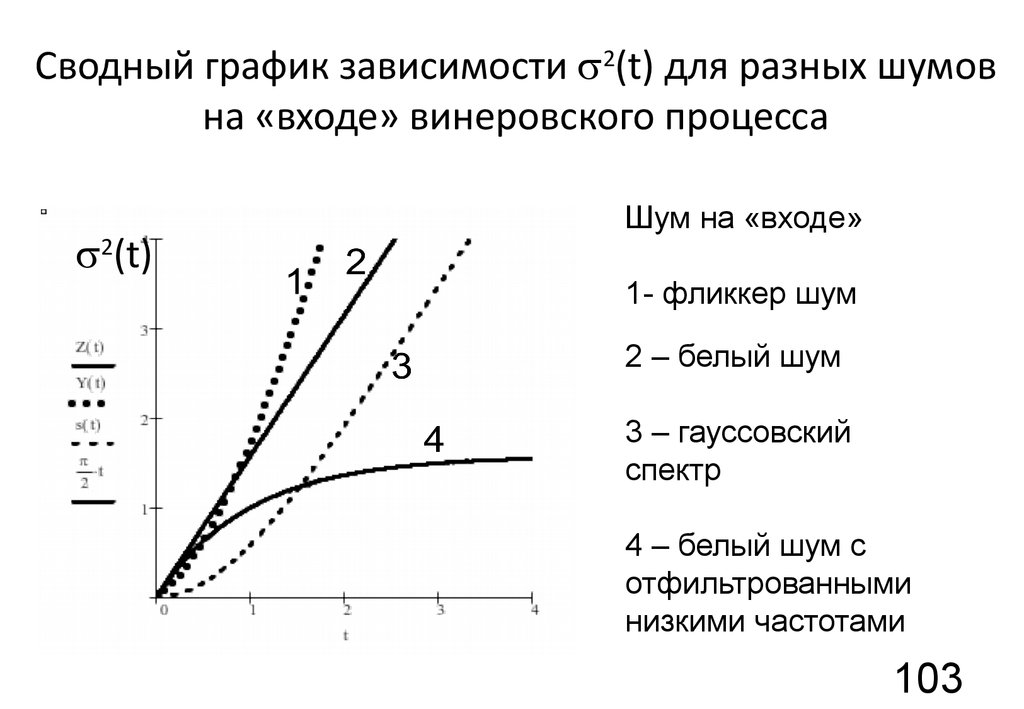
103. Сводный график зависимости 2(t) для разных шумов на «входе» винеровского процесса
Сводный график зависимости s2(t) для разных шумовна «входе» винеровского процесса
s2(t)
Шум на «входе»
1- фликкер шум
2 – белый шум
3 – гауссовский
спектр
4 – белый шум с
отфильтрованными
низкими частотами
103
104.
Модели случайных процессов (план) см [1]. Глава 2Спектральный анализ сигналов
Гауссовский случайный процесс
Узкополосный стационарный шум
Узкополосный гауссовский шум
• Узкополосный негауссовский шум (ознакомиться
самостоятельно!)
Диффузионный (винеровский) процесс
• Колебания, модулированные шумом
- амплитудная модуляция
- фазовая модуляция
- частотная модуляция
• Импульсные случайные процессы
104
105. Колебания, модулированные шумом. Амплитудная модуляция (АМ) шумом
h (t )A (t ) = a0 [ 1 + h (t ) ] cos( 0t + j0 )
Amplitude - амплитуда
Постановка задачи:
Задан шум
h (t )
(t ) = ?
Постановка задачи обратная по
сравнению с той, которая была для
узкополосного шума
105
106. Колебания, модулированные шумом. Фазовая модуляция (ФМ) шумом
h (t )P (t ) = a0 cos( 0t + h (t ))
Phase – фаза
Постановка задачи:
Задан шум
h (t )
(t ) = ?
Постановка задачи обратная по
сравнению с той, которая была для
узкополосного шума
106
107. Колебания, модулированные шумом. Частотная модуляция (ЧМ) шумом
h (t )(
t
F (t ) = a0 cos 0t + ò h (t ) dt
0
)
Frequency - частота
Постановка задачи:
Задан шум
h (t )
Постановка задачи обратная по сравнению с
той, которая была для узкополосного шума
(t ) = ?
107
108.
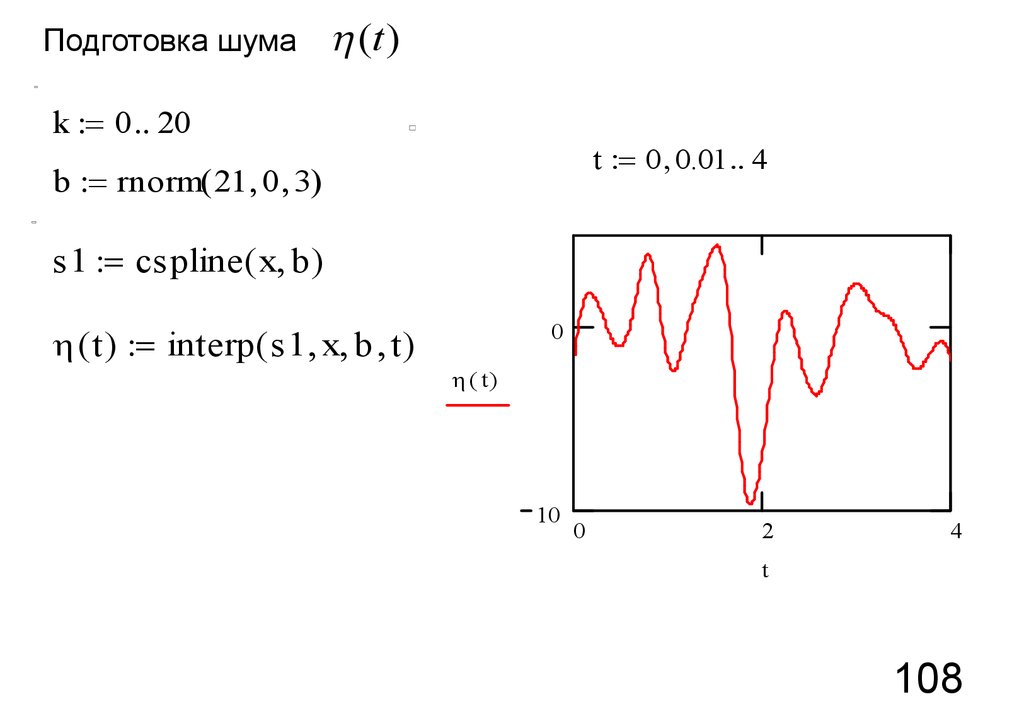
Подготовка шумаh (t )
k = 0 20
t = 0 0.01 4
b = rnorm( 21 0 3)
s1 = cspline( x b )
0
h ( t ) = interp ( s1 x b t )
h ( t)
10
0
2
4
t
108
109.
Амплитудная модуляция шумомA ( t ) = ( 1 + 0.1 h ( t ) ) cos ( 20t )
2
A( t)
0
1
2
3
4
2
t
109
110.
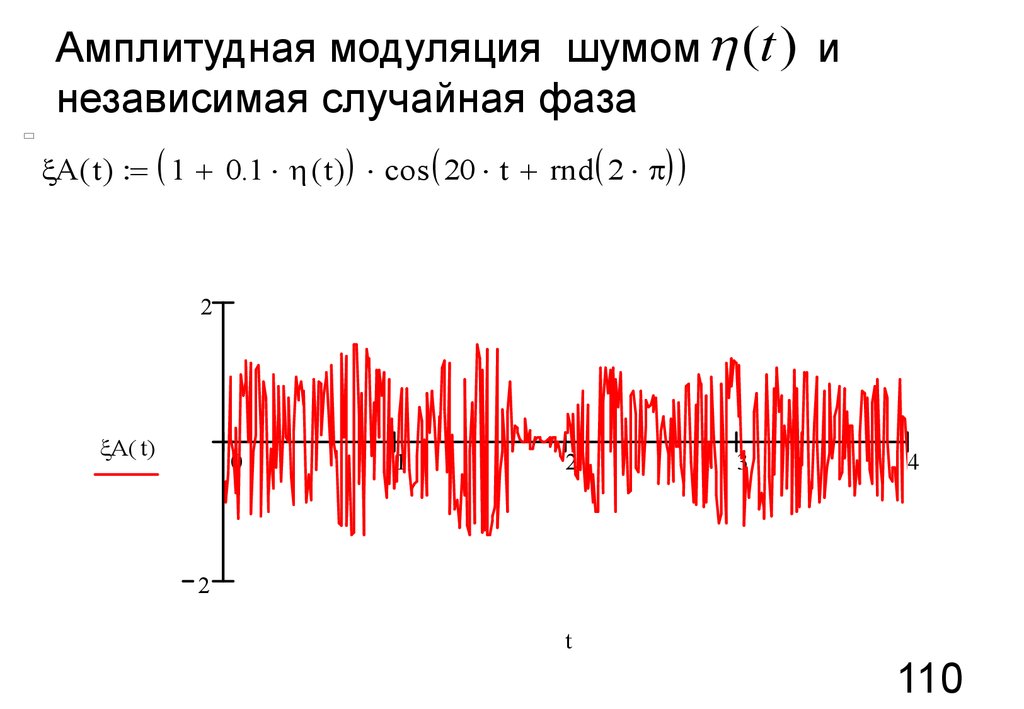
Амплитудная модуляция шумом h (t ) инезависимая случайная фаза
A ( t ) = ( 1 + 0.1 h ( t ) ) cos ( 20 t + rnd ( 2 p) )
2
A( t)
0
1
2
3
4
2
t
110
111.
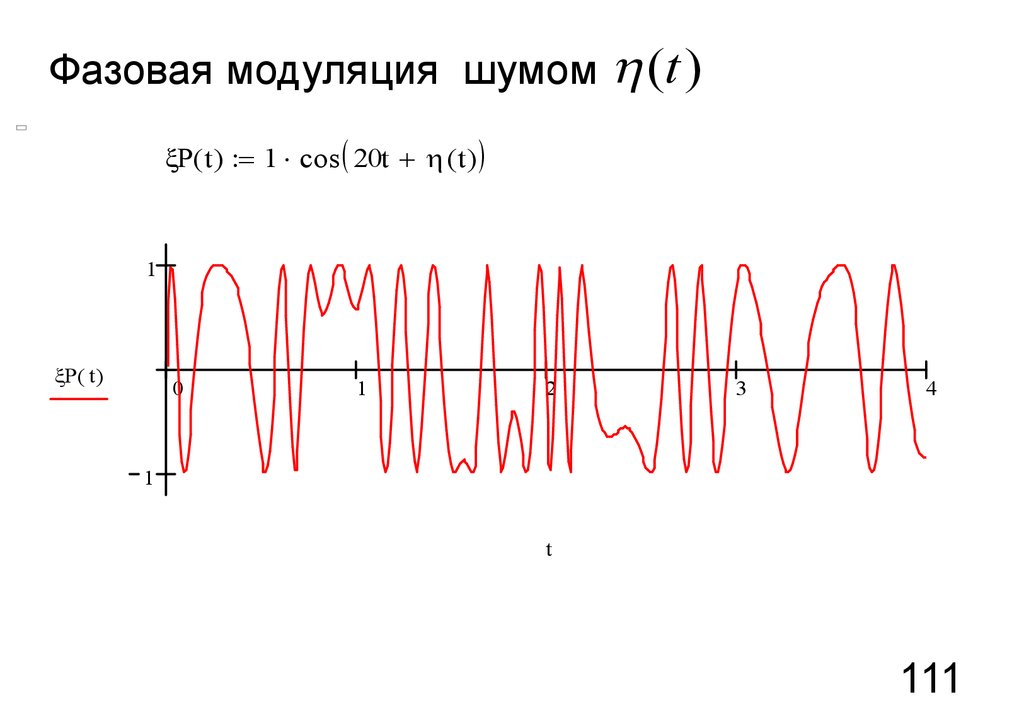
Фазовая модуляция шумом h (t )P( t) = 1 cos ( 20t + h ( t ) )
1
P ( t)
0
1
2
3
4
1
t
111
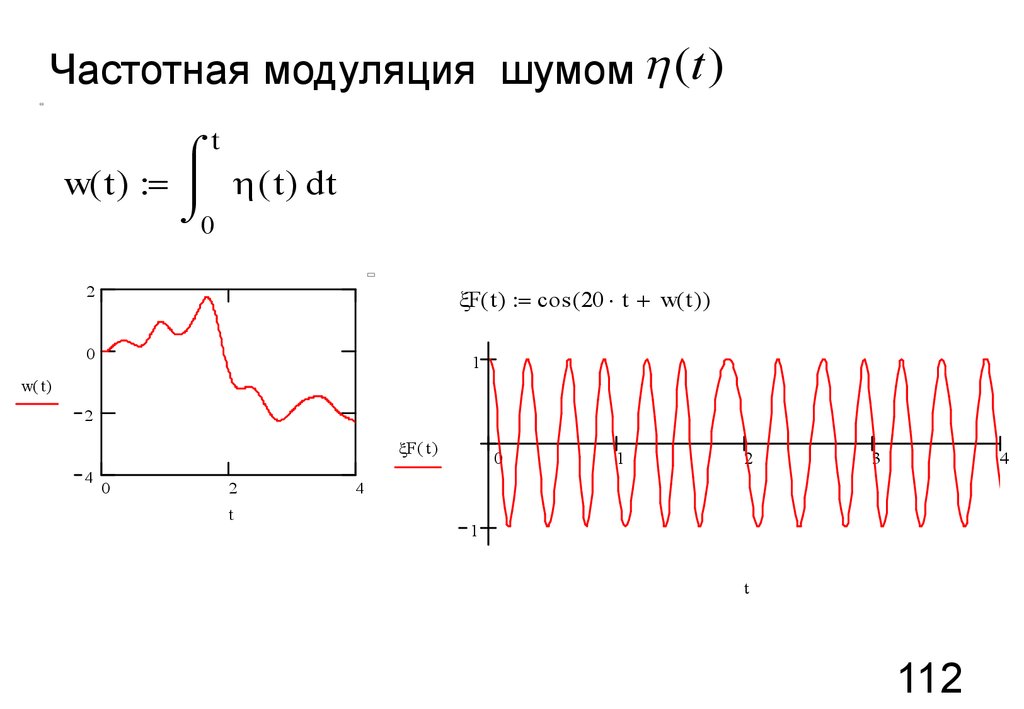
112.
Частотная модуляция шумом h (t )t
w( t ) = h ( t ) d t
0
2
F( t) = cos ( 20 t + w( t ) )
0
1
w( t)
2
F ( t)
4
0
2
t
0
1
2
3
4
4
1
t
112
113.
Амплитудная модуляция (АМ) подробноh (tстационарный
)случайный процесс
j0 - равномерно распределена на интервале [ 0, 2p ]
1
w(j0 ) =
;
2p
h = 0;
hh = K 0 ( ) =
¥
- i t
G
(
)
e
d .
ò 0
-¥
Найдем среднее от
(t ) = a0 éë1 + h (t ) ùû cos( 0t + j0 )
h (t ) = 0;
1
cos( 0t + j0 ) =
2p
(t ) = 0
2p
ò cos( t + j
0
0
) dj 0 = 0
0
113
114. Ищем корреляционную функцию процесса
Амплитудная модуляция (АМ)Ищем корреляционную функцию процесса
K (t ) = =
= ( a0 ) [ 1 + h (t ) ] cos( 0t + j0 ) [ 1 + h (t + ) ] cos( 0 (t + ) + j0 ) =
2
2
= ( a0 ) é1 + h (t ) + h (t + ) + h (t )h (t + ) ù cos( 0t + j0 ) cos( 0 (t + ) + j0 ) =
ë
û
= ( a0 ) [ 1 + K 0 ( ) ] cos( 0t + j0 ) cos( 0 (t + ) + j0 );
2
Здесь подразумевается усреднение по
случайной фазе 0:
1
f(j0 ) =
2p
2p
ò f(j0 )dj0
0
114
115.
Амплитудная модуляция (АМ)cos( 0t + j0 ) cos( 0 (t + ) + j 0 ) =
= ( cos 0t cos j0 - sin 0t sin j 0 ) ( cos 0 (t + ) cos j0 - sin 0 (t + ) sin j0 ) .
1
1
; sin 2 j 0 = ; cos j0 sin j0 = 0.
2
2
cos( 0t + j0 ) cos( 0 (t + ) + j 0 ) =
cos 2 j0 =
1
( cos 0t cos 0 (t + ) + sin 0t sin 0 (t + ) ) =
2
1
1
= cos( 0t - 0t - 0 ) = cos( 0 )
2
2
K ( ) = =
=
= ( a0 ) [ 1 + K 0 ( ) ] cos( 0t + j0 ) cos( 0 (t + ) + j0 ) =
2
1
2
= ( a0 ) [ 1 + K 0 ( ) ] cos( 0 ).
2
1
2
K ( ) = ( a0 ) [ 1 + K 0 ( ) ] cos( 0 ).
2
115
116.
Амплитудная модуляция (АМ)Перейдем к вычислению спектральной плотности процесса (t)
1
G ( ) =
2p
1
2
=
a
( 0)
4p
1
2
=
a
( 0)
4p
¥
¥
ò
K ( )e - i d =
-¥
¥
ò [ 1 + K 0 ( )]
cos( 0 )e - i d =
-¥
¥
- i
cos(
)
+
K
(
)
cos(
)
e
d .
[
]
0
0
0
ò
-¥
(1)
(2)
¥
1
i 0
- i 0
- i
- i
cos(
)
e
d
=
(
e
+
e
)
e
d =
(1) ò
0
ò
2 -¥
-¥
= p ( d ( 0 - ) + d ( 0 + ) ) .
¥
ò
-¥
eib x d xиспользованная
= 2pd ( b ) ¬
фор
мула
116
117.
Амплитудная модуляция (АМ)¥
(2)
ò
K 0 ( ) cos( 0 ) e - i d =
-¥
¥
1
= ò K 0 ( ) (ei 0 + e - i 0 ) e - i d =
2 -¥
¥
1
i ( 0 - )
- i ( 0 + )
= ò K 0 ( ) (e
+e
) d =
2 -¥
= p ( G0 ( 0 - ) + G0 ( 0 + ) ) .
117
118.
Амплитудная модуляция (АМ)1
2
G ( ) = ( a0 ) [ d ( 0 - ) + d ( 0 + ) + G0 ( 0 - ) + G0 ( 0 + ) ]
4
Исходный
спектр
мощности
шума
Спектр
мощности
амплитудно
модулированного шумом
сигнала
118
119. Колебания, модулированные шумом Фазовая модуляция (ФМ) гауссовским шумом
x(t ) = a0 cos [ 0t + j (t ) ]1
x(t ) = a0 exp éëi ( 0t + j (tк) )сùû + . .
2
1
a0 exp éë -i ( 0t + j (t ) ) ùû
2
Предположим, что j (t ) - стационарный гауссовский
процесс.
j (t ) = 0;
j (t )j (t + ) = K 0 ( ) = s 02 R0 ( );
K 0 ( ) =
¥
ò
G0 ( )e - i d ;
-¥
w(j ) =
ì j2 ü
1
exp í.
2 ý
2p s 0
î 2s 0 þ
119
120. Фазовая модуляция (ФМ) гауссовским шумом Задача состоит в том, чтобы найти статистические характеристики сигнала x(t)
1i[ 0t +j ( t )]
x(t ) = a0 eк с
+ ..
2
1
1
i[ 0t +j ( t )]
x(t ) = a0 e
+ ... = a0 ei 0t eij (t ) .
2
2
¥
¥
2
ì
1
j ü
ijt
ij ( t )
ij
e
= ò e w(jt )djt = ò e
exp ídj =
2 ý
2p s 0
î 2s 0 þ
-¥
-¥
=
1
2p s 0
eij (t ) = e
¥
ì j2
ü
ì s 02 ü
ò-¥ dj exp íî- 2s 02 + ij ýþ = exp íî- 2 ýþ .
s 02
2
120
121.
eij ( t ) = e-
s0
2
Фазовая модуляция (ФМ)
2
1
x(t ) = a0 éëei 0t eij (t ) + e - i 0t e - ij (t ) ùû =
2
1
= a0 e
2
s 02
2
cos 0t.
Для усреднения функции двух переменных j(t) и j(t+ ) также
используем распределение Гаусса (для двух переменных).
e
ij ( t )
e
± ij ( t + )
=e
s 02
[ 1± R0 ( )]
2
2
a0 é
- 2s 0 2
s =x =
1+ e
cos 2 0t ù .
û
2 ë
2
2
121
122. Введем флуктуационную компоненту фазово-модулированного сигнала:
Фазовая модуляция (ФМ)Введем флуктуационную компоненту фазовомодулированного сигнала:
(t ) = x(t ) - x(t )
и для неё вычислим корреляционную функцию
K (t , ) = =
2
a0
=
e
2
s 02
2
éë e K0 ( ) - 1ùû [ cos 0 - cos 2( 0 + 0t ) ] .
Таким образом, фазово-модулированный сигнал
оказывается нестационарным случайным процессом.
122
123.
Фазовая модуляция (ФМ)Зависимость от времени периодическая. Проведем также усреднение всех
величин по периоду колебаний (по времени), так как именно такие величины
регистрируются приборами.
1
f (t ) =
T
T
ò f (t )dt
0
T
1
K (t , ) = ò K (t , ) dt =
T 0
2
a0
=
e
2
2
a0
=
e
2
s 02
2
s 02
2
éë e K0 ( )
1
- 1ùû
T
T
ò [ cos - cos 2( + t )] dt =
0
0
0
0
éë e K0 ( ) - 1ùû cos 0 .
2
a0
K (t , ) =
e
2
s 02
2
éëe K0 ( ) - 1ùû cos 0 .
123
124.
1G ( ) =
2p
¥
ò
Фазовая модуляция (ФМ)
K ( ) e - i d .
-¥
2
a0
K (t , ) =
e
2
s 02
2
2
1 a0
G ( ) =
e
2p 2
=
¥
1
2
a
( 0) e
4p
éëe K0 ( ) - 1ùû cos 0
s 02 ¥
2
ò
-¥
s 02 ¥
2
ò
-¥
éëe K0 ( ) - 1ùû cos 0 e - i d .
ée K0 ( ) cos( 0 ) - cos( 0 ) ù e - i d .
ë
û
¥
1
i 0
- i 0
- i
- i
cos(
)
e
d
=
(
e
+
e
)
e
d =
0
ò-¥
ò
2 -¥
= p ( d ( 0 - ) + d ( 0 + ) ) .
¥
ò
-¥
eib x d xиспользованная
= 2pd ( b ) ¬
формула
124
125.
Фазовая модуляция (ФМ)Мы видим, что спектр состоит из непрерывной компоненты и
двух дискретных
1
2
G ( ) =
( a0 ) e
4p
s 02
2
¥
ì
ü
é
ù
ï
ï
K 0 ( ) - i
e
e
cos(
)
d
p
d
(
)
+
d
(
+
)
é
ù
(
)
í ò
ë
0
0
0
ûý
ï
ï
û
î ë -¥ Непрерывная
þ
Дискретные компоненты
компонента
Введем интегральную интенсивность спектра
¥
I=
ò d G ( ) = I
нeпрер
- I дискр .
-¥
125
126.
I дискр1
2
=
( a0 ) e
4p
1
2
= ( a0 ) e
2
I непрер
s 02 ¥
2
ò d p ( d (
- ) + d ( 0 + ) ) =
-¥
s 02
2
.
1
2
=
( a0 ) e
4p
s 02 ¥
2
1
2
=
( a0 ) e
4p
s 02
2
1
2
= ( a0 ) e
2
0
ò
-¥
s 02
2
s 02
2
d
2p
¥
ò
e K0 ( ) e - i cos( 0 ) d =
-¥
¥
ò
e K0 ( )d ( ) cos( 0 ) d =
-¥
e K0 (0) =
1
2
= ( a0 ) eУчтено
.
что, K
2
2
(0)
=
s
0
0 .
126
127.
I = I непрер - I дискр =1
2æ
= ( a0 ) ç e
ç
2
è
s 02
2
-e
s 02
2
ö
÷.
÷
ø
При слабой модуляции сигнала:
2
1 a0
G ( ) =
e
2p 2
2
a0
»
e
4p
-
s 02 ¥
2
ò
-¥
s 02 ¥
2
ò
K 0 ( ) << s 0 2 << 1
éëe K0 ( ) - 1ùû cos 0 e - i d »
K 0 ( ) cos 0 e - i d =
-¥
a0 2
=
[ G0 ( - 0 ) + G0 ( + 0 )]
4
127
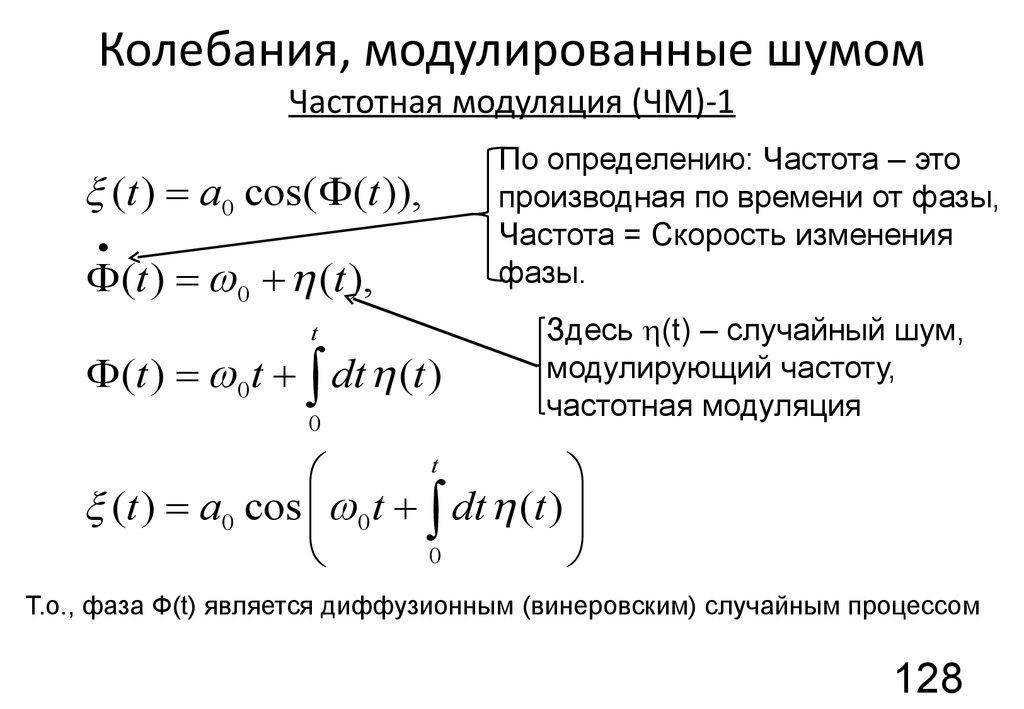
128. Колебания, модулированные шумом Частотная модуляция (ЧМ)-1
(t ) = a0 cos(F (t )),·
F (t ) = 0 + h (t ),
t
F (t ) = 0t + ò dt h (t )
0
По определению: Частота – это
производная по времени от фазы,
Частота = Скорость изменения
фазы.
Здесь h(t) – случайный шум,
модулирующий частоту,
частотная модуляция
t
æ
ö
(t ) = a0 cos ç 0t + ò dt h (t ) ÷
0
è
ø
Т.о., фаза Ф(t) является диффузионным (винеровским) случайным процессом
128
129. Частотная модуляция (ЧМ)-2
Зададим свойства шума h(t):1) шум считаем стационарным;
2
2
h
=
0;
h
=
s
2)
0;
hh = K 0 ( ) =
¥
ò
G0 ( ) e -i t d .
-¥
Наша задача: исследовать статистические свойства
t
1) фазы
j (t ) = ò dt h (t );
0
2) самого колебания (t).
129
130. Частотная модуляция (ЧМ)-3
Как мы знаем из свойств диффузионного процесса (см. выше,формула ) при любой статистике шума h(t)
t
j 2 = s 2 (t ) = 2 ò d (t - ) K 0 ( ).
0
При t ® ¥ приближенно имеем :
s 2 (t ) » 2 Dt ;
D = p G0 (0).
j изменяется на ограниченном интервале : 0 j 2p ,
поэтому в пределе t ® ¥
1
w(j ) »
, (0 j 2p ).
2p
130
131.
Частотная модуляция (ЧМ)-4В дальнейшем считаем шум h(t) гауссовским.
Используя полученные выше результаты для фазовой модуляции
колебаний, для корреляционной функции K( ) процесса (t) может
быть получено выражение (см. [Ахманов], стр. 165-166, а также
см. выше слайд 370):
a0 2 - s 02y ( )
K ( ) =
e
cos 0 ,
2
ì 2
,
ï
ï2
где y ( ) = í
ï D ( - 0 ) ,
2
ï
s
î 0
<< 0 ,
0 .
131
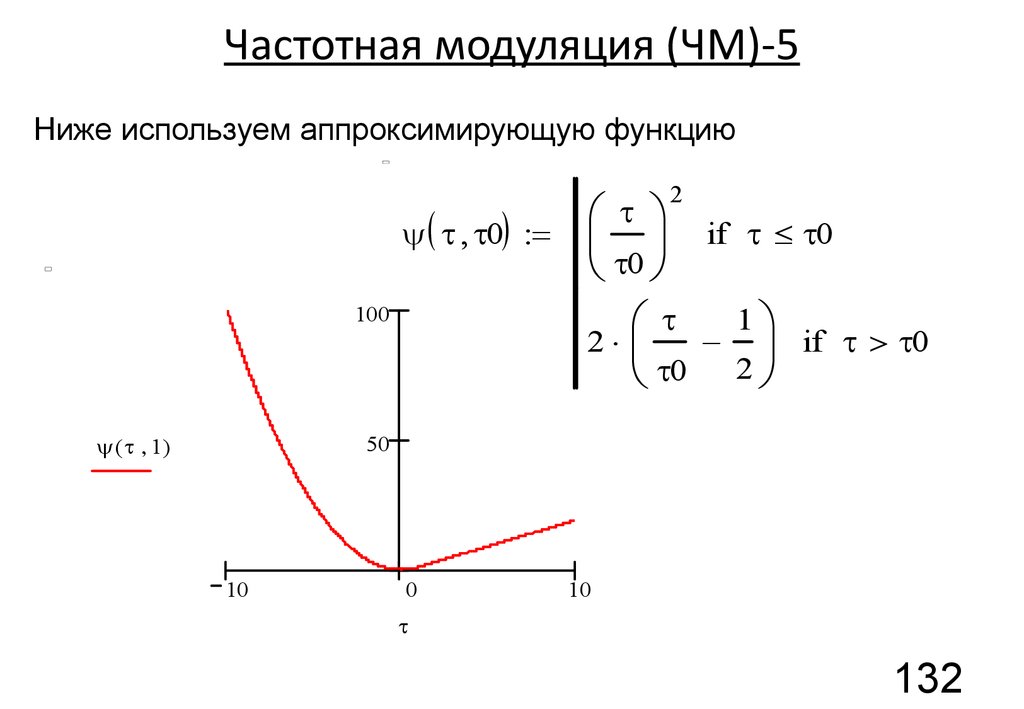
132.
Частотная модуляция (ЧМ)-5Ниже используем аппроксимирующую функцию
2
ö
æ
y ( 0) = ç ÷ if 0
è 0 ø
100
1ö
æ
2 ç
- ÷ if 0
è 0 2 ø
y ( 1)
50
10
0
10
= 3
132
133.
Частотная модуляция (ЧМ)-6Приближенная функция модулированного сигнала
K( l 0) = exp ( -l y ( 1) ) cos ( 0 )
Параметр l - это мера интенсивности модулирующего шума. Чем он
больше, тем больше интенсивность шума. Частота 0 – это основная
частота модулируемых колебаний
Слева проявляется
квадратичная
зависимость y от
2
Справа проявляется
линейная зависимость
y от
K( 0.01 2)
1
K( 5 5)
10
0
10
133
134.
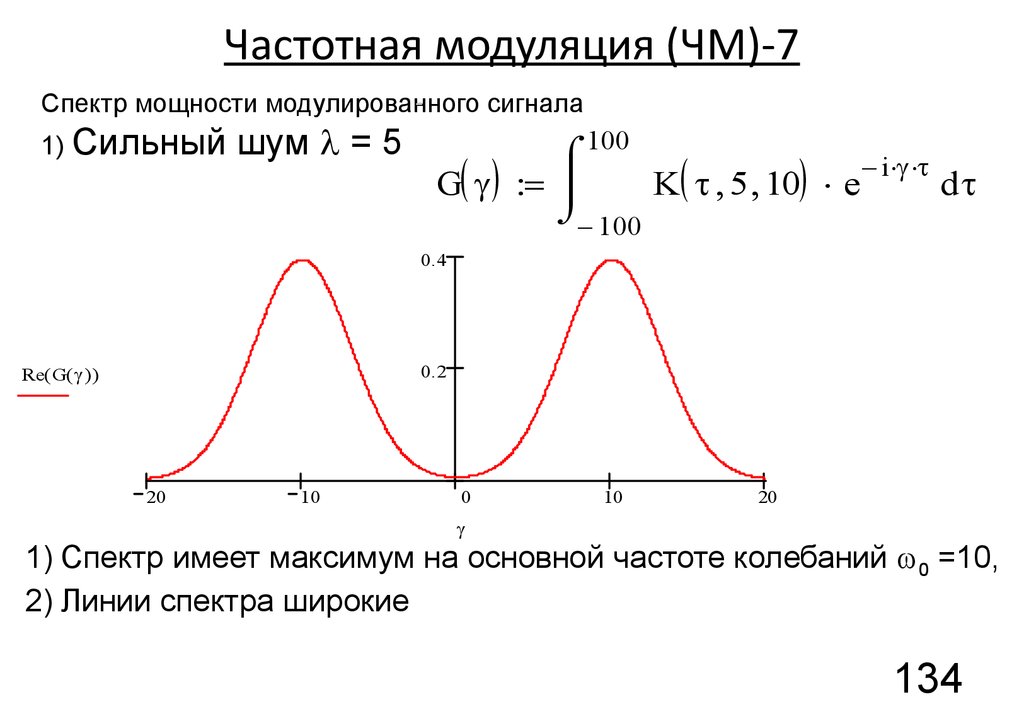
Частотная модуляция (ЧМ)-7Спектр мощности модулированного сигнала
1) Сильный
шум l = 5
100
- i
(
)
(
)
G =
K 5 10 e
d
- 100
0.4
0.2
Re( G( ) )
20
10
0
10
20
1) Спектр имеет максимум на основной частоте колебаний 0 =10,
2) Линии спектра широкие
134
135.
Частотная модуляция (ЧМ)-8Спектр мощности модулированного сигнала
2) Слабый
шум l = 0.01
100
- i
G( ) =
K( 0.01 10) e
d
- 100
5
Re( G( ) )
20
10
0
10
20
1) Спектр имеет максимум на основной частоте колебаний 0 =10,
2) Линии спектра очень узкие, что объясняется очень малой амплитудой
модуляции частоты.
135
136.
Частотная модуляция (ЧМ)-9Спектр мощности модулированного сигнала
3) Слабый
шум l = 0.1
100
- i
G( ) =
K( 0.1 10) e
d
- 100
5
Re( G( ) )
20
10
0
10
20
Линии спектра уширяются по мере нарастания амплитуды шума
136
137.
Частотная модуляция (ЧМ)-10Интерпретация полученных результатов
a0 2 - s 02y ( )
K ( ) =
e
cos 0 ,
2
s 0 2 0 2 1
1) При большой интенсивности модуляций
в корреляционной функции заменим y( ) на квадратичную
функцию 2 и получим гауссовский спектр ~ s 0
2
2
2
2
2
a0
(
)
/
2
s
(
+
)
/
2
s
0
0
0
0 ù
ée
G ( ) =
+e
û
4 2ps 0 ë
2) При малой интенсивности модуляций D 0 1
в корреляционной функции заменим y( ) на линейную функцию
~ D
и получим лоренцевский спектр
ù
a0 2 D é
1
1
G ( ) =
+ 2
2
2
4 p ë D + ( - 0 )
D + ( + 0 ) 2 û
137


![Модели случайных процессов (план) см [1]. Глава 2 Модели случайных процессов (план) см [1]. Глава 2](https://cf.ppt-online.org/files/slide/0/0a6UcFZEN8vBYKSTg5VdRsyX41nwWLO2r3uhGP/slide-2.jpg)





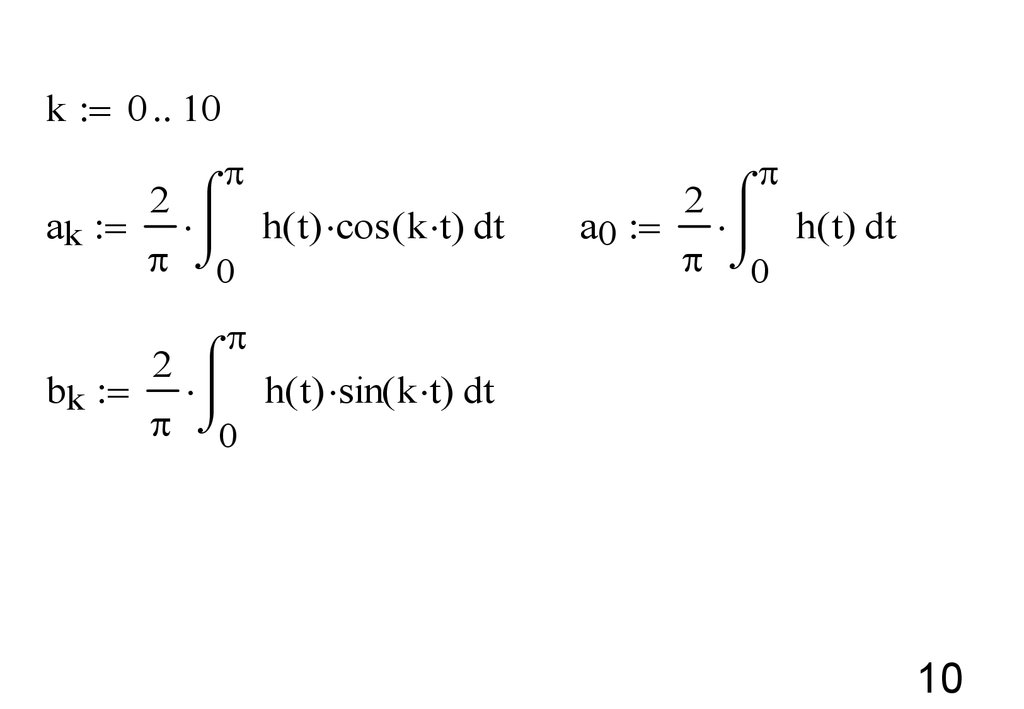

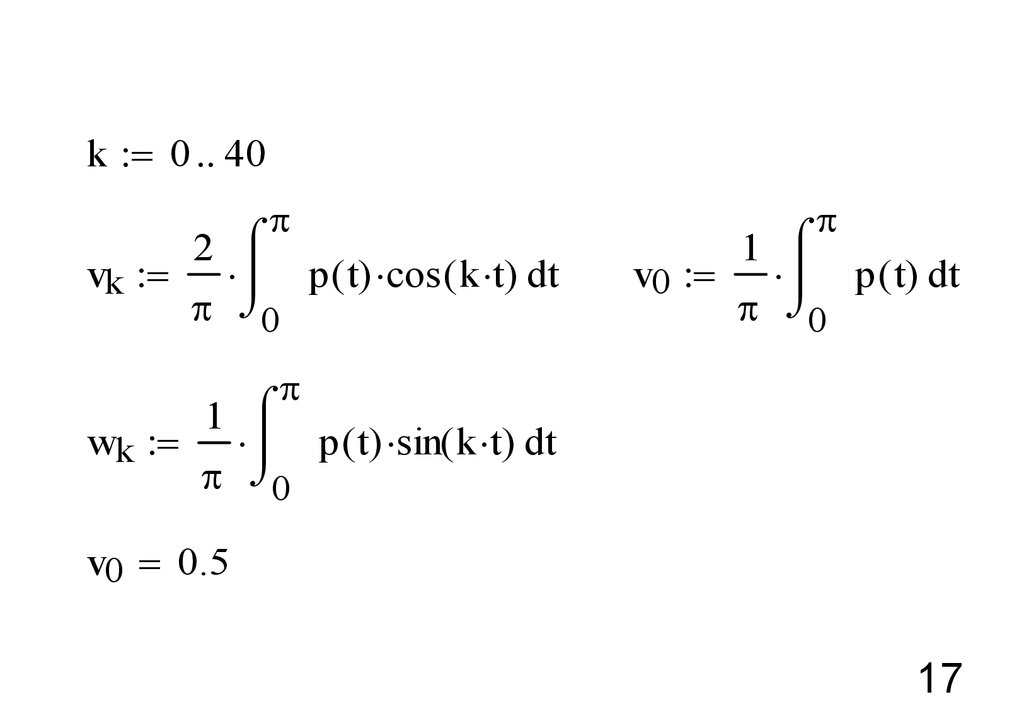
![Модели случайных процессов (план) см [1]. Глава 2 Модели случайных процессов (план) см [1]. Глава 2](https://cf.ppt-online.org/files/slide/0/0a6UcFZEN8vBYKSTg5VdRsyX41nwWLO2r3uhGP/slide-22.jpg)











![Модели случайных процессов (план) см [1]. Глава 2 Модели случайных процессов (план) см [1]. Глава 2](https://cf.ppt-online.org/files/slide/0/0a6UcFZEN8vBYKSTg5VdRsyX41nwWLO2r3uhGP/slide-37.jpg)










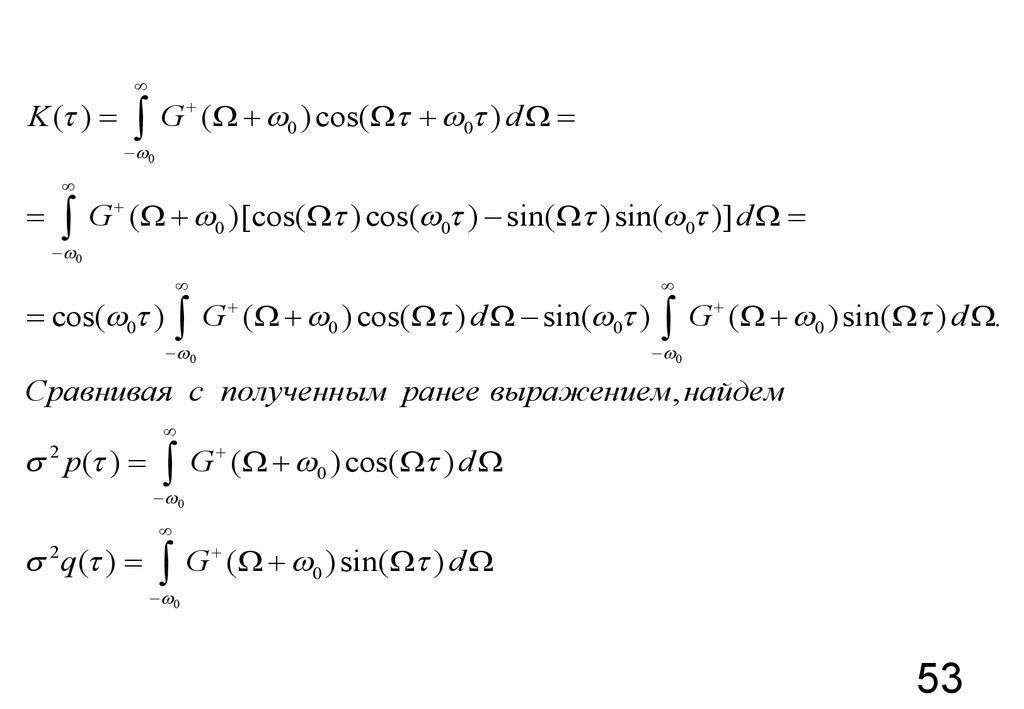

![Модели случайных процессов (план) см [1]. Глава 2 Модели случайных процессов (план) см [1]. Глава 2](https://cf.ppt-online.org/files/slide/0/0a6UcFZEN8vBYKSTg5VdRsyX41nwWLO2r3uhGP/slide-55.jpg)





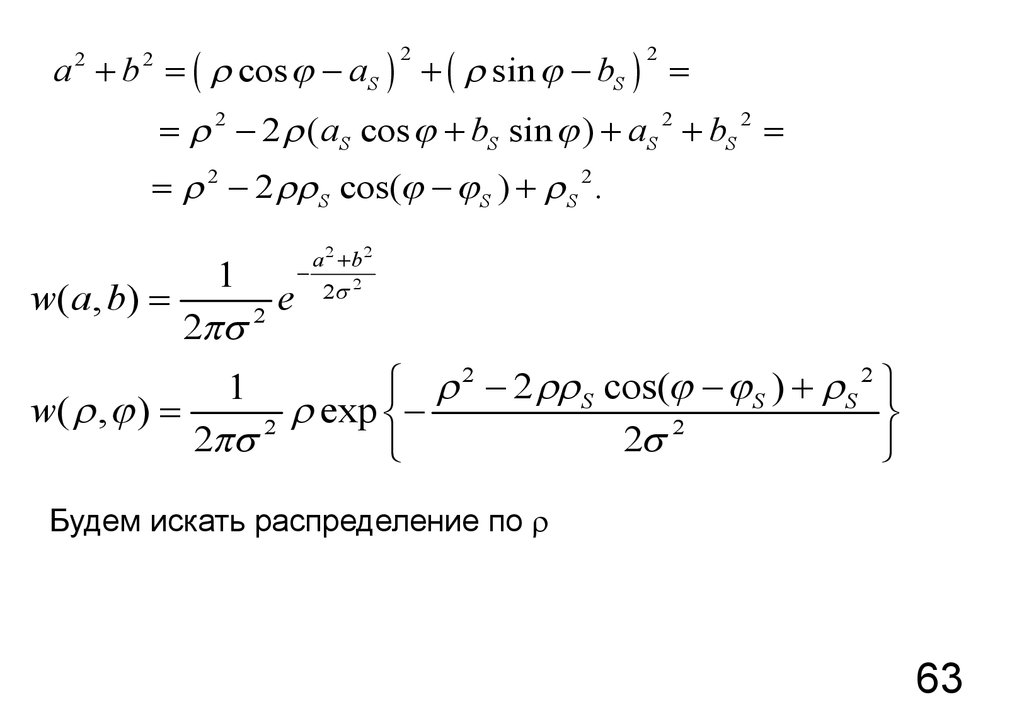





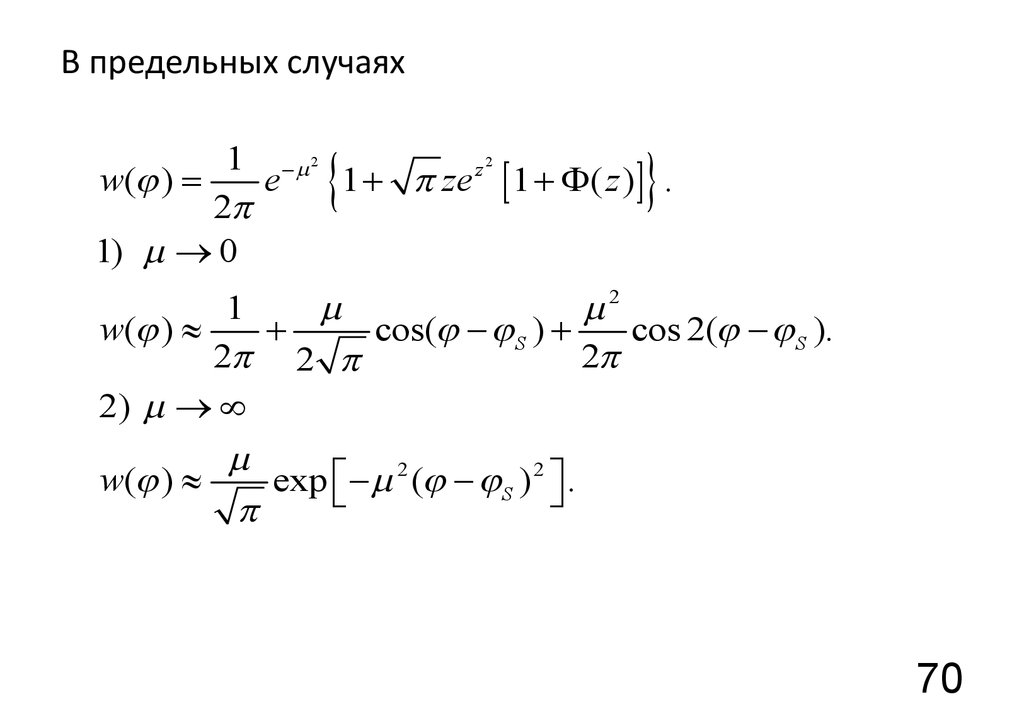


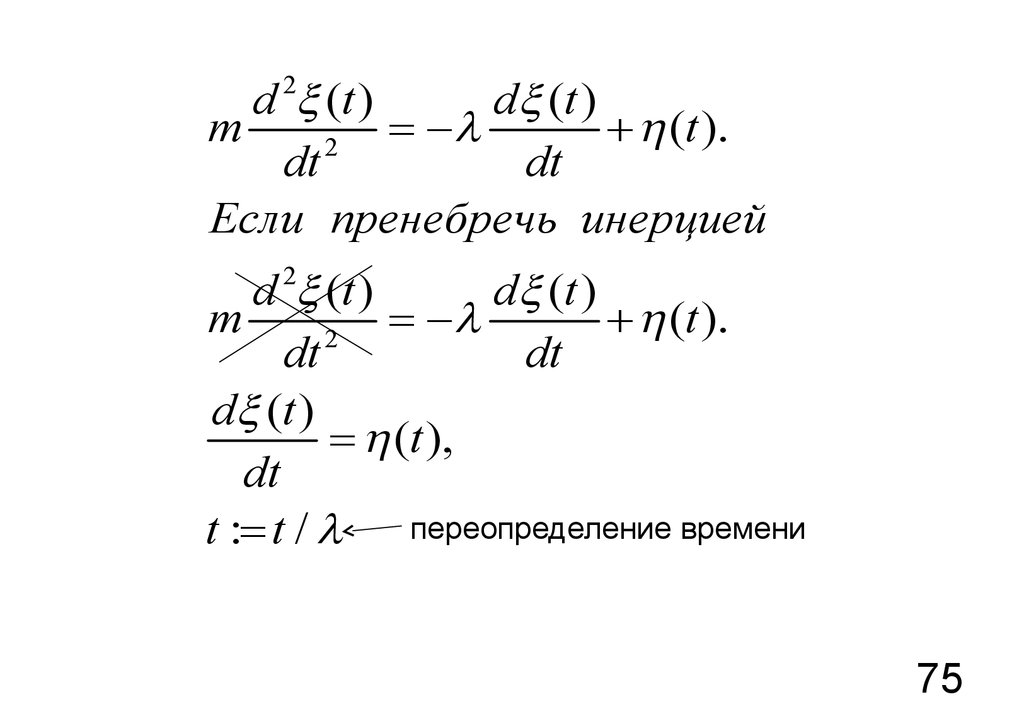

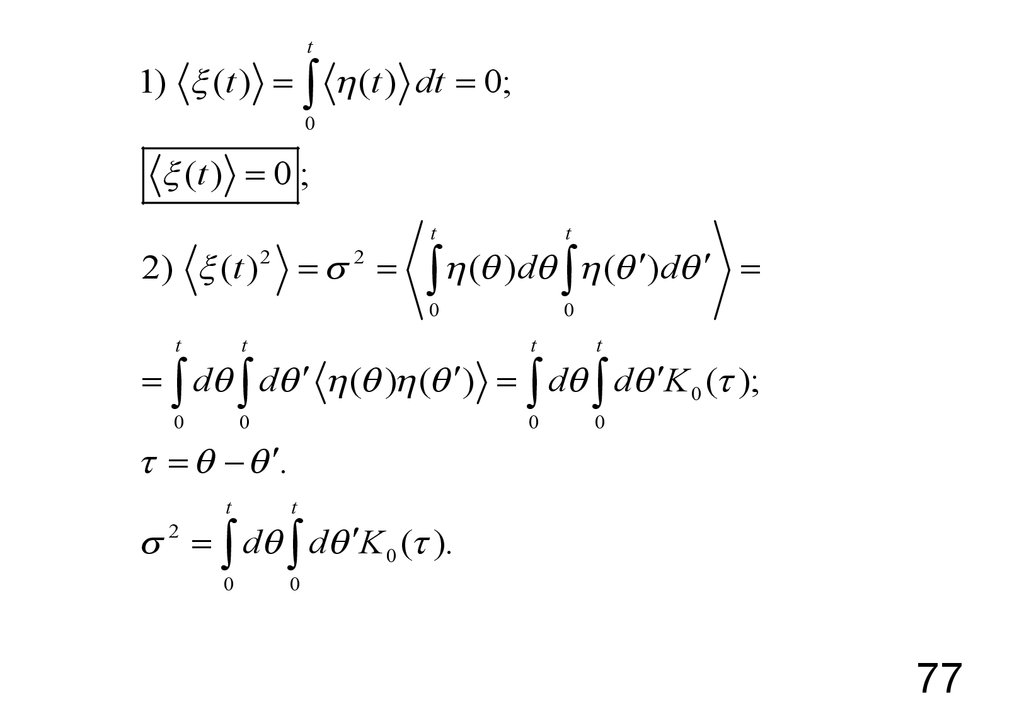
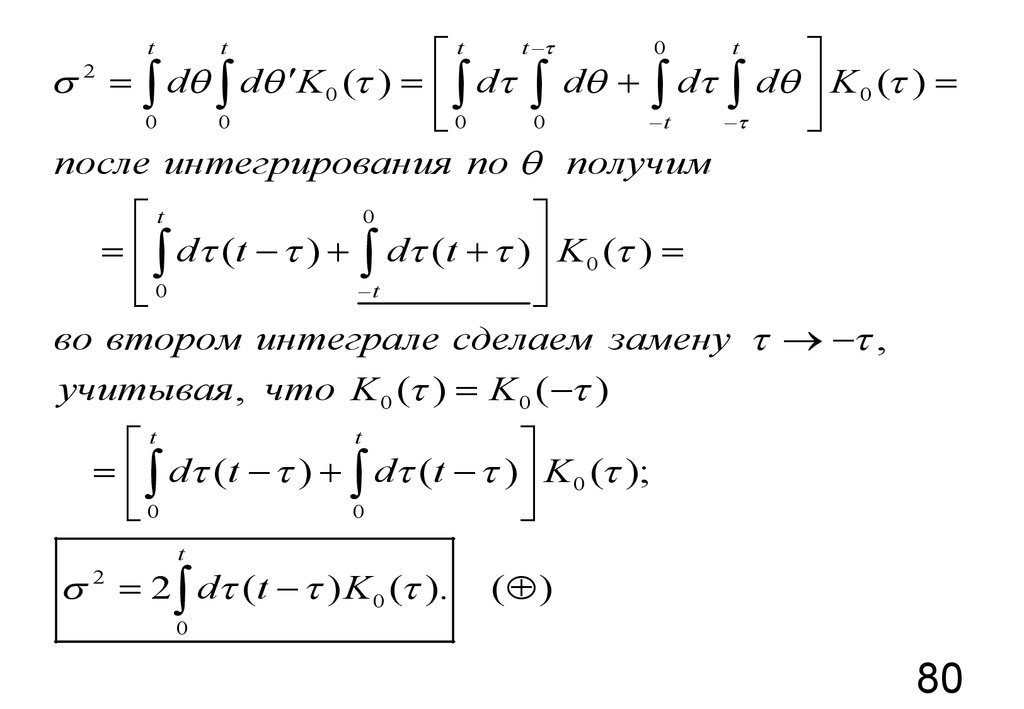
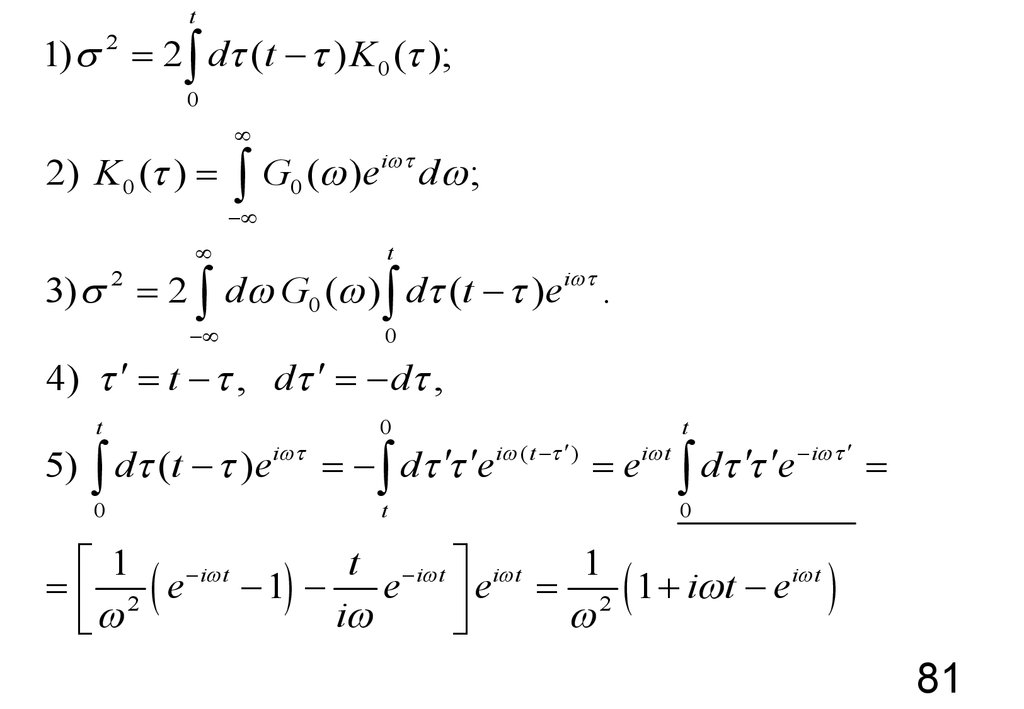





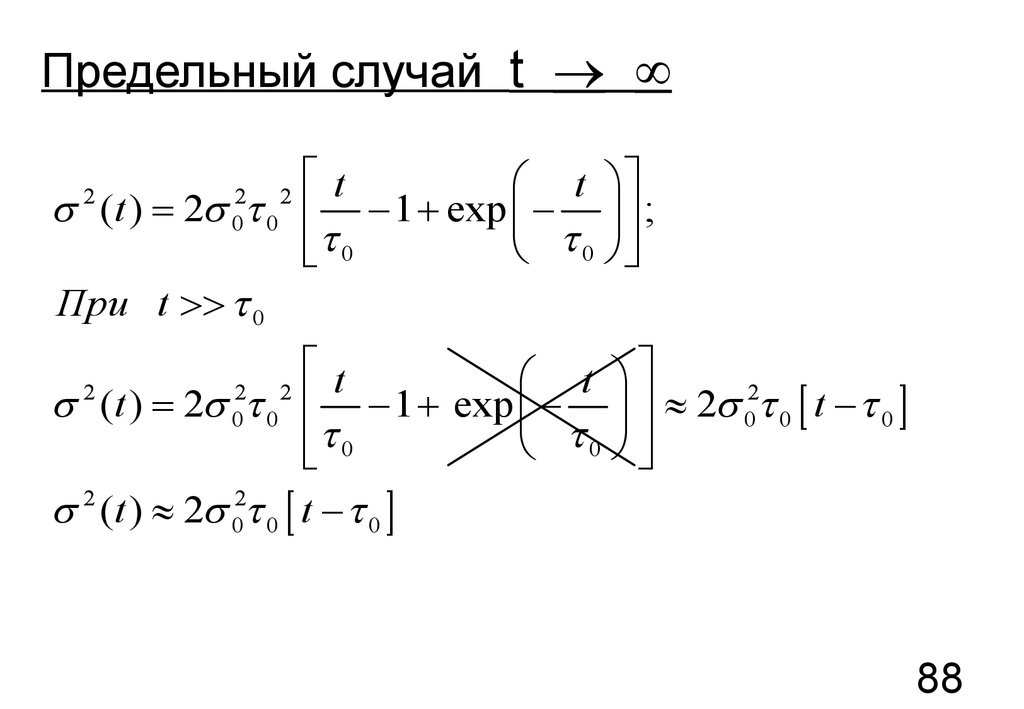




























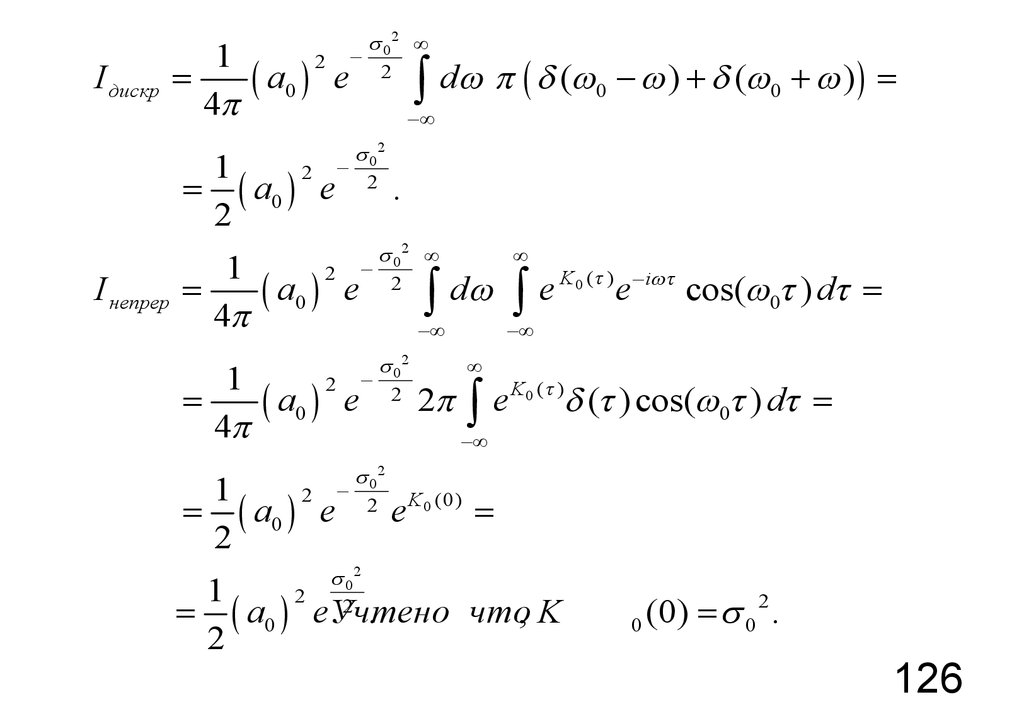








 Математика
Математика Физика
Физика








