Примеры корреляционного и спектрального анализа случайных процессов. Лекція 8

1. Лекція 8 Примеры корреляционного и спектрального анализа случайных процессов

Лекція 8
1
Примеры корреляционного и спектрального анализа
случайных процессов
1. Процесс с экспоненциальной функцией
R A exp
Энергетический спектр этого процесса равен
G
2
R cos d
0
ax
e cos mxdx
0
a
.
a 2 m2
Экспоненциальная АКФ
National Aerospace University
2A
e
d .
0
G
2 A
1
.
2 2
Энергетический спектр

2. Лекція 8 Примеры корреляционного и спектрального анализа случайных процессов

2. Белый шум
Белым шумом называется стационарный -коррелированный случайный
процесс с нулевым средним, спектральная плотность мощности
которого постоянна на всей оси частот, т.е.
R ( )
N0
( );
2
а)
G( f )
N0
, ( f ).
2
б)
Корреляционная функция а) и энергетический спектр б) белого шума
National Aerospace University
2

3. Лекція 8 Примеры корреляционного и спектрального анализа случайных процессов

Термин «белый шум» подчеркивает аналогию с «белым»
(естественным) светом, у которого в пределах видимого диапазона
интенсивность спектральных компонент приблизительно одинакова.
Как видно из выражения для R( ), интервал корреляции белого шума
равен нулю ( 0 = 0). Это означает, что значения белого шума в любые два
сколь угодно близкие моменты времени некоррелированные. Эта модель
шума привлекательна тем, что в большинстве задач возможно
использование фильтрующих свойств -функции.
Найдем среднюю мощность (дисперсию) белого шума
N
Pср G( f )df 0
2
2
df .
Поскольку реальные процессы обладают ограниченной средней
мощностью и конечным временем корреляции ( 0 0), то белый шум
является абстрактной математической моделью и отвечающий ему
физический процесс в природе не существует.
National Aerospace University
3

4. Лекція 8 Примеры корреляционного и спектрального анализа случайных процессов

На практике никогда не требуется рассмотрения всего бесконечного
диапазона частот. Поэтому это полезная математическая идеализация
применяемая в тех случаях, когда в пределах полосы частот
интересующего нас устройства спектральную плотность мощности
внешнего реального шума можно считать постоянной
К определению белого шума в устройствах с ограниченной
полосой пропускания
В частности, этому условию удовлетворяют тепловые шумы
радиотехнических устройств, а также некоторые типы внешних помех
(шумы космоса, активная заградительная шумовая помеха).
National Aerospace University
4

5. Лекція 8 Примеры корреляционного и спектрального анализа случайных процессов

Лекція 8
5
Примеры корреляционного и спектрального анализа
случайных процессов
Шум с постоянной спектральной плотностью мощности на
ограниченном интервале частот называют квазибелым шумом.
Его модель имеет вид
G ( f ) N 0 при 0 f f max
G ( f ) N0
f min f f max .
при
+
+
G (f)
G (f)
0
fmax
f
fmin
Модели квазибелого шума
National Aerospace University
или
fmax
f

6. Лекція 8 Примеры корреляционного и спектрального анализа случайных процессов

Интервал корреляции квазибелого шума отличен от нуля, но
существенно меньше постоянной времени устройства, для синтеза и
анализа которого модель используется. С увеличением fmax или (fmax -
fmіn) обе модели приближаются к модели белого шума.
Если спектральная плотность помехи непостоянна в пределах
интересующего нас частотного диапазона, то шум называют небелым.
Простейшим примером такого шума является пассивная помеха,
созданная отражениями от земной поверхности.
National Aerospace University
6

7. Лекція 8 Примеры корреляционного и спектрального анализа случайных процессов

Лекція 8
7
Примеры корреляционного и спектрального анализа
случайных процессов
3. Процесс со спектром прямоугольной формы с шириной 2 1.
Спектральная плотность процесса постоянна в полосе и равна
2
G0
, где 2 дисперсия (мощность) процесса.
G( )
Среднюю частоту спектра обозначим как
2
0 1
.
2
Будем считать процесс узкополосным, т.е.
G0
0
1
0
2
Спектр
прямоугольной
формы
R G cos d G0 cos
0
National Aerospace University
Тогда
0 .
0
G0
sin
sin
2 cos .
0
1
2
2sin 2
cos 1
2
2
2
2
2
1
2

8. Лекція 8 Примеры корреляционного и спектрального анализа случайных процессов

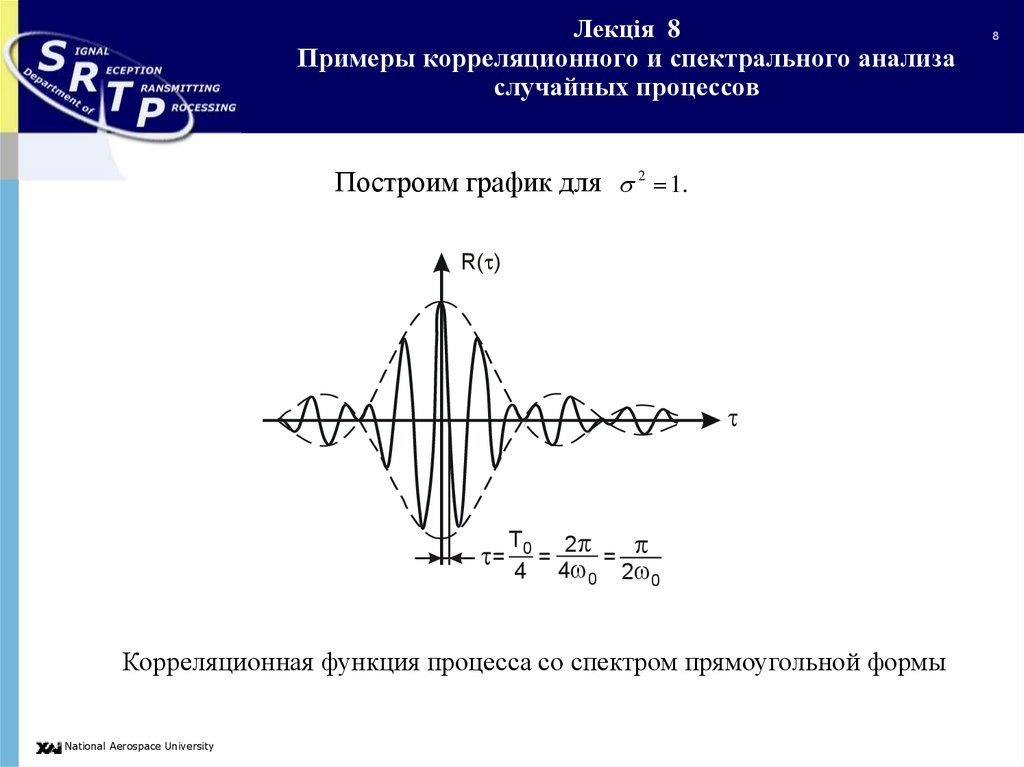
Построим график для 2 1.
R( )
=
T0 2
=
=
4 4 0 2 0
Корреляционная функция процесса со спектром прямоугольной формы
National Aerospace University
8

9. Лекція 8 Примеры корреляционного и спектрального анализа случайных процессов

Лекція 8
9
Примеры корреляционного и спектрального анализа
случайных процессов
Функция носит затухающий характер, причем ее форма определяется
частотами и 0
Выражение для корреляционной функции можно записать в виде
R r cos 0 ,
где r sinc - огибающая корреляционной функции. Такой характер
2
корреляционной функции типичен для узкополосного процесса и имеет
место не только при прямоугольной форме спектра, но и при любой другой
его форме, симметричной относительно средней частоты
заключается только в форме огибающей
National Aerospace University
.
r
. Разница
0

10. Лекція 8 Взаимная спектральная плотность

При рассмотрении двух коррелированных случайных процессов,
например, сигналов на входе и выходе линейной системы, можно
определить пару функций, называемых взаимными спектральными
плотностями.
Пусть мы имеем усеченные реализации случайных процессов x(t ) и y t ,
Фурье преобразования которых равны
T
S x ( ) x(t )e i t dt;
0
T
S y ( ) y t e i t dt.
0
National Aerospace University
10

11. Лекція 8 Взаимная спектральная плотность

Тогда взаимные спектральные плотности мощности этих процессов могут
быть определены как
S x ( ) S y
Gxy lim
;
T
T
S x S y ( )
G yx lim
,
T
T
где - комплексная сопряженность.
National Aerospace University
11

12. Лекція 8 Взаимная спектральная плотность

В отличие от обычных спектральных плотностей, взаимные
спектральные плотности мощности не обязательно должны быть
вещественными, положительными или четными функциями частоты, т.е.
в общем случае функция взаимной спектральной плотности является
комплексной величиной
Gxy Re Gxy i Im Gxy .
Спектры Gxy и Gyx являются комплексно сопряженными, т.е.
Gxy Gyx
.
Взаимные спектры связаны с взаимными корреляционными функциями
преобразованием Фурье (на основе теоремы Винера-Хинчина)
Gxy
Rxy e i d ;
Rxy
National Aerospace University
2
G e d .
i
xy
12

13. Лекція 8 Цифровые методы спектрального анализа

13
Лекція 8
Цифровые методы спектрального анализа
Гармоническая спектральная теория была выдвинута 21 декабря
1807 г. на заседании Французской академии простым инженером Жаном
Батистом Фурье. Суть его доклада заключалась в том, что любая
функция, заданная на конечном участке любой негладкой и даже
разрывной кривой, может быть представлена бесконечной суммой
косинусоидальных и синусоидальных функций.
В начале XX века сэр Артур Шустер предложил численный метод
спектрального анализа временных рядов, заключающийся в вычислении
периодограммы. Для
при
x(n)
n 1,2,...N
National Aerospace University

14. Лекція 8 Цифровые методы спектрального анализа

Лекція 8
14
Цифровые методы спектрального анализа
P
2
1
x (1)e i x (2)e i 2 ... x ( N )e iN .
N
Если временной ряд, например, представляет собой синусоиду с
частотой 0, искаженную некоторой помехой, то периодограмма будет
иметь
максимум
при
= 0. Следовательно, по максимумам
периодограммы можно определить положение частот основных
синусоидальных процессов.
До появления в 1927 г. работы Юла метод периодограмм Шустера был
единственным
анализа.
National Aerospace University
численным
методом
эмпирического
спектрального

15. Лекція 8 Цифровые методы спектрального анализа

Следующий шаг был сделан в классической статье Норберта Винера
по “обобщенному гармоническому анализу” (1930 г.). Ее главный
результат состоял во введении автокорреляционной функции случайного
процесса и получении выражения, связывающего ее преобразование
Фурье со спектральной плотностью мощности (теорема ВинераХинчина).
Шустер рассчитывал периодограмму
P
1
2
x ( ) ,
N
где x ( ) - дискретное преобразование Фурье
National Aerospace University
15

16. Лекція 8 Цифровые методы спектрального анализа

Лекція 8
16
Цифровые методы спектрального анализа
N
x ( ) x ( n )e i n .
n 1
В
том
случае,
когда
синусоидальных
колебаний,
периодограмма
оказывается
стационарный
на
которые
эффективным
процесс
наложен
состоит
белый
средством
из
шум,
выявления
дискретных частот синусоид.
В1949 г. на симпозиуме по применениям корреляционного анализа
Тьюки доложил первую работу по спектральному оцениванию, где
обсуждалось и применение сглаживания дискретного Фурьепреобразования эмпирической корреляционной функции.
National Aerospace University

17. Лекція 8 Цифровые методы спектрального анализа

В результате в практику вошла масса терминов и методов, ставших
классическими в анализе временных рядов: prewhitening –
предотбеливание, aliasing – наложение; smoothing – сглаживание,
tapering – весовая обработка, cepstrum – кепстр и т.д. Редкая работа по
спектральному оцениванию обходиться без упоминания идей и методов
Тьюки.
Согдасно подходу Блэкмана и Тьюки (1958 г.) сначала вычисляются
значения автокорреляционной функции при различных задержках, затем
оценки АКФ взвешиваются (т. е. обрабатывается с помощью функций
окна), после чего вычисляется преобразование Фурье этих взвешенных
оценок АКФ. Вплоть до появления в 1965 году алгоритма БПФ этот метод
был наиболее популярен в спектральном оценивании.
Центральная проблема спектрального оценивания - как получить
спектральную плотность временного ряда на основе ограниченных
данных об автокорреляционной функции.
National Aerospace University
17

18. Лекція 8 Цифровые методы спектрального анализа

Лекція 8
18
Цифровые методы спектрального анализа
Когда
анализируемый
процесс
содержит
детерминированные
составляющие в смеси с шумом, оценка спектра должна делаться очень
внимательно, поскольку возможно получение статистически несостоятельных
результатов.
Необходимость в некоторого рода усреднении по ансамблю, или
сглаживанию выборочного спектра, хорошо видна на примере процессов типа
белого шума, при которых дисперсия спектральной оценки не уменьшалась
даже при использовании все более длинного временного ряда.
Бартлетт предложил разбивать данные на сегменты, вычислять оценки Gˆ ( f )
для каждого сегмента и усреднять периодограммы по всем сегментам.
Аналогичная процедура была предложена Уэлчем для усреднения
периодограмм, полученных с помощью БПФ.
Для аппроксимации усреднения по ансамблю часто используются окна во
временной или частотной областях или же одновременно в обеих. Умножение
реального временного ряда на функцию окна означает, что полное
преобразование является сверткой требуемого
преобразования
с
преобразованием функций окна.
National Aerospace University

19.

Лекція 8
Цифровые методы спектрального анализа
Фрагменты чистого (оранжевый) и зашумлённого (синий) сигналов
National Aerospace University
19

20. Лекція 8 Цифровые методы спектрального анализа

Умножение реального временного ряда на функцию окна означает,
что
полное
преобразование
является
сверткой
требуемого
преобразования с преобразованием функций окна. Если истинный спектр
сигнала сосредоточен в узкой полосе частот, то такая операция свертки
приведет к просачиванию мощности в соседние частотные области.
Помимо искажения спектральной оценки, утечка ухудшает точность
оценивания
мощности
и
обнаруживаемость
синусоидальных
составляющих анализируемого процесса. Боковые лепестки из соседних
частотных ячеек складываются или вычитаются с главным лепестком
отклика в других частотных ячейках спектра, влияя тем самым на оценку
мощности в этой ячейке разрешения.
В предельном случае боковые лепестки сильных частотных
составляющих могут маскировать главные лепестки слабых частотных
составляющих в соседних ячейках.
National Aerospace University
20

21. Лекція 8 Цифровые методы спектрального анализа

Ухудшение наблюдаемости главного лепестка слабого сигнала боковыми
лепестками сильного сигнала
National Aerospace University
21

22. Лекція 8 Цифровые методы спектрального анализа

Широко распространено ошибочное мнение о том, что введение нулей
(zero padding) в последовательность данных перед ее преобразованием
улучшает разрешение периодограммы.
Однако спектр дополненной нулями последовательности служит только
для того, чтобы в интервале частот f 1 t получать дополнительные
2
значения спектральной плотности мощности (СПМ) между значениями
СПМ, полученными по преобразованию исходной последовательности,
не дополненной нулями, т. е. для получения интерполированных
значений СПМ.
National Aerospace University
22

23. Лекція 8 Цифровые методы спектрального анализа

Введение дополнительных нулей полезно для:
сглаживания оценки периодограммы, за счет получения
интерполированных значений;
для уменьшения влияния ошибки “квантования” на точность
оценивания частот спектральных линий.
Основным источником искажений спектра является отсутствие
данных о значениях автокорреляционной функции за пределами
применяемого окна, когда они неявно полагаются равными нулю, что
является, естественно, нереалистическим допущением.
National Aerospace University
23

24. Лекція 8 Цифровые методы спектрального анализа

Современный этап в развитии анализа временных рядов начался с
1965 г. с публикации работы Кули и Тьюки по БПФ. Весь период после
этого идет под знаком существования БПФ для разнообразной
статистической обработки.
С переходом от исходной непрерывной функции x (t ) к
дискретизированной функции f n t , где n - целое число, лежащее в
интервале , , кардинальным образом изменяется ее спектральное
содержание.
Если непрерывная функция будет дискретизирована с интервалом t,
то результат может быть представлен как
x(n t ) x(t ) t , где t
National Aerospace University
t n t .
n

25. Лекція 8 Цифровые методы спектрального анализа

x(t)
0
t
t
x(n t)
а)
а)
t
0
б)
б)
Рис
. 5.1
Графики непрерывной а) и дискретизированной б)
функций
National Aerospace University

26. Лекція 8 Дискретный ряд и дискретное преобразование Фурье (ДПФ)

Рассмотрим две функции, например, детерминированную функцию x (t ) и
ее спектр S ( f ) , удовлетворяющие преобразованию Фурье
1
x (t )
2
S( f )
S (t )ei 2 ft dt;
x (t )e i 2 ft dt.
Пусть спектр сигнала ограничен верхней частотой f в . Тогда по теореме
Котельникова сигнал полностью определяется своими отсчетами,
взятыми через интервал времени t 1/ 2 f в . Но тогда функция x ( n tможет
)
быть представлена как
1
x(n t )
2
где f 0 1/ t.
National Aerospace University
1
i 2 f n t
S
(
f
)
e
df
2
S ( f )e
i 2 n
f
f0
df ,

27. Лекція 8 Дискретный ряд и дискретное преобразование Фурье (ДПФ)

Учитывая, что для временного ряда
1
S t ( f )
S ( f kf 0 ),
t k
можно записать
f0
x(n t ) S t ( f )e
i 2 n
f
f0
df .
0
Функцию S t ( f ), как и любую периодическую функцию, можно разложить
в ряд Фурье, коэффициенты которого определяются выражением
1
f0
f0
S t ( f )e
i 2 n
f
f0
df
0
x(n t )
.
f0
т.е.
National Aerospace University
f
f
i 2 n
x(n t ) i 2 n f0
f0
S t ( f )
e
t x(n t )e
.
f0
n
n

28. Лекція 8 Дискретный ряд и дискретное преобразование Фурье (ДПФ)

Рассмотрим значения функции S t ( f ) N равностоящих точках,
размещенных в интервале от 0 до f 0 , т.е. отсчеты функции, взятые с
интервалом
f
f0
1
в точках f m f , где m 0,1,2,...N 1.
N
N
t
n m
i 2
1
N
S t (m f )
x(n t )e
.
f 0 n
Учитывая, что функция x (t ) реально существует на интервале 0, T ,
т.е. x ( n t ) имеет n 0,1,2,...N 1 отсчетов,
N 1
S m f t x (n t )e
i 2
m n
N
m 0
N 1
x ( n t ) f S m f e
m 0
National Aerospace University
i 2
m n
N
, где f
f0
:
N

29. Лекція 8 Дискретный ряд и дискретное преобразование Фурье (ДПФ)

Эта пара обычно называется парой дискретного преобразования
Фурье (ДПФ). ДПФ является широко применяемым в цифровой технике
методом представления информации.
Прямое ДПФ выполняется над последовательностью дискретных
величин конечной длительности 0 n N 1. В результате получается
также последовательность величин конечной длительности 0 m N 1,
дающая частотно-спектральное представление исходной
последовательности. Каждая из этих последовательностей содержит
одинаковое количество N дискретных величин.
Для сокращения записи можно ввести обозначение
WN e
National Aerospace University
i
2
N
.

30. Лекція 8 Дискретный ряд и дискретное преобразование Фурье (ДПФ)

При этом
N 1
S m t x (n )WNm n
0 m N 1
n 0
N 1
x ( n ) f S m WN mn
0 n N 1
m 0
Приведенные рассуждения справедливы для любой пары функций,
сопряженных по Фурье. В частности, ДПФ может быть использовано для
получения спектральных оценок.
Дискретное представление сигналов по самой своей природе
является приближенным, и основные параметры непрерывного процесса
по его дискретной выборке тоже могут быть определены лишь
приближенно.
National Aerospace University

31. Лекція 8 Дискретный ряд и дискретное преобразование Фурье (ДПФ)

Поэтому необходимо выбрать определенное соотношение между
длительностью T обрабатываемой реализации и полосой частот
исследуемого сигнала, с другой стороны, и основными параметрами
непрерывно-дискретного преобразования t и f , с другой.
Получение периодограммы G(f) предполагает преобразование Фурье
функции времени x(t), заданной на интервале T. Это быстроменяющаяся
функция частоты с интервалом корреляции порядка 1/T.
В соответствии с интервалом не имеет смысла вычислять значения
периодограммы, разделенные меньшим частотным интервалом, чем 1/T,
т.к. также вычисления будут давать коррелированные значения
периодограммы. На основании подобных соображений обычно
утверждают, что удовлетворительно разрешенными можно считать
частотные составляющие, разделенные интервалом f 1/ T .
National Aerospace University

32. Лекція 8 Дискретный ряд и дискретное преобразование Фурье (ДПФ)

Необходимо от вычислений точечной оценки по отдельной
реализации перейти к усреднению по множеству, т.е. иметь k
реализаций длительностью T, для каждой из них вычислить
периодограмму с шагом дискретности 1/T и затем найти для каждой
спектральной составляющей среднее по множеству из k реализаций.
Если процесс стационарный и эргодический, можно выбрать
длительность реализации равной kT, для каждого участка этой
реализации длиной T вычислить значения периодограммы и k
периодограмм усреднить фактически по времени. В этом случае мы
получим
разрешающую
способность
анализа
порядка
1/T
при
статистической точности, определяемой k. Здесь объем обрабатываемой
информации возрастает в k раз.
National Aerospace University

33. Лекція 8 Дискретный ряд и дискретное преобразование Фурье (ДПФ)

Следующая возможность использования периодограммы
заключается в том что, чтобы усреднить значения периодограммы,
вычисленные с шагом f 1/ T , по частотному интервалу. Если в
интервале усреднения f э укладывается k независимых значений
периодограммы, то при условии, что смещение оценки мало, мы
получим статистическую точность примерно такую же, как при
усреднении по множеству, но разрешающая способность анализа будет
определяться величиной f э 1/ m .
National Aerospace University

34. Лекція 2-5 Антенны с ЦОС: основные характеристики и требования к ним, методы обеспечения

Лекція 2-5
34
Антенны с ЦОС: основные характеристики и
требования к ним, методы обеспечения
Если
пространственно-развитая
антенна
представляет
собой
эквидистантную ( x = xn+1 - xn = Const /2) решетку NA однотипных
элементов с всенаправленными излучателями (приемниками), то ДН
определяется в виде
G( )
NA
n 1
2
( x n , ) exp( jk B x n )
A
(2)
где xn [-Lx/2; Lx/2] - координата n-го элемента антенной решетки (АР).
Если А(xn, ) =1, xn [-Lx/2; Lx/2], то
G( )=sin( Lx / )/( Lx / ) = sinc( Lx / )
Положение первого нуля ДН: Lx / = , то есть 0 = /Lx
National Aerospace University

35. Лекція 2-5 Антенны ССС: основные характеристики и требования к ним, методы обеспечения

Рисунок 2 Вид ДН для равноамплитудного распределения
Особенности этой ДН
National Aerospace University
35

36. Лекція 2-5 Антенны ССС: основные характеристики и требования к ним, методы обеспечения

Основные параметры ДН пространственно-развитых антенн:
- ширина главного лепестка (ШГЛ) ДН, которую в большинстве случаев
можно характеризовать для рассматриваемой плоскости либо параметром
0.5, т.е. ШГЛ по уровню -3дБ от максимального значения ГЛ ДН, либо
параметром 0, то есть шириной главного лепестка по нулям ДН;
- уровень максимального бокового лепестка (УМБЛ) ДН, определяемый
амплитудой наибольшего максимума вне области ГЛ [-1; 01[ ] 02; 1] для
нормированных ДН G H (q) = G (q) / Gmax (qГЛ ) ( 01 и 02 определяют
границы ГЛ по нулям, а гл - координату максимума ГЛ);
National Aerospace University
36

37. Лекція 2-5 Антенны ССС: основные характеристики и требования к ним, методы обеспечения

Лекція 2-5
37
Антенны ССС: основные характеристики и
требования к ним, методы обеспечения
соотношение энергии в БЛ ДН к энергии, сосредоточенной в ГЛ ДН
01
02
1
G ( )d G ( )d / G ( )d
02
1
01
Кроме того, важными параметрами антенн и их ДН являются
коэффициент использования поверхности (КИП);
скорость спада боковых лепестков (ССБЛ);
коэффициент направленного действия (КНД)
National Aerospace University
.
(3)

38. Лекція 2-5 Антенны ССС: основные характеристики и требования к ним, методы обеспечения

Лекція 2-5
38
Антенны ССС: основные характеристики и
требования к ним, методы обеспечения
Требования к характеристикам ДН
антенных систем ССС
обеспечение
малой
ширины
главного
лепестка
(ШГЛ)
ДН
(Примечание: параметры 0.5 и 0 обычно достаточно жестко связаны
между собой);
снижение уровня максимального бокового лепестка;
уменьшение соотношения энергии ;
увеличение коэффициента использования поверхности;
обеспечение высокой скорости спада боковых лепестков;
увеличение коэффициента направленного действия;
минимизация размеров и массо-габаритных показателей антенных
систем, обеспечение технологичности их изготовления;
обеспечение простоты аппаратурной или программно-алгоритмической
реализации
амплитудно-фазовых
распредлелений,
обеспечивающих
желаемые характеристики ДН.
National Aerospace University

39. Лекція 2-5 Антенны ССС: основные характеристики и требования к ним, методы обеспечения

Лекція 2-5
39
Антенны ССС: основные характеристики и
требования к ним, методы обеспечения
Метод улучшения характеристик ДН - использование аподизации или
весовых окон. При этом следует учесть, что многие из перечисленных
выше
требований
необходимо
искать
являются
взаимно-противоречивыми,
приемлемый
для
практических
приложений
компромисс.
Аподизация (взвешивание) осуществляются:
путем подстройки коэффициентов усиления в каналах АР;
конструктивно-технологическими методами;
в цифровом виде (в АР с цифровой обработкой сигналов).
National Aerospace University
поэтому

40. Лекція 2-5 Антенны ССС: основные характеристики и требования к ним, методы обеспечения

Оптимизационные задачи:
Обеспечить минимальный УМБЛ ДН при ШГЛ, не хуже заданной (или
обеспечить минимальную ШГЛ при УМБЛ, не выше заданного). Решение
- аподизирующие функции (весовые окна) Дольфа-Чебышева.
АФ Дольфа-Чебышева
National Aerospace University
40

41. Лекція 2-5 Антенны ССС: основные характеристики и требования к ним, методы обеспечения

ДН Дольфа-Чебышева
Основные достоинства и недостатки АФ и ДН Дольфа-Чебышева.
National Aerospace University
41

42. Лекція 2-5 Антенны ССС: основные характеристики и требования к ним, методы обеспечения

Оптимизационные задачи:
Обеспечить минимальное при заданном УМБЛ ДН.
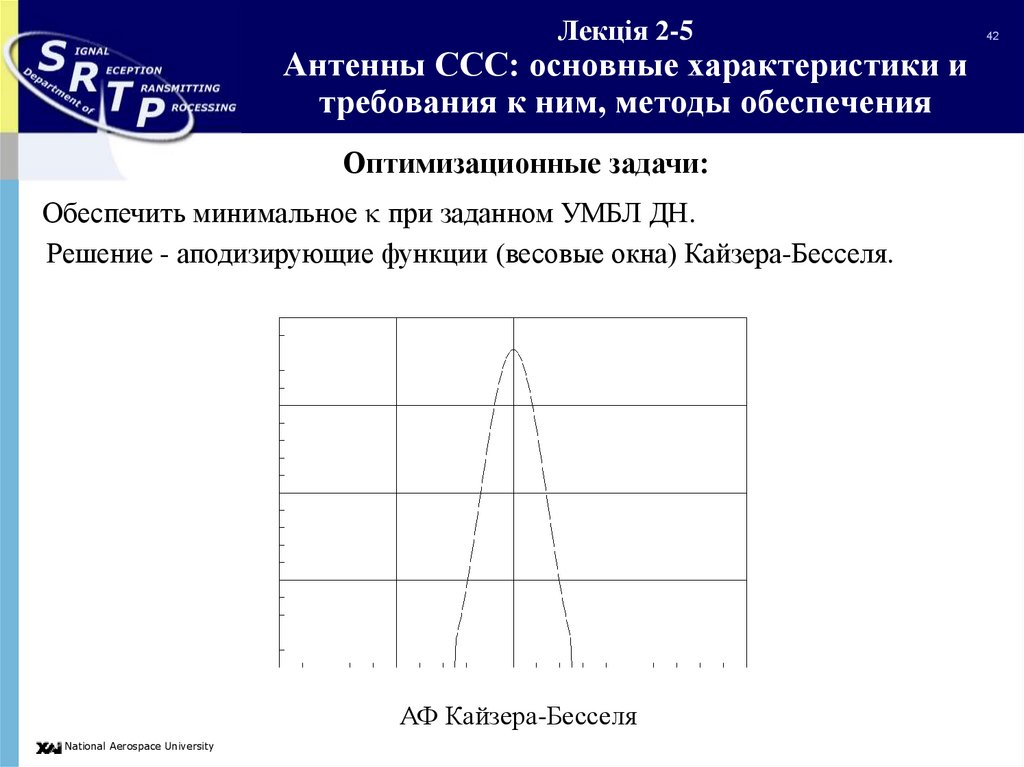
Решение - аподизирующие функции (весовые окна) Кайзера-Бесселя.
АФ Кайзера-Бесселя
National Aerospace University
42

43. Лекція 2-5 Антенны ССС: основные характеристики и требования к ним, методы обеспечения

ДН КайзераБесселя
Основные достоинства и недостатки АФ и ДН Кайзера-Бесселя
National Aerospace University
43

44. Лекція 2-5 Антенны ССС: основные характеристики и требования к ним, методы обеспечения

АФ с быстрым спадом боковых лепестков ДН
Для обеспечения быстрого спада боковых лепестков ДН необходимо
увеличивать номер производной АФ на краях раскрыва (при x = Lx/2),
которая равна 0. Примеры таких АФ - весовые окна семейства
cosa [( p x / Lx )] . С увеличением растет ССБЛ, при этом имеют место
увеличение ШГЛ и уменьшение УМБЛ.
National Aerospace University
44

45. Лекція 2-5 Антенны ССС: основные характеристики и требования к ним, методы обеспечения

АФ cos2 [( p x / Lx )]
ДН для АФ cos2 [( p x / Lx )]
National Aerospace University
45

46. Лекція 2-5 Антенны ССС: основные характеристики и требования к ним, методы обеспечения

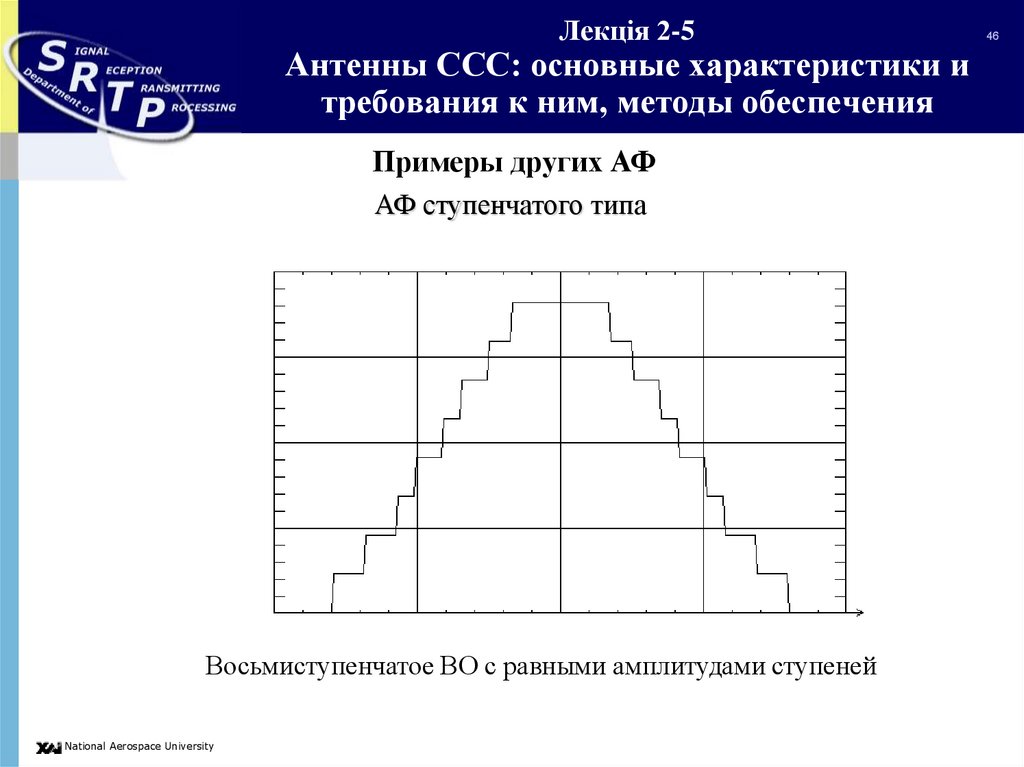
Примеры других АФ
АФ ступенчатого типа
Восьмиступенчатое ВО с равными амплитудами ступеней
National Aerospace University
46

47. Лекція 2-5 Антенны ССС: основные характеристики и требования к ним, методы обеспечения

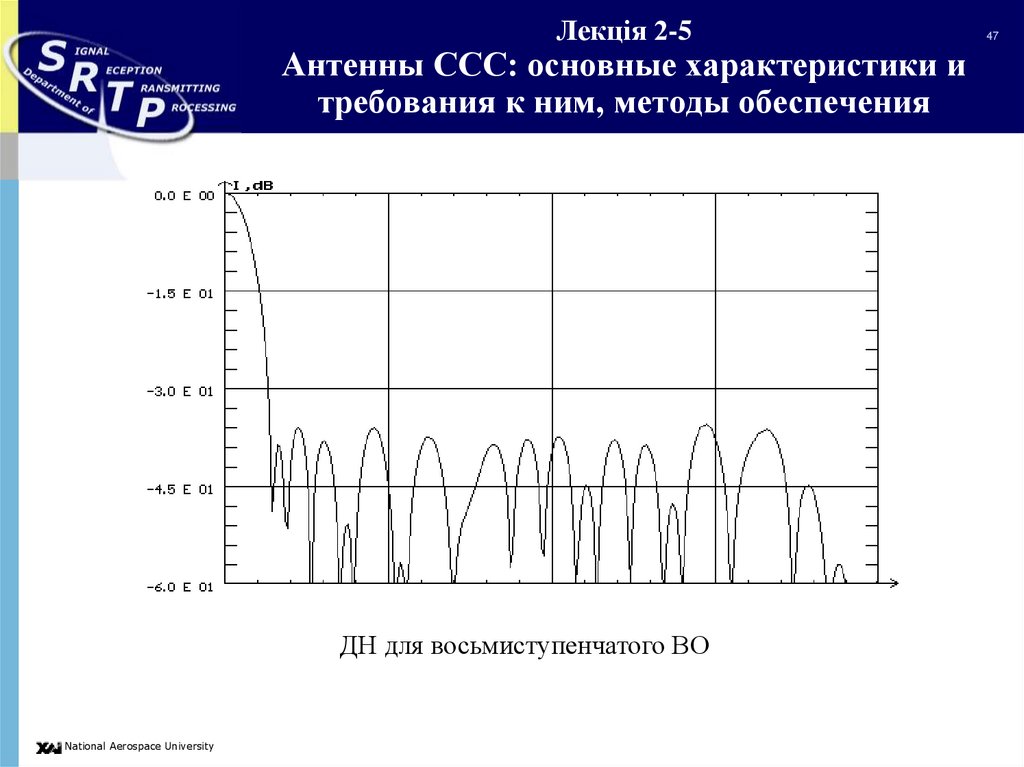
ДН для восьмиступенчатого ВО
National Aerospace University
47

48. Лекція 2-5 Антенны ССС: основные характеристики и требования к ним, методы обеспечения

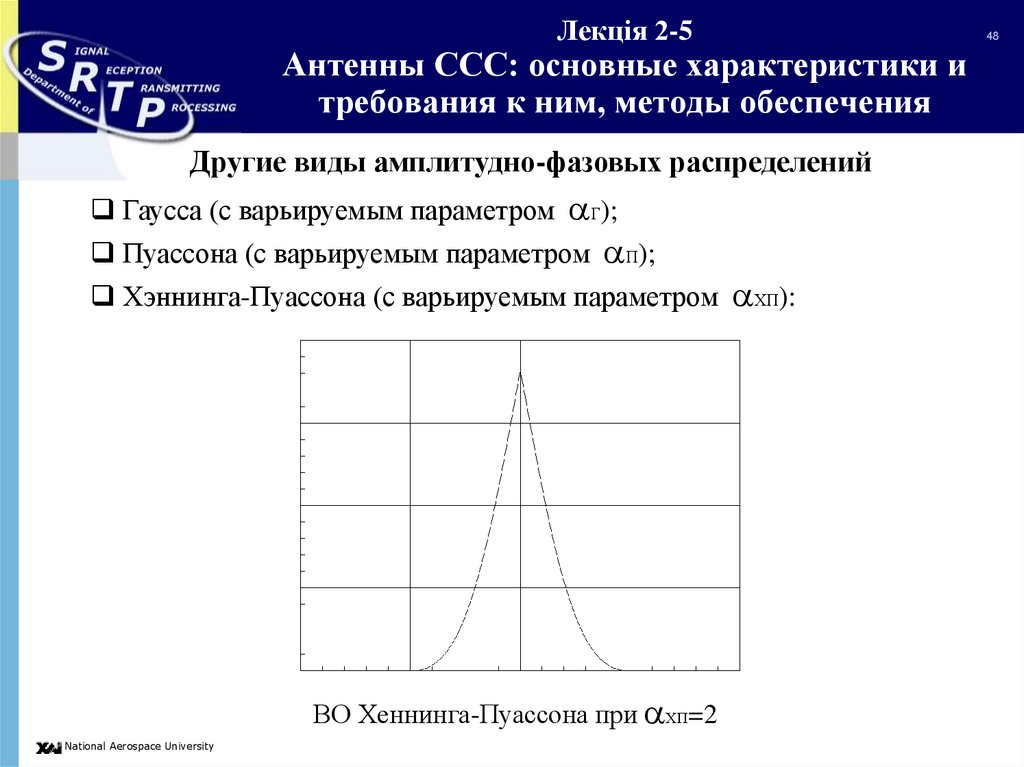
Другие виды амплитудно-фазовых распределений
Гаусса (с варьируемым параметром Г);
Пуассона (с варьируемым параметром П);
Хэннинга-Пуассона (с варьируемым параметром ХП):
ВО Хеннинга-Пуассона при ХП=2
National Aerospace University
48

49. Лекція 2-5 Антенны ССС: основные характеристики и требования к ним, методы обеспечения

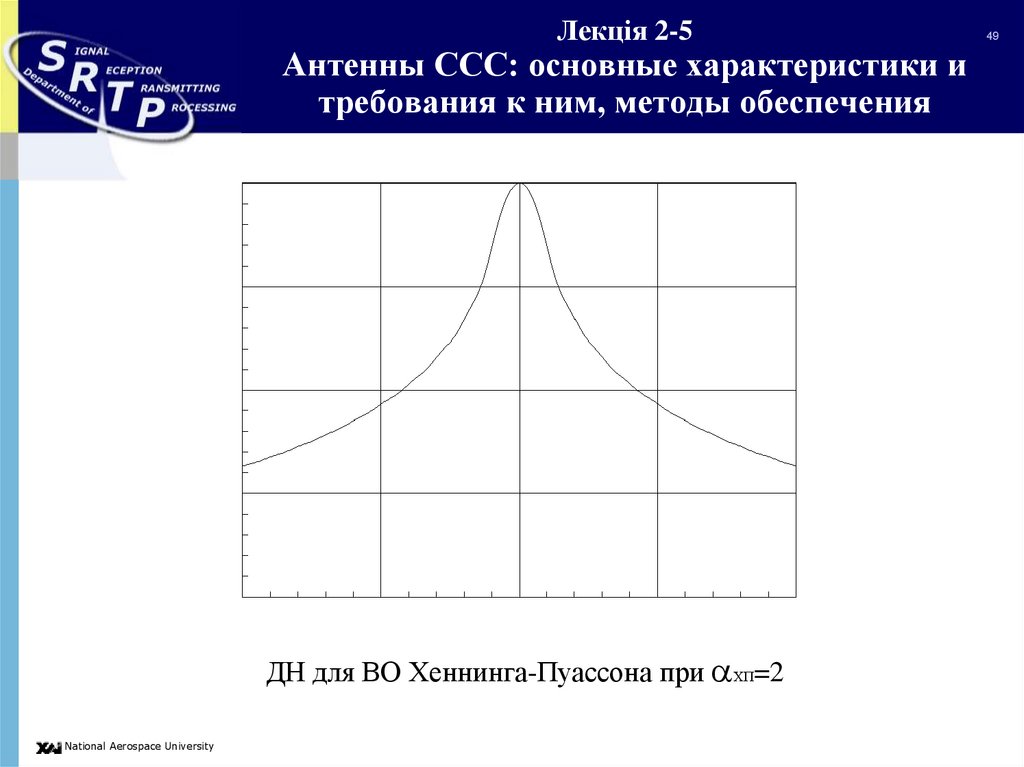
ДН для ВО Хеннинга-Пуассона при ХП=2
National Aerospace University
49

50. Лекція 2-5 Антенны ССС: основные характеристики и требования к ним, методы обеспечения

Лекція 2-5
50
Антенны ССС: основные характеристики и
требования к ним, методы обеспечения
Другие виды амплитудно-фазовых распределений
Абеля-Коши-Пуассона (с варьируемым параметром
Треугольное (Бартлетта):
ВО Бартлетта
National Aerospace University
АКП);

51. Лекція 2-5 Антенны ССС: основные характеристики и требования к ним, методы обеспечения

ДН для ВО Бартлетта
АФ Бомана, АФ Риса, АФ Хэрриса-Блэкмана-Наттола и т.д.
Сканирование ДН осуществляется за счет введения линейного фазового
множителя или использования межэлементных диний задержки.
National Aerospace University
51

52. Лекція 2-5 Антенны ССС: основные характеристики и требования к ним, методы обеспечения

ВО суммарно-разностного типа
К суммарно-разностным ВО принадлежат окна Ханна, Хэмминга и
Блэкмана-Наттола и др.
Полагается, что парциальные ВО wko(x), входящие в сумму
w
a k w k x, Lk
0
0
0
K0
a k0 1
k 0 1
могут быть идентичного типа, например cos [( p x / L )k1, (где k1 - целое
x
число), но при этом wko(x) могут быть определенными (не равными нулю)
на неодинаковых интервалах x [-Lko/2 ;Lko/2], Lko Lx.
National Aerospace University
52

53. Лекція 2-5 Антенны ССС: основные характеристики и требования к ним, методы обеспечения

Таким образом, появляется дополнительная степень свободы для
решения оптимизационных задач, связанная с возможностью
варьировать не только амплитудные коэффициенты ako, число компонент
K и тип парциальных ВО wko(x, Lko), но и параметры {Lko}, вернее,
соотношения {Lko/Lx}.
Это позволяет решать ряд важных задач. Например, используя в
качестве одного из компонент ВО Дирихле с L1=Lx при ako>0, k0 = 2, K 0
можно удовлетворить конструктивно-технологическое требование
w min amin за счет выбора a1.
Таким путем были синтезированы и ВО ступенчатого вида,
показанные ранее.
National Aerospace University
53

54. Лекція 2-5 Антенны ССС: основные характеристики и требования к ним, методы обеспечения

Лекція 2-5
54
Антенны ССС: основные характеристики и
требования к ним, методы обеспечения
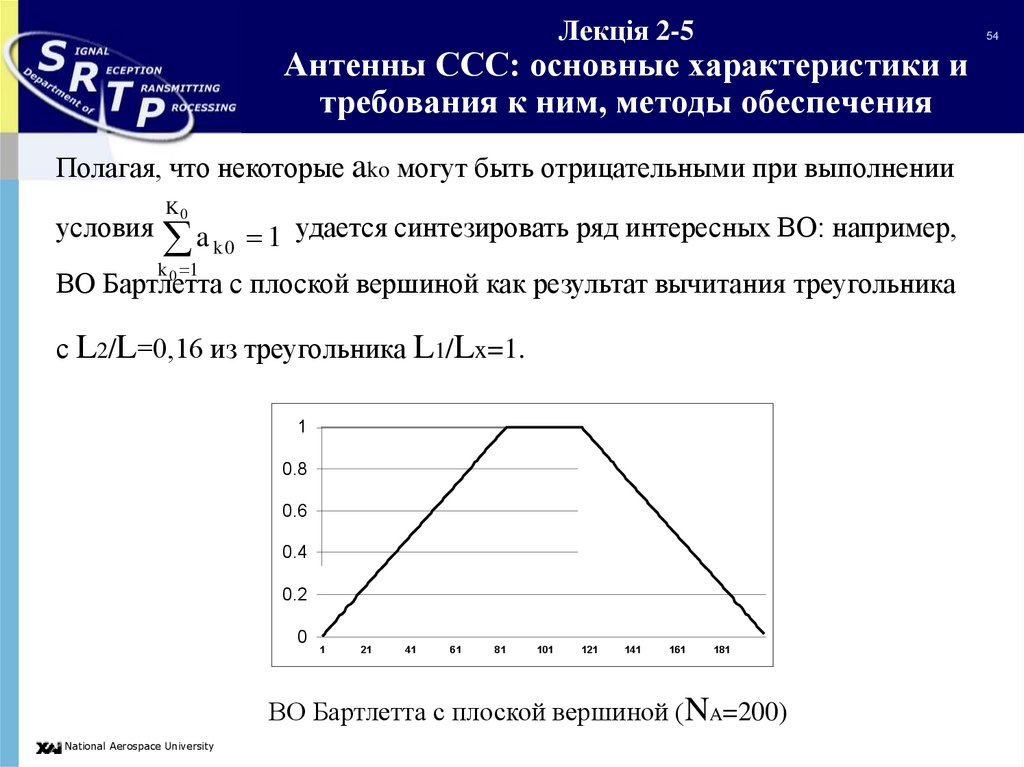
Полагая, что некоторые ako могут быть отрицательными при выполнении
условия
K0
a k0 1
удается синтезировать ряд интересных ВО: например,
k 1
0
ВО Бартлетта
с плоской вершиной как результат вычитания треугольника
с L2/L=0,16 из треугольника L1/Lx=1.
1
0.8
0.6
0.4
0.2
0
1
21
41
61
81
101
121
141
161
181
ВО Бартлетта с плоской вершиной (NA=200)
National Aerospace University

55. Лекція 2-5 Антенны ССС: основные характеристики и требования к ним, методы обеспечения

0
-10
-20
-30
-40
-50
-60
-70
-80
-90
-100
ДН G( ), дБ, для ВО Бартлетта с плоской вершиной
Для такого ВО по сравнению с оригиналом УМБЛ ДН снижается на 5 дБ
и при этом на 3% сужается ГЛ.
National Aerospace University
55