Неопределенный интеграл и методы его решения

1.

Неопределенный интеграл и
методы его решения

2.

Понятие неопределенного интеграла
В дифференциальном исчислении решается задача:
по данной функции f(x) найти ее производную.
Интегральное исчисление решает обратную задачу:
найти функцию F(x) , зная ее производную F’(x) = f(x).
Функция F(x) называется первообразной функции
f(x) на интервале (a; b), если x a, b :
F ( x ) f ( x )
Например :
1. f ( x) 3 x 2 , тогда F ( x) x 3 , т.к. ( х 3 ) 3 х 2
2. f ( x) sin x, тогда F ( x) cos x, т.к. ( cos x) sin x

3.

Понятие неопределенного интеграла
Теорема
Если функция F(x) является первообразной функции f(x) на (a; b),
то множество всех первообразных для f(x) задается формулой:
F(x) + С, где С – постоянное число.
Доказательство:
F ( x ) C f ( x )
F(x) + С – первообразная функции f(x) .
Например :
f ( x) 2 x, тогда F ( x) x 2 , т.к. ( х 2 ) 2 х
F ( x) x 2 5, f ( x) x 2 4 и т.д. F ( x) x 2 C , C R

4.

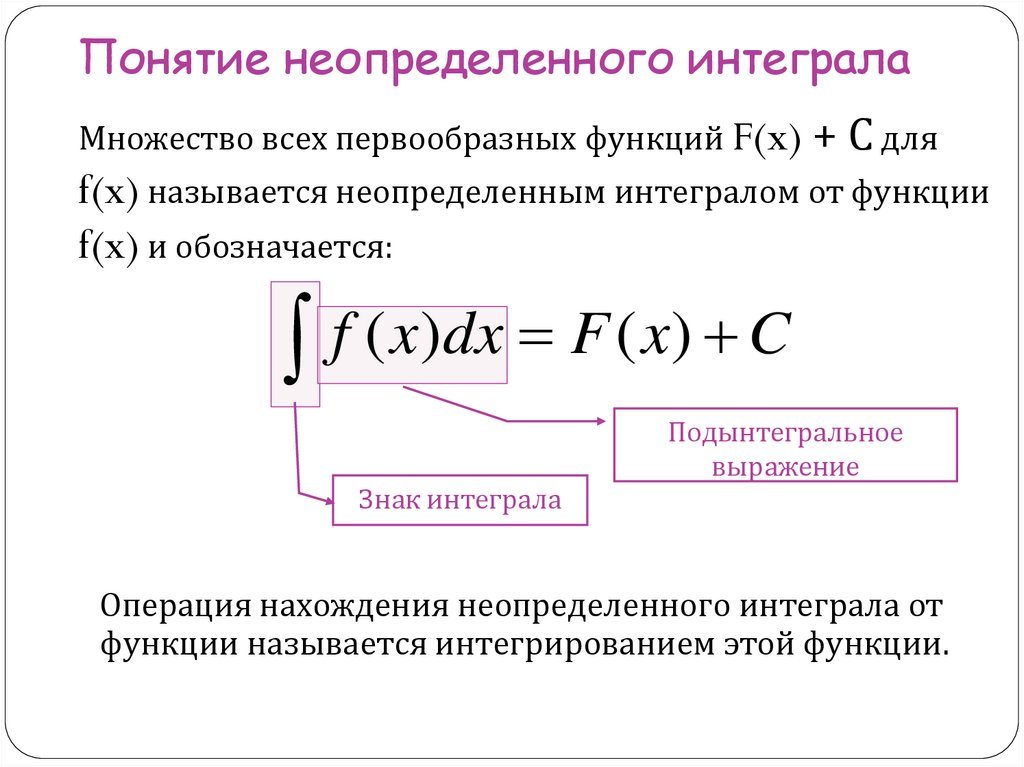
Понятие неопределенного интеграла
Множество всех первообразных функций F(x) + С для
f(x) называется неопределенным интегралом от функции
f(x) и обозначается:
f
(
x
)
dx
F
(
x
)
C
Знак интеграла
Подынтегральное
выражение
Операция нахождения неопределенного интеграла от
функции называется интегрированием этой функции.

5.

Свойства неопределенного интеграла
Неопределенный интеграл от суммы (разности) конечного числа
непрерывных функций равен сумме (разности) интегралов:
f ( x ) f ( x ) dx f ( x )dx f ( x )dx
1
2
1
2
Инвариантность формулы интегрирования: Если
то:
f
(
x
)
dx
F
(
x
)
C
f (u ) du F (u ) C
где u = φ(x) – произвольная функция, имеющая непрерывную
производную.
1
f (ax b) dx a F (ax b) C
1
f (ax ) dx a F (ax ) C
f ( x b) dx F ( x b) C

6.

Таблица неопределенных интегралов
1. dx x C .
a 1
x
2. x a dx
C, (a 1) .
a 1
dx
3. ln x C .
x
x
a
4. a x dx
C .
ln a
5. e x dx e x C .
6. sin xdx cos x C .
7. cos xdx sin x C .
dx
8. 2 ctgx C .
sin x
dx
9. 2 tgx C .
cos x

7.

Непосредственное интегрирование
Метод интегрирования, при котором данный интеграл путем
тождественных преобразований подынтегральной функции и
применения свойств неопределенного интеграла приводится к
табличным
интегралам,
называется
непосредственным
интегрированием.
e 2x 6 dx e dx 2x dx 6 dx
x
x
e x dx 2 x dx 6 dx e x x 2 6 x C
2
2
1
sin
x
cos
x
2
ctg x dx sin2 x dx sin2 x dx
1
1
1 dx
dx dx ctg x x C
2
2
sin x
sin x

8.

n 1
x
x dx n 1 C , n 1
1
1
dx
x
x
dx ln x C , n 1
n
Примеры
Пример 1.
Вычислить x 2 3x 3 x 1 dx .
Решение.
2
3
2
3
x
3
x
x
1
dx
x
dx
3
x
dx xdx dx .
x3
x4 x2
3
x C
3
4
2

9.

Примеры
Пример 2.
Вычислить
Решение.
n 1
x
n
x
dx n 1 C , n 1
1
1
dx
x
x
dx ln x C , n 1
5
x 3 dx
3 1
x
5
3
x 3 dx 5 x dx 5 3 1 C
x 2
5
5
C 2 C
2
2x

10.

Примеры
n 1
x
n
x
dx n 1 C , n 1
1
1
dx
x
x
dx ln x C , n 1
Пример 3.
Вычислить
2
x
6 x 2 dx
Решение.
2
3
2
3
2
x
6
x
2
dx
6
x
2
x
dx
6
x
dx
2
x
dx
4
x
x3
3x 4 2 x 3
6 2 C
C
4
3
2
3

11.

Примеры
Пример 4.
n 1
x
n
x
dx n 1 C , n 1
1
1
dx
x
x
dx ln x C , n 1
x 10 x 2
dx
x
2
Вычислить
Решение.
2
x 10 x 2
x
10 x 2
dx
dx
x
x
x
x
1
x2
x dx 10 dx 2 dx
10 x 2 ln x С
x
2
2

12.

x
a
x
x
x
a
dx
C
,
е
dx
е
C
ln a
sin xdx cos x C , cos xdx sin x C
1
1
cos 2 x dx tgx C , sin 2 x dx ctgx C
Примеры
Пример 5.
Вычислить
Решение.
6
x
5 3 cos x cos 2 x dx
6
x
x
5
3
cos
x
dx
5
dx 3 cos x dx
2
cos x
x
1
5
6
dx
3 sin x 6 tgx C
2
cos x
ln 5

13.

Метод интегрирования подстановкой
(заменой переменной)
Метод интегрирования подстановкой заключается во введении
новой переменной интегрирования.
Пусть требуется вычислить интеграл
f ( x )dx.
Сделаем подстановку: x= (t) , где φ – функция, имеющая
непрерывную производную. Тогда:
dx (t )dt
Получим формулу интегрирования подстановкой:
f
(
x
)
dx
f
(
(
t
))
(t ) dx
Иногда целесообразно подбирать подстановку в виде t= (x)
Тогда подынтегральную функцию нужно представить в виде:
f ( ( x )) ( x ) dx f (t )dt.
t
dt

14.

Метод интегрирования подстановкой
(заменой переменной)
x 3 t;
1. x x 3 dx x t 2 3;
dx (t 3) dt 2tdt
2
t 2 3 t 2t dt 2t 4 6t 2 dt
5
3
t
t
2 t dt 6 t dt 2 6 C
5
3
2
5
3
x 3 2 x 3 C
5
4
2

15.

Метод интегрирования подстановкой
(заменой переменной)
2.
ex
e 2
x
dx
e x 2 t;
dt e x 2 dx e x dx
1
2
1
dt
t
x
2
t
dt
C
2
e
2 C
t
1
2

16.

Метод интегрирования подстановкой
(заменой переменной)
F (kx b)
f (kx b) dx k C
sin 6 x
3. cos 6 x dx
C
6
9
9
(
3
x
2
)
(
3
x
2
)
4. (3 x 2)8 dx
C
C
9 3
27
ln 1 2 x
ln 1 2 x
1
5.
dx
C
C
1 2x
2
2
1
ctg 3 x 2
2ctg 3 x 2
6.
dx
C
C
2
sin 3 x 2
32
3

17.

Метод интегрирования по частям
Пусть u = u(x) и v = v(x) - функции, имеющие непрерывную
производную. Тогда:
d (u v ) u dv v du
Интегрируя это равенство, получим:
d (uv ) udv vdu uv udv vdu
udv uv vdu
Формула интегрирования по
частям
Интегрирование по частям состоит в том, что подынтегральное
выражение представляется в виде произведения двух
сомножителей: u и dv , затем, после нахождения du и v
используется формула.
Иногда эта формула применяется несколько раз.

18.

Метод интегрирования по частям
Типы интегралов, которые удобно вычислять по частям:
Интегралы вида:
kx
P ( x ) sin kx dx;
P
(
x
)
e
dx
;
P ( x ) cos kx dx
где: P(x) – многочлен. Удобно положить u = P(x), dv – остальные
сомножители.
P ( x ) arcsin kx dx;
P
(
x
)
ln
x
dx
;
P
(
x
)
arctg
kx
dx
;
Интегралы вида:
Удобно положить dv = P(x)dx, u – остальные сомножители.
Интегралы вида:
ax
ax
e
sin
bx
dx
;
e
cos bx dx
интегралы приводятся к исходному, за u можно принимать любой
сомножитель.

19.

Метод интегрирования по частям
u 2x 1;
dv e 2 x dx;
2x
2x 1 e dx du (2x 1) dx 2dx
dv
u
1 2x
2x
v dv e dx e
2
2 x 1 0.5e
u
v
2x
0.5e
v
2x
2dx
du
x 0.5 e 2 x e 2 x dx
x 0.5 e
2x
0.5e
2x
C x e
2x
C

20.

Метод интегрирования по частям
e x sin 4 x dx
u
dv
u ex;
dv sin 4 xdx;
du (e x ) dx e x dx
1
v dv sin 4 xdx cos 4 x
4
e ( 0.25 cos 4 x ) ( 0.25 cos 4 x e )dx
x
x
0.25e x cos 4 x 0.25 cos 4 x e x dx
0.25e x cos 4 x 0.25 1
I1

21.

Метод интегрирования по частям
u e ;
dv cos 4 xdx;
x
1 e x cos 4 x dx
u
dv
du (e x ) dx e x dx
1
v dv cos 4 xdx sin 4 x
4
e x 0.25 sin 4 x 0.25 sin 4 x e x dx
e x 0.25 sin 4 x 0.25
0.25e x cos 4 x 0.25(0.25e x sin 4 x 0.25 )
1 x
e (sin 4 x 4 cos 4 x) С
17

22.

Домашнее задание
1. Вычислить интегралы:
3 2
x x 10 dx
‫׬‬
5 4 х 3 cos x dx
‫