Похожие презентации:
Неопределенный интеграл
1.
НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ2.
§1. Первообразная функции. Неопределенныйинтеграл и его свойства. Таблица основных
неопределенных интегралов.
В дифференциальном исчислении решается задача:
по данной функции
F ( x)
найти ее производную
F ( x) f ( x).
Интегральное исчисление решает обратную задачу:
найти функцию
производная
F ( x), если известна ее
f ( x) F ( x).
3.
Определение 1. ФункцияF (x)
первообразной функции
f ( x),
некотором множестве
X,
называется
заданной на
если для
выполняется равенство
F ( x) f ( x).
x X
4.
Пример. Пустьf ( x) x .
3
Тогда первообразной для данной функции является функция
4
x
F ( x) ,
4
так как
4
x 1
3
3
F ( x) 4 x x f ( x).
4 4
5.
Очевидно, что первообразными будут также любые функции4
x
F ( x)
C,
4
где
C const ,
поскольку
4
x
x
F ( x) C C
4
4
1
3
3
4 x 0 x f ( x).
4
4
6.
F (x) и (x) − двепервообразные одной и той же функции f ( x ), то
Таким образом, если
( x ) F ( x ) C.
7.
Определение 2. Множествовсех первообразных функции
X
F ( x) C
f (x) на множестве
называется неопределенным интегралом
и обозначается
f ( x)dx F ( x) C.
8.
Здесь− знак интеграла,
f (x)
− подынтегральная функция,
f ( x)dx
x
− подынтегральное выражение,
− переменная интегрирования.
9.
Нахождение первообразной для данной функцииназывается интегрированием функции
Теорема. Для всякой непрерывной на
функции
f (x)
f (x)
f ( x ).
(a; b)
существует на этом промежутке
первообразная, а, значит, и неопределенный интеграл.
10.
Геометрически неопределенный интеграл представляетсобой семейство кривых, зависящих от одного параметра
C,
которые получаются одна из другой путем
параллельного сдвига вдоль оси
Oy.
11.
Перечислим основные свойства неопределенногоинтеграла:
f ( x)dx f ( x);
1)
2)
3)
Cf
(
x
)
dx
C
f
(
x
)
dx
,
f ( x)dx f ( x) C ;
C const ;
12.
4)(
f
(
x
)
g
(
x
))
dx
f
(
x
)
dx
g
(
x
)
dx
,
5) Если
то
где
f ( x)dx F ( x) C ,
f (u )dx F (u ) C ,
u (x ) − произвольная функция, имеющая
непрерывную производную.
13.
6) Еслиf ( x)dx F ( x) C ,
то
1
f (kx b)dx F (kx b) C
k
для
k , b R, k 0
14.
Приведем таблицу основных неопределенныхинтегралов:
1)
dx
x
C
;
n 1
2)
3)
x
x
dx
C
,
(
n
1);
n 1
n
dx
x
C
;
2 x
15.
4)dx
;
C
x
ln
x
5)
e
dx
e
C
;
x
x
x
6)
a
a
dx
C
;
ln a
7)
cos
xdx
sin
x
C
;
x
16.
8)sin
xdx
cos
x
C
;
9)
1
dx
tgx
C
;
cos2 x
1
dx
ctgx
C
;
10)
sin 2 x
1
11)
dx
arctgx
C
;
1 x2
17.
12)13)
14)
15)
1
1 x
2
dx arcsin x C ;
1
1
x
a 2 x 2 dx a arctg a C;
1
x
dx arcsin C ;
2
2
a
a x
1
x a
2
dx ln x x a C.
2
18.
Приведенные в данной таблице интегралыназывают табличными.
19.
§2. ОСНОВНЫЕ МЕТОДЫ ИНТЕГРИРОВАНИЯ.2.1. Метод непосредственного интегрирования.
Непосредственным интегрированием называют
интегрирование с помощью свойств 3, 4 и 6,
тождественных преобразований
подынтегральной функции и таблицы основных
интегралов.
20.
Примеры.1)
dx
1
5
dx
x
dx
5
5
x x
5 1
4
x
x
1
C
C 4 C;
5 1
4
4x
21.
2)1
2
x
xdx
x
x
dx
x
3
1
3
2
3
7
2
7
1
2
9
2
x
x
dx x dx
C C
7
9
1
2
2
2 9
2 8
2 4
x C
x x C x x C;
9
9
9
22.
3)dx
3 x
2
dx
3
2
x
2
x
arcsin
C;
3
23.
4)7
x
5sin x 4 x dx
1
5 sin xdx 4 dx 7 dx
x
x
x
4
5cos x
7 ln x C;
ln 4
24.
x 2x xdx
5
x
1
3
5
4
x
2x
x
5 5 5 dx
x
x
x
5
3
5)
x
1
5
3
4
1
2 dx
x
25.
143
1
x dx 2 dx dx
x
14
1
3
x
2 x ln x C
14
1
3
3
x
11
11
3
2 x ln x C;
26.
65
3
7
6
5
3
7
6)
dx
dx
5x
5x 5x
x
x
7
6 3
5
x
x
7
dx 6 dx 3 dx
5
x
6x 3
x
7
5
ln
x
7
5
C;
27.
7)cos(5x 1)dx
f ( x)dx F ( x) C
1
f (kx b)dx F (kx b) C ;
k
cos
x
dx
sin
x
C
,
k
5,
b
1
F ( x)
f ( x)
1
sin(5 x 1) C;
5
28.
8)1
2
2 9 xdx 2 9 x dx
f ( x)dx F ( x) C
1
f (kx b)dx F (kx b) C ;
k
1
3
2 2
2
x
dx
x
C
,
k
9,
b
2
3
f ( x)
F ( x)
29.
32
1 2
2 9x C
9 3
2
3
2 9 x C.
27
30.
2.2. Метод поднесения под знакдифференциала и замены переменной.
На практике часто встречаются интегралы вида
f ( x) ( x)dx
или интегралы, которые сводятся к такому виду
31.
Подведем в этом интеграле множитель( x)
под знак дифференциала:
( x)dx d ( x) ,
а затем произведем подстановку
( x ) t.
В результате получим формулу подстановки в
неопределенном интеграле:
32.
f ( x) ( x)dx ( x)dx d ( x)f ( x) d ( x) t ( x) f (t )dt
33.
Следовательно, задача свелась к нахождению интегралаf (t )dt ,
который либо уже табличный, либо легко сводится к
табличному, и обратной подстановке
t ( x ).
34.
Примеры поднесения под знак дифференциала:a, b const, a 0
dx d ( x b);
1
dx d (ax);
a
1
dx d (ax b);
a
35.
12
xdx d ( x ),
2
1
2
xdx
d (ax b);
2a
1
n 1
x dx
d (ax b), n 1;
2a (n 1)
n
36.
1dx d ln x ;
x
1
1
dx d a ln x b ;
x
a
1
cos(ax b)dx d sin(ax b) ;
a
37.
1sin(ax b)dx d cos(ax b) ;
a
e dx d (e b);
x
x
1
x
a dx
d (a b);
ln a
x
38.
11
dx
d
tg
(
ax
b
)
;
2
cos (ax b)
a
1
1
dx d ctg (ax b) ;
2
sin (ax b)
a
39.
11 x
2
1
1 x
2
dx d arcsin x ;
dx d arccos x ;
40.
1dx
d
arctgx
;
2
1 x
1
dx
d
arcctgx
.
2
1 x
41.
Примеры.1)
1
1
sin 4 xdx dx 4 d (4 x) sin 4 x 4 d (4 x)
1
sin 4 xd (4 x) t 4 x
4
1
1
1
sin tdt cos t C cos 4 x C;
4
4
4
42.
2)dx
1
dx
d
(6
x
5)
6 x 5 6
1 d (6 x 5)
t 6 x 5
6
6x 5
1 dt 1
1
ln t C ln 6 x 5 C;
6 t 6
6
43.
13) cos 2 x sin 2 xdx sin 2 xdx d cos 2 x
2
4
1
4
cos 2 x d cos 2 x t cos 2 x
2
5
1 4
1 t
1
5
t dt C cos 2 x C;
2
2 5
10
44.
4)4
1
ln x
1
1
4
dx ln x dx dx d ln x
x
x
x
ln x d ln x t ln x
1
4
5
4 54
4
t dt 1 C t C ln x 4 C;
5
5
4 1
1
4
t
1 1
4
45.
5)dx
1
1
dx
tg 4 x cos2 4 x tg 4 x cos2 4 x
1
1
2 dx d tg 4 x
4
cos 4 x
1
1
d tg 4 x t tg 4 x
4 tg 4 x
1 1
1
1
dt ln t C ln tg 4 x C ;
4 t
4
4
46.
6)3
arcsin 6 x
1 36 x
2
dx arcsin 6 x
3
1
1 (6 x)
2
dx
1
d arcsin 6 x
6
1
3
arcsin 6 x d arcsin 6 x t arcsin 6 x
6
4
1 3
1 t
1
4
t dt C arcsin 6 x C;
6
6 4
24
47.
arctg 3 x7)
2
1
arctg 3 x
dx
2
dx
2
1 9 x2
1 (3x)
1
d arctg 3 x
3
1
arctg 3 x
2
d arctg 3x t arctg 3x
3
t
arctg 3 x
1
1 2
2
t
2 dt
C
C;
3
3 ln 2
3ln 2
48.
12
8) x 2 x 1 dx xdx
d
2
x
1
4
2
4
4
1
2
2
2
2 x 1 d 2 x 1 t 2 x 1
4
2 x 1
1 4
1 t
t
t dt C
C
C;
4
4 5
20
20
5
5
2
5
49.
9)x
3
2
7x 4
3
7 x 4
3
13
dx
1
3
7x 4
3
x dx
2
1
2
3
x dx x dx d 7 x 4
21
2
13
1
3
3
3
7 x 4 d 7 x 4 t 7 x 4
21
50.
13 12
3
1
1 t
1 t
13
t dt 1 C 2 C
21
9 3 1
9 3
2
1 3 23
1
3
3
t C 3 x 4 C.
21 2
14
51.
2.3. Метод интегрирования по частям.Пусть
u u ( x)
и
v v( x)
дифференцируемые функции. Тогда справедлива
следующая формула интегрирования по частям:
udv
uv
vdu
(2.1)
52.
С помощью этой формулы вычисление интегралаudv
сводится к отысканию другого интеграла
vdu
Применение формулы целесообразно в тех случаях, когда
интеграл
vdu
более прост для нахождения, чем
исходный, либо подобен ему.
53.
При этом в качествеu
следует брать такую функцию,
которая при дифференцировании упрощается, а в качестве
dv
ту часть подынтегрального выражения, интеграл
от которого известен или может быть найден. Иногда
формулу (2.1) приходится применяться несколько раз.
Укажем некоторые типы интегралов, которые удобно
вычислять методом интегрирования по частям.
54.
1. Интегралы видаP
(
x
)
sin
kxdx
,
n
P
(
x
)
cos
kxdx
,
n
P
(
x
)
e
dx
,
n
kx
P
(
x
)
a
dx
,
n
kx
55.
Pn ( x)где
многочлен,
k
число.
Удобно положить
u Pn ( x),
а
dv sin kxdx,
cos kxdx,
kx
e dx,
kx
a dx
соответственно.
56.
Тогда формулу (2.1) надо применять столько раз, каковастепень многочлена
Pn ( x), т.е. n
раз.
57.
2. Интегралы видаP
(
x
)
ln
kxdx
,
n
P
(
x
)
arcsin
kxdx
,
n
P
(
x
)
arccos
kxdx
,
n
58.
P(
x
)
arctgkxdx
,
n
P
(
x
)
arcctgkxdx
n
59.
В этом случаеu ln kx,
arcsin kx,
arccos kx,
arctgkx,
arcctgkx
а
соответственно,
dv Pn ( x)dx.
60.
3. Интегралы видаe
sin
bxdx
,
ax
e
cos
bxdx
ax
Можно положить
u e
ax
или
u sin bx (u cos bx)
61.
Примеры.1)
x
4 cos 2 xdx
2
dv
u
u x 4 du d ( x 4) ( x 4) dx 2 xdx
dv cos 2 xdx v cos 2 xdx 1 sin 2 x(C 0)
2
2
2
2
1
1
( x 4) sin 2 x sin 2 x 2 xdx
2
2
du
u
2
v
v
62.
2x
( 2) sin 2 x x sin 2 xdx
2
u
dv
u x du dx
1
dv sin 2 xdx v sin 2 xdx cos 2 x
2
2
x
( 2) sin 2 x
2
1
1
x cos 2 x cos 2 x dx
2
du
u 2
v
v
63.
2x
x
1
( 2)sin 2 x cos 2 x cos 2 xdx
2
2
2
2
x
x
1
( 2)sin 2 x cos 2 x sin 2 x C
2
2
4
x
1
x
2 sin 2 x cos 2 x C
4
2
2
2
x 7
x
sin 2 x cos 2 x C;
2
2 4
2
64.
2)ln 5x (4 x
u
3
6 x 3)dx
dv
1
1
u ln 5 x du d (ln 5 x) (ln 5 x) dx 5 x 5dx x dx
dv (4 x3 6 x 3)dx v (4 x3 6 x 3)dx
4
2
x
x
4
2
4 6 3x x 3x 3x
4
2
65.
1ln 5 x ( x 3x 3x) ( x 3x 3x) dx
x
u
v
v
4
2
4
2
du
ln 5 x ( x 3 x 3 x) ( x 3 x 3)dx
4
2
3
4
x 3 2
ln 5 x ( x 3x 3x) x 3x C
4 2
4
2
66.
2.4. Интегрирование рациональных дробей.Определение. Рациональной дробью называется
функция, заданная в виде отношения двух многочленов:
n 1
Pn ( x) an x an 1 x ... a1 x a0
m
m 1
Qm ( x) bm x bm 1 x ... b1 x b0
n
67.
Если степень многочлена числителя меньше степенимногочлена знаменателя, т.е.
n m,
то рациональная дробь называется правильной;
в противном случае, т.е. если
n m,
дробь называется неправильной.
68.
Простейшей дробью называется правильная дробьодного из следующих типов:
1.
A
;
x a
2.
A
(k 2, k );
k
( x a)
3.
A
2
( D p 4q 0);
2
x px q
69.
4.5.
где
Ax B
2
(
D
p
4
q
0);
2
x px q
x
Ax B
2
px q
(k 2, k ,
k
A, a, B, p, q
D p 4q 0),
2
70.
2.4.1. Интегрирование простейшихрациональных дробей.
Интегрирование простейших рациональных дробей
рассмотрим на примерах.
71.
Примеры.1)
t
dx
1 d (2 x 5)
2x 5 2 2x 5
t
1 dt 1
ln t C
2 t 2
1
ln 2 x 5 C ;
2
72.
t2)
dx
1 d (3 7 x)
(3 7 x)4 7 (3 7 x)4
t
3
1 dt
1 4
1 t
4 t dt C
7 t
7
7 3
1
1
C
C;
3
3
21t
21(3 7 x)
73.
3)dx
1
dx
I
2 x 2 2 x 10 2 x 2 x 5
Выделим в знаменателе последнего подынтегрального
выражения полный квадрат.
74.
Тогда1















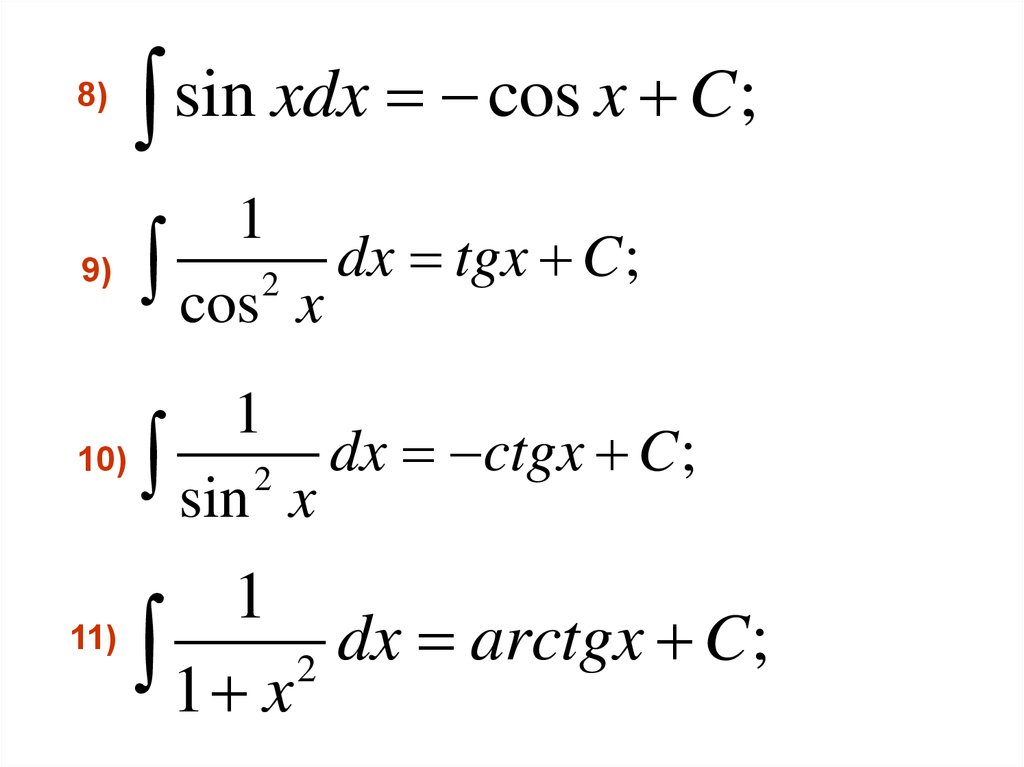
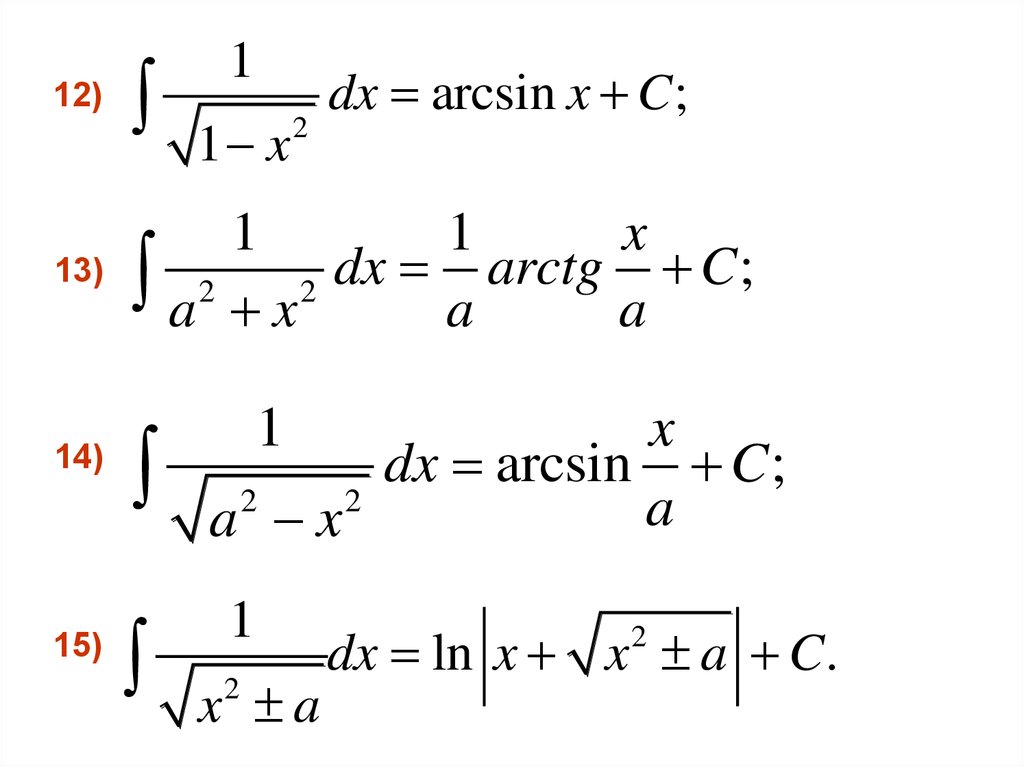



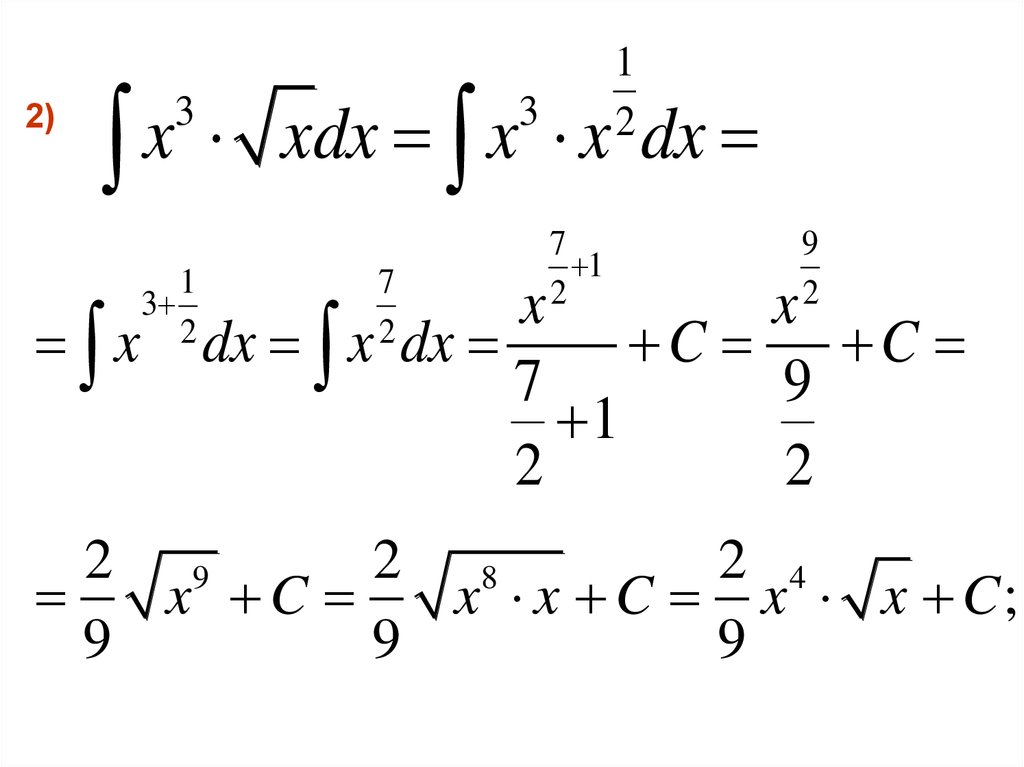
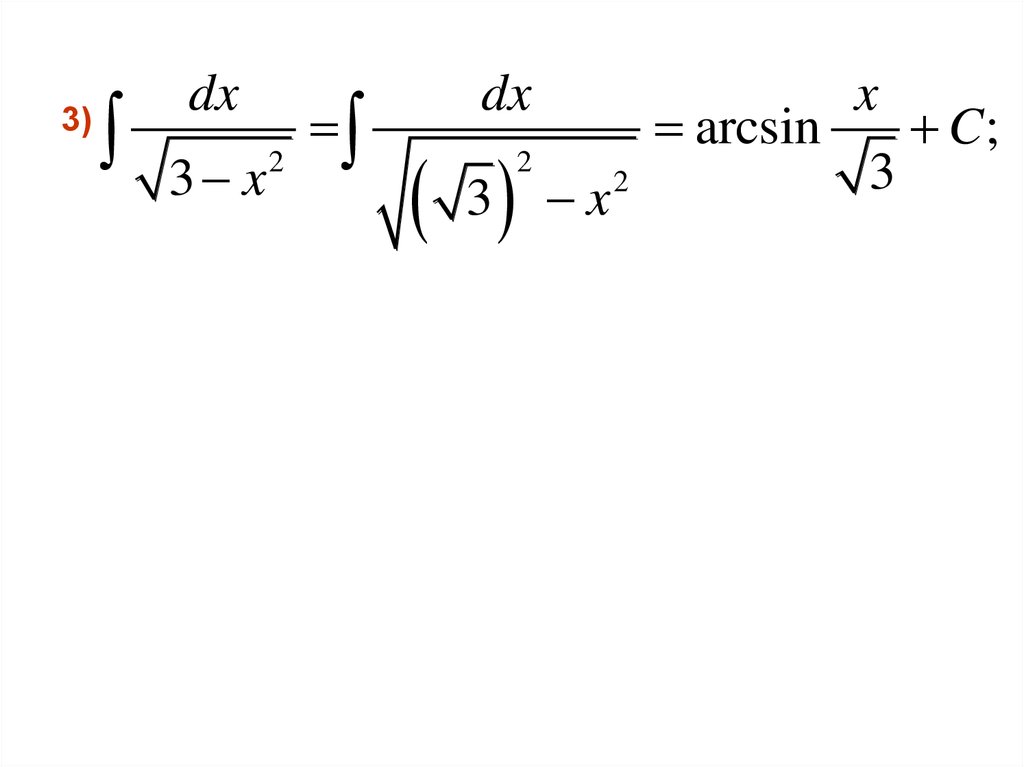


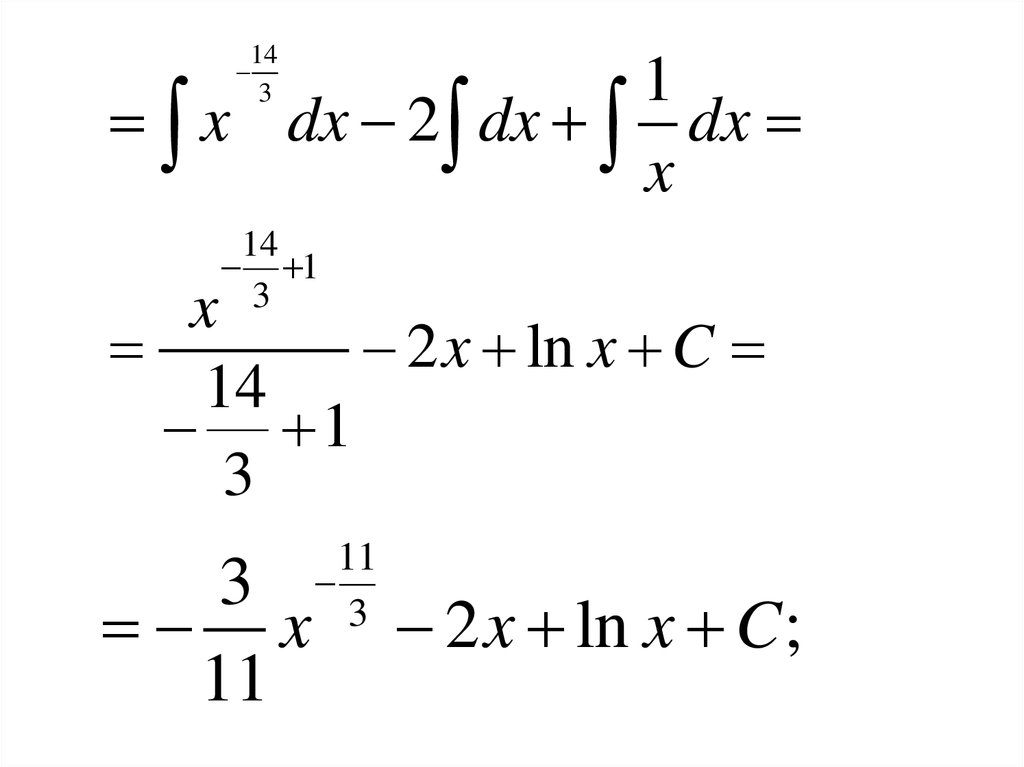

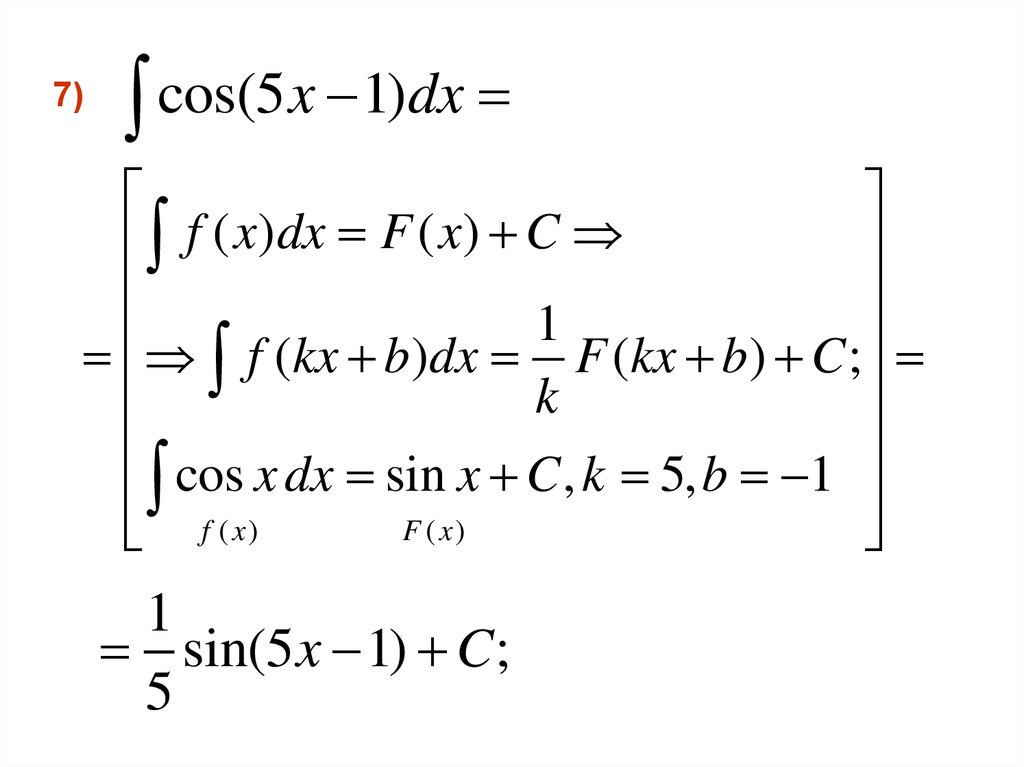
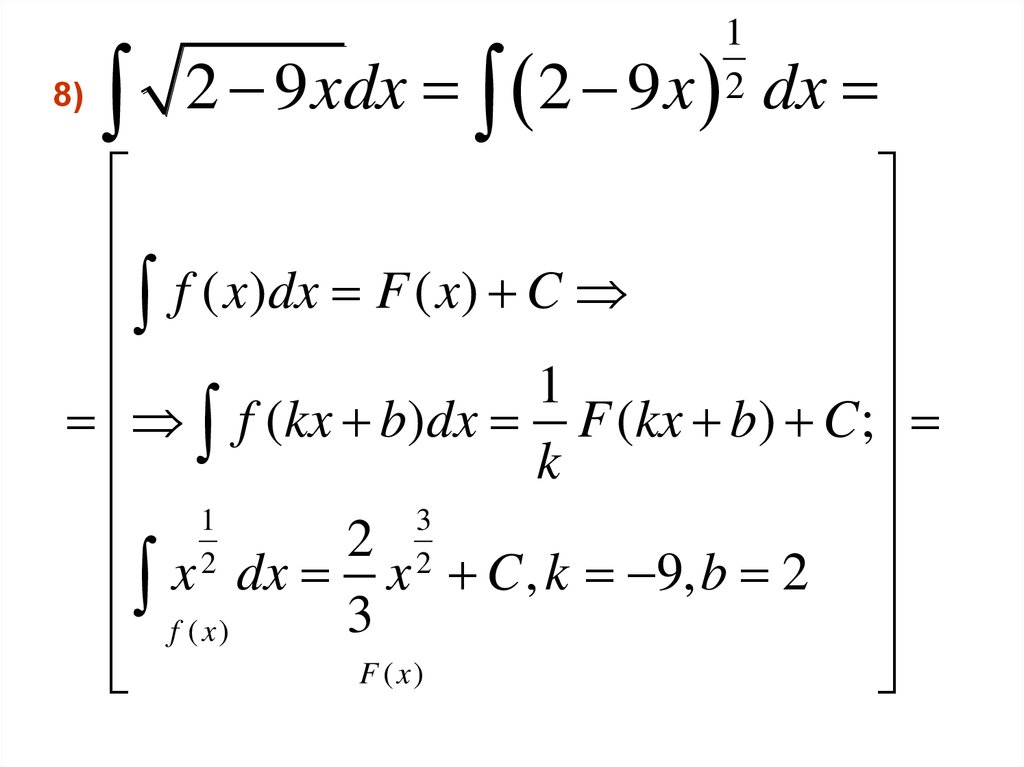
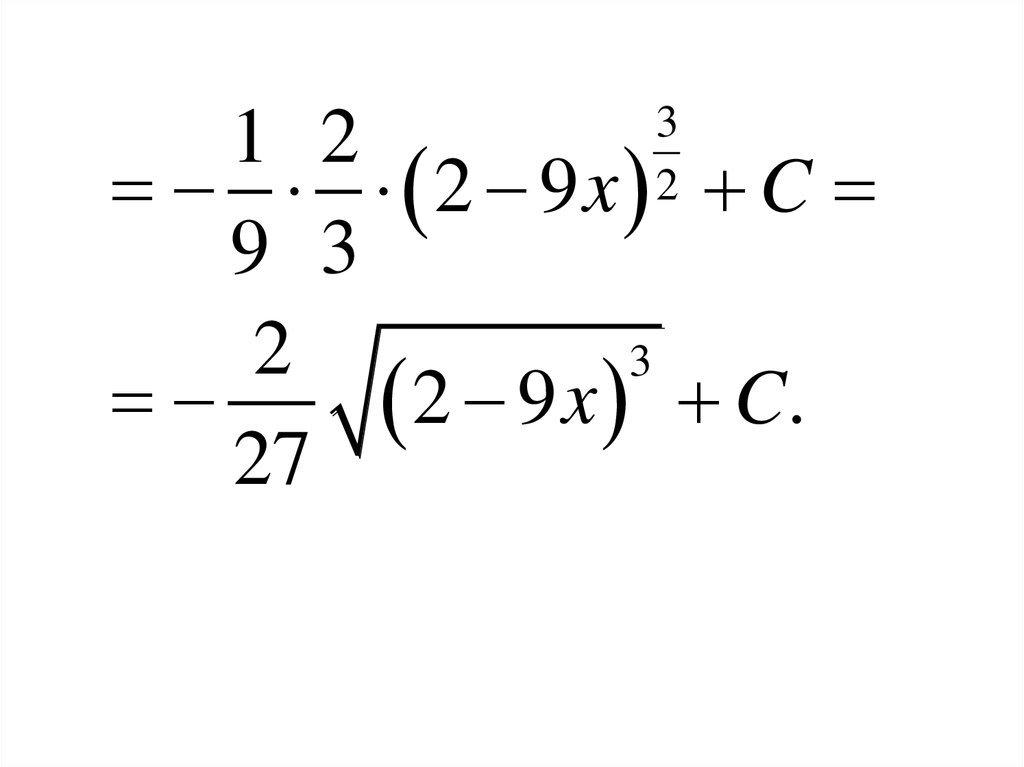


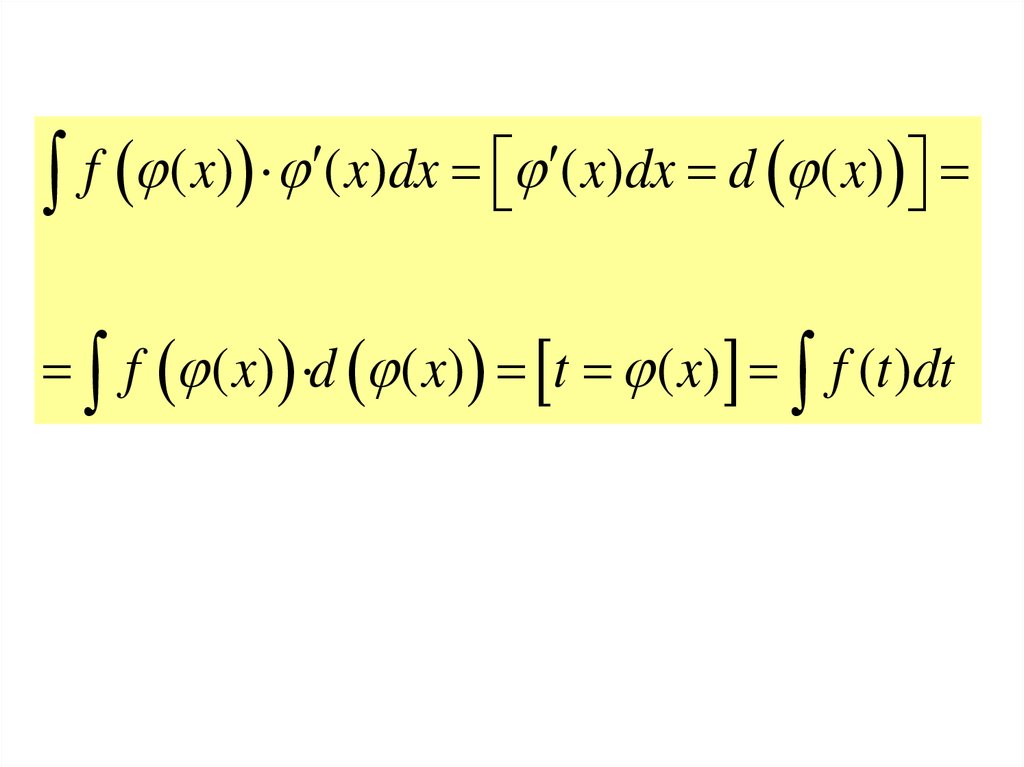



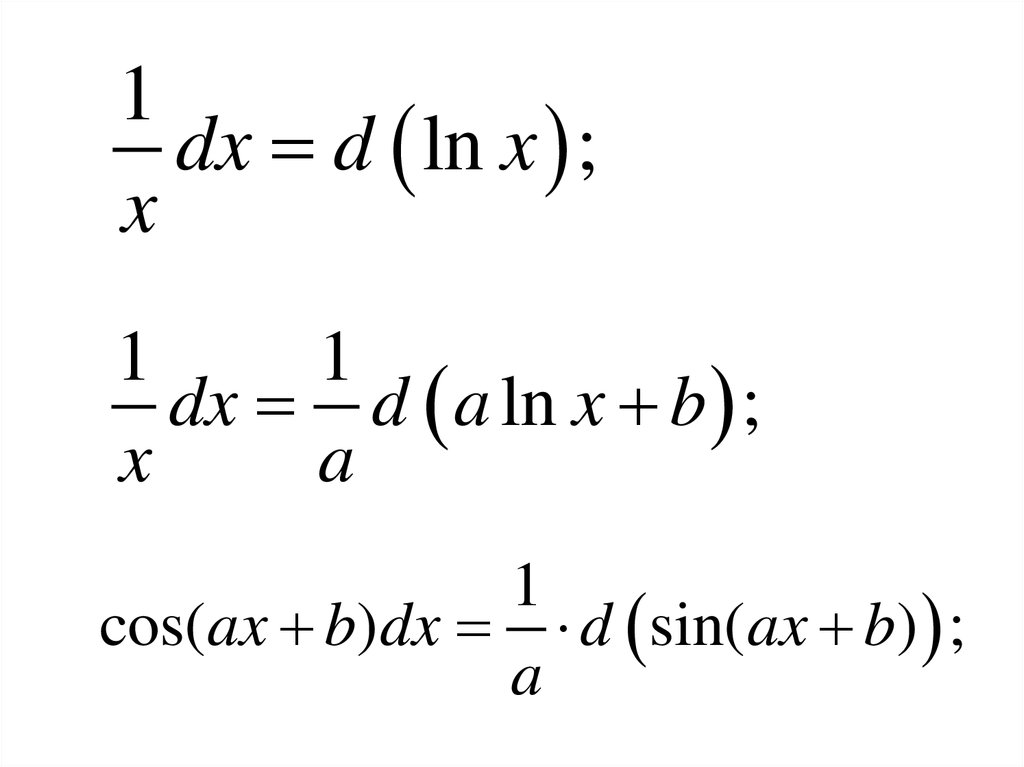


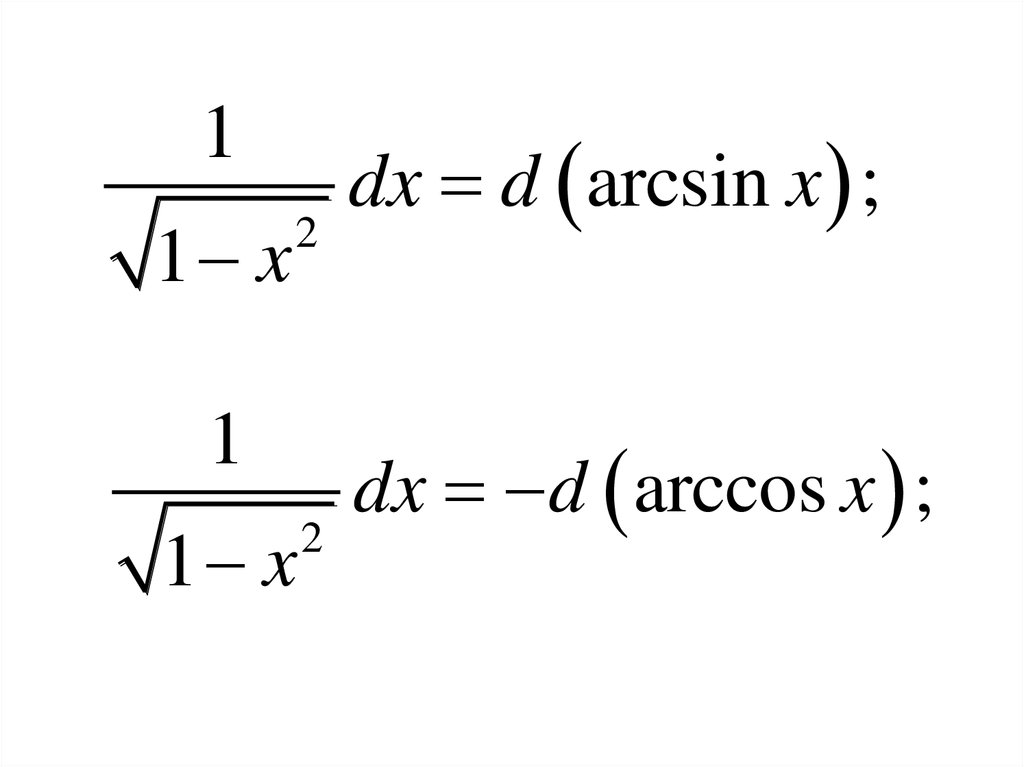

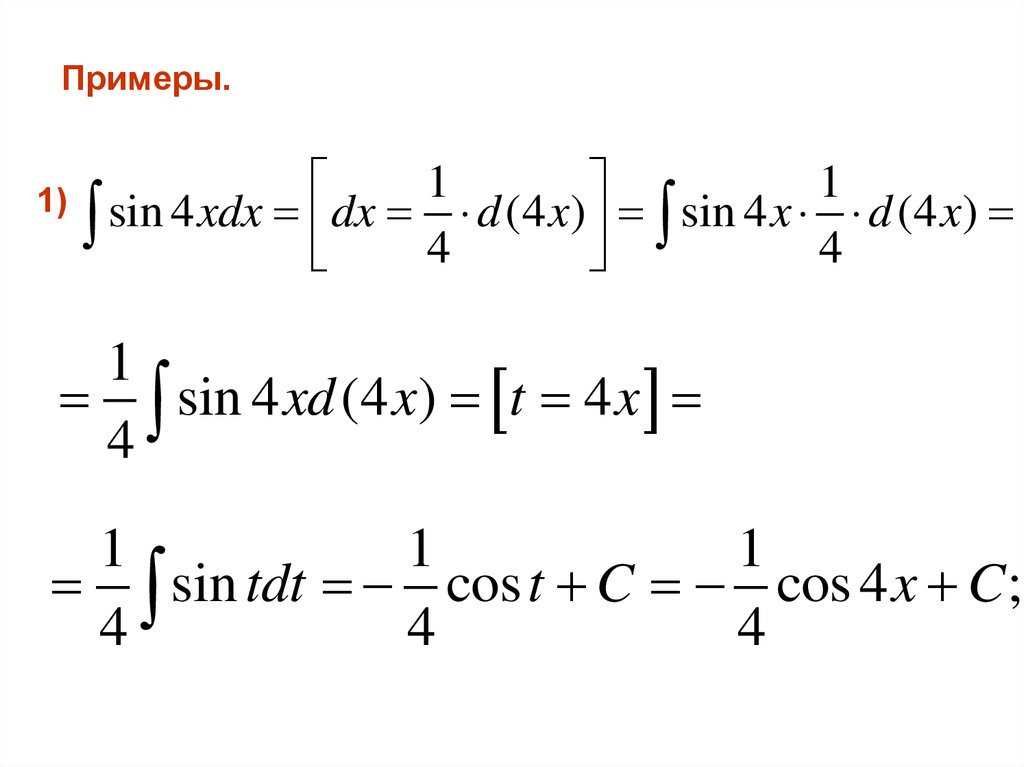


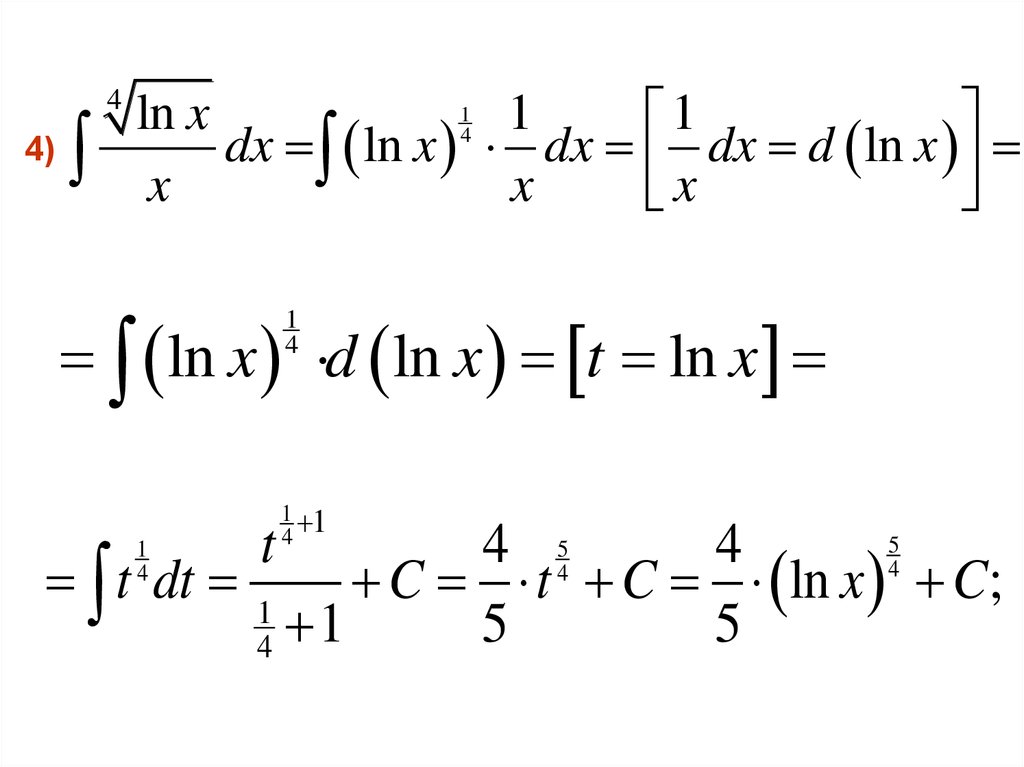




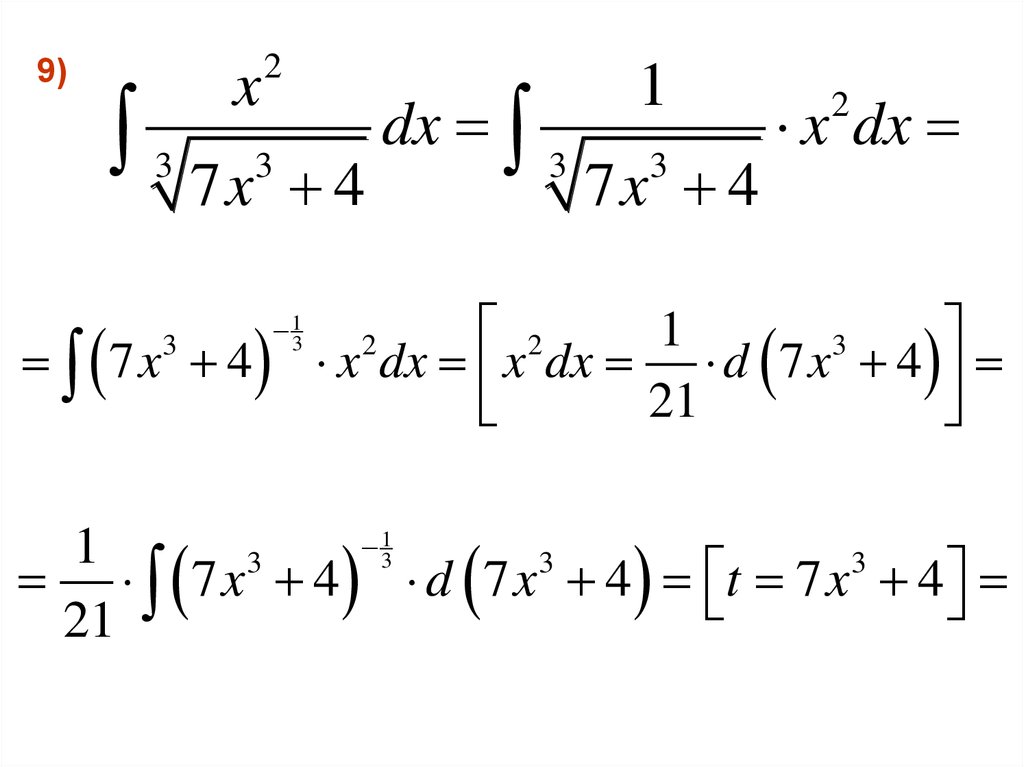
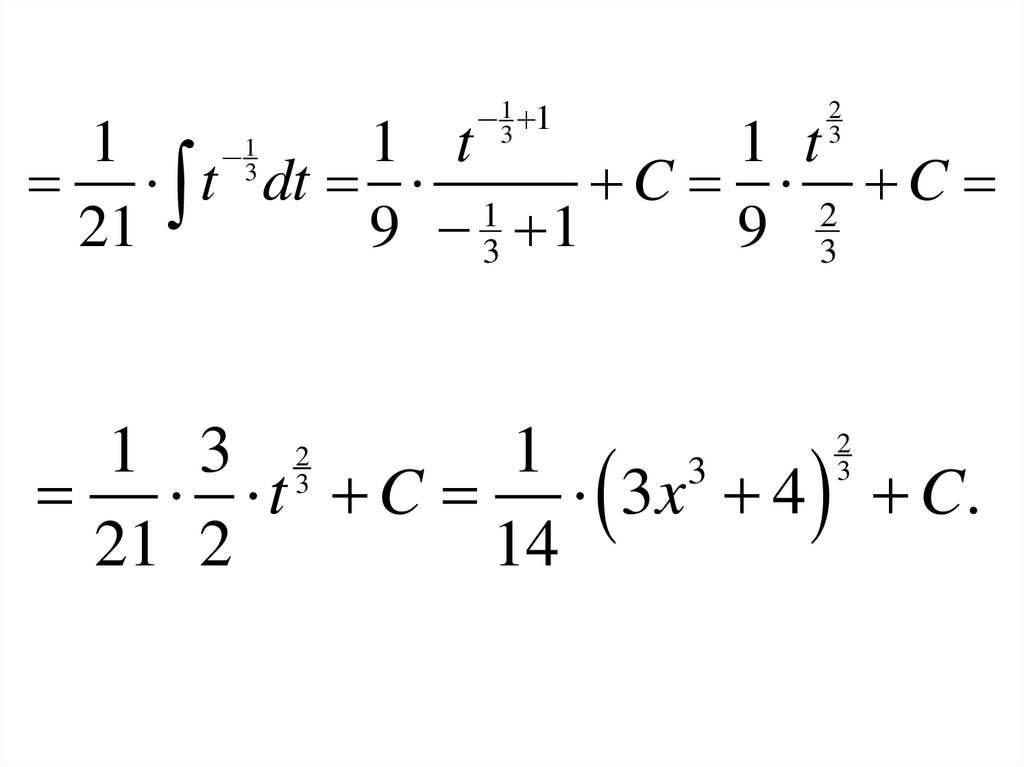




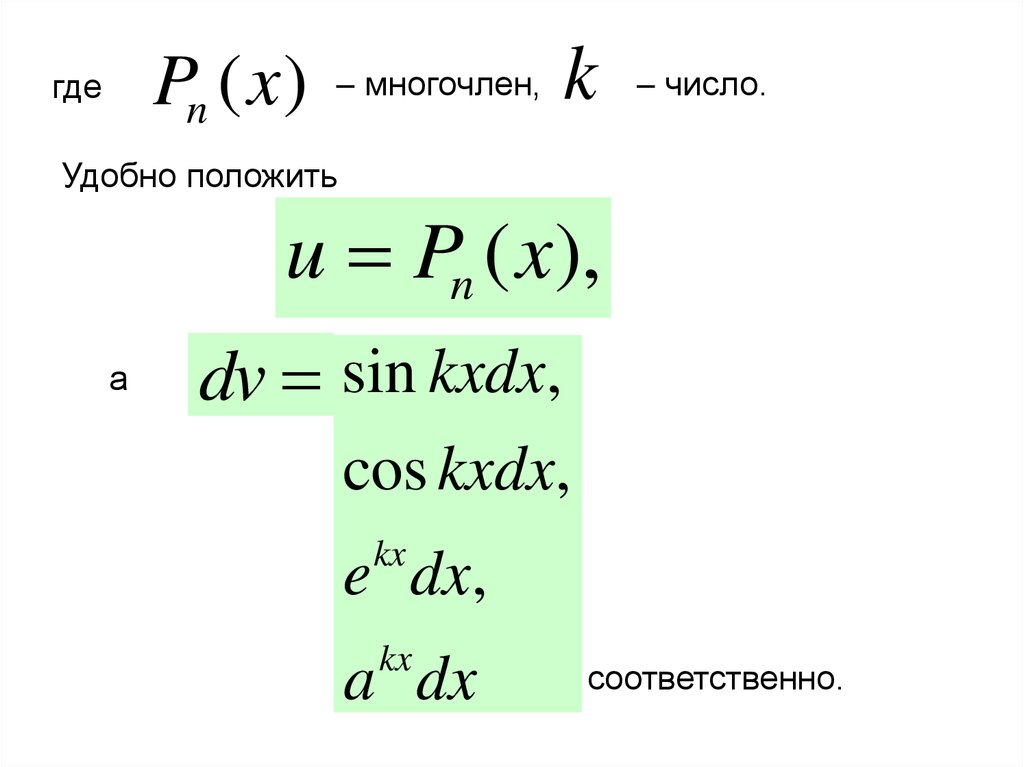




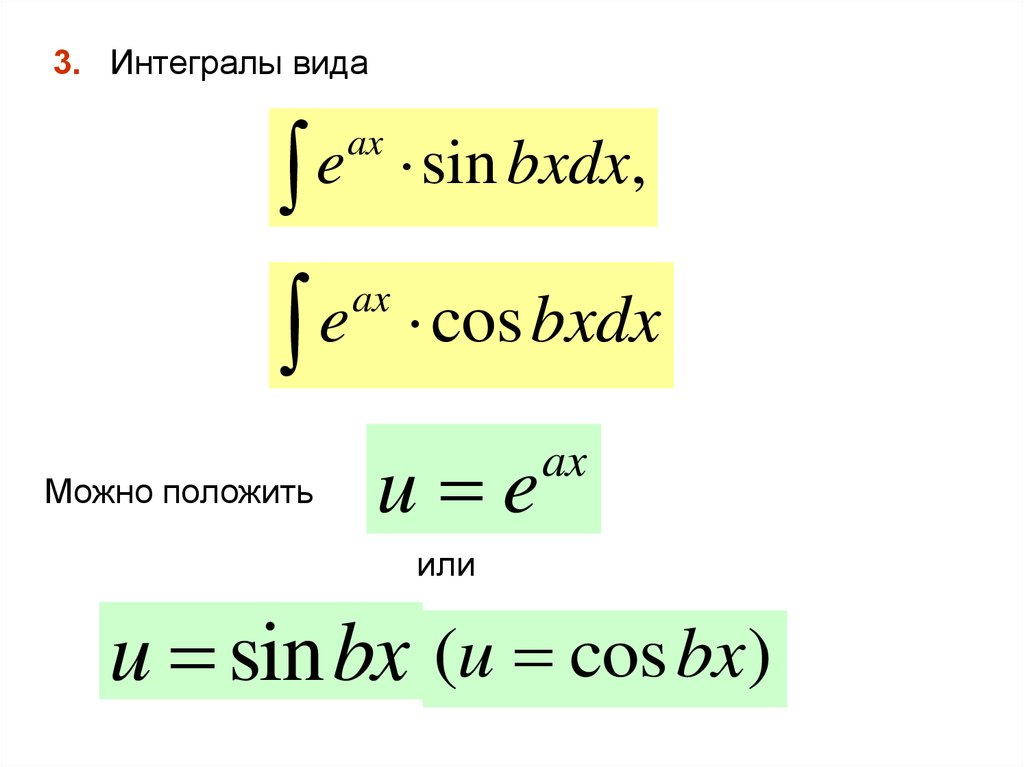
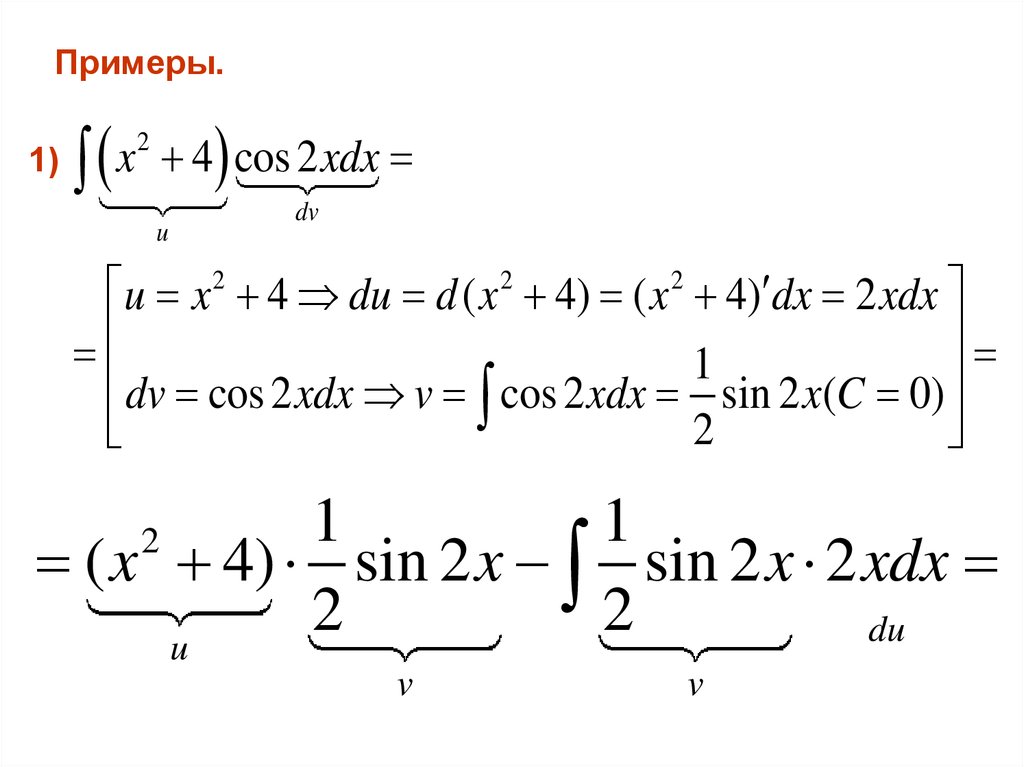


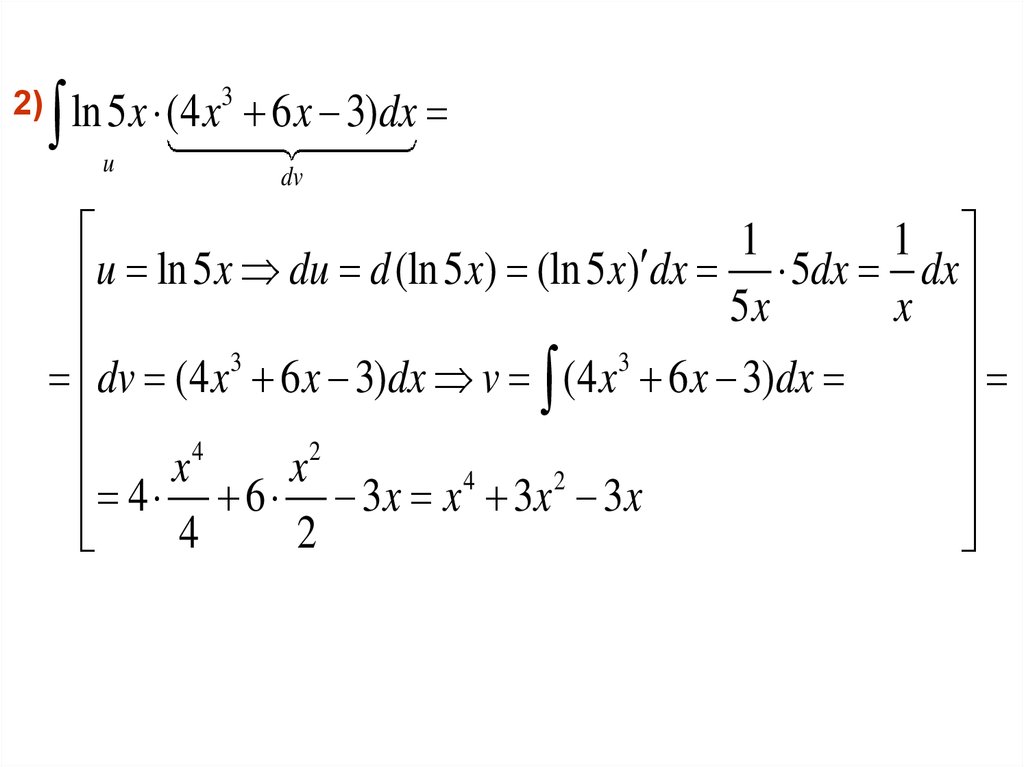









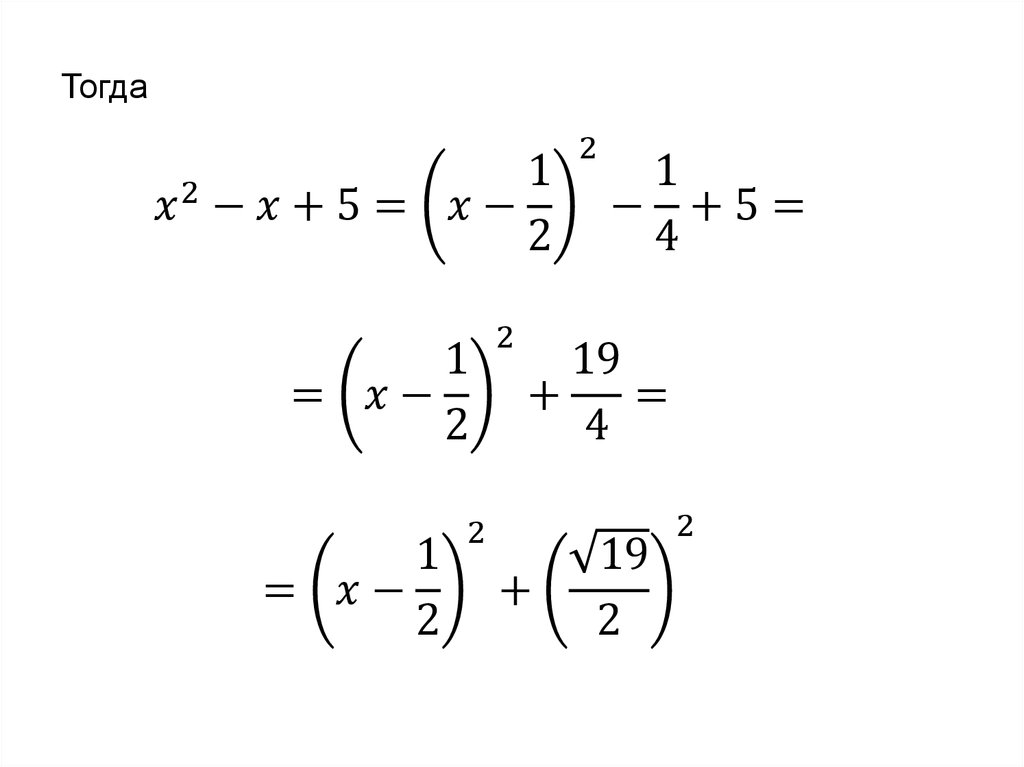



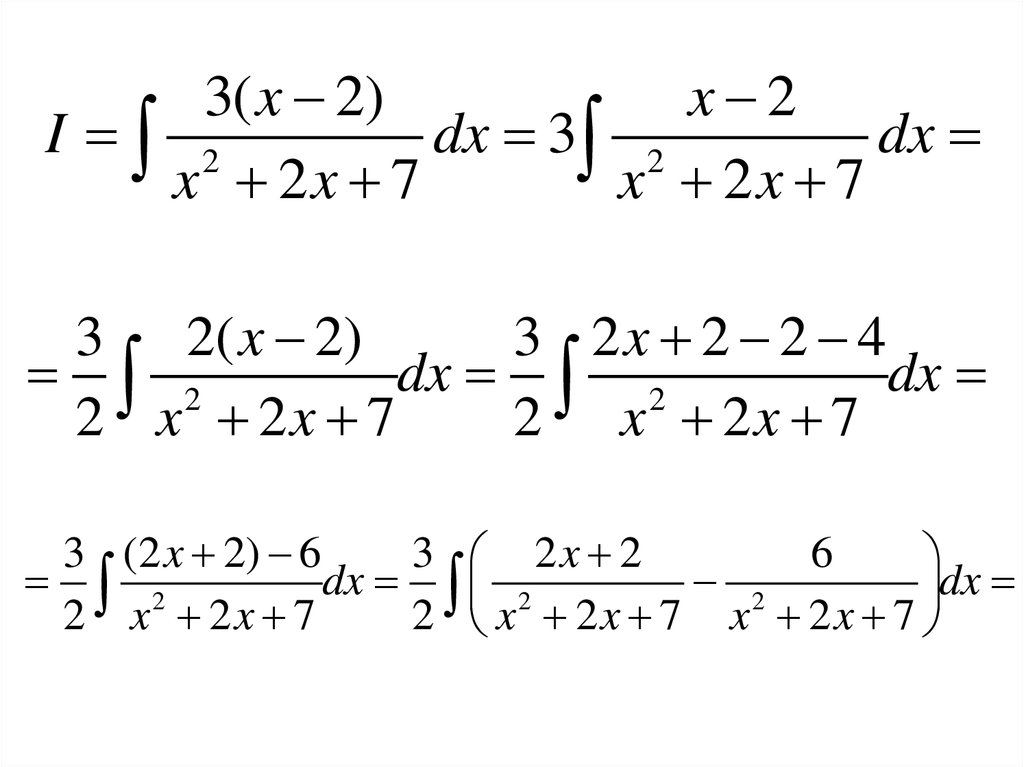

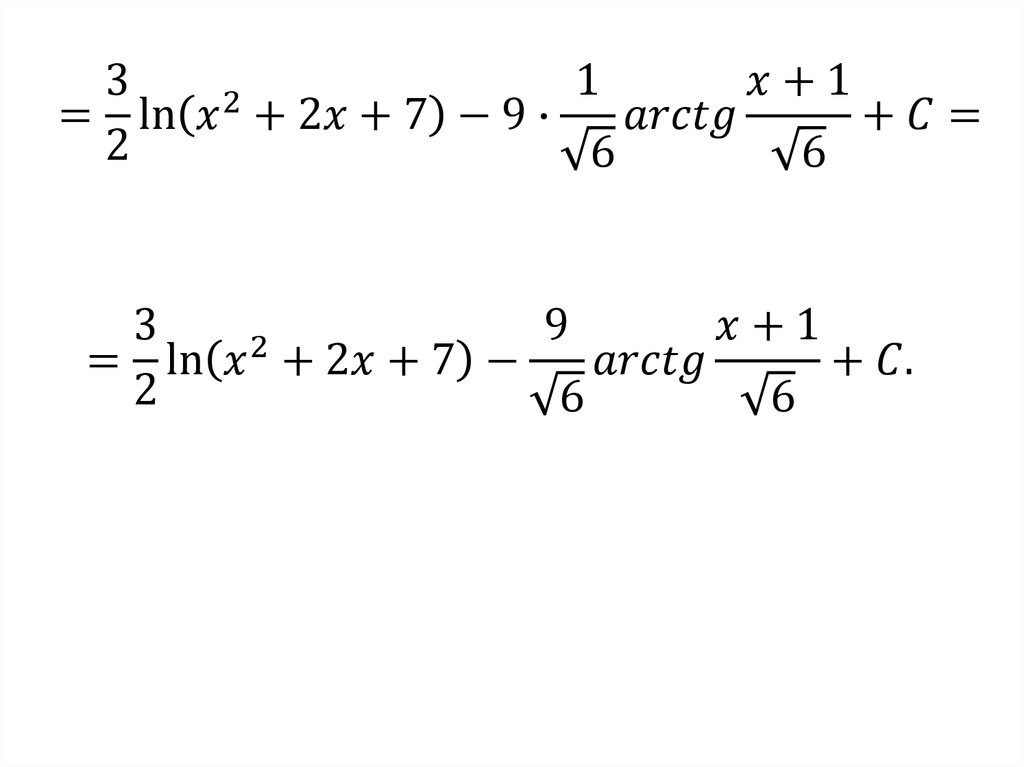









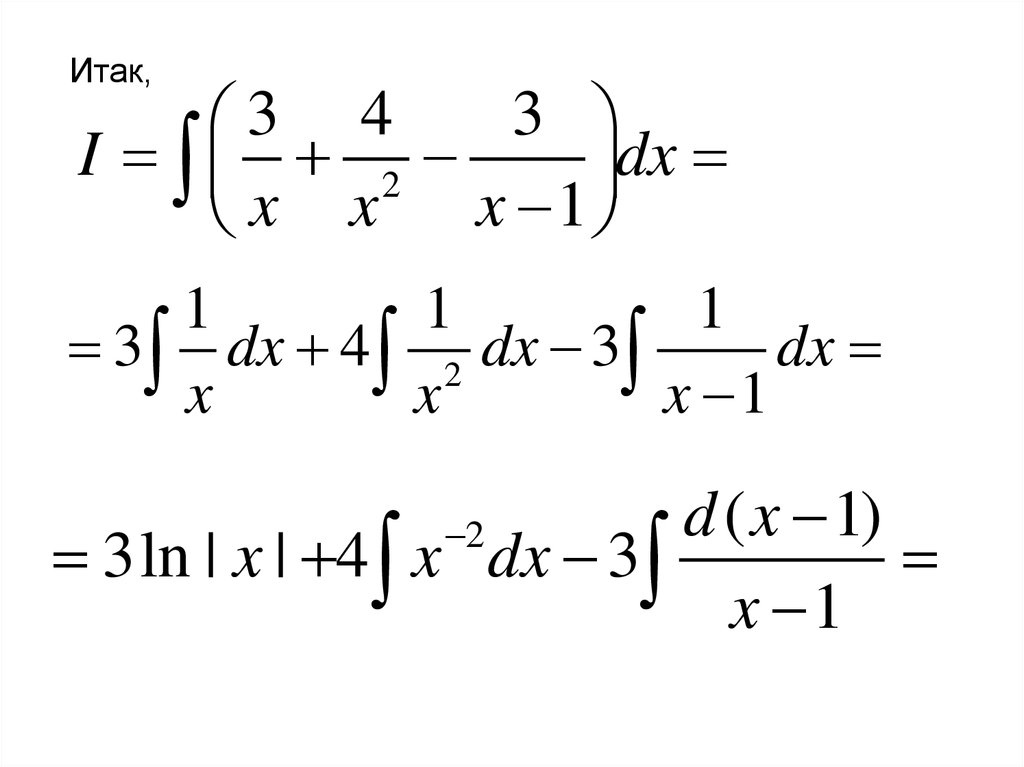
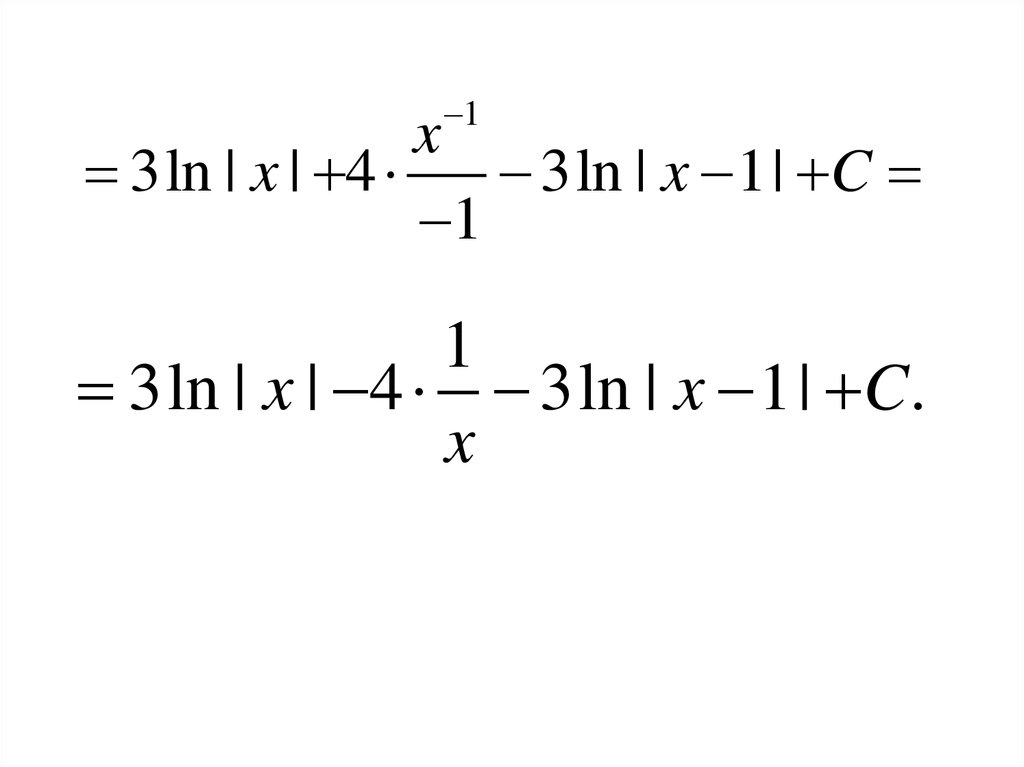

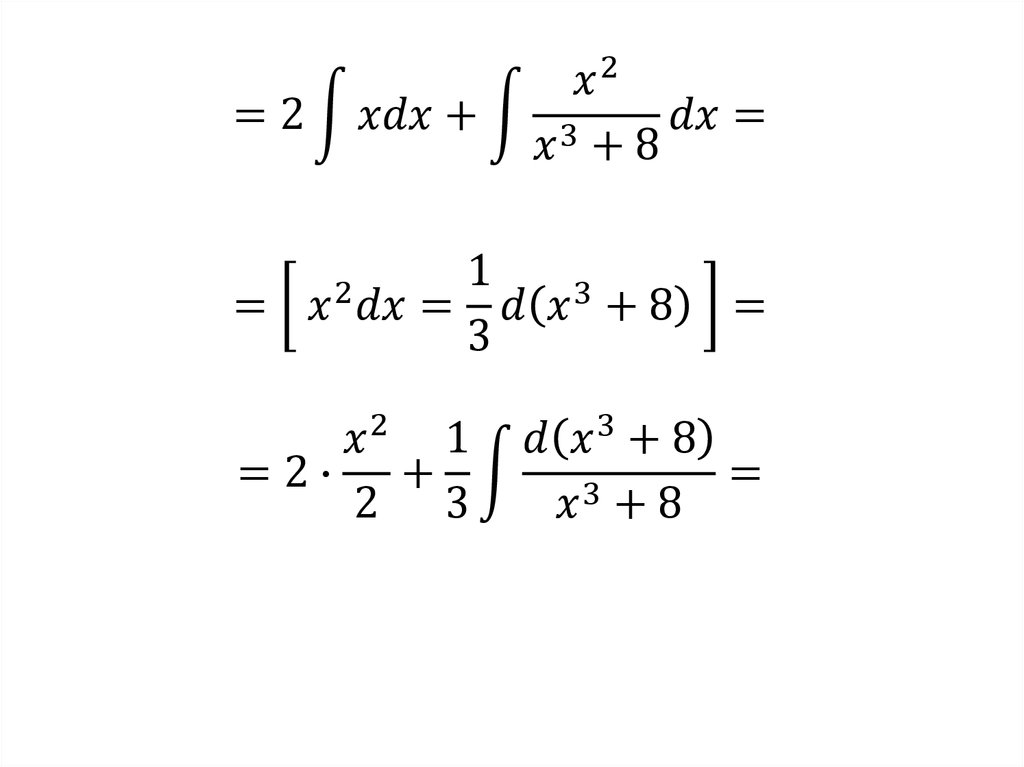

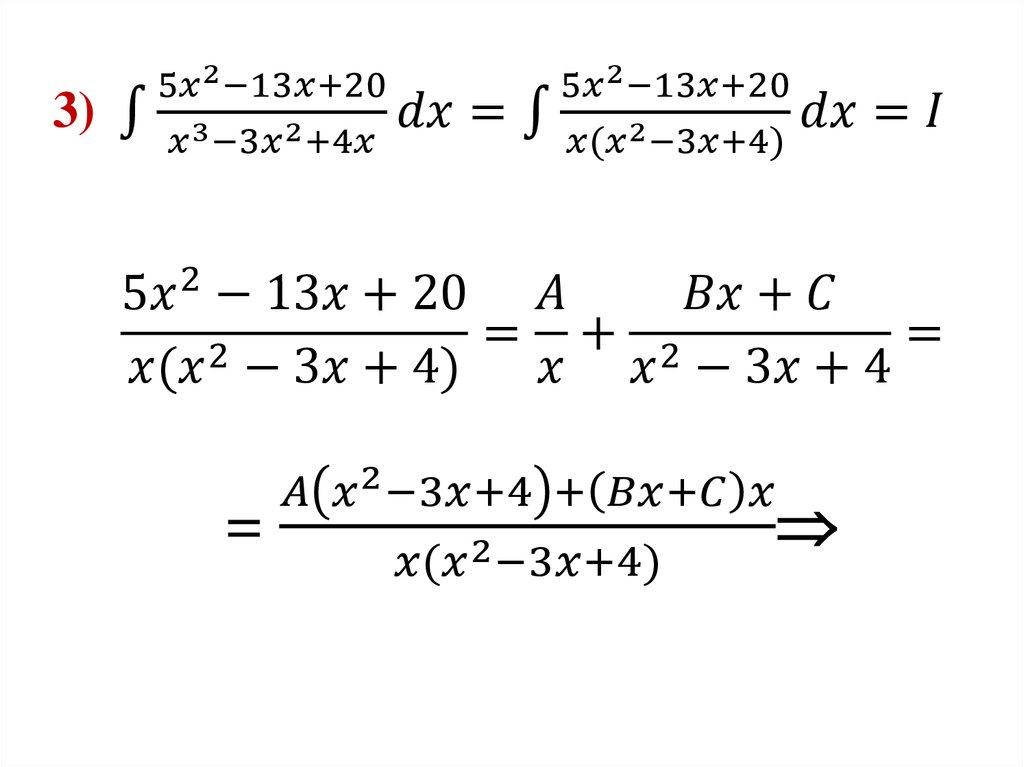
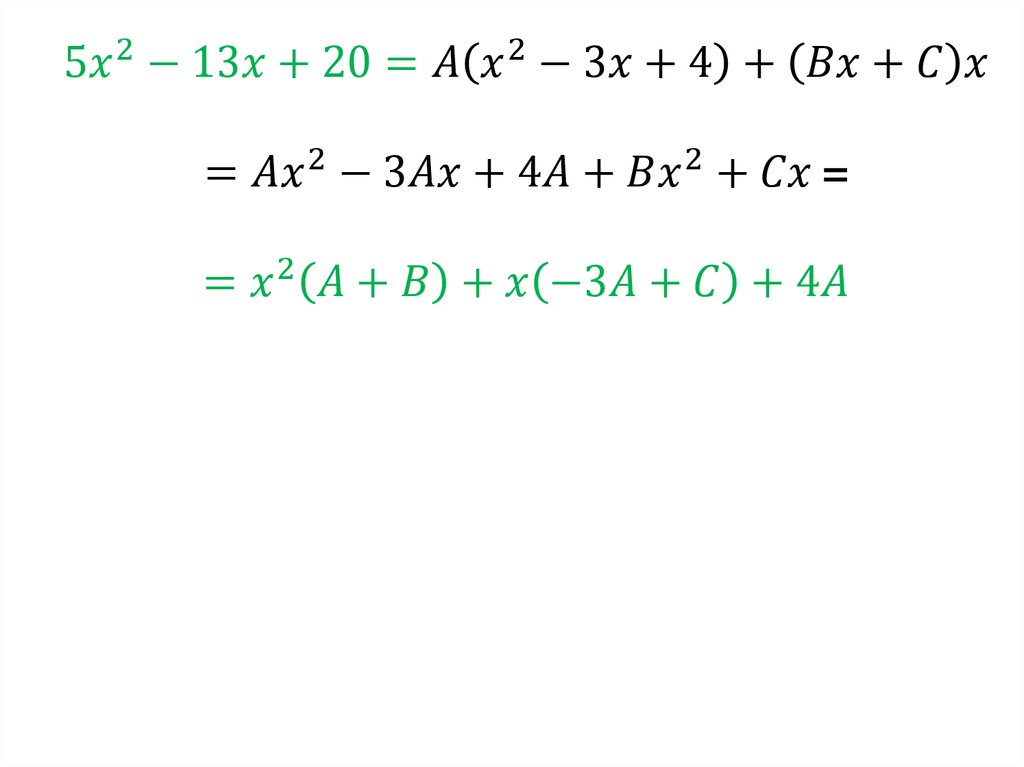


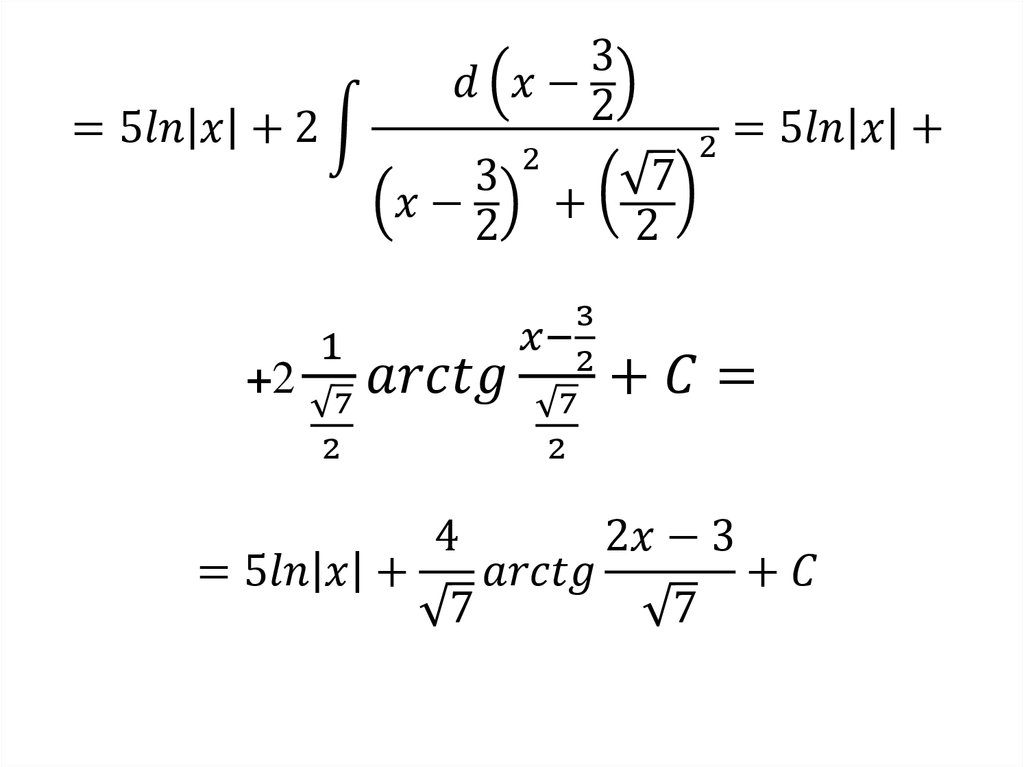


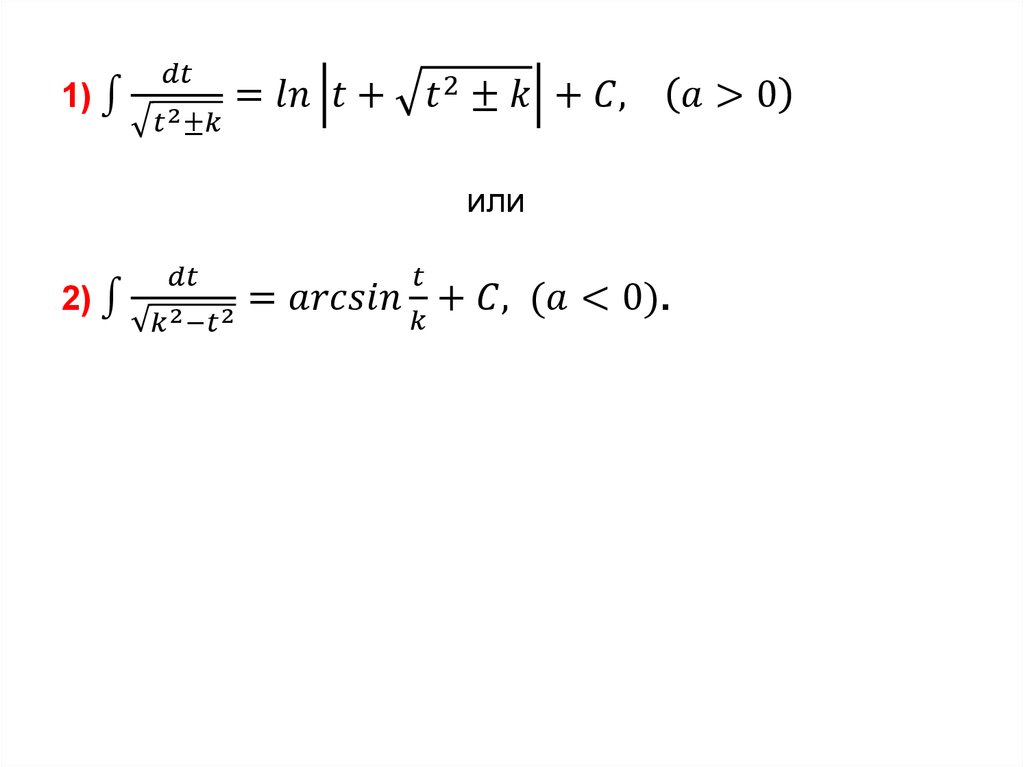




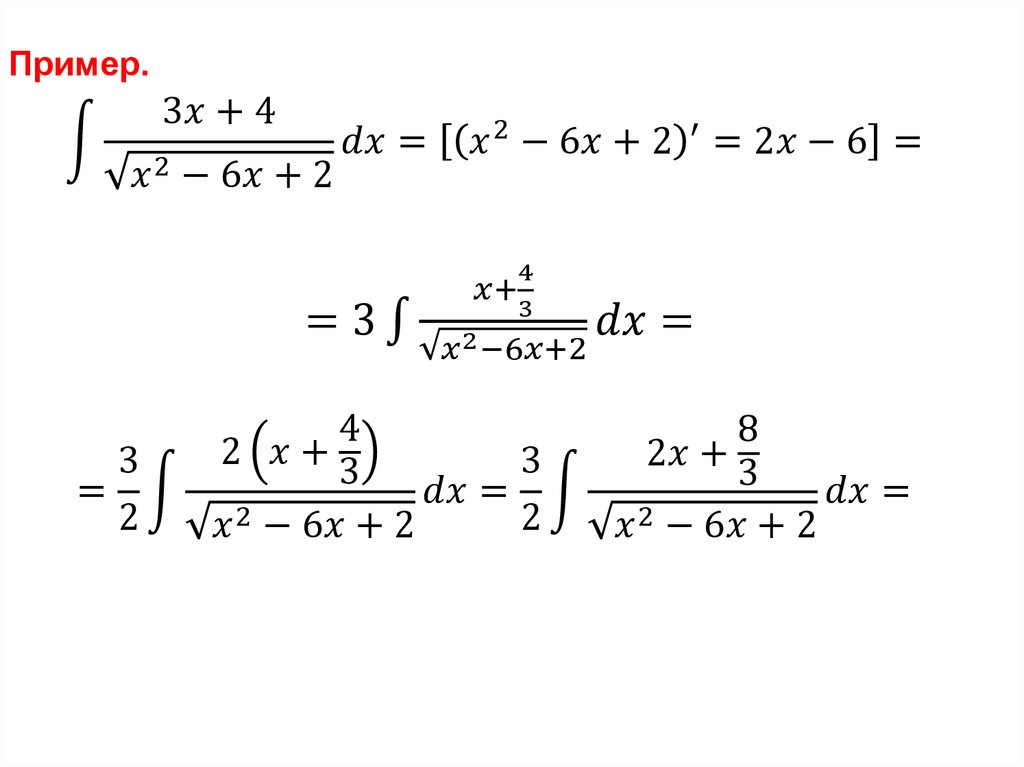
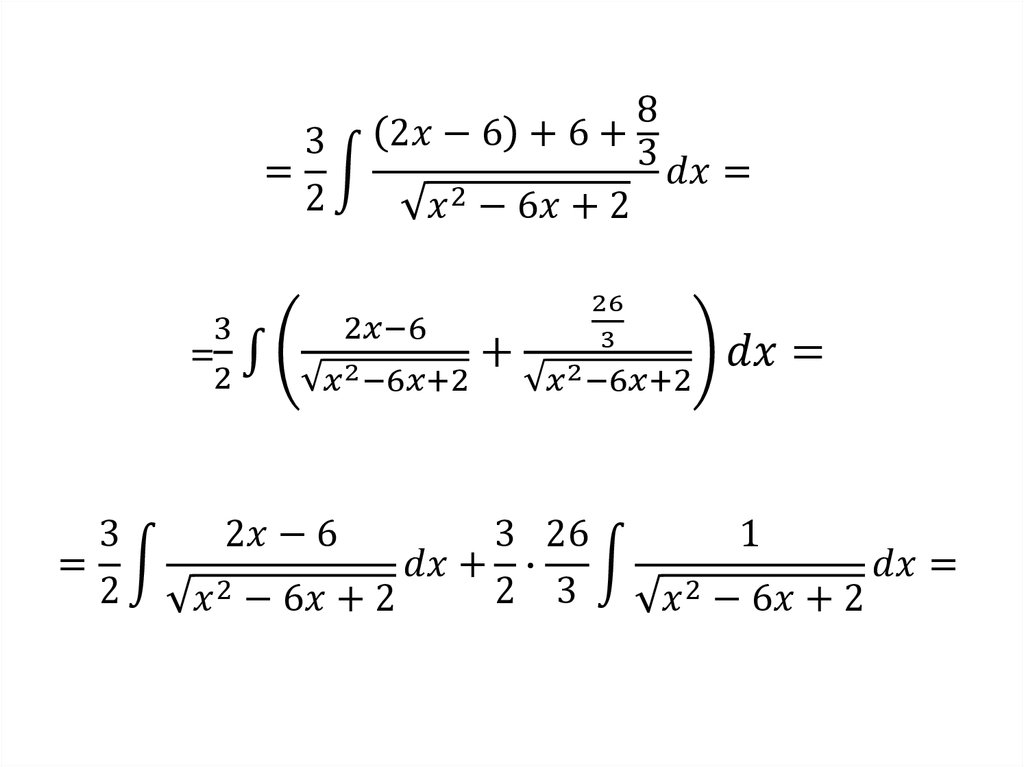
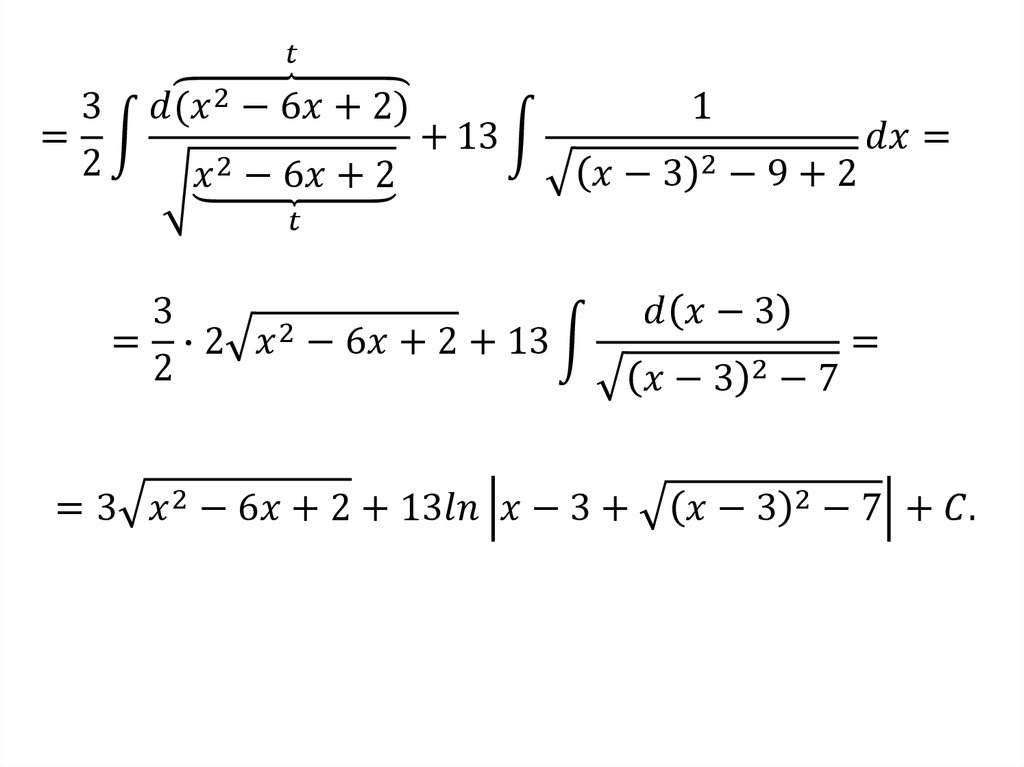


















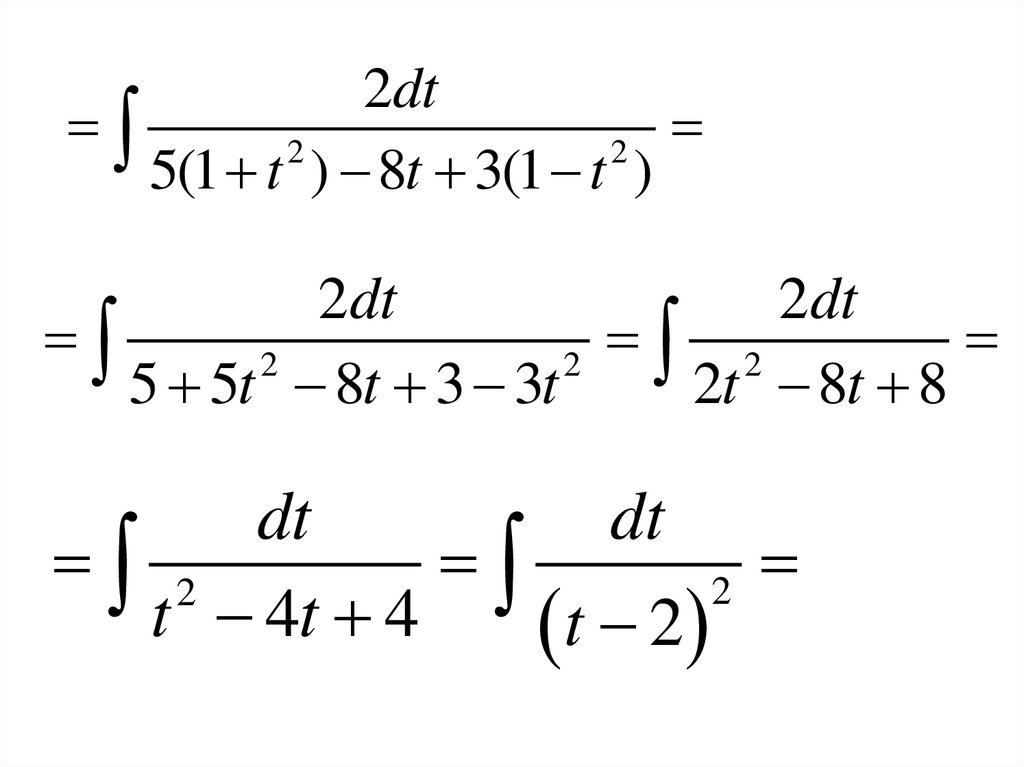
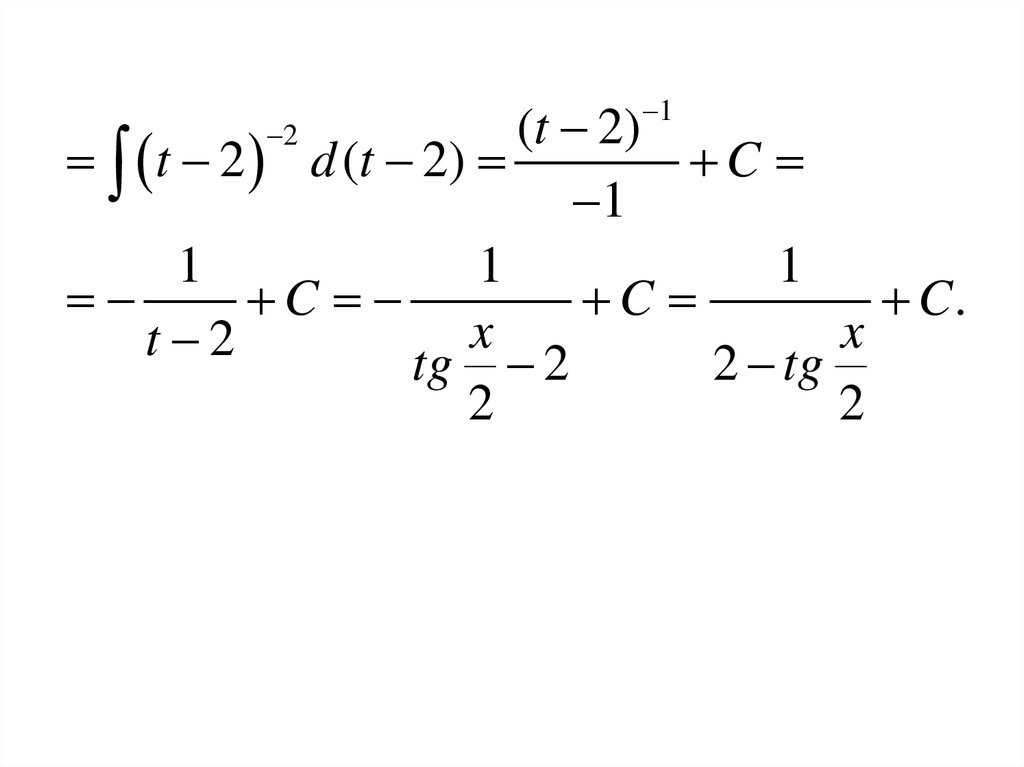


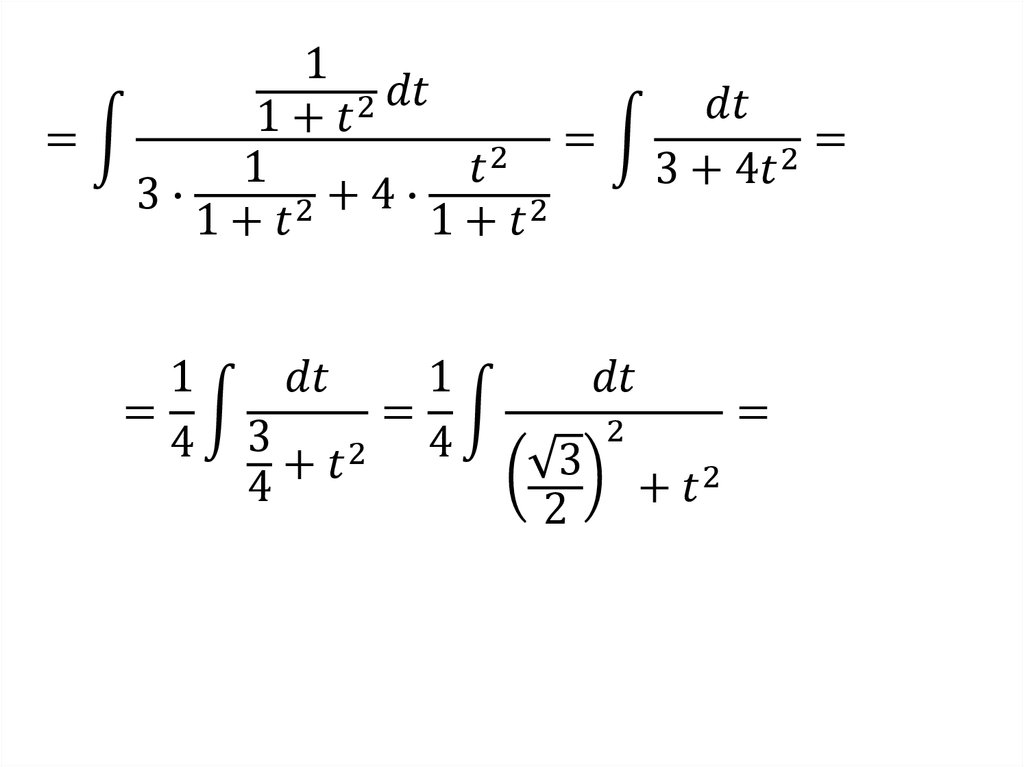

 Математика
Математика








