Похожие презентации:
Основы теории вероятностей и математической статистики
1.
2. Заключительное повторение по теме «Основы теории вероятностей и математической статистики»
Зачетный урок15 июня 2007 года
3. Таблица готовности по пятибалльной шкале
• 5 баллов – хочу знать, могу знать,интересно знать, делать, решать;
• 4 балла – я готов к работе;
• 3 балла – я не очень хорошо себя
чувствую, мне не все удается, я устаю
на уроке, я не понимаю материал, мне
нужна помощь.
4. Решение задач
ФОРМУЛА БЕРНУЛЛИВероятность того, что в n независимых
испытаниях «успех» наступит ровно m раз,
равна
где p – вероятность «успеха» в каждом
испытании, а q = 1 – p,
и m = 0, 1, 2, …, n.
5. Якоб Бернулли (1654 – 1705)
6.
Авторство формулы принадлежитизвестному швейцарскому математику Якову
Бернулли.
Он и его брат Иоганн придерживались
разных правил в математике.
Жесткие научные споры стимулировали
их творчество. Яков доказал частный случай
закона больших чисел, Иоганн многого
добился в теоретической механике и
математическом анализе, сын Иоганна
Даниил, работая в Петербурге занимался
математической статистикой.
7.
Задача № 1.Пассажиру, путешествующему в купейном вагоне,
удобно, если все его попутчики – лица того же пола,
что и он. Сколько процентов от таких пассажиров в
стране испытывают удобства?
Дано:
Испытание –
Событие А –
Событие В –
Найти:
8.
Задача № 1.Пассажиру, путешествующему в купейном вагоне,
удобно, если все его попутчики – лица того же пола,
что и он. Сколько процентов от таких пассажиров в
стране испытывают удобства?
Дано:
Испытание –
путешествие пассажира в купейном вагоне.
Событие А –
Событие В –
Найти:
9.
Задача № 1.Пассажиру, путешествующему в купейном вагоне,
удобно, если все его попутчики – лица того же пола,
что и он. Сколько процентов от таких пассажиров в
стране испытывают удобства?
Дано:
Испытание –
путешествие пассажира в купейном вагоне.
Событие А –
лицо мужского пола
Событие В –
Найти:
10.
Задача № 1.Пассажиру, путешествующему в купейном вагоне,
удобно, если все его попутчики – лица того же пола,
что и он. Сколько процентов от таких пассажиров в
стране испытывают удобства?
Дано:
Испытание –
путешествие пассажира в купейном вагоне.
Событие А –
лицо мужского пола
Событие В –
путешествовать удобно
Найти:
11.
Задача № 1.Пассажиру, путешествующему в купейном вагоне,
удобно, если все его попутчики – лица того же пола,
что и он. Сколько процентов от таких пассажиров в
стране испытывают удобства?
Дано:
Испытание –
путешествие пассажира в купейном вагоне.
Событие А –
лицо мужского пола
Событие В –
Найти:
путешествовать удобно
P(B)
12. Формула Пуассона
• λ – параметр, равен – np• e – экспонента
• m – число «успехов»
13. Сименон Дени Пуассон (1781 – 1841)
14.
• Закон, сформулированный Пуассоном, носитназвание закона редких событий. Когда сын
нотариуса Сименон Дени Пуассон (1781 – 1841)
выбирал свой путь – медицина или математика, – то
в дело вмешалась судьба. Первый и единственный
его пациент умер при кровопускании.
• Редкий «чистый» математик интересуется
практической стороной решаемых задач. Но Пуассон
был разносторонним ученым и человеком. Ему
принадлежат результаты в теории упругости,
атмосферного электричества, распространения волн
в бассейне, отклонения артиллерийских снарядов,
движения планет, вероятности уголовных приговоров
и азартных игр.
15.
– Известно, что в законе Пуассона математическоеожидание числа появлений события А (NA) равно
дисперсии этой величины.
М(NA) = D(NA) = λ.
С другой стороны, если какая-то случайная величина имеет
некоторую физическую размерность (например, измерена в
сантиметрах), то ее математическое ожидание имеет ту же
размерность, а дисперсия – квадрат этой размерности.
Как же тогда объяснить равенство
математического ожидания и дисперсии в законе
Пуассона?
16.
Задача № 2.Опытный врач ставит сто диагнозов в месяц, ошибаясь, в
среднем, два раза в месяц. Верно ли, что за 200 месяцев
работы таких месяцев, когда он ошибся два раза,
наберется больше, чем месяцев, когда он ошибся по
одному разу?
Дано: испытание – ________________________________
Событие А – _____________________________________
n = _____________________________________________
M (Na) = ________________________________________
Событие В – врач ошибся __________ в месяц – m1 = __
Событие С – врач ошибся __________ в месяц – m2 = __
2) Испытание – ___________________________________
N = _____________________________________________
Найти: 1) P100(1), NB, 2) P100(2 ), NC , 3) сравнить NB и NC.
17.
Задача № 2.Опытный врач ставит сто диагнозов в месяц, ошибаясь, в
среднем, два раза в месяц. Верно ли, что за 200 месяцев
работы таких месяцев, когда он ошибся два раза,
наберется больше, чем месяцев, когда он ошибся по
одному разу?
Дано: испытание – постановка диагноза
Событие А – _____________________________________
n = _____________________________________________
M (Na) = ________________________________________
Событие В – врач ошибся __________ в месяц – m1 = __
Событие С – врач ошибся __________ в месяц – m2 = __
2) Испытание – ___________________________________
N = _____________________________________________
Найти: 1) P100(1), NB, 2) P100(2 ), NC , 3) сравнить NB и NC.
18.
Задача № 2.Опытный врач ставит сто диагнозов в месяц, ошибаясь, в
среднем, два раза в месяц. Верно ли, что за 200 месяцев
работы таких месяцев, когда он ошибся два раза,
наберется больше, чем месяцев, когда он ошибся по
одному разу?
Дано: испытание – постановка диагноза
Событие А – диагноз ошибочный
n = _____________________________________________
M (Na) = _________________________________________
Событие В – врач ошибся __________ в месяц – m1 = __
Событие С – врач ошибся __________ в месяц – m2 = __
2) Испытание – ___________________________________
N = _____________________________________________
Найти: 1) P100(1), NB, 2) P100(2 ), NC , 3) сравнить NB и NC.
19.
Задача № 2.Опытный врач ставит сто диагнозов в месяц, ошибаясь, в
среднем, два раза в месяц. Верно ли, что за 200 месяцев
работы таких месяцев, когда он ошибся два раза,
наберется больше, чем месяцев, когда он ошибся по
одному разу?
Дано: испытание – постановка диагноза
Событие А – диагноз ошибочный
n = 100 – число диагнозов
M (Na) = _________________________________________
Событие В – врач ошибся __________ в месяц – m1 = __
Событие С – врач ошибся __________ в месяц – m2 = __
2) Испытание – ___________________________________
N = _____________________________________________
Найти: 1) P100(1), NB, 2) P100(2 ), NC , 3) сравнить NB и NC.
20.
Задача № 2.Опытный врач ставит сто диагнозов в месяц, ошибаясь, в
среднем, два раза в месяц. Верно ли, что за 200 месяцев
работы таких месяцев, когда он ошибся два раза,
наберется больше, чем месяцев, когда он ошибся по
одному разу?
Дано: испытание – постановка диагноза
Событие А – диагноз ошибочный
n = 100 – число диагнозов
M (Na) = 2 – среднее число ошибочных диагнозов
Событие В – врач ошибся __________ в месяц – m1 = __
Событие С – врач ошибся __________ в месяц – m2 = __
2) Испытание – ___________________________________
N = _____________________________________________
Найти: 1) P100(1), NB, 2) P100(2 ), NC , 3) сравнить NB и NC.
21.
Задача № 2.Опытный врач ставит сто диагнозов в месяц, ошибаясь, в
среднем, два раза в месяц. Верно ли, что за 200 месяцев
работы таких месяцев, когда он ошибся два раза,
наберется больше, чем месяцев, когда он ошибся по
одному разу?
Дано: испытание – постановка диагноза
Событие А – диагноз ошибочный
n = 100 – число диагнозов
M (Na) = 2 – среднее число ошибочных диагнозов
Событие В – врач ошибся один раз в месяц – m1 = 1
Событие С – врач ошибся __________ в месяц – m2 = __
2) Испытание – ___________________________________
N = _____________________________________________
Найти: 1) P100(1), NB, 2) P100(2 ), NC , 3) сравнить NB и NC.
22.
Задача № 2.Опытный врач ставит сто диагнозов в месяц, ошибаясь, в
среднем, два раза в месяц. Верно ли, что за 200 месяцев
работы таких месяцев, когда он ошибся два раза,
наберется больше, чем месяцев, когда он ошибся по
одному разу?
Дано: испытание – постановка диагноза
Событие А – диагноз ошибочный
n = 100 – число диагнозов
M (Na) = 2 – среднее число ошибочных диагнозов
Событие В – врач ошибся один раз в месяц – m1 = 1
Событие С – врач ошибся два раза в месяц – m2 = 2
2) Испытание – ___________________________________
N = _____________________________________________
Найти: 1) P100(1), NB, 2) P100(2 ), NC , 3) сравнить NB и NC.
23.
Задача № 2.Опытный врач ставит сто диагнозов в месяц, ошибаясь, в
среднем, два раза в месяц. Верно ли, что за 200 месяцев
работы таких месяцев, когда он ошибся два раза,
наберется больше, чем месяцев, когда он ошибся по
одному разу?
Дано: испытание – постановка диагноза
Событие А – диагноз ошибочный
n = 100 – число диагнозов
M (Na) = 2 – среднее число ошибочных диагнозов
Событие В – врач ошибся один раз в месяц – m1 = 1
Событие С – врач ошибся два раза в месяц – m2 = 2
2) Испытание – месяц работы
N = _____________________________________________
Найти: 1) P100(1), NB, 2) P100(2 ), NC , 3) сравнить NB и NC.
24.
Задача № 2.Опытный врач ставит сто диагнозов в месяц, ошибаясь, в
среднем, два раза в месяц. Верно ли, что за 200 месяцев
работы таких месяцев, когда он ошибся два раза,
наберется больше, чем месяцев, когда он ошибся по
одному разу?
Дано: испытание – постановка диагноза
Событие А – диагноз ошибочный
n = 100 – число диагнозов
M (Na) = 2 – среднее число ошибочных диагнозов
Событие В – врач ошибся один раз в месяц – m1 = 1
Событие С – врач ошибся два раза в месяц – m2 = 2
2) Испытание – месяц работы
N = 200 – число независимых испытаний
Найти: 1) P100(1), NB, 2) P100(2 ), NC , 3) сравнить NB и NC.
25. Функция Лапласа
Вероятность того, что событие Апоявится в n независимых испытаниях
m раз равна
26. Функция Лапласа
Вероятность того, что событие Апоявится в n независимых испытаниях от
k1 до k2 раз равна
где х' = (k1 — nр) /
и х'' = (k2 — nр) /
27. Пьер Лаплас (1749 – 1827)
28.
• Искусство и теология, древние языки и литература,физика и космология, математика и прикладные
исследования – решительно все интересовало Пьера
Лапласа (1749 – 1827). Он оставил глубокий след и в
основах теории вероятностей. Величие ученого
причудливо сочеталось в Лапласе с политической
эквилибристикой. Лаплас сначала был на стороне
республиканцев, затем стал министром внутренних
дел у Бонапарта, потом получил титулы пэра и
маркиза от новых Бурбонов. Функцию распределения
он исследовал в те времена, когда Наполеон
предпринял свой поход на Россию.
29.
• Интегральная функция Лапласа позволяетвычислять вероятности биномиального
распределения при достаточно большой
вероятности «успеха». С другой стороны, эта
функция используется для вычислений
вероятностей нормального распределения
непрерывной случайной величины, связывая,
тем самым теорию вероятностей и
математическую статистику.
30.
Задача № 3Вероятность рождения мальчика равна 0,515. Найти
вероятность того, что из 200 родившихся детей
мальчиков и девочек окажется поровну.
Дано:
Испытание – _______________________________________
N = ________________________________________________
Событие А – ________________________________________
P(A) = ______________________________________________
Событие В – ________________________________________
___________________________________________________
Найти: P (B)
31.
Задача № 3Вероятность рождения мальчика равна 0,515. Найти
вероятность того, что из 200 родившихся детей
мальчиков и девочек окажется поровну.
Дано:
Испытание – рождение ребенка,
N = ________________________________________________
Событие А – ________________________________________
P(A) = ______________________________________________
Событие В – ________________________________________
___________________________________________________
Найти: P (B)
32.
Задача № 3Вероятность рождения мальчика равна 0,515. Найти
вероятность того, что из 200 родившихся детей
мальчиков и девочек окажется поровну.
Дано:
Испытание – рождение ребенка,
N = 200 – число родившихся детей,
Событие А – ________________________________________
P(A) = ______________________________________________
Событие В – ________________________________________
___________________________________________________
Найти: P (B)
33.
Задача № 3Вероятность рождения мальчика равна 0,515. Найти
вероятность того, что из 200 родившихся детей
мальчиков и девочек окажется поровну.
Дано:
Испытание – рождение ребенка,
N = 200 – число родившихся детей,
Событие А – рождение мальчика,
P(A) = ______________________________________________
Событие В – ________________________________________
___________________________________________________
Найти: P (B)
34.
Задача № 3Вероятность рождения мальчика равна 0,515. Найти
вероятность того, что из 200 родившихся детей
мальчиков и девочек окажется поровну.
Дано:
Испытание – рождение ребенка,
N = 200 – число родившихся детей,
Событие А – рождение мальчика,
P(A) = 0,515 – вероятность рождения мальчика,
Событие В – ________________________________________
___________________________________________________
Найти: P (B)
35.
Задача № 3Вероятность рождения мальчика равна 0,515. Найти
вероятность того, что из 200 родившихся детей
мальчиков и девочек окажется поровну.
Дано:
Испытание – рождение ребенка,
N = 200 – число родившихся детей,
Событие А – рождение мальчика,
P(A) = 0,515 – вероятность рождения мальчика,
Событие В – из 200 родившихся детей мальчиков и девочек
окажется поровну
Найти: P (B)
36.
Решение:Рассмотрим событие B – ______________________________
___________________________________________________
По условию дана схема _______________________________
1) число испытаний __________________________________
2) каждое испытание приводит к ________________________
___________________________________________________
3) вероятность «успеха» ______________________________
4) испытания ________________________________________
Известно по условию задачи, что вероятность рождения
мальчика равна __________
Число испытаний _________________, проверим значение
n · p: ______________________________________________
следовательно ______________________________________
___________________________________________________
37.
Решение:Рассмотрим событие B – из 200т детей мальчиков и
девочек родится поровну.
По условию дана схема _______________________________
1) число испытаний __________________________________
2) каждое испытание приводит к ________________________
___________________________________________________
3) вероятность «успеха» ______________________________
4) испытания ________________________________________
Известно по условию задачи, что вероятность рождения
мальчика равна __________
Число испытаний _________________, проверим значение
n · p: ______________________________________________
следовательно ______________________________________
___________________________________________________
38.
Решение:Рассмотрим событие B – из 200т детей мальчиков и
девочек родится поровну.
По условию дана схема независимых испытаний Бернулли:
1) число испытаний __________________________________
2) каждое испытание приводит к ________________________
___________________________________________________
3) вероятность «успеха» ______________________________
4) испытания ________________________________________
Известно по условию задачи, что вероятность рождения
мальчика равна __________
Число испытаний _________________, проверим значение
n · p: ______________________________________________
следовательно ______________________________________
___________________________________________________
39.
Решение:Рассмотрим событие B – из 200т детей мальчиков и
девочек родится поровну.
По условию дана схема независимых испытаний Бернулли:
1) число испытаний конечно,
2) каждое испытание приводит к ________________________
___________________________________________________
3) вероятность «успеха» ______________________________
4) испытания ________________________________________
Известно по условию задачи, что вероятность рождения
мальчика равна __________
Число испытаний _________________, проверим значение
n · p: ______________________________________________
следовательно ______________________________________
___________________________________________________
40.
Решение:Рассмотрим событие B – из 200т детей мальчиков и
девочек родится поровну.
По условию дана схема независимых испытаний Бернулли:
1) число испытаний конечно,
2) каждое испытание приводит к двум взаимно исключающим
исходам,
3) вероятность «успеха» ______________________________
4) испытания ________________________________________
Известно по условию задачи, что вероятность рождения
мальчика равна __________
Число испытаний _________________, проверим значение
n · p: ______________________________________________
следовательно ______________________________________
___________________________________________________
41.
Решение:Рассмотрим событие B – из 200т детей мальчиков и
девочек родится поровну.
По условию дана схема независимых испытаний Бернулли:
1) число испытаний конечно,
2) каждое испытание приводит к двум взаимно исключающим
исходам,
3) вероятность «успеха» во всех испытаниях одинаковая,
4) испытания ________________________________________
Известно по условию задачи, что вероятность рождения
мальчика равна __________
Число испытаний _________________, проверим значение
n · p: ______________________________________________
следовательно ______________________________________
___________________________________________________
42.
Решение:Рассмотрим событие B – из 200т детей мальчиков и
девочек родится поровну.
По условию дана схема независимых испытаний Бернулли:
1) число испытаний конечно,
2) каждое испытание приводит к двум взаимно исключающим
исходам,
3) вероятность «успеха» во всех испытаниях одинаковая,
4) испытания независимы.
Известно по условию задачи, что вероятность рождения
мальчика равна __________
Число испытаний _________________, проверим значение
n · p: ______________________________________________
следовательно ______________________________________
___________________________________________________
43.
Решение:Рассмотрим событие B – из 200т детей мальчиков и
девочек родится поровну.
По условию дана схема независимых испытаний Бернулли:
1) число испытаний конечно,
2) каждое испытание приводит к двум взаимно исключающим
исходам,
3) вероятность «успеха» во всех испытаниях одинаковая,
4) испытания независимы.
Известно по условию задачи, что вероятность рождения
мальчика равна 0,515.
Число испытаний _________________, проверим значение
n · p: ______________________________________________
следовательно ______________________________________
___________________________________________________
44.
Решение:Рассмотрим событие B – из 200т детей мальчиков и
девочек родится поровну.
По условию дана схема независимых испытаний Бернулли:
1) число испытаний конечно,
2) каждое испытание приводит к двум взаимно исключающим
исходам,
3) вероятность «успеха» во всех испытаниях одинаковая,
4) испытания независимы.
Известно по условию задачи, что вероятность рождения
мальчика равна 0,515.
Число испытаний достаточно велико, проверим значение
n · p: ______________________________________________
следовательно ______________________________________
___________________________________________________
45.
Решение:Рассмотрим событие B – из 200т детей мальчиков и
девочек родится поровну.
По условию дана схема независимых испытаний Бернулли:
1) число испытаний конечно,
2) каждое испытание приводит к двум взаимно исключающим
исходам,
3) вероятность «успеха» во всех испытаниях одинаковая,
4) испытания независимы.
Известно по условию задачи, что вероятность рождения
мальчика равна 0,515.
Число испытаний достаточно велико, проверим значение
n · p: n · p = 0.515 · 200 = 103 > 10,
следовательно ______________________________________
___________________________________________________
46.
Решение:Рассмотрим событие B – из 200т детей мальчиков и
девочек родится поровну.
По условию дана схема независимых испытаний Бернулли:
1) число испытаний конечно,
2) каждое испытание приводит к двум взаимно исключающим
исходам,
3) вероятность «успеха» во всех испытаниях одинаковая,
4) испытания независимы.
Известно по условию задачи, что вероятность рождения
мальчика равна 0,515.
Число испытаний достаточно велико, проверим значение
n · p: n · p = 0.515 · 200 = 103 > 10,
следовательно необходимо применить теорему
Муавра-Лапласа:
47.
По условию: n = ____, p = ____, q = 1 – p = _______Вычислим npq = _____________________________________
m – np = _____________, тогда u = ______________,
известно, что
По таблице 1 приложения стр. 330 [ учебник Калининой ]
находим
f(u) = ___________________________________
Подставим найденные значения в формулу Муавра-Лапласа
___________________________________________________
Ответ: ________________
48.
По условию: n = 200, p = 0.515, q = 1 – p = 0.485.Вычислим npq = _____________________________________
m – np = _____________, тогда u = ______________,
известно, что
По таблице 1 приложения стр. 330 [ учебник Калининой ]
находим
f(u) = ___________________________________
Подставим найденные значения в формулу Муавра-Лапласа
___________________________________________________
Ответ: ________________
49.
По условию: n = 200, p = 0.515, q = 1 – p = 0.485.Вычислим npq = 200 ∙ 0.515 ∙ 0.485 = 49.955,
m – np = _____________, тогда u = ______________,
известно, что
По таблице 1 приложения стр. 330 [ учебник Калининой ]
находим
f(u) = ___________________________________
Подставим найденные значения в формулу Муавра-Лапласа
___________________________________________________
Ответ: ________________
50.
По условию: n = 200, p = 0.515, q = 1 – p = 0.485.Вычислим npq = 200 ∙ 0.515 ∙ 0.485 = 49.955,
m – np = 100 – 103 = - 3,тогда
,
известно, что
По таблице 1 приложения стр. 330 [ учебник Калининой ]
находим
f(u) = ___________________________________
Подставим найденные значения в формулу Муавра-Лапласа
___________________________________________________
Ответ: ________________
51.
По условию: n = 200, p = 0.515, q = 1 – p = 0.485.Вычислим npq = 200 ∙ 0.515 ∙ 0.485 = 49.955,
m – np = 100 – 103 = - 3,тогда
,
известно, что
По таблице 1 приложения стр. 330 [ учебник Калининой ]
находим
Подставим найденные значения в формулу Муавра-Лапласа
___________________________________________________
Ответ: ________________
52.
По условию: n = 200, p = 0.515, q = 1 – p = 0.485.Вычислим npq = 200 ∙ 0.515 ∙ 0.485 = 49.955,
m – np = 100 – 103 = - 3,тогда
,
известно, что
По таблице 1 приложения стр. 330 [ учебник Калининой ]
находим
Подставим найденные значения в формулу Муавра-Лапласа
Ответ: Р( А) = 0,05.
53.
Задача № 4.Благодаря достижениям ботаники и химии яблоки в
райском саду растут на загляденье. Масса каждого яблока
X – нормальная случайная величина.
Откуда это известно? Конечно же, из большого опыта.
Давно установлено, что М(X) = 150 грамм, σ(X) = 10.
Первосортные лишь те яблоки, у которых X > 135 г.
Сколько процентов яблок в райском саду считается
яблоками первого сорта?
Дано: непрерывная случайная величина X – число
___________________, распределена по ______________
закону. М(X) = ____
Событие А – ________________________.
Найти: P(X > 135)
54.
Задача № 4.Благодаря достижениям ботаники и химии яблоки в
райском саду растут на загляденье. Масса каждого яблока
X – нормальная случайная величина.
Откуда это известно? Конечно же, из большого опыта.
Давно установлено, что М(X) = 150 грамм, σ(X) = 10.
Первосортные лишь те яблоки, у которых X > 135 г.
Сколько процентов яблок в райском саду считается
яблоками первого сорта?
Дано: непрерывная случайная величина X – число
граммов массы яблока, распределена по нормальному
закону. М(X) = ____
Событие А – ________________________.
Найти: P(X > 135)
55.
Задача № 4.Благодаря достижениям ботаники и химии яблоки в
райском саду растут на загляденье. Масса каждого яблока
X – нормальная случайная величина.
Откуда это известно? Конечно же, из большого опыта.
Давно установлено, что М(X) = 150 грамм, σ(X) = 10.
Первосортные лишь те яблоки, у которых X > 135 г.
Сколько процентов яблок в райском саду считается
яблоками первого сорта?
Дано: непрерывная случайная величина X – число
граммов массы яблока, распределена по нормальному
закону. М(X) = 150
Событие А – ________________________.
Найти: P(X > 135)
56.
Задача № 4.Благодаря достижениям ботаники и химии яблоки в
райском саду растут на загляденье. Масса каждого яблока
X – нормальная случайная величина.
Откуда это известно? Конечно же, из большого опыта.
Давно установлено, что М(X) = 150 грамм, σ(X) = 10.
Первосортные лишь те яблоки, у которых X > 135 г.
Сколько процентов яблок в райском саду считается
яблоками первого сорта?
Дано: непрерывная случайная величина X – число
граммов массы яблока, распределена по нормальному
закону. М(X) = 150
Событие А – яблоко первосортно.
Найти: P(X > 135)
57. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
fa = Na / N - формула частотыA-?
N a- ?
N-?
Как найти N a ?
Как найти N?
58.
Задача № 5.С утра сидит на озере любитель рыболов.
Он поймал сеткой поодиночке 99 рыб (выборка).
Пометив каждую рыбку краской, он выпустил их в озеро.
Через день он поймал 90 рыб и обнаружил среди них 9
меченых. Сколько примерно рыб в озере, то есть в
генеральной совокупности?
Дано:
генеральная совокупность объема NГ – ________________,
выборка объема nв = __ – число ________________,
испытание – ______________, N = ____
событие А – ______________________, Na = _
Найти: NГ
59.
Задача № 5.С утра сидит на озере любитель рыболов.
Он поймал сеткой поодиночке 99 рыб (выборка).
Пометив каждую рыбку краской, он выпустил их в озеро.
Через день он поймал 90 рыб и обнаружил среди них 9
меченых. Сколько примерно рыб в озере, то есть в
генеральной совокупности?
Дано:
генеральная совокупность объема NГ – число рыб в озере,
выборка объема nв = __ – число ________________,
испытание – ______________, N = ____
событие А – ______________________, Na = _
Найти: NГ
60.
Задача № 5.С утра сидит на озере любитель рыболов.
Он поймал сеткой поодиночке 99 рыб (выборка).
Пометив каждую рыбку краской, он выпустил их в озеро.
Через день он поймал 90 рыб и обнаружил среди них 9
меченых. Сколько примерно рыб в озере, то есть в
генеральной совокупности?
Дано:
генеральная совокупность объема NГ – число рыб в озере,
выборка объема nв = 99 – число пойманных рыб,
испытание – ______________, N = ____
событие А – ______________________, Na =
Найти: NГ
61.
Задача № 4.С утра сидит на озере любитель рыболов.
Он поймал сеткой поодиночке 99 рыб (выборка).
Пометив каждую рыбку краской, он выпустил их в озеро.
Через день он поймал 90 рыб и обнаружил среди них 9
меченых. Сколько примерно рыб в озере, то есть в
генеральной совокупности?
Дано:
генеральная совокупность объема NГ – число рыб в озере,
выборка объема nв = 99 – число пойманных рыб,
испытание – поймать 1 рыбку, N = 90
событие А – ______________________, Na =
Найти: NГ
62.
Задача № 4.С утра сидит на озере любитель рыболов.
Он поймал сеткой поодиночке 99 рыб (выборка).
Пометив каждую рыбку краской, он выпустил их в озеро.
Через день он поймал 90 рыб и обнаружил среди них 9
меченых. Сколько примерно рыб в озере, то есть в
генеральной совокупности?
Дано:
генеральная совокупность объема NГ – число рыб в озере,
выборка объема nв = 99 – число пойманных рыб,
испытание – поймать 1 рыбку, N = 90
событие А – поймать меченую рыбку, Na = 9
Найти: NГ
63. Из каких разделов состоит предмет теории вероятностей?
• Случайное событие• Случайные величины (дискретные и
непрерывные)
• Математическая статистика
64. Чем отличаются задачи первого и второго разделов?
• В теме «Случайное событие» вычисляютвероятности отдельных событий, а в теме
«Случайные величины» вычисляют
вероятности всех событий пространства
исходов опыта.
65. Какое основное условие случайного события позволяет перейти от задач теории вероятностей к задачам математической статистики?
• Его статистическая устойчивость: прибольшом числе испытаний, проведенных в
одних и тех же условиях, частота появления
случайного события одинакова для выборок
разного объема.
66. Как называется закон, подтверждающий это свойство случайного события?
• Закон больших чисел Якоба Бернулли.67. Викторина часть 1
Викторина часть 1математика и поэзия
68. Викторина часть 1 математика и поэзия
Викторина часть 1математика и поэзия
69. Викторина часть 1 математика и поэзия
Викторина часть 1математика и поэзия
70. Математика и поэзия
• Наблюдения показывают, что каждый третий лебедь невозвращается в родные северные края после зимних
странствий: много всяких невзгод и неожиданностей
подстерегает их в пути. Предположим, что
благополучный перелет для каждого лебедя является
независимым от других лебедей случайным событием.
Осенью орнитологи сумели зарегистрировать каждую
особь в большом количестве лебединых стай. Каждая
стая состояла всего из семи лебедей. Какая примерно
доля этих стай вернется весной в любимые места
своих гнездований в полном составе?
71.
Дано:Испытание –
перелет одного лебедя
Событие А –
перелет для лебедя закончился неблагополучно
P(A) =
1/3
n=7–
число испытаний
Событие В –
стая вернется в места гнездований в полном составе
Найти:
P(B), N B
72.
Решение:«Успех» благополучный перелет одного лебедя
p=
= 1 - P(A)
«Неудача» лебедь не вернулся,
q=
= P(A) = 1/3
Событие B –
стая вернулась в полном составе
P(B) =
= P7(7)
Ответ:
6 стай из 100 возвращается в полном составе.
73. Золотая макрель
74. Золотая макрель
Жил старик со своею старухой…Ровно тридцать лет и три года. Старик ловил
неводом рыбу, соблюдал указ рыбнадзора: в день по 7
штук и ни больше, ни меньше.
Что поймает, все за день съедали. Был у них еще кот
долгожитель. Привередливый, пуще старухи. Он
питался одной лишь макрелью. Но макрель
попадалась в сети вдвое реже, чем прочие рыбы. Для
кота же в течение жизни уж 700 дней набралось
голодных.
А теперь посчитайте, сколько дней прожил кот к
данному моменту.
75.
Дано:Испытание –
поймать одну рыбу
n=7–
число испытаний
Событие А –
пойманная рыба не макрель
P(A) =
2/3
Событие В –
день голодный
NВ =
700 – число голодных дней
Найти:
P(B), N
76.
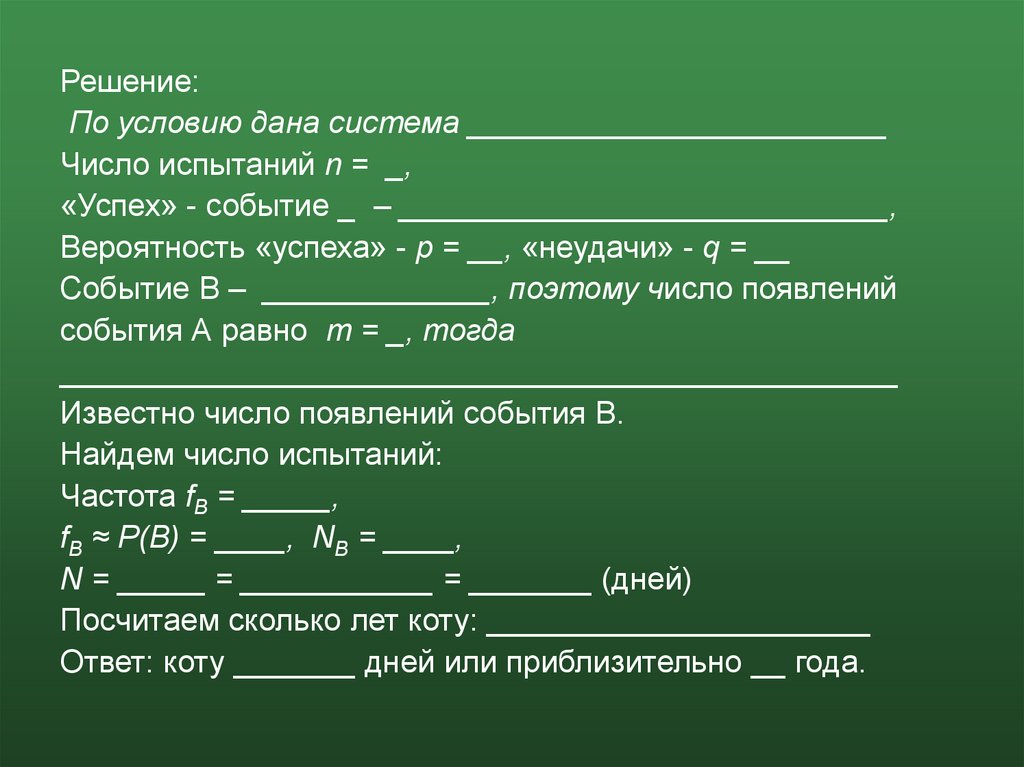
Решение:По условию дана система ________________________
Число испытаний n = _,
«Успех» - событие _ – ____________________________,
Вероятность «успеха» - p = __, «неудачи» - q = __
Событие В – _____________, поэтому число появлений
события А равно m = _, тогда
________________________________________________
Известно число появлений события В.
Найдем число испытаний:
Частота fB = _____,
fB ≈ P(B) = ____, NB = ____,
N = _____ = ___________ = _______ (дней)
Посчитаем сколько лет коту: ______________________
Ответ: коту _______ дней или приблизительно __ года.
77.
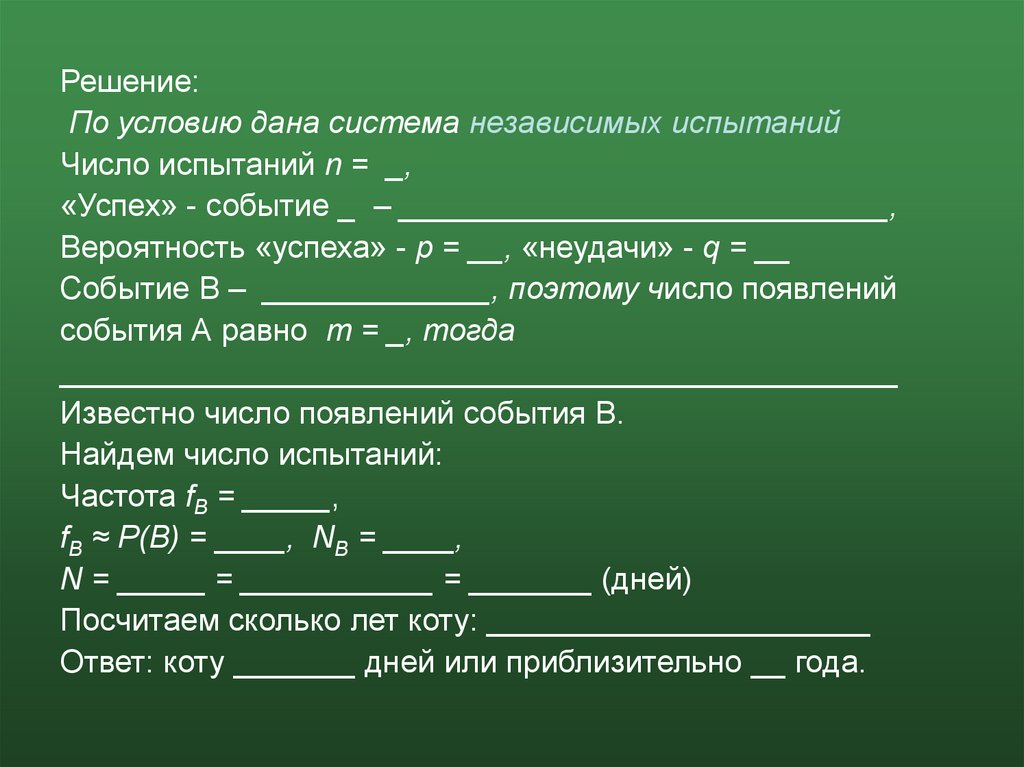
Решение:По условию дана система независимых испытаний
Число испытаний n = _,
«Успех» - событие _ – ____________________________,
Вероятность «успеха» - p = __, «неудачи» - q = __
Событие В – _____________, поэтому число появлений
события А равно m = _, тогда
________________________________________________
Известно число появлений события В.
Найдем число испытаний:
Частота fB = _____,
fB ≈ P(B) = ____, NB = ____,
N = _____ = ___________ = _______ (дней)
Посчитаем сколько лет коту: ______________________
Ответ: коту _______ дней или приблизительно __ года.
78.
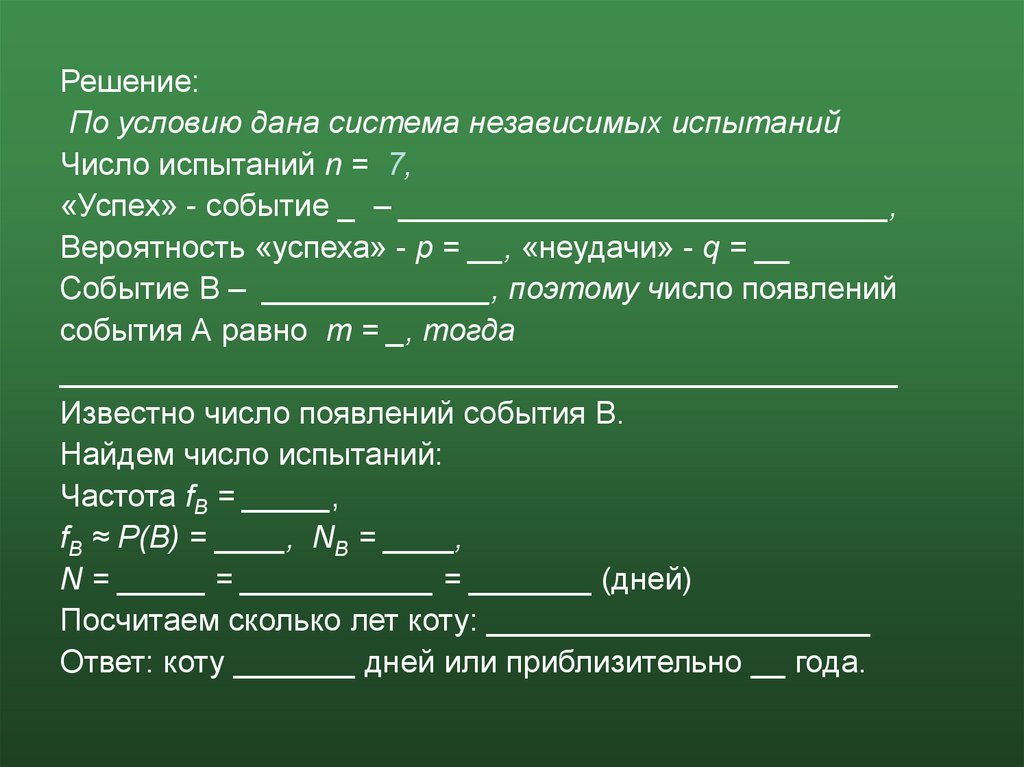
Решение:По условию дана система независимых испытаний
Число испытаний n = 7,
«Успех» - событие _ – ____________________________,
Вероятность «успеха» - p = __, «неудачи» - q = __
Событие В – _____________, поэтому число появлений
события А равно m = _, тогда
________________________________________________
Известно число появлений события В.
Найдем число испытаний:
Частота fB = _____,
fB ≈ P(B) = ____, NB = ____,
N = _____ = ___________ = _______ (дней)
Посчитаем сколько лет коту: ______________________
Ответ: коту _______ дней или приблизительно __ года.
79.
Решение:По условию дана система независимых испытаний
Число испытаний n = 7,
«Успех» - событие А – пойманная рыба не макрель,
Вероятность «успеха» - p = __, «неудачи» - q = __
Событие В – _____________, поэтому число появлений
события А равно m = _, тогда
________________________________________________
Известно число появлений события В.
Найдем число испытаний:
Частота fB = _____,
fB ≈ P(B) = ____, NB = ____,
N = _____ = ___________ = _______ (дней)
Посчитаем сколько лет коту: ______________________
Ответ: коту _______ дней или приблизительно __ года.
80.
Решение:По условию дана система независимых испытаний
Число испытаний n = 7,
«Успех» - событие А – пойманная рыба не макрель,
Вероятность «успеха» - p = 2/3, «неудачи» - q = 1/3
Событие В – _____________, поэтому число появлений
события А равно m = _, тогда
________________________________________________
Известно число появлений события В.
Найдем число испытаний:
Частота fB = _____,
fB ≈ P(B) = ____, NB = ____,
N = _____ = ___________ = _______ (дней)
Посчитаем сколько лет коту: ______________________
Ответ: коту _______ дней или приблизительно __ года.
81.
Решение:По условию дана система независимых испытаний
Число испытаний n = 7,
«Успех» - событие А – пойманная рыба не макрель,
Вероятность «успеха» - p = 2/3, «неудачи» - q = 1/3
Событие В – день голодный, поэтому число появлений
события А равно m = _, тогда
________________________________________________
Известно число появлений события В.
Найдем число испытаний:
Частота fB = _____,
fB ≈ P(B) = ____, NB = ____,
N = _____ = ___________ = _______ (дней)
Посчитаем сколько лет коту: ______________________
Ответ: коту _______ дней или приблизительно __ года.
82.
Решение:По условию дана система независимых испытаний
Число испытаний n = 7,
«Успех» - событие А – пойманная рыба не макрель,
Вероятность «успеха» - p = 2/3, «неудачи» - q = 1/3
Событие В – день голодный, поэтому число появлений
события А равно m = 7, тогда вероятность события В
________________________________________________
Известно число появлений события В.
Найдем число испытаний:
Частота fB = _____,
fB ≈ P(B) = ____, NB = ____,
N = _____ = ___________ = _______ (дней)
Посчитаем сколько лет коту: ______________________
Ответ: коту _______ дней или приблизительно __ года.
83.
Решение:По условию дана система независимых испытаний
Число испытаний n = 7,
«Успех» - событие А – пойманная рыба не макрель,
Вероятность «успеха» - p = 2/3, «неудачи» - q = 1/3
Событие В – день голодный, поэтому число появлений
события А равно m = 7, тогда вероятность события В:
Известно число появлений события В.
Найдем число испытаний:
Частота fB = _____,
fB ≈ P(B) = ____, NB = ____,
N = _____ = ___________ = _______ (дней)
Посчитаем сколько лет коту: ______________________
Ответ: коту _______ дней или приблизительно __ года.
84.
Решение:По условию дана система независимых испытаний
Число испытаний n = 7,
«Успех» - событие А – пойманная рыба не макрель,
Вероятность «успеха» - p = 2/3, «неудачи» - q = 1/3
Событие В – день голодный, поэтому число появлений
события А равно m = 7, тогда
Известно число появлений события В.
Найдем число испытаний:
Частота fB = NB / N,
fB ≈ P(B) = ____, NB = ____,
N = _____ = ___________ = _______ (дней)
Посчитаем сколько лет коту: ______________________
Ответ: коту _______ дней или приблизительно __ года.
85.
Решение:По условию дана система независимых испытаний
Число испытаний n = 7,
«Успех» - событие А – пойманная рыба не макрель,
Вероятность «успеха» - p = 2/3, «неудачи» - q = 1/3
Событие В – день голодный, поэтому число появлений
события А равно m = 7, тогда
Известно число появлений события В.
Найдем число испытаний:
Частота fB = NB / N,
fB ≈ P(B) = 0.0585, NB = 700,
N = _____ = ___________ = _______ (дней)
Посчитаем сколько лет коту: ______________________
Ответ: коту _______ дней или приблизительно __ года.
86.
Решение:По условию дана система независимых испытаний
Число испытаний n = 7,
«Успех» - событие А – пойманная рыба не макрель,
Вероятность «успеха» - p = 2/3, «неудачи» - q = 1/3
Событие В – день голодный, поэтому число появлений
события А равно m = 7, тогда
Известно число появлений события В.
Найдем число испытаний:
Частота fB = NB / N,
fB ≈ P(B) = 0.0585, NB = 700,
N = NB / fB = 700 / 0.0585 = 11 966 (дней)
Посчитаем сколько лет коту: ______________________
Ответ: коту _______ дней или приблизительно __ года.
87.
Решение:По условию дана система независимых испытаний
Число испытаний n = 7,
«Успех» - событие А – пойманная рыба не макрель,
Вероятность «успеха» - p = 2/3, «неудачи» - q = 1/3
Событие В – день голодный, поэтому число появлений
события А равно m = 7, тогда
Известно число появлений события В.
Найдем число испытаний:
Частота fB = NB / N,
fB ≈ P(B) = 0.0585, NB = 700,
N = NB / fB = 700 / 0.0585 = 11 966 (дней)
Посчитаем сколько лет коту: 11 966 / 365 ≈ 33 года
Ответ: коту _______ дней или приблизительно __ года.
88.
Решение:По условию дана система независимых испытаний
Число испытаний n = 7,
«Успех» - событие А – пойманная рыба не макрель,
Вероятность «успеха» - p = 2/3, «неудачи» - q = 1/3
Событие В – день голодный, поэтому число появлений
события А равно m = 7, тогда
Известно число появлений события В.
Найдем число испытаний:
Частота fB = NB / N,
fB ≈ P(B) = 0.0585, NB = 700,
N = NB / fB = 700 / 0.0585 = 11 966 (дней)
Посчитаем сколько лет коту: 11 966 / 365 ≈ 33 года
Ответ: коту 11 966 дней или приблизительно 33 года.
89. Викторина часть 2
Викторина часть 290. ВИКТОРИНА
1. Суммой двух случайных событий называют появление обоихэтих случайных событий в одном испытании?
1. Необходимое условие случайного события – его редкость?
2. Закон редких событий – это закон Пуассона?
2. Произведением двух случайных событий называют появление
обоих этих случайных событий в одном испытании?
3. Несовместные случайные события всегда противоположны?
3. Если вероятность события равна единице, то это событие
достоверное?
91.
4. Формула Бернулли позволяет узнать, сколько разпроизойдет событие А при N испытаниях?
4. Выборка – это подмножество генеральной
совокупности?
5. Дисперсия числа π равна нулю?
5. Биномиальный закон – это закон Пуассона?
6. Вероятность достоверного события не меньше единицы?
6. Дисперсия всегда положительна?
7. Частота безразмерна?
7. Противоположные случайные события всегда
несовместны?
92.
8. Математическое ожидание всегда положительно?8. Математическое ожидание числа π равно нулю?
9. В формуле
n – это число испытаний?
9. Функция распределения полностью описывает все
свойства любой случайной величины?
10. Закон редких событий Пуассона является предельным
случаем закона распределения Я. Бернулли?
10. Если при 500 опытах событие А произошло 11 раз, то
можно утверждать, что А есть случайное событие?
93.
11. Дисперсия случайной величины может бытьотрицательной?
11. Математическое ожидание – это среднее значение
случайной величины?
12. Математическое ожидание случайной величины – это
величина неслучайная?
12. Формулу Бернулли можно применять при большом
числе испытаний?
13. Вероятность события – величина постоянная?
13. Частота появления события меняется от опыта к
опыту?
94.
14. Если при трех подбрасываниях монеты герб выпалдважды, то можно утверждать, что частота появления
события А – при подбрасывании монеты выпал герб равна
2/3?
14. Функция Лапласа F(x) – четная?
15. В схеме независимых испытаний для редких событий
можно применять формулу Лапласа?
15. В биномиальном законе распределения M(X) = D(X)?
95. ВИКТОРИНА
1. Суммой двух случайных событий называют появление обоихэтих случайных событий в одном испытании? Нет
1. Необходимое условие случайного события – его редкость?
Нет
2. Закон редких событий – это закон Пуассона? Да
2. Произведением двух случайных событий называют появление
обоих этих случайных событий в одном испытании? Да
3. Несовместные случайные события всегда противоположны? Нет
3. Если вероятность события равна единице, то это событие
достоверное? Нет
96.
4. Формула Бернулли позволяет узнать, сколько раз произойдетсобытие А при N испытаниях? Нет
4. Выборка – это подмножество генеральной совокупности? Да
5. Дисперсия числа π равна нулю? Да
5. Биномиальный закон – это закон Пуассона? Нет
6. Вероятность достоверного события не меньше единицы? Да
6. Дисперсия всегда положительна? Да
7. Частота безразмерна? Да
7. Противоположные случайные события всегда несовместны?
Да
97.
8. Математическое ожидание всегда положительно? Нет8. Математическое ожидание числа π равно нулю? Нет
9. В формуле
n – это число испытаний?
Нет
9. Функция распределения полностью описывает все
свойства любой случайной величины? Да
10. Закон редких событий Пуассона является предельным
случаем закона распределения Я. Бернулли? Да
10. Если при 500 опытах событие А произошло 11 раз, то
можно утверждать, что А есть случайное событие?
Нет
98.
11. Дисперсия случайной величины может бытьотрицательной? Нет
11. Математическое ожидание – это среднее значение
случайной величины? Да
12. Математическое ожидание случайной величины – это
величина неслучайная? Да
12. Формулу Бернулли можно применять при большом
числе испытаний? Да
13. Вероятность события – величина постоянная? Да
13. Частота появления события меняется от опыта к
опыту? Да
99.
14. Если при трех подбрасываниях монеты герб выпалдважды, то можно утверждать, что частота появления
события А – при подбрасывании монеты выпал герб равна
2/3? Нет
14. Функция Лапласа F(x) – четная? Нет
15. В схеме независимых испытаний для редких событий
можно применять формулу Лапласа? Да
15. В биномиальном законе распределения M(X) = D(X)?
Нет
100. оценка за викторину:
• «3» - от 8-ми до 10-ти правильных ответов,• «4» - от 11-ти до 13-ти,
• «5» - 14 или 15 правильных ответов.

































































































 Математика
Математика








