Структурный анализ и синтез механизмов

1. Структурный анализ и синтез механизмов

Лекция по дисциплине «Теория механизмов
и машин (ТММ)»
2 часа
Старший преподаватель
Стрыгин Сергей Васильевич

2. Вопросы

1. Основной принцип
образования рычажных механизмов.
2. Группы Ассура.
3. Виды механизмов
и их структурные схемы.
2

3. ВВЕДЕНИЕ

Анализ фундаментальных исследований в области теории
структуры механических систем, начатых во второй половине
XIX века трудами П.Л. Чебышева, Ф. Рело, М. Грюблера, Х.И.
Гохмана, О.П. Сомова, показывает, что их результат позволил
выделить теорию машин в самостоятельную науку со своими
предметом и методами исследования.
В течение XX века благодаря исследованиям Л.В. Ассура,
А.П. Малышева, В.В. Добровольского, Н.И. Колчина, И.И.
Артоболевского, С.Н. Кожевникова, О.Г. Озола, Л.Н. Решетова и
других ученых теория структуры механизмов была развита до
ее прямого использования в практике машиностроения.
Анализ трудов перечисленных исследователей показал,
что к началу XXI века были выявлены принципы построения
кинематических цепей, определены основы их классификации и
разработаны методы их исследования.
3

4. Основной принцип образования рычажных механизмов

Леони́д Влади́мирович Ассу́р
(31 марта 1878, Рыбинск — 19 мая 1920,
Воронеж) — русский и советский
механик и машиновед, труды которого
по кинематике и динамике механизмов
заложили
теоретические
основы
советской школы по теории механизмов
и машин.
В частности Л. В. Ассур открыл общую
закономерность в структуре многозвенных плоских
механизмов, применяемую и сейчас при их анализе и
синтезе. Он же разработал метод «особых точек» для
кинематического
анализа
сложных
рычажных4
механизмов.

5. Основной принцип образования рычажных механизмов (продолжение)

Для раскрытия содержания темы
терминологией теории механизмов и машин.
требуется
владение
Рычажный механизм - механизм, звенья которого образуют
только низшие пары.
Кинематическая пара - соединение двух твердых
механизма, допускающее их заданное относительное движение.
тел
По виду соединения звеньев кинематические пары разделяют на
низшие и высшие.
Низшей кинематической парой называется соединение звеньев
по поверхности. Такая поверхность может быть цилиндрической,
плоской, сферической или криволинейной.
5

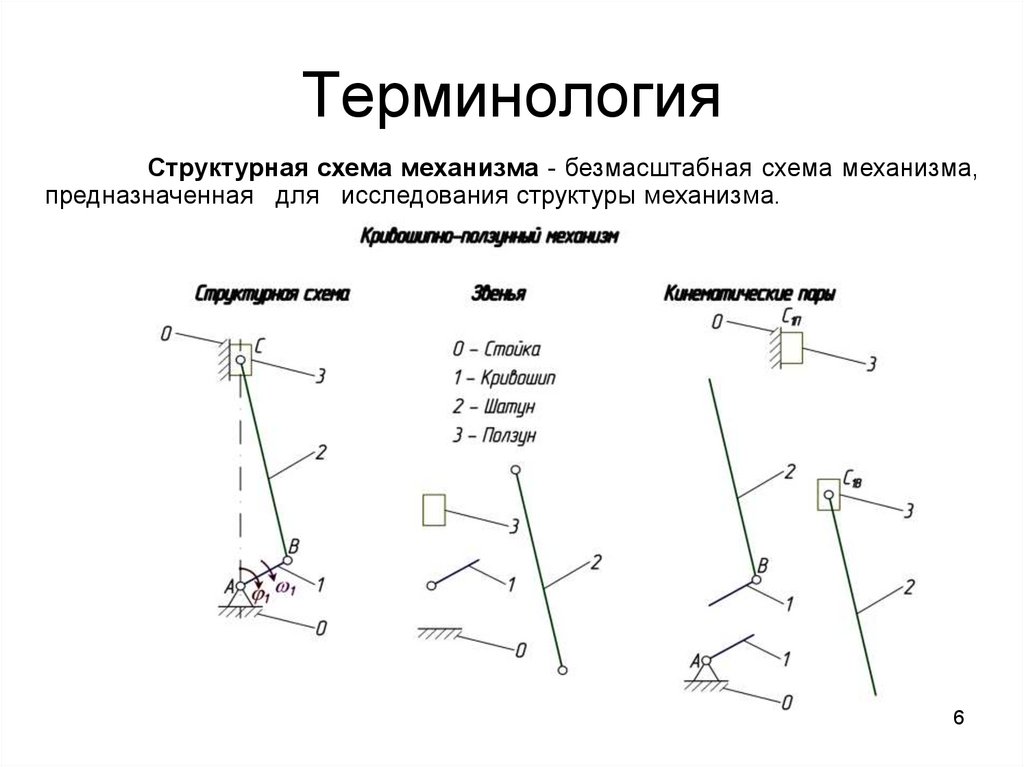
6. Терминология

Структурная схема механизма - безмасштабная схема механизма,
предназначенная для исследования структуры механизма.
6

7. Терминология (продолжение)

Высшей кинематической парой называется соединение
звеньев по линиям или в точках. Примерами таких пар являются
соединение шара с плоскостью, ролика с криволинейной
поверхностью, двух зубьев, находящихся в зацеплении
зубчатых колес.
Кинематические пары также разделяют по числу степеней
свободы в относительном движении соединяемых ими звеньев
и числу связей.
Числом степеней свободы звеньев кинематической
пары, называется число независимых возможных движений
одного звена относительно другого.
Связями или условиями связи кинематической пары
называются ограничения, накладываемые на относительные
движения звеньев.
Класс кинематической пары определяется числом
условий связи равным от 1 до 5.
7

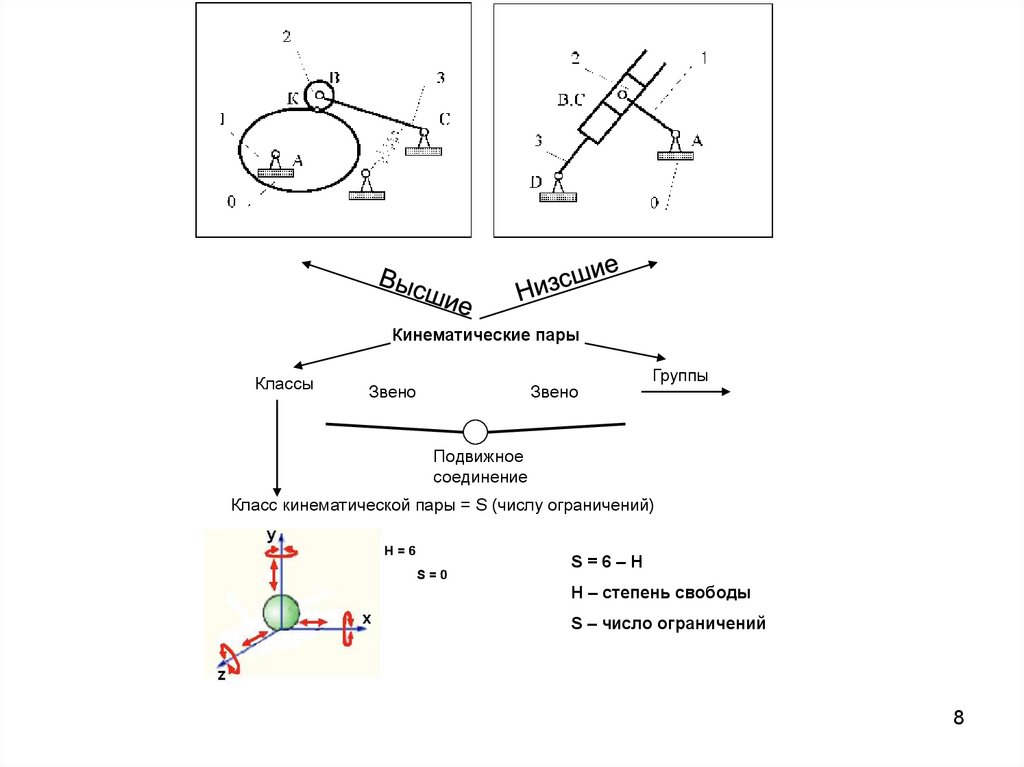
8.

Кинематические пары
Классы
Звено
Звено
Группы
Подвижное
соединение
Класс кинематической пары = S (числу ограничений)
H=6
S=0
S=6–H
H – степень свободы
S – число ограничений
8

9. Терминология (продолжение)

Структурным синтезом называется проектирование структурной
схемы механизма, на основании определения ее неизвестных
параметров по заданным.
Одной из задач структурного синтеза является проектирование
структурной схемы механизма по заданному числу степеней свободы.
При решении этой задачи могут применяться аналитический метод
синтеза, основанный на использовании формул А.П. Малышева и П.Л.
Чебышева
для
определения
числа
степеней
свободы
пространственного и плоского механизмов, и метод присоединения
особых кинематических цепей, называемых структурными группами
или группами Ассура.
9

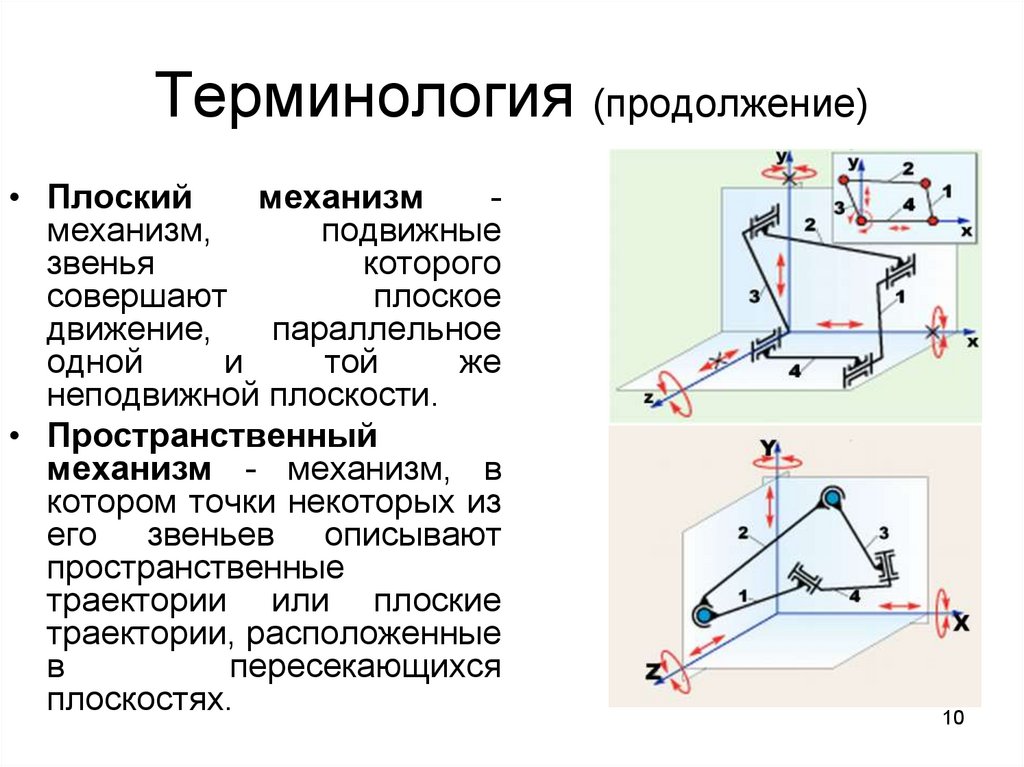
10. Терминология (продолжение)

• Плоский
механизм
механизм,
подвижные
звенья
которого
совершают
плоское
движение,
параллельное
одной
и
той
же
неподвижной плоскости.
• Пространственный
механизм - механизм, в
котором точки некоторых из
его звеньев описывают
пространственные
траектории или плоские
траектории, расположенные
в
пересекающихся
плоскостях.
10

11. Терминология (окончание)

• Кинематическая цепь - система
звеньев
и/или
твердотельных
элементов
механизма,
образующих
между
собой
кинематические пары.
• Элемент механизма - твердотельный,
жидкостной или газовый
компонент
механизма,
обеспечивающий
взаимодействие
его
звеньев,
не
контактирующих непосредственно друг с
другом.
• Стойка - звено, принимаемое условно за
неподвижное.
11

12. Основной принцип образования рычажных механизмов (продолжение)

Существуют общие закономерности в структуре (строении)
самых различных механизмов, связывающие число степеней
свободы W механизма с числом звеньев и числом и видом его
кинематических пар. Эти закономерности носят название
структурных формул механизмов.
А. П. Малышев (1879 — 1962) предложил теорию
структурного анализа и синтеза применительно к сложным
плоским и пространственным механизмам.
Для пространственных механизмов в настоящее время
наиболее распространена формула А.П. Малышева, вывод
которой производится следующим образом.
12

13. Основной принцип образования рычажных механизмов (продолжение)

Пусть в механизме, имеющем m звеньев (включая стойку), p1, p2,
p3, p4, p5 – число одно-, двух-, трех-, четырех- и пятиподвижных пар.
Число подвижных звеньев обозначим n = m - 1. Если бы все подвижные
звенья были свободными телами, общее число степеней свободы было
бы равно 6n.
Однако одноподвижная пара V
класса накладывает на
относительное движение звеньев, образующих пару, 5 связей, каждая
двухподвижная пара IV класса – 4 связи и т. д. Следовательно, общее
число степеней свободы, равное шести, будет уменьшено на величину
5
( 6 - i )pi 5p1 4p2 3p3 2p4 p5
i 1
где i = H – подвижность кинематической пары, pi – число пар,
подвижность которых равна i.
13

14. Основной принцип образования рычажных механизмов (продолжение)

В общее число наложенных связей может войти некоторое число
q избыточных (повторных) связей, которые дублируют другие связи, не
уменьшая подвижности механизмов, а только обращая его в
статически неопределенную систему.
Поэтому число степеней
свободы пространственного механизма, равное числу степеней
свободы его подвижной кинематической цепи относительно стойки,
определяется по следующей формуле Малышева:
W = 6n – (5p1 + 4p2 + 3p3 + 2p4 + p5 – q),
или в краткой записи
5
W 6n – [ ( 6 - i )pi – q];
i 1
при q = 0 механизм – статически определенная система,
при q > 0 – статически неопределенная система.
14

15.

Основной принцип
образования рычажных механизмов
(продолжение)
Для плоских механизмов без
избыточных
связей
структурная
формула носит имя П. Л. Чебышева,
впервые предложившего ее в 1869
году для рычажных механизмов с
вращательными парами и одной
степенью свободы. В настоящее
время
формула
Чебышева
распространяется на любые простые
механизмы и выводится с учетом
избыточных
связей
следующим
образом.
Пусть в плоском механизме, имеющем m звеньев (включая стойку), n =
= m-1 – число подвижных звеньев, Pн – число низших пар и Pв – число высших
пар. Если бы все подвижные звенья были свободными телами, совершающими
плоское движение, общее число степеней свободы было бы равно 3n. Однако
каждая низшая пара накладывает на относительное движение звеньев,
образующих пару, две связи, оставляя одну степень свободы, а каждая высшая
пара накладывает одну связь, оставляя две степени свободы.
15

16.

Основной принцип
образования рычажных механизмов
(продолжение)
В число наложенных связей может
войти некоторое число qП избыточных
повторных связей, устранение которых
не
увеличивает
подвижности
механизма.
Следовательно,
число
степеней свободы плоского механизма,
т. е. число степеней свободы его
подвижной
кинематической
цепи
относительно стойки, определяется по
следующей формуле Чебышева:
WП = 3n – (2pН + pВ – qП).
связей
Если известно WП, отсюда можно найти число избыточных
qП = WП - 3n + 2pН + pВ .
16

17.

Основной принцип
образования рычажных механизмов
(окончание)
Метод структурного синтеза путем присоединения структурных групп
(метод Ассура) заключается в присоединении этих групп к одному или
нескольким начальным звеньям и стойке или к ранее присоединенным
структурным группам. Особенность структурных групп заключается в том,
что число их степеней свободы относительно тех звеньев исходного
механизма, к которым они присоединяются, равно нулю, и присоединение
структурной группы не изменяет числа степеней свободы исходного
механизма. Присоединение структурной группы позволяет получить новый
механизм с тем же числом степеней свободы, что и у исходного. Другая
особенность структурных групп заключается в том, что они не
распадаются на более простые кинематические цепи, удовлетворяющие
этому условию. Исходя из этого, можно дать следующее определение
понятию «структурная группа».
17

18.

Группы Ассура
Структурной
группой
(группой
Ассура)
называется
кинематическая цепь, присоединение которой к исходному механизму
не изменяет числа его степеней свободы и которая не может
распадаться на более простые кинематические цепи, обладающие
таким же свойством.
На следующем слайде показан пример структурного синтеза
плоского шестизвенного шарнирного механизма методом Ассура. При
синтезе исходной структурной группой I является двухзвенный
механизм, состоящий из стойки 0 и подвижного звена 1 с числом
степеней свободы W = 1. При синтезе к исходному механизму
присоединяются структурные группы II и III с числом степеней свободы
W = 0, в результе чего образуется механизм с заданными свойствами,
одним из которых является число степеней свободы механизма W = 1.
18

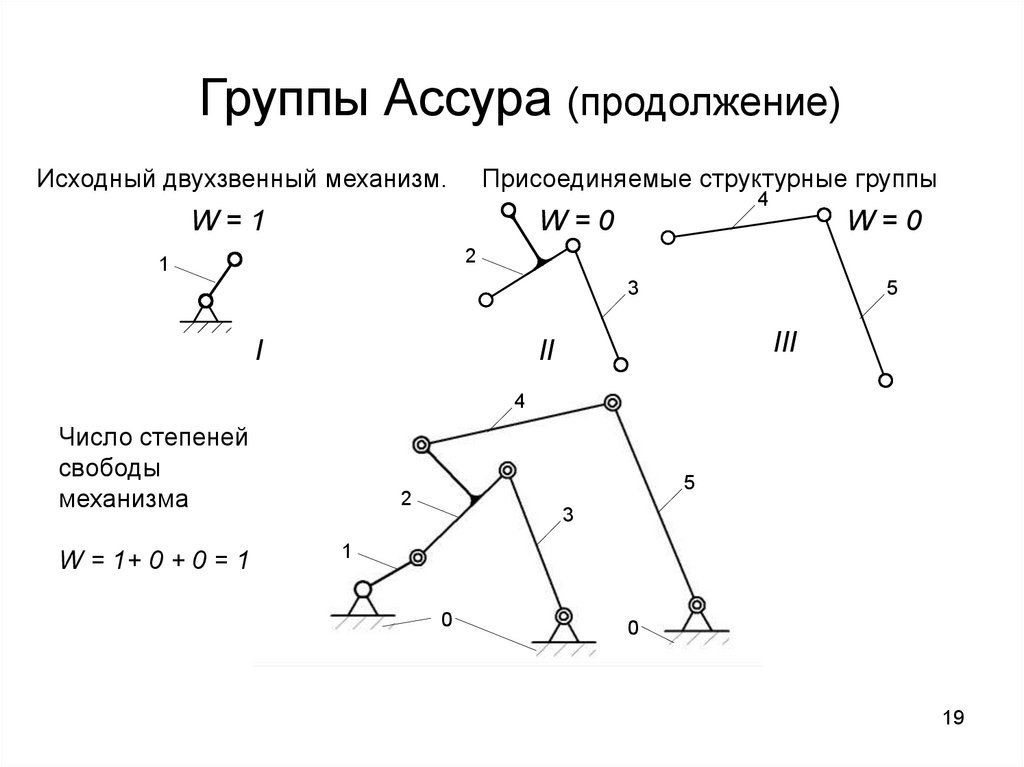
19.

Группы Ассура (продолжение)
Исходный двухзвенный механизм.
Присоединяемые структурные группы
W=1
4
W=0
W=0
2
1
3
I
5
III
II
4
Число степеней
свободы
механизма
W = 1+ 0 + 0 = 1
5
2
3
1
0
0
19

20.

Группы Ассура (продолжение)
• Кинематические цепи делятся на классы. К первому классу
относится двухзвенный механизм с числом степеней свободы W =
= 1, состоящий из одного подвижного звена и стойки. С подвижным
звеном 1 связана обобщенная координата φ1. К этому механизму
последовательно присоединяют структурные группы, состоящие из
звеньев 2-3 и 4-5 с W = 0 и получают шестизвенный механизм с
одной степенью свободы. Из условия W = 0 число звеньев и
кинематических пар в структурных группах подчиняется
соотношению 3n - 2p1 = 0.
• Ко второму классу условно относят двухповодковую
(двухзвенную) группу, к третьему и более высоким классам
относятся структурные группы, в состав которых входят
кинематические пары, образующие замкнутый контур.
20

21.

Группы Ассура (окончание)
Кроме деления на классы, структурные группы разделяются на порядки.
Порядком структурной группы называется число свободных элементов
кинематических
пар,
присоединяемых
к
исходному
механизму.
Трехповодковая структурная группа является группой третьего порядка, так
как содержит три свободных элемента кинематических пар, образуемых
звеньями при их присоединении к исходному механизму.
Замкнутый контур в структурной группе может быть представлен
внутренним звеном в виде отрезка прямой линии, соединенным со
свободными звеньями.
Механизмы, как и структурные группы, также делятся на классы. Класс
механизма определяется наивысшим классом входящей в него структурной
группы.
Таким образом, с помощью структурного синтеза по методу Ассура
выбирают структурную схему механизма, удовлетворяющую поставленной
21
задаче синтеза.

22. Виды механизмов и их структурные схемы

Существенный вклад в становление
механики машин как цельной теории
машиностроения внес Иван Иванович
Артоболевский (1905 — 1977).
Он является организатором отечественной
школы теории механизмов и машин; им написаны
многочисленные труды по структуре, кинематике и
синтезу механизмов, динамике машин и теории
машин-автоматов, а также учебники, получившие
всеобщее признание.
22

23. Артоболевский И.И. Механизмы в современной технике. В 7 томах

И.И.
Артоболевский
–
автор
многотомного
справочного
пособия
«Механизмы в современной
технике». [Справочное пособие.
2-е издание, переработанное.
(Москва:
Издательство
«Наука».
Главная редакция
физико-математической
литературы, 1979)].
Том 1. Элементы механизмов.
Простейшие рычажные и
шарнирно-рычажные
механизмы.
Том 2. Кулисно-рычажные и
кривошипно-ползунные
механизмы.
Том 3. Рычажно-кулачковые,
рычажно-зубчатые, рычажнохраповые, рычажноклиновые и винто-рычажные
механизмы. Механизмы с
гибкими и упругими
звеньями.
Том 4. Зубчатые механизмы.
Том 5. Кулачковые и
фрикционные механизмы.
Механизмы с гибкими
звеньями.
Том 6. Электрические
механизмы.
Том 7. Гидравлические и
пневматические механизмы.
23

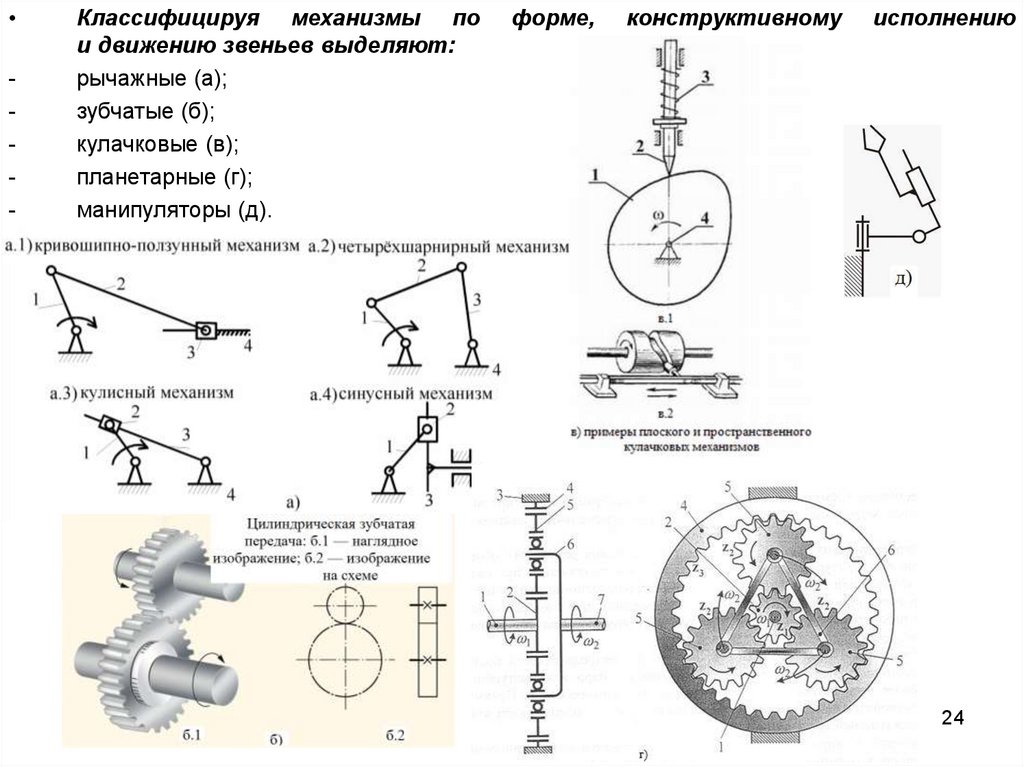
24.

-
Классифицируя механизмы по
и движению звеньев выделяют:
рычажные (а);
зубчатые (б);
кулачковые (в);
планетарные (г);
манипуляторы (д).
форме,
конструктивному
исполнению
24

25.

СПАСИБО ЗА ВНИМАНИЕ!
25