Похожие презентации:
Структурный анализ рычажных механизмов
1. ТММ
ОСНОВНАЯ ЛИТЕРАТУРА:1. Артоболевский, И.И. Теория механизмов и машин : учеб. пособие для
вузов / Гос. комитет по народному образованию. М. : Наука, 1988. – 640 с.,
ил.
2. Кожевников, С.Н. Теория механизмов и машин: учеб. пособие для вузов /
М.: Машиностроение, 1969. – 584 с., ил.
3. Зиновьев, В.А. Курс теории механизмов и машин. Главная редакция
физ.-мат. литературы. М. : Наука, 1972. – 384 с., ил.
4. Попов, С.А., Тимофеев, Г.А. Курсовое проектирование по теории
механизмов и механике машин / под ред. К. В. Фролова; М. : Высшая
школа, 1998. – 351 с., ил.
5. М.Б. Бородина, Б.А. Шевченко, Структурный и кинематический анализ
механизмов. Часть 1. Методические указания по ТММ для студентов всех
форм обучения специальностей ТМ, ММО и А. Старый Оскол, 2005, с. 60.
6. Б.А. Шевченко, М.Б. Бородина, Силовой анализ механизмов. Часть 2.
Методические указания по ТММ для студентов всех форм обучения
специальностей ТМ, ММО и А. Старый Оскол, 2008.
2.
Теория механизмов и машин является одной из первых общеинженерныхдисциплин, которая базируется на фундаментальных дисциплинах: физика,
высшая математика, теоретическая механика.
На материале курса ТММ базируются такие важные для общего инженерного
образования дисциплины, как сопротивление материалов, динамика и
прочность машин, детали машин и многие другие специальные дисциплины.
Для успешного освоения курса стандартом предусмотрено, наряду с изучением
теоретических основ и проведением лабораторного практикума, обязательное
выполнение курсового проекта.
Курсовой проект по этой дисциплине является, по сути дела, первой
комплексной научно-исследовательской работой будущего инженера-механика
на одном из важнейших этапов создания машины – переход от идеи машины,
её принципиальной кинематической схемы и основных технологических
параметров к реальной кинематической схеме с линейными, кинематическими
и силовыми параметрами всех её частей.
3.
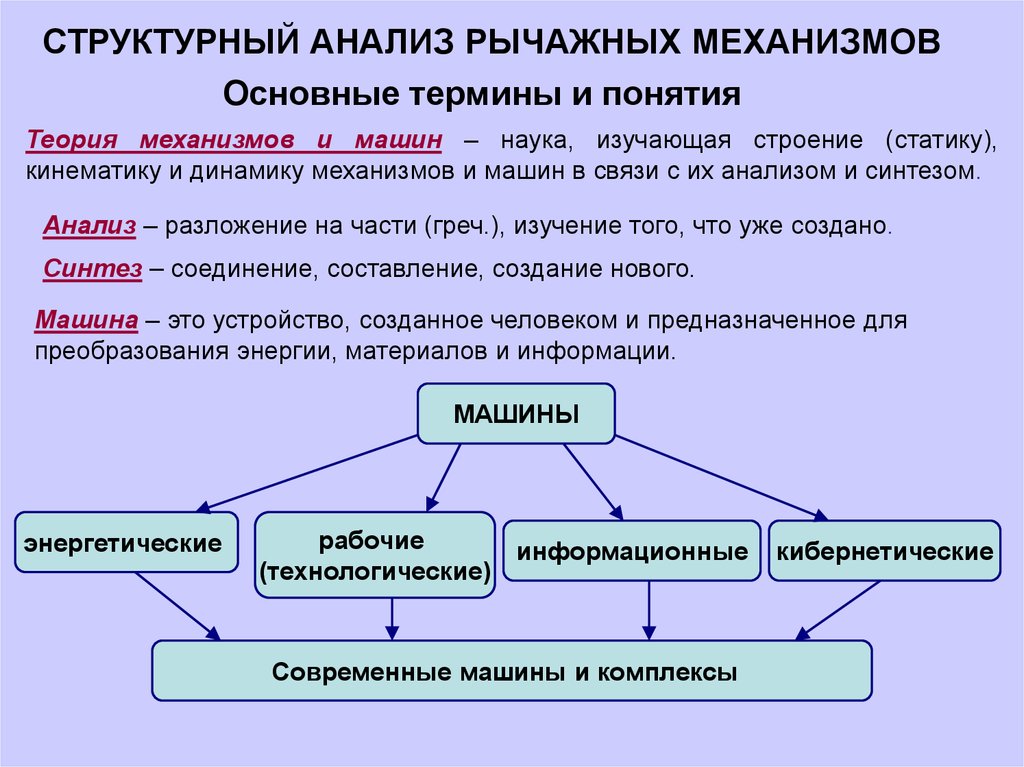
СТРУКТУРНЫЙ АНАЛИЗ РЫЧАЖНЫХ МЕХАНИЗМОВОсновные термины и понятия
Теория механизмов и машин – наука, изучающая строение (статику),
кинематику и динамику механизмов и машин в связи с их анализом и синтезом.
Анализ – разложение на части (греч.), изучение того, что уже создано.
Синтез – соединение, составление, создание нового.
Машина – это устройство, созданное человеком и предназначенное для
преобразования энергии, материалов и информации.
МАШИНЫ
энергетические
рабочие
информационные
(технологические)
Современные машины и комплексы
кибернетические
4.
Механизм (1) – система тел, предназначенная для полезного для человекапреобразования движения.
Существует много классификаций механизмов
(см. Артоболевский, стр. 11-18; Кожевников, стр. 3-34).
По области применения и
функциональному назначению:
- механизмы летательных аппаратов;
- механизмы станков;
- механизмы кузнечных машин и прессов;
- двигателей внутреннего сгорания;
- механизмы промышленных роботов
(манипуляторы);
- механизмы компрессоров;
- механизмы насосов и т.д.
По структурно-конструктивным признакам:
- рычажные (стержневые);
- зубчатые,
- клиновые и винтовые,
- кулачковые,
- фрикционные,
- механизмы с гибкими связями,
- механизмы с остановками;
- механизмы переменной структуры;
- гидравлические и пневматические;
- комбинированные механизмы, и прочие
По числу подвижностей механизма:
- с одной подвижностью W = 1;
- с несколькими подвижностями W > 1:
- суммирующие (интегральные);
- разделяющие (дифференциальные).
По движению и расположению звеньев в
пространстве:
- пространственные;
- плоские;
- сферические.
5.
Механизм собирают из отдельных частей – деталей.Деталь – изделие, изготовленное из однородного по наименованию и марке
материала без применения сборочных операций (ГОСТ 2.101-68).
Звено – одна деталь или группа деталей, неподвижно связанных между собой.
Звенья бывают:
жесткие,
упругие (рессоры,амортизаторы и пр),
гибкие (канаты, ремни, цепи, шланги гидосистемы и пр.).
Звенья стержневых механизмов:
Стойка – неподвижное или принимаемое за неподвижное (корпус автомобиля)
звено механизма.
Кривошип – звено, совершающее полный оборот относительно
стойки.
Коромысло – звено, совершающее неполный
оборот относительно стойки.
Ползун – звено, совершающее поступательное движение
относительно стойки.
Шатун – звено, совершающее плоскопараллельное движение.
6.
Кулисная группа – группа звеньев, где кулиса 1 совершаеткачательные движения относительно стойки, а кулисный камень 2
– сложное движение (переносное – вращательное, а
относительное – поступательное).
Механизм (2) – совокупность неподвижного и подвижных звеньев.
Кинематические пары и их классификация
Кинематическая пара (КП) – соединение
допускающее относительное движение.
двух
звеньев
Места контакта каждого из двух звеньев называют
кинематической пары.
Элементы: низших пар — поверхности,
высших — линии или точки.
механизма,
элементами
Условная
связь
–
ограничения
(геометрические,
кинематические,
динамические), накладываемые на движение (абсолютное или относительное)
свободного твердого тела.
Всякое свободное тело имеет в
пространстве 6 степеней свободы, а на
плоскости – 3.
7.
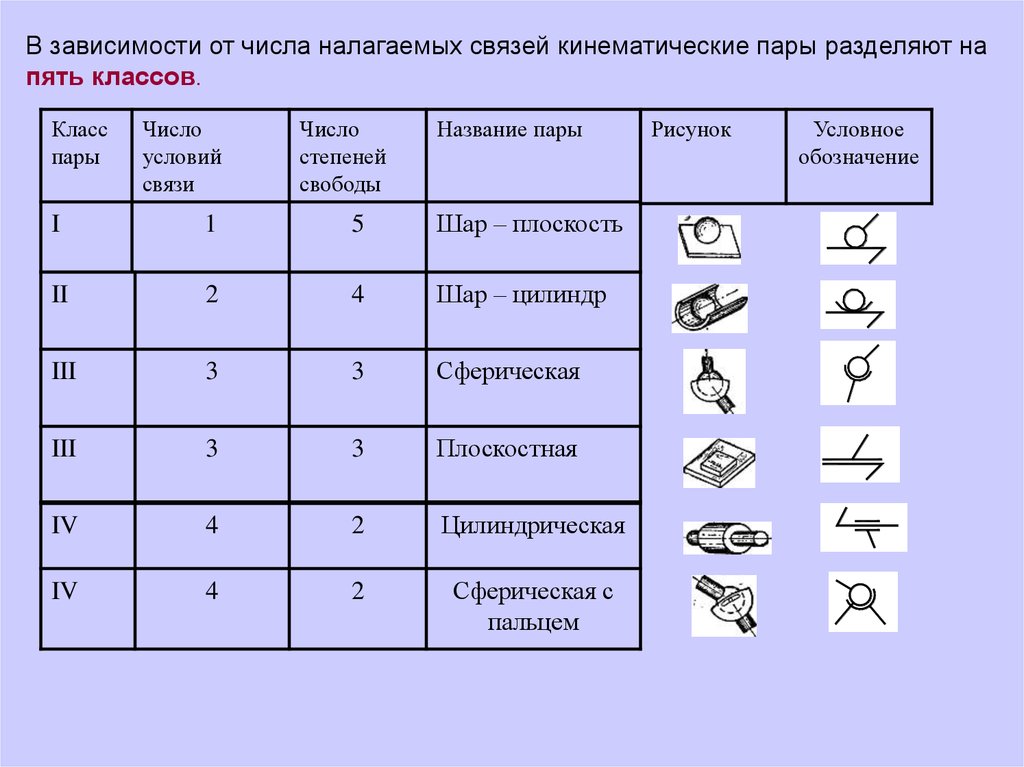
В зависимости от числа налагаемых связей кинематические пары разделяют напять классов.
Класс
пары
Число
условий
связи
Число
степеней
свободы
Название пары
I
1
5
Шар – плоскость
II
2
4
Шар – цилиндр
III
3
3
Сферическая
III
3
3
Плоскостная
IV
4
2
Цилиндрическая
IV
4
2
Сферическая с
пальцем
Рисунок
Условное
обозначение
8.
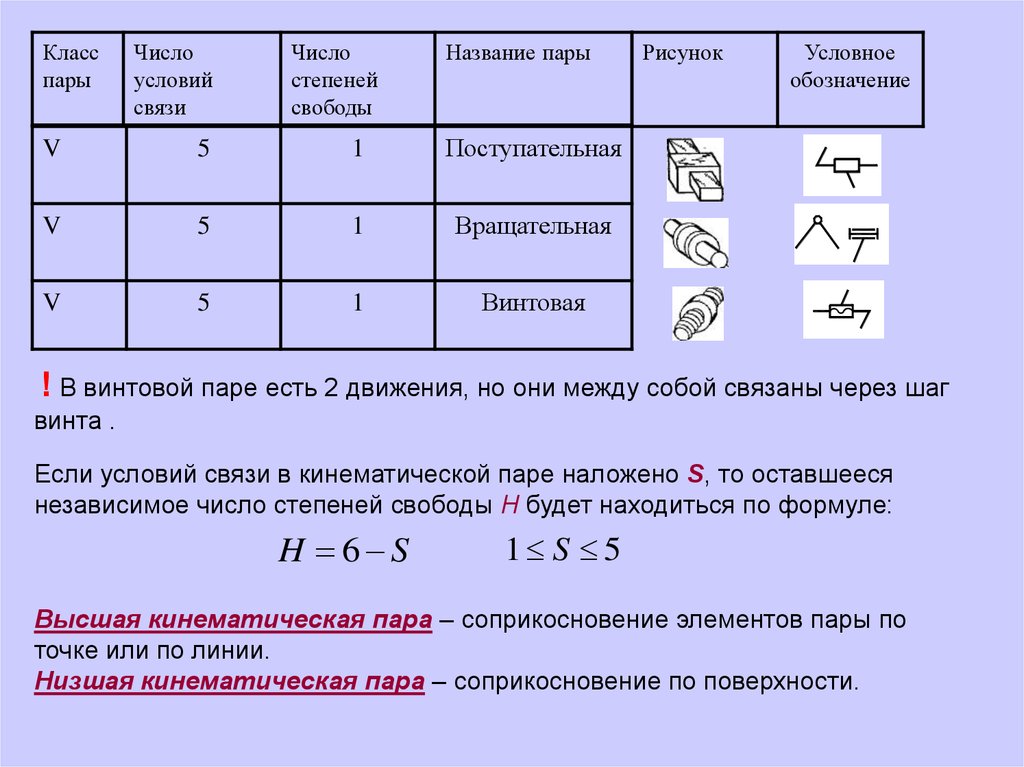
Класспары
Число
условий
связи
Число
степеней
свободы
Название пары
V
5
1
Поступательная
V
5
1
Вращательная
V
5
1
Винтовая
Рисунок
Условное
обозначение
! В винтовой паре есть 2 движения, но они между собой связаны через шаг
винта .
Если условий связи в кинематической паре наложено S, то оставшееся
независимое число степеней свободы H будет находиться по формуле:
H 6 S
1 S 5
Высшая кинематическая пара – соприкосновение элементов пары по
точке или по линии.
Низшая кинематическая пара – соприкосновение по поверхности.
9.
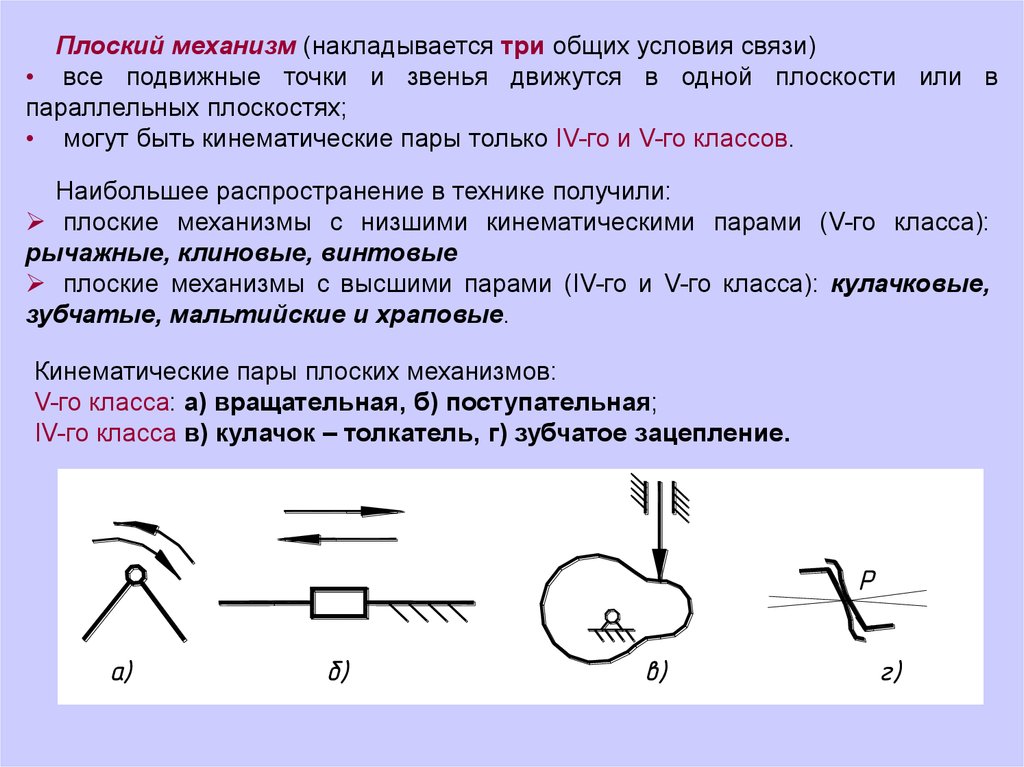
Плоский механизм (накладывается три общих условия связи)• все подвижные точки и звенья движутся в одной плоскости или в
параллельных плоскостях;
• могут быть кинематические пары только IV-го и V-го классов.
Наибольшее распространение в технике получили:
плоские механизмы с низшими кинематическими парами (V-го класса):
рычажные, клиновые, винтовые
плоские механизмы с высшими парами (IV-го и V-го класса): кулачковые,
зубчатые, мальтийские и храповые.
Кинематические пары плоских механизмов:
V-го класса: а) вращательная, б) поступательная;
IV-го класса в) кулачок – толкатель, г) зубчатое зацепление.
10.
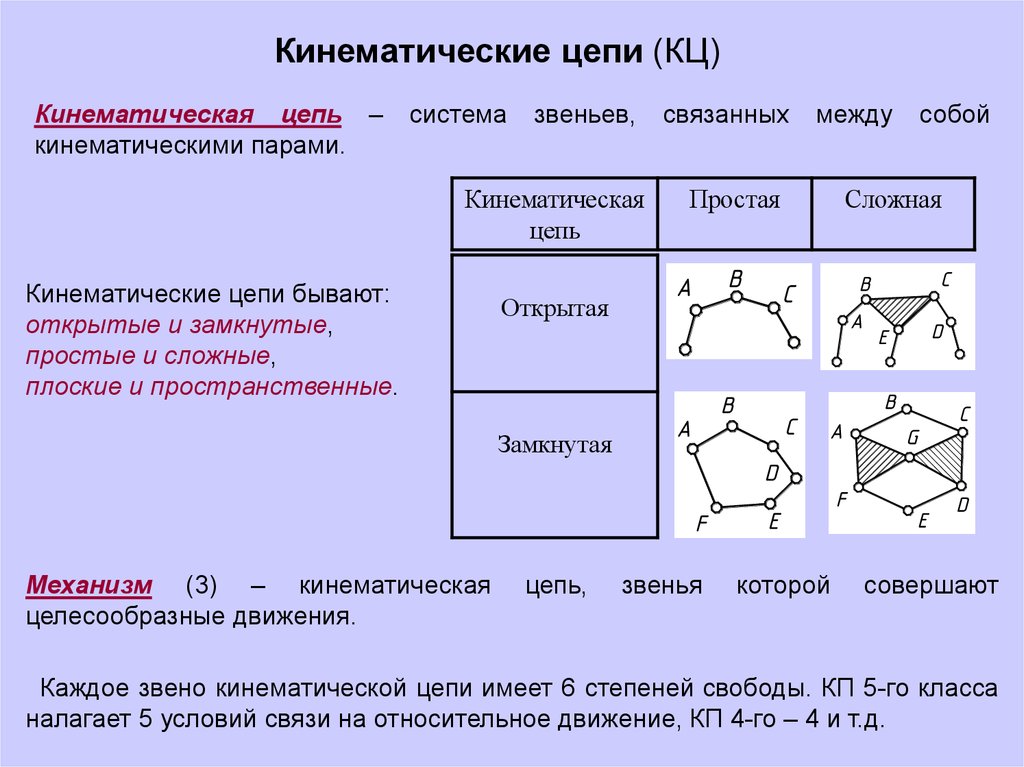
Кинематические цепи (КЦ)Кинематическая цепь –
кинематическими парами.
система
звеньев,
Кинематическая
цепь
Кинематические цепи бывают:
открытые и замкнутые,
простые и сложные,
плоские и пространственные.
связанных
между
Простая
собой
Сложная
Открытая
Замкнутая
Механизм (3) – кинематическая
целесообразные движения.
цепь,
звенья
которой
совершают
Каждое звено кинематической цепи имеет 6 степеней свободы. КП 5-го класса
налагает 5 условий связи на относительное движение, КП 4-го – 4 и т.д.
11.
Если в КЦ всего n звеньев, p5 пар 5-го класса, p4 - 4-го, p3 - 3-го и т.д., точисло степеней свободы H КЦ будет:
H 6 n 5 p5 4 p4 3 p3 2 p2 p1
Подвижность КЦ относительно неподвижного звена называется степенью
подвижности и находится по формуле:
W 6 (n 1) 5 p5 4 p4 3 p3 2 p2 p1
это структурная формула КЦ общего вида (Сомова (1887)– Малышева (1923)).
Согласно принципу образования механизмов, сформулированному впервые
русским ученым Л.В. Ассуром, любой механизм может быть составлен
последовательным
присоединением
к
ведущему
звену
(звеньям)
кинематических цепей с нулевой степенью подвижности (групп Ассура).
Простейшая плоская группа Ассура представляет из себя
кинематическую цепь, состоящую из двух звеньев и трёх кинематических пар
V класса или из одного звена и кинематических пар IV-го и V-го классов.
12.
ВидВВВ
ВВП
Схема
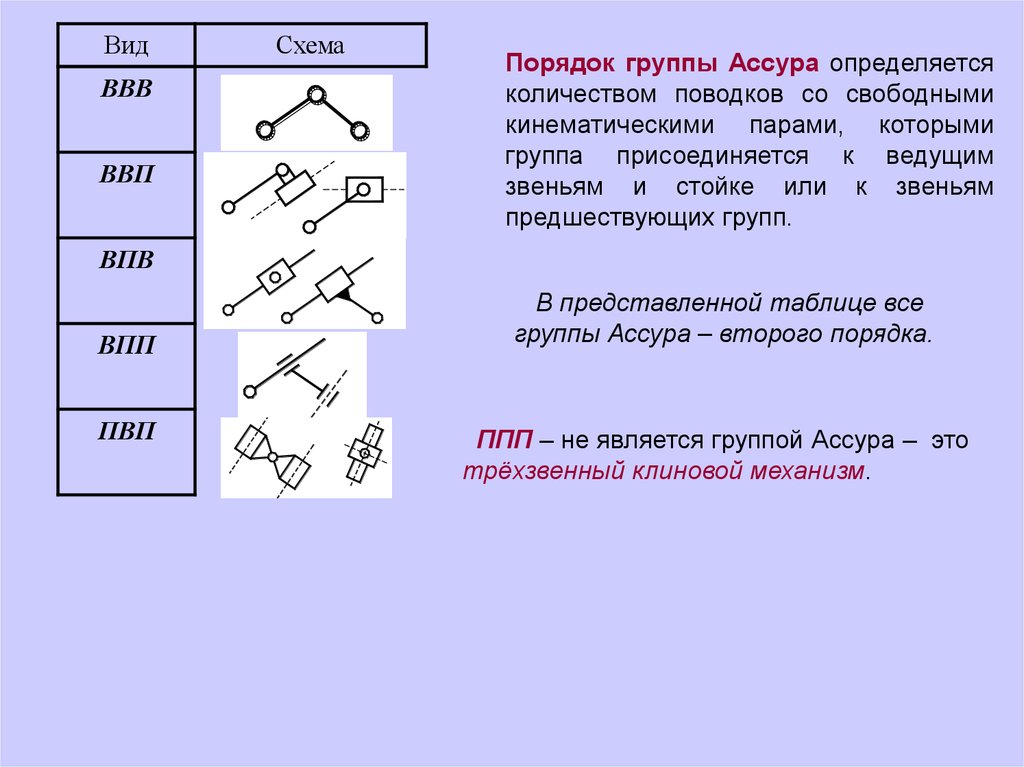
Порядок группы Ассура определяется
количеством поводков со свободными
кинематическими парами, которыми
группа присоединяется к ведущим
звеньям и стойке или к звеньям
предшествующих групп.
ВПВ
ВПП
ПВП
В представленной таблице все
группы Ассура – второго порядка.
ППП – не является группой Ассура – это
трёхзвенный клиновой механизм.
13.
Группы Ассура с кинематическими парами V-го и IV-го класса:а) кулачек -толкатель
б) зубчатое зацепление
Группы Ассура делятся на 4 класса:
1 класс. 2-х поводковая 2-го порядка, 3-х поводковая 3-го порядка, 4-х
поводковая 4-го порядка.
2 класс. Если хотя бы у одного 3-х шарнирного звена нет поводка.
3 класс. Если есть замкнутый контур нулевого порядка или 2-го порядка и т.д.
4 класс. Если есть 2 замкнутых контура.
14.
Подвижность плоских механизмовПодвижность или число степеней
определяют по формуле Чебышёва:
свободы
плоских
механизмов
w 3 n 1 2 p5 p4
, где n – количество звеньев, p5 - число КП 5-го класса, p4 - 4-го.
n-1 – число подвижных звеньев (т.к. подвижность стойки равна 0).
Пример. Если присоединим группу
Ассура
ВВВ
свободными
кинематическими парами к стойке
(рис.а), то подвижность:
w 3 (3 1) 2 3 0
Если группу Ассура ВВВ присоединить к ведущему звену 1, подвижность которого
равна w=1, и к стойке, то подвижность механизма не изменится (рис б).
w 3 4 1 2 4 1
15.
Разложение кинематической схемы механизма на группы Ассура и ведущее(начальное) звено называют структурным анализом.
Порядок структурного анализа механизма
1. Анализ реального механизма и составление его кинематической схемы
(плоской или пространственной).
2. Подсчет числа звеньев и кинематических пар (с учетом класса последних).
3. Определение степени подвижности механизма по формулам (1) и (2) и
анализ движения звеньев механизма.
4. Исключение (если это необходимо) пассивных связей и лишних степеней
свободы и проверка подвижности механизма по формулам (1) и (2).
5. Выделение начальных звеньев и групп Ассура.
6. Определение класса (порядок и вид) групп Ассура, названий звеньев и
кинематических пар.
16.
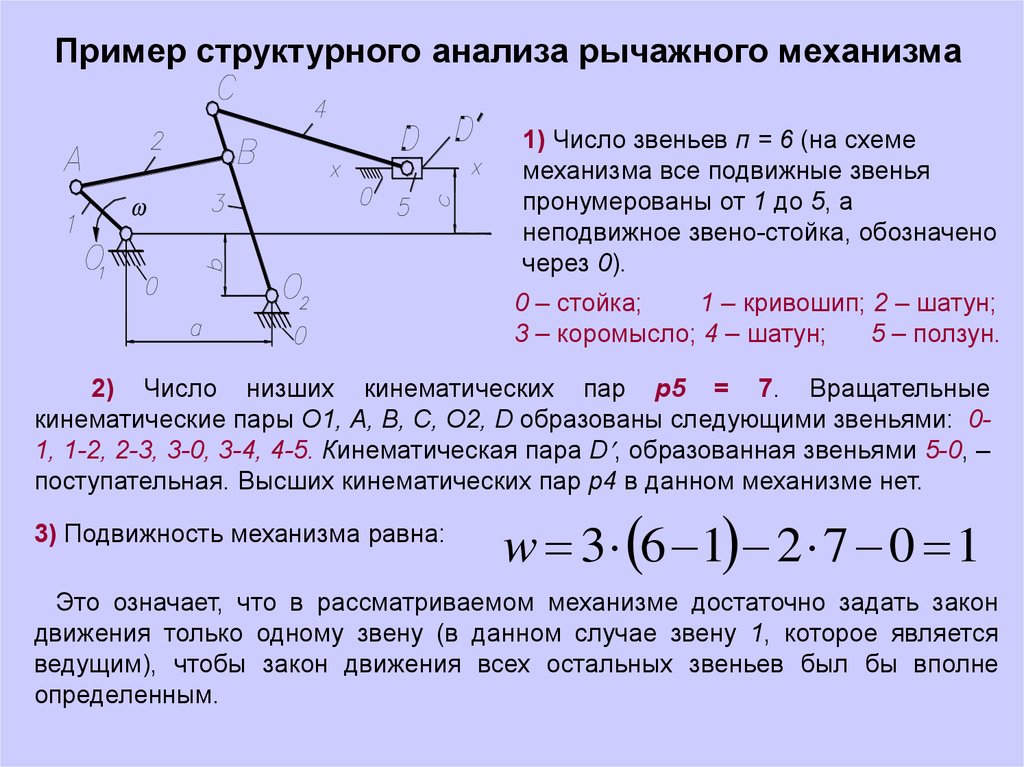
Пример структурного анализа рычажного механизма1) Число звеньев п = 6 (на схеме
механизма все подвижные звенья
пронумерованы от 1 до 5, а
неподвижное звено-стойка, обозначено
через 0).
0 – стойка;
1 – кривошип; 2 – шатун;
3 – коромысло; 4 – шатун;
5 – ползун.
2) Число низших кинематических пар р5 = 7. Вращательные
кинематические пары O1, A, B, C, O2, D образованы следующими звеньями: 01, 1-2, 2-3, 3-0, 3-4, 4-5. Кинематическая пара D , образованная звеньями 5-0, –
поступательная. Высших кинематических пар р4 в данном механизме нет.
3) Подвижность механизма равна:
w 3 6 1 2 7 0 1
Это означает, что в рассматриваемом механизме достаточно задать закон
движения только одному звену (в данном случае звену 1, которое является
ведущим), чтобы закон движения всех остальных звеньев был бы вполне
определенным.
17.
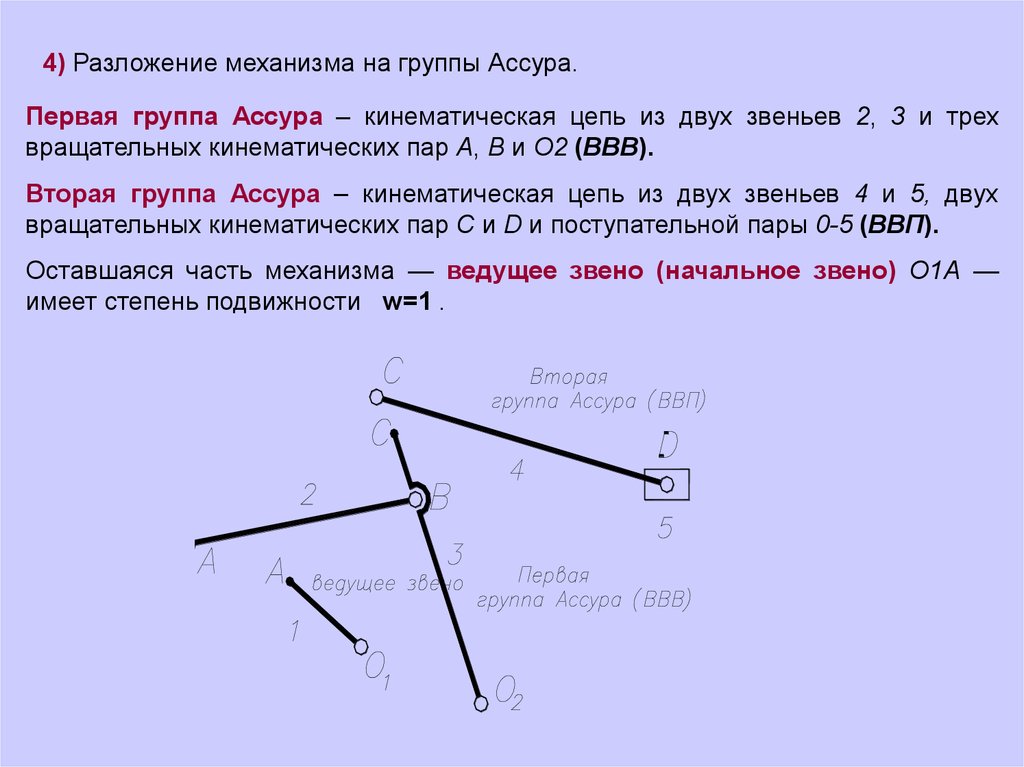
4) Разложение механизма на группы Ассура.Первая группа Ассура – кинематическая цепь из двух звеньев 2, 3 и трех
вращательных кинематических пар А, В и О2 (ВВВ).
Вторая группа Ассура – кинематическая цепь из двух звеньев 4 и 5, двух
вращательных кинематических пар С и D и поступательной пары 0-5 (ВВП).
Оставшаяся часть механизма — ведущее звено (начальное звено) О1А —
имеет степень подвижности w=1 .
18.
19.
2. КИНЕМАТИЧЕСКИЙ АНАЛИЗРЫЧАЖНЫХ МЕХАНИЗМОВ
2.1 Задачи и методы кинематического анализа
Задачи:
- определить положение звеньев механизма за цикл работы;
- траектории точек звеньев;
- угловые скорости и ускорения звеньев;
- линейные скорости и ускорения точек звеньев;
- годографы скоростей и ускорений точек;
- графики перемещений, скоростей и ускорений ползунов.
Методы:
1) Аналитические – точные, трудоемкие, с множеством
разных подходов (координатный, векторный и пр.).
2) Графические – имеют погрешности до 5 – 10%, просты в
реализации, наглядны.
3) Графоаналитические – методы, совмещающие 1) и 2).
4) Экспериментальные.
20.
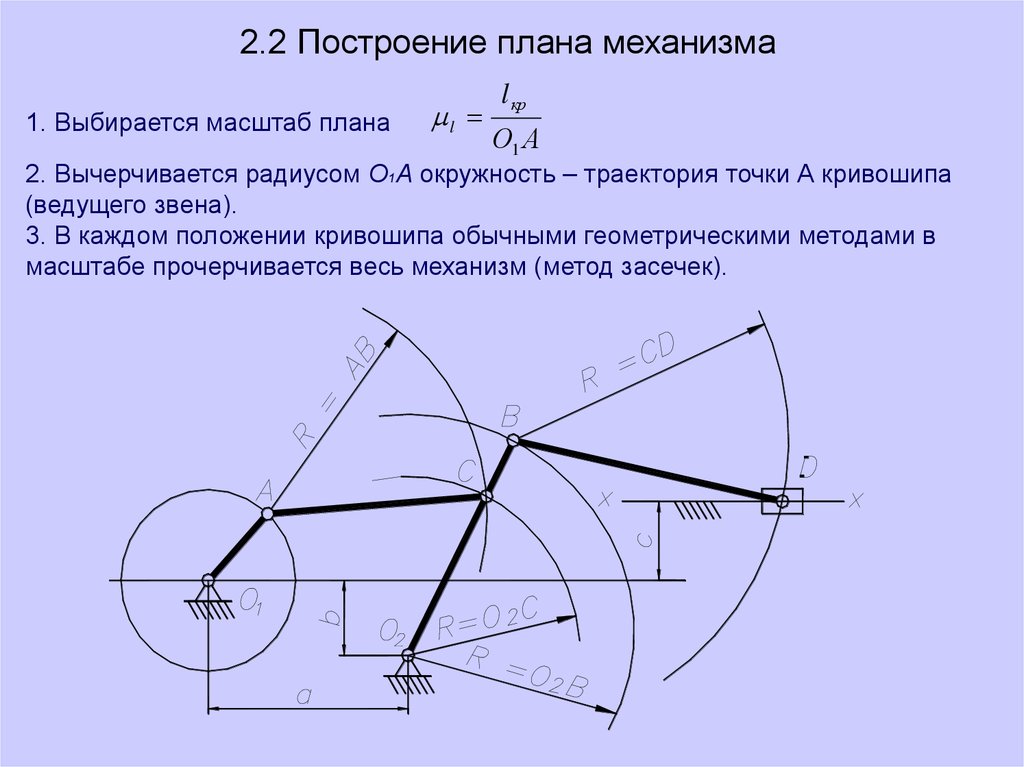
2.2 Построение плана механизма1. Выбирается масштаб плана
l
l кр
О1 А
2. Вычерчивается радиусом О1А окружность – траектория точки А кривошипа
(ведущего звена).
3. В каждом положении кривошипа обычными геометрическими методами в
масштабе прочерчивается весь механизм (метод засечек).
21.
2.3 Определение линейных скоростей точекзвеньев механизма
Построение плана скоростей начнём с ведущего звена О1А, которое
вращается относительно точки О1 с угловой скоростью ω1, равной:
n1 рад
1
(
)
с
30
Вектор абсолютной скорости точки А направлен перпендикулярно кривошипу,
в сторону его вращения, а модуль скорости определяется из выражения:
VA 1 lO1 A ( м )
с
Выбираем на плоскости произвольную точку р —
полюс плана скоростей, которая является началом
отсчета. Откладываем на ней вектор pa
(перпендикулярный к звену O1A в направлении
движения точки А).
м
V
VA
( с )
pa мм ч
Скорость О2 равна нулю, так как этот шарнир связан со стойкой.
Найдём скорость точки В. Точка В принадлежит одновременно двум звеньям –
2 и 3.
22.
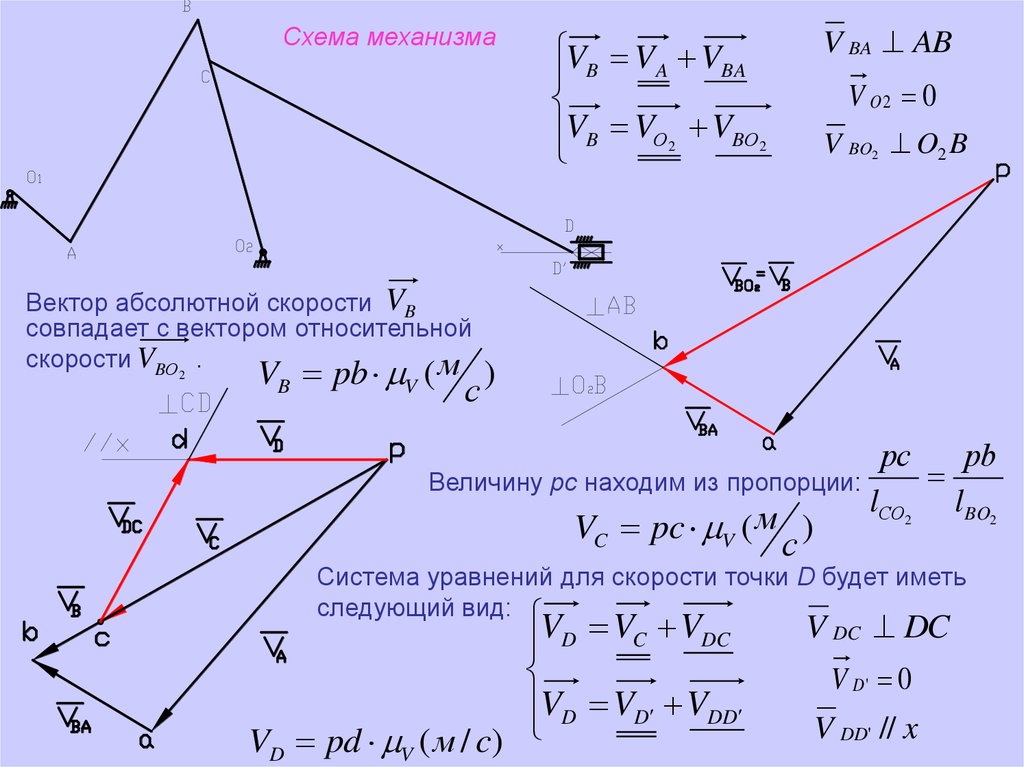
Схема механизмаВектор абсолютной скорости VB
совпадает с вектором относительной
скорости VBО2 .
м
VB pb V (
с
V BA AB
VB VA VBA
VB VО2 VBО2
V O2 0
V BO2 O2 B
)
Величину рс находим из пропорции:
VC pc V ( м )
с
рс
lСO2
рb
lBO2
Система уравнений для скорости точки D будет иметь
следующий вид:
VD VC VDC
VD VD VDD
VD pd V ( м / c)
V DC DC
V D' 0
V DD' // x
23.
!Все векторы скоростей, выходящие из полюса р – абсолютные, а все
векторы скоростей, не выходящие из полюса плана, – относительные.
2.4 Построение годографа скорости заданной точки
Годограф скорости – кривая, которая является геометрическим местом
точек конца вектора скорости. Годограф позволяет определить скорость точки в
любой момент времени по модулю и линии действия.
Для построения годографов скоростей и
ускорений точек механизма, совершающих
криволинейные движения нужно:
1) в выбранный полюс переместить вектора
скоростей или ускорений точки, взятые из
планов в одинаковом масштабе;
2) концы векторов соединит плавной кривой.
2.5 Определение угловых скоростей звеньев механизма
Угловые скорости звеньев можно определить, используя относительные
скорости построенного плана скоростей.
2
VBA ab V
( рад / с.)
l AB
l AB
3
VBO2
lBO2
VDC cd V
pb V
( рад / с.)
( рад / с.)
4
lCD
lCD
lBO2
24.
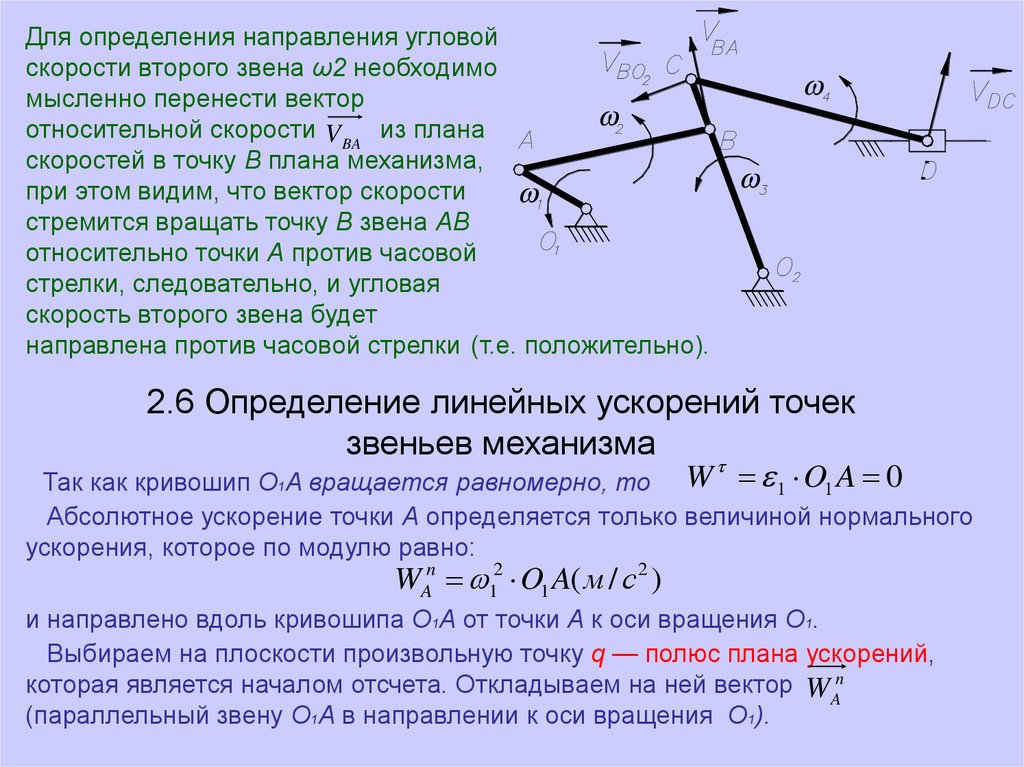
Для определения направления угловойскорости второго звена ω2 необходимо
мысленно перенести вектор
относительной скорости V BA из плана
скоростей в точку В плана механизма,
при этом видим, что вектор скорости
стремится вращать точку В звена АВ
относительно точки А против часовой
стрелки, следовательно, и угловая
скорость второго звена будет
направлена против часовой стрелки (т.е. положительно).
2.6 Определение линейных ускорений точек
звеньев механизма
Так как кривошип O A вращается равномерно, то W 1 O1 A 0
1
Абсолютное ускорение точки А определяется только величиной нормального
ускорения, которое по модулю равно:
WAn 12 O1 A( м / с 2 )
и направлено вдоль кривошипа O1A от точки А к оси вращения О1.
Выбираем на плоскости произвольную точку q — полюс плана ускорений,
которая является началом отсчета. Откладываем на ней вектор W An
(параллельный звену O1A в направлении к оси вращения O1).
25.
Масштабный коэффициентплана ускорений:
Схема механизма
WA м / с 2
W
(
)
qa мм ч
Определим
ускорение точки В.
W W W
B
A
BA
WB WO2 WBO2
Т.к. точка В движется криволинейно, то относительные
ускорения представим в виде суммы двух ускорений:
нормального и тангенциального.
2
W W W n W
A
BA
BA
B
n
W
WB WO2 WBO
BO2
2
n
WBA
n
WBO
2
WB qb W ( м / с 2 )
VBA
( м / с2 )
lBA
2
VBO
2
lBO2
( м / с2 )
26.
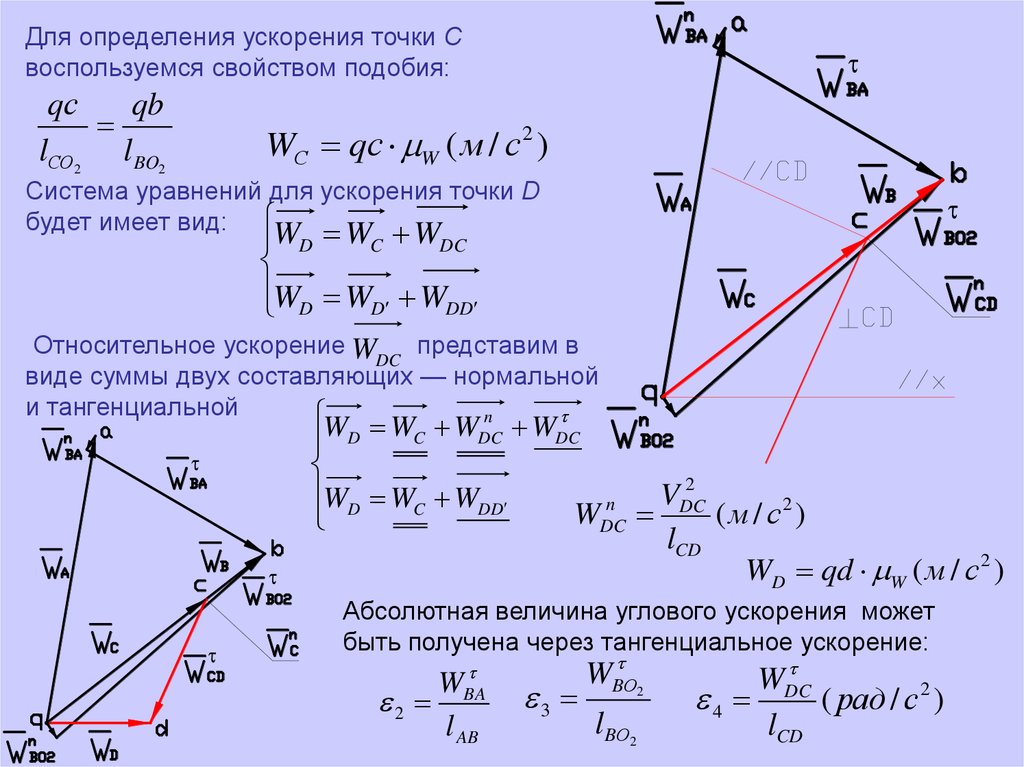
Для определения ускорения точки Cвоспользуемся свойством подобия:
qс
qb
lСO2 lBO2
WС qс W ( м / с 2 )
Система уравнений для ускорения точки D
будет имеет вид: W W W
D
C
DC
WD WD WDD
Относительное ускорение WDC представим в
виде суммы двух составляющих — нормальной
и тангенциальной
n
W WC WDC WDC
D
2
VDC
WD WC WDD
n
WDC
( м / с2 )
lCD
WD qd W ( м / с 2 )
Абсолютная величина углового ускорения может
быть получена через тангенциальное ускорение:
W
2 BA
l AB
3
WBО
2
lBО2
WDC
4
( рад / с 2 )
lCD
27.
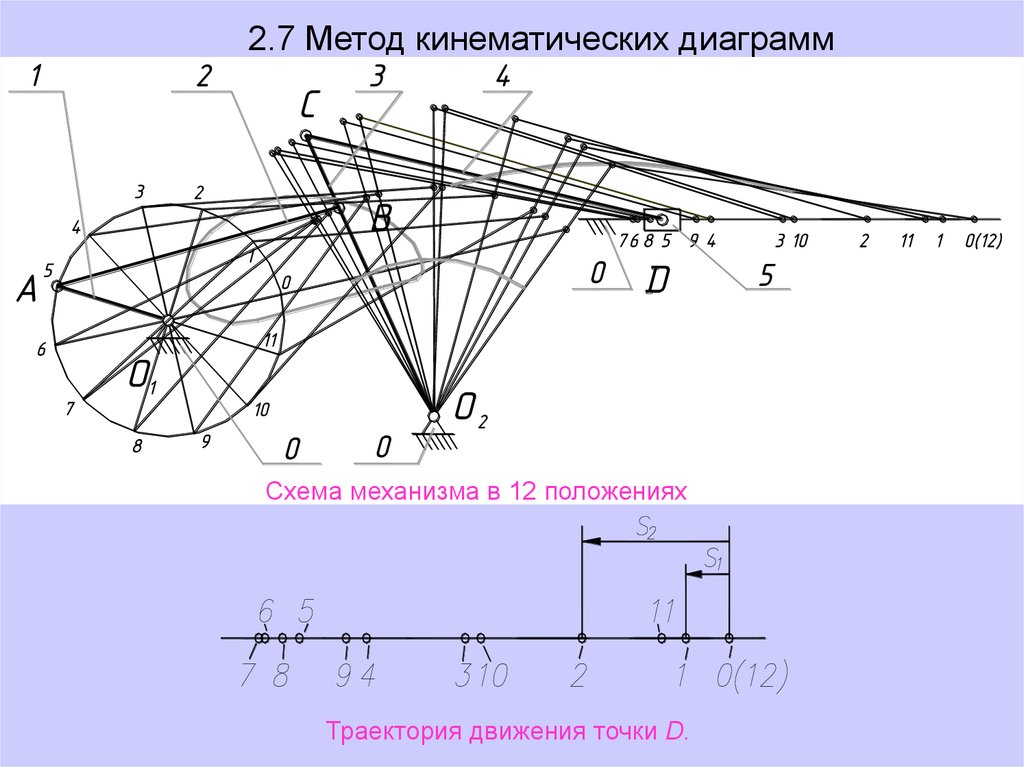
2.7 Метод кинематических диаграммСхема механизма в 12 положениях
Траектория движения точки D.
28.
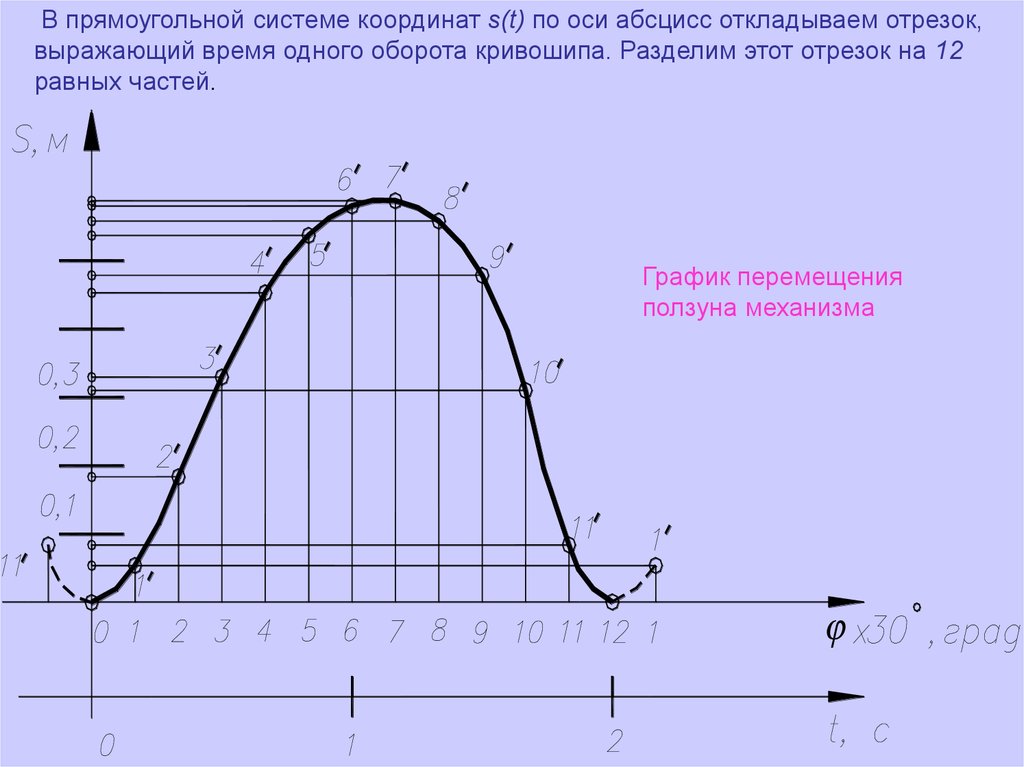
В прямоугольной системе координат ѕ(t) по оси абсцисс откладываем отрезок,выражающий время одного оборота кривошипа. Разделим этот отрезок на 12
равных частей.
График перемещения
ползуна механизма
29.
Построение диаграмм скоростей и ускоренийДиаграмма скорости точки D v(t)
строится путём графического
дифференцирования кривой
перемещения ѕ(t). Графическое
дифференцирование проводим
методом касательных.
Под диаграммой ѕ(t) проводим новую
систему координат v(t). На
продолжении оси Оφ влево строим
отрезок ОР1
В точках 1´, 2´… проводим
касательные к кривой ѕ(φ). Через
Р1 проводим лучи, параллельные
касательным. Эти лучи отсекут на
оси Оv отрезки 0-1´´, 0-2´´…
аналогичные скоростям в
соответствующих точках
диаграммы.
V
S
м/c
)
t OP1 мм ч
(
Диаграмму w(t) строим аналогично.
30.
Vм / c2
W
(
)
t OP2 мм ч
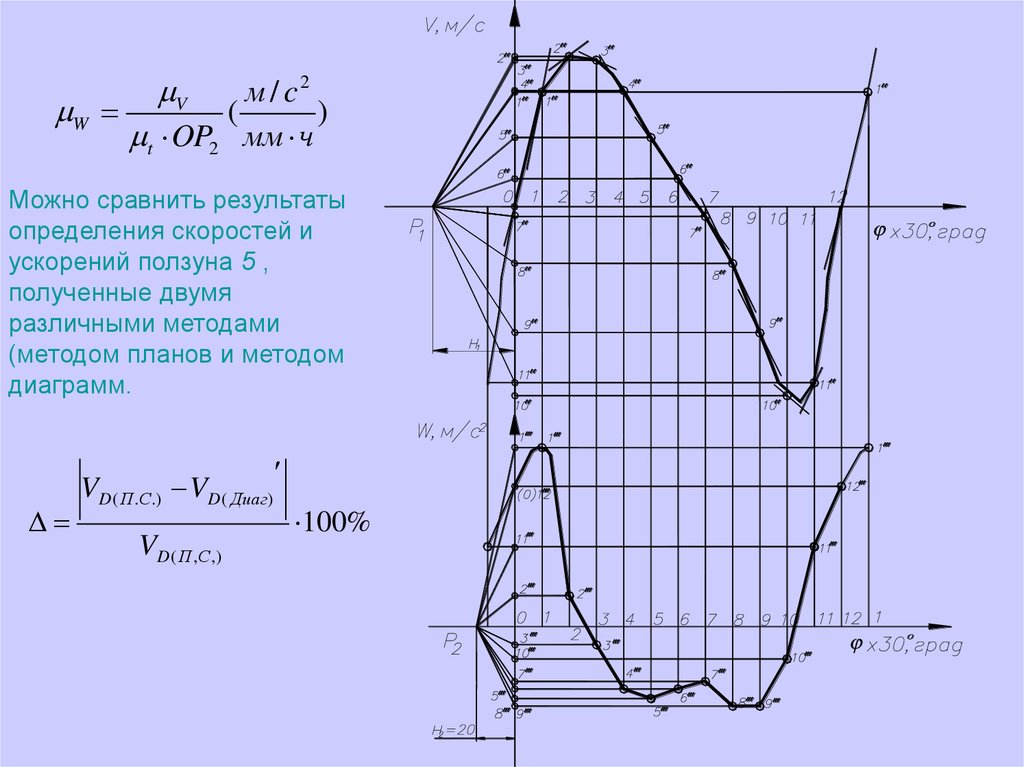
Можно сравнить результаты
определения скоростей и
ускорений ползуна 5 ,
полученные двумя
различными методами
(методом планов и методом
диаграмм.
VD ( П .С .) VD ( Диаг)
VD ( П ,С ,)
100%
31.
3. СИЛОВОЙ АНАЛИЗ РЫЧАЖНЫХ МЕХАНИЗМОВЗадачи:
- определить усилия в кинематических парах механизма;
- определить величину уравновешивающей силы (или момента).
Это необходимо для:
- расчёта звеньев механизма и элементов привода на прочность, устойчивость
и пр.;
- выбора типа и расчёта мощности привода;
- прогнозирования износа трущихся поверхностей;
- выбора типа подшипников и способа их смазки;
- расчёта к.п.д. механизма и решения большого числа других более мелких
вопросов конструирования механизма.
Механизмы бывают:
- Тихоходные – в которых силы инерции намного меньше, внешних сил и ими
можно пренебречь (проводится статический расчёт;
- Быстроходные – силы инерции больше некоторых внешних сил, которыми
в этом случае можно пренебречь (например, весом деталей).
Обычно силовой анализ выполняется с использованием принципа
Д'Аламбера. В этом случае такой расчёт (анализ) часто в литературе называют
кинетостатическим.
32.
Существует несколько видов (этапов, стадий) силового анализа механизма:А) Силовой анализ на начальном этапе.
На этом этапе для выполнения полезных функций создаётся кинематическая
схема механизма и на основании статистических данных выбираются некоторые
параметры звеньев и параметры работы его.
На этом этапе обычно предполагается, что начальное (ведущее) звено
механизма перемещается с постоянной скоростью 1 const . Это
предположение приводит к тому, что определяются несколько усреднённые
значения усилий в звеньях и кинематических парах. Но эти данные очень важны
для предварительной конструкторской проработки механизма: конструирования
звеньев механизма и кинематических пар; более точного определения весовых
и инерционных параметров звеньев; выполнения прочностных и иных расчётов
звеньев; выбора коэффициентов запаса прочности и т.д.
Б) Силовой анализ после предварительной конструкторской проработки.
Определённые новые значения параметров кинематической схемы
механизма учитываются при повторном кинематическом и силовом анализах
механизма, после чего, при необходимости, вносятся корректировки в
конструкцию механизма.
В) Силовой анализ после конструкторской разработки механизма.
На этом этапе по определённым правилам массы и моменты инерции всех
звеньев механизма приводятся к начальному звену, все внешние силы и
моменты также приводятся к начальному звену.
33.
Составляется дифференциальное уравнение движения начального звена(динамическая модель механизма), дважды интегрируя которое определяют
закон движения ведущего звена 1 var
Иногда на этом же этапе определяют параметры маховика, производят, если
это необходимо, уравновешивание некоторых звеньев. Затем вновь
производится кинематический и силовой анализ механизма и, при
необходимости, вносятся корректировки в конструкцию механизма.
Г) Если механизм предназначен для работы на борту летательного аппарата
или в условиях космоса, когда имеют место очень жёсткие ограничения на
габаритные размеры и массу, то задаются минимальные коэффициенты запаса
прочности и некоторые из рассмотренных этапов могут повторяться
многократно.
3.1 ПОРЯДОК ВЫПОЛНЕНИЯ СИЛОВОГО АНАЛИЗА
РЫЧАЖНОГО МЕХАНИЗМА
1) Определить весовые и инерционные параметры всех звеньев механизма.
2) Оценить рабочие нагрузки, действующие на механизм.
3) Начиная с последней группы Асура произвести силовой анализ групп в
направлении начального звена методом силовых многоугольников.
4) Выполнить силовой анализ начального звена и определить
уравновешивающую силу.
5) Построить «рычаг Жуковского» и произвести расчёт уравновешивающей
силы.
6) Сравнить значения уравновешивающей силы, найденные двумя методами.
34.
3.2 СИЛЫ, ДЕЙСТВУЮЩИЕ НА МЕХАНИЗМОсновными силами, определяющими характер движения механизма, являются
движущие силы, совершающие положительную работу, и силы полезного
(производственного) сопротивления, возникающие в процессе выполнения
механизмом полезной работы и совершающие отрицательную работу.
К движущим силам относятся: сила давления рабочей смеси на поршень
цилиндра двигателя внутреннего сгорания; момент, развиваемый
электродвигателем на ведущем валу насоса или компрессора, и т. д.
Силы полезного сопротивления — это те силы, для преодоления которых
предназначен механизм (силы сопротивления резанию в токарном станке,
сопротивления ткани проколу иглы в швейной машине и т. д.) Эти силы обычно
задаются в виде так называемых механических характеристик.
Механической характеристикой двигателя или рабочей машины
называют зависимость момента, приложенного к ведомому валу двигателя или к
ведущему валу рабочей машины, от одного или нескольких кинематических
параметров.
При работе механизма в результате действия всех приложенных к его звеньям
указанных сил в кинематических парах возникают реакции, которые
непосредственно не влияют на характер движения механизма, но на
поверхностях элементов кинематических пар вызывают силы трения. Эти силы
являются силами вредного сопротивления.
35.
Основная задача кинетостатического анализа (расчета) состоит вопределении реакций в кинематических парах механизмов или, иначе говоря,
давлений, возникающих в местах соприкосновения элементов кинематических
пар, а также в определении уравновешивающих моментов или
уравновешивающих сил.
3.3 СИЛЫ ИНЕРЦИИ
Система сил инерции звена, как и всякая плоская система сил, приложенная к
твердому телу, в общем случае приводится к одной силе Fи m WS
Эта сила приложена в центре тяжести звена S массой m и направленной в
сторону, противоположную направлению вектора WS ускорения центра тяжести
S звена, и к паре сил с моментом
М и J S
JS
– момент инерции звена относительно оси, проходящей через крайнюю
точку звена О и перпендикулярной плоскости движения.
Для того, чтобы найти
силу инерции звена АВ,
необходимо определить
ускорение середины этого
звена S AB из плана
ускорений
36.
При силовом расчете механизм расчленяется на отдельные группы Асура; приэтом силовой расчет начинается с группы, присоединенной последней в
процессе образования механизма, и заканчивается расчетом ведущего
(начального) звена механизма. Если плоский механизм имеет одну степень
свободы, то начальный механизм состоит из двух звеньев: неподвижного
(стойка) и начального звена. Эти звенья образуют либо вращательную
кинематическую пару (кривошип — стойка), либо поступательную
кинематическую пару (ползун — направляющие).
3.4 СИЛОВОЙ АНАЛИЗ ГРУППЫ АСУРА ВВП
На группу действуют
известные внешние
силы: силы тяжести
звеньев G 4 и G5 , силы
инерции F и и F5и ,
4
и
момент сил инерции М 4 ,
и сила полезного
сопротивления РС .
При выделении из механизма группы Асура или отдельного звена необходимо
действие отсоединённой части механизма нужно заменить реакциями связи,
приложенными к соответствующим элементам кинематических пар.
37.
Прикладываем неизвестные реакции R34 и R05 и составляем системууравнений равновесия исследуемой группы Асура:
F R R G F Р G F R 0
и
и
М
(
F
)
G
h
F
h
R
l
M
i
D ( зв4) 4 1 4 2 34 CD 4 0
l
М
(
F
)
R
h
G
0
2
F F G Р R R 0
i ( 4 5)
D
i ( зв 5 )
n
34
34
и
4
4
С
5
i ( зв 5 )
05
и
5
5
5
С
05
45
5
и
5
05
(1)
(2)
(3)
(4)
R34
можно получить из
уравнения равновесия (2)
составленного для звена 4
относительно шарнира D.
Уравнение (1) можно решить
графически методом
построения плана сил.
38.
Из уравнения (3) найдём точку приложения реакциирасстоянии h от шарнира D:
G5 l5
h
R 05 находящейся на
R05 2
Для определения реакции R 45 звена
4 на звено 5 воспользуемся
уравнением равновесия сил,
действующих на звено 5 в векторном
виде (4), вычертив соответствующий
силовой многоугольник.
3.5 СИЛОВОЙ АНАЛИЗ ГРУППЫ АСУРА ВВВ
На группу действуют известные внешние силы: силы тяжести звеньев G 2
и G3 , силы инерции F2и и F3и , моменты сил инерции М 2и и М 3и .
Реакция в точке С со стороны группы Асура 4-5 уже известна по модулю и
направлению, т.к.
R43 R34
39.
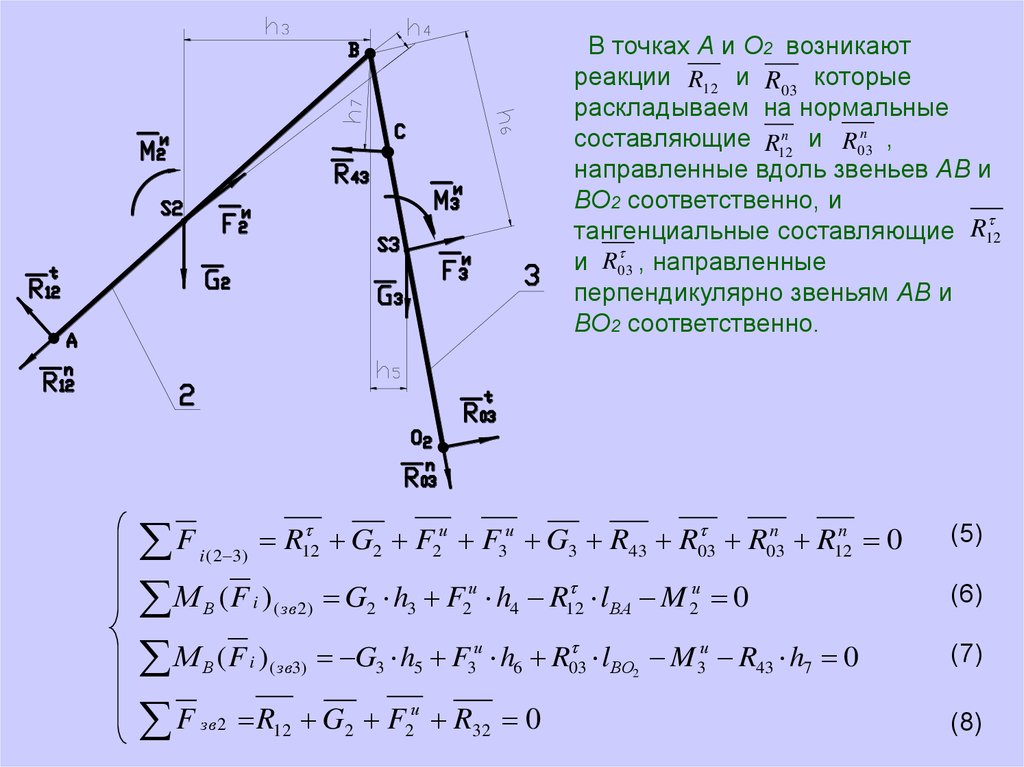
В точках А и О2 возникаютреакции R12 и R03 которые
раскладываем на нормальные
составляющие R12n и R03n ,
направленные вдоль звеньев АВ и
ВО2 соответственно, и
тангенциальные составляющие R12
и R03
, направленные
перпендикулярно звеньям АВ и
ВО2 соответственно.
F
М
М
F
i ( 2 3)
В
n
R12
G2 F2и F3и G3 R43 R03
R03
R12n 0
( F i ) ( зв 2) G2 h3 F2и h4 R12
l ВА M 2и 0
и
и
(
F
)
G
h
F
h
R
l
M
i
В
( зв3)
3
5
3
6
03 ВО2
3 R43 h7 0
зв 2
R12 G2 F2и R32 0
(5)
(6)
(7)
(8)
40.
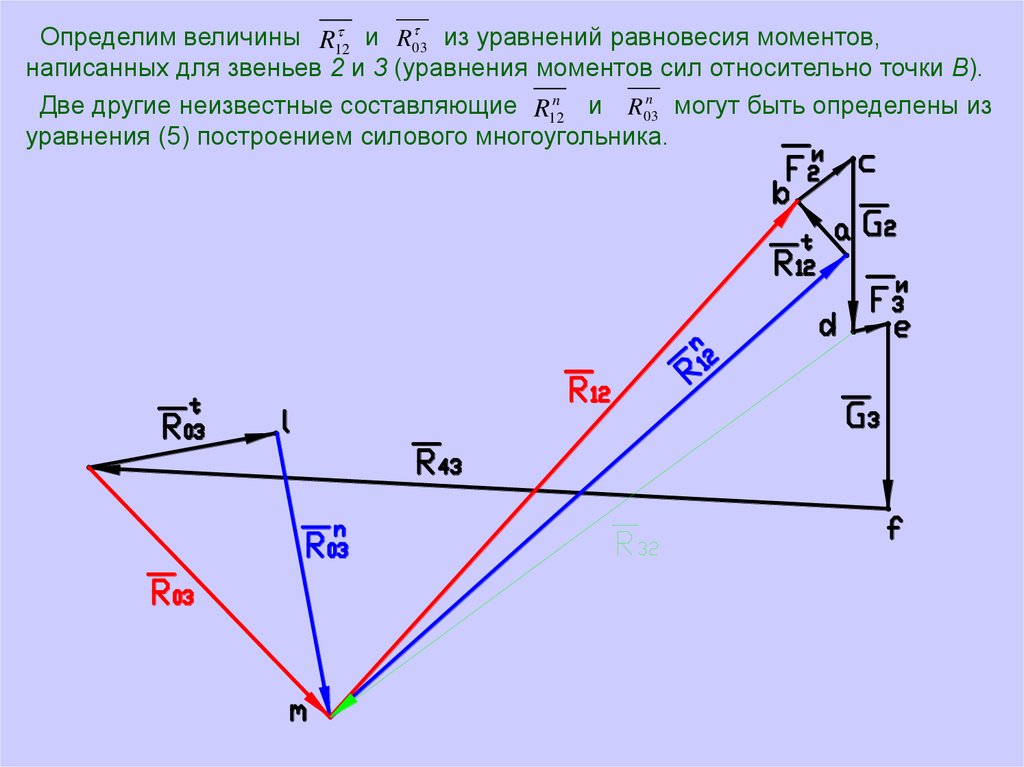
Определим величины R12и R03
из уравнений равновесия моментов,
написанных для звеньев 2 и 3 (уравнения моментов сил относительно точки В).
Две другие неизвестные составляющие R12n и R03n могут быть определены из
уравнения (5) построением силового многоугольника.
41.
3.6 СИЛОВОЙ АНАЛИЗ НАЧАЛЬНОГО ЗВЕНАЗвено 1 равномерно вращается вокруг оси, проходящей через его центр масс.
На звено 1 действуют внешняя сила R21 R12 и вес звена G1 .
Чтобы начальное звено находилось в равновесии, необходимо
дополнительно ввести силу, уравновешивающую все силы, приложенные к
ведущему звену.
Уравновешивающую силу F у прикладываем перпендикулярно кривошипу в
шарнире А.
M О ( F ) R21 h8 FУ АО1 0 (9)
F
1
i ( зв1)
i
R 21 G1 F у R 01 0
(10)
Величину уравновешивающей силы определяем
из уравнения (9):
h8
Fу R21
l AО1
Если кривошип приводится во вращение парой,
например, непосредственно от электродвигателя,
то в этом случае к валу приложен
уравновешивающий момент, который можно
определить из уравнения: M F l
y
У
Реакцию R01 можно получить построением силового
многоугольника.
AО1
42.
3.7 РЫЧАГ Н.Е. ЖУКОВСКОГООпределить уравновешивающую силу FУ можно рассматривая механизм в
целом, не расчленяя его на группы Асура и не определяя реакций внутренних
связей. Метод основан на принципе возможных перемещений.
Для системы, обладающей стационарными связями, возможные
перемещения совпадают с действительными элементарными перемещениями.
Математическое выражение принципа возможных перемещений в этом случае
получает такой вид:
n
n
P s
i
i
cos( Pi si ) Ai 0
1
или, разделив на dt:
1
n
P V cos( P V ) N
i
1
Предположим, что в
точке I звена АВ
приложена сила Pi
перенесенная
параллельно самой
себе в изображающую
точку i повернутого на
90° плана скоростей
звена.
n
i
i
i
1
i
0
43.
МощностьNi
силы
Pi
можно выразить следующим образом:
N i Pi Vi cos i Pi pi v cos i Pi hi v
hi
— перпендикуляр, опущенный из полюса р плана скоростей на линию
действия силы.
Так как полученное выше уравнение, определяющее величину N i , имеет
место для всех сил Pi действующих на другие звенья механизма, то будем
n
n
иметь:
N
Поскольку v 0 , то
i
v Pi hi 0
1
1
n
P h
i
i
0
1
На этом основан метод рычага Жуковского.
Для рассматриваемого механизма строится план скоростей и поворачивается
на 90° в сторону вращения кривошипа. В соответствующих точках плана
скоростей прикладываются внешние силы. Полученный чертёж рассматриваем
как жёсткий рычаг, вращающийся вокруг полюса р (рычаг Жуковского). Записав
уравнение равновесия рычага найдём уравновешивающую силу
.
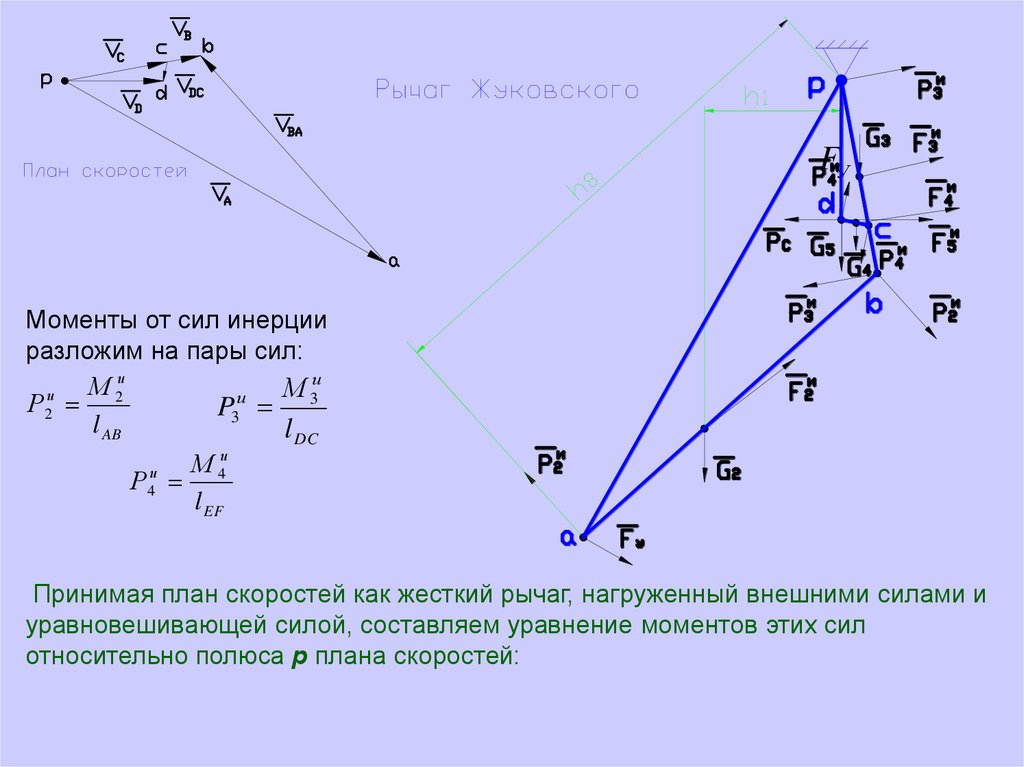
44.
FУМоменты от сил инерции
разложим на пары сил:
М 2и
М 3и
и
и
Р2
P3
l AB
l DC
М 4и
Р
l EF
и
4
Принимая план скоростей как жесткий рычаг, нагруженный внешними силами и
уравновешивающей силой, составляем уравнение моментов этих сил
относительно полюса р плана скоростей:
45.
иМ
(
F
)
G
h
G
h
G
h
(
F
i
р
2
1
3
2
4
3
5 PC ) pf
F3и h4 F4и h5 F2и h6 Р3и h7 P2и h8 P2и h9
P4и h10 P4и h11 FУ рa 0
Из этого уравнения определяем величину уравновешивающей силы:
( PC F5и ) pf G2 h1 G3 h2 G4 h3 F3и h4
FУ
ра
F4и h5 F2и h6 Р3и h7 P2и h8 P2и h9 P4и h10 P2и h11
pа
Метод рычага Жуковского является более точным, т.к. погрешность
построений не накапливается, как в методе планов сил.
Метод планов позволяет определить не только уравновешивающую силу, но
и реакции в связях механизма, что важно знать при дальнейшем
конструировании и расчёте механизма и его элементов.
Сравним значения уравновешивающей силы, полученные двумя методами:
FУ ( Р. Ж .) FУ ( пл)
FУ ( Р. Ж .)
100%
46.
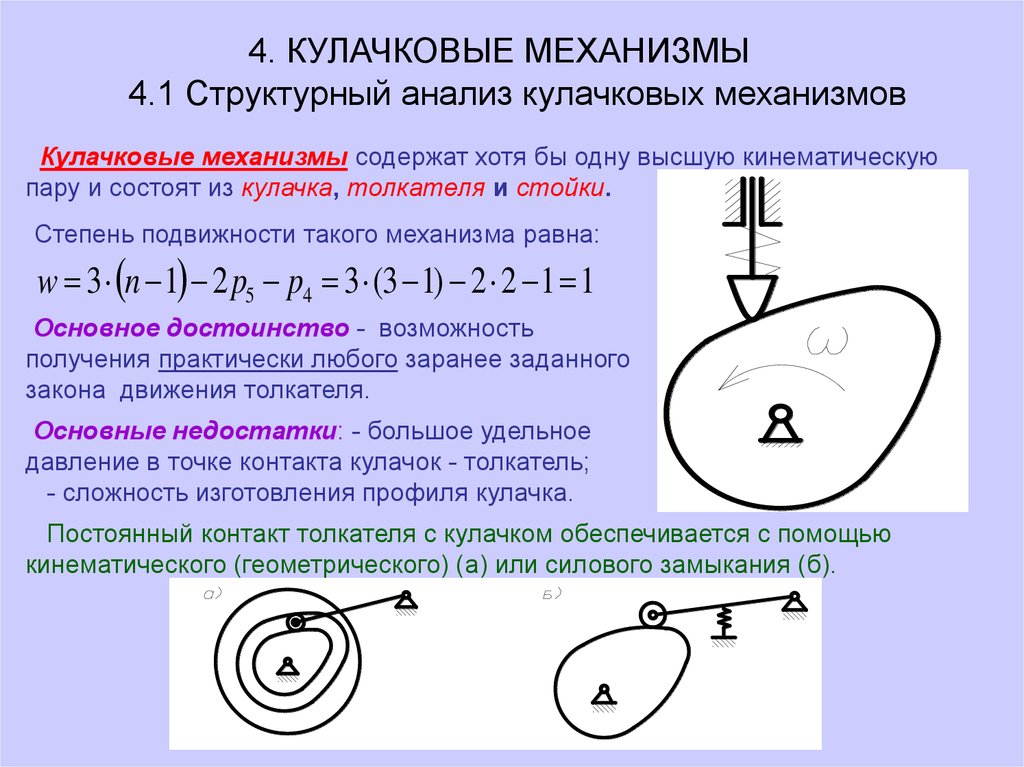
4. КУЛАЧКОВЫЕ МЕХАНИЗМЫ4.1 Структурный анализ кулачковых механизмов
Кулачковые механизмы содержат хотя бы одну высшую кинематическую
пару и состоят из кулачка, толкателя и стойки.
Степень подвижности такого механизма равна:
w 3 n 1 2 p5 p4 3 (3 1) 2 2 1 1
Основное достоинство - возможность
получения практически любого заранее заданного
закона движения толкателя.
Основные недостатки: - большое удельное
давление в точке контакта кулачок - толкатель;
- сложность изготовления профиля кулачка.
Постоянный контакт толкателя с кулачком обеспечивается с помощью
кинематического (геометрического) (а) или силового замыкания (б).
47.
Кулачковые механизмы могут быть плоскими и пространственными,центральными (е=0) и смещёнными (е≠0, выше к.п.д., но больше габариты).
Толкатели могут быть стержневые
и коромысловые.
Точка контакта толкателя с кулачком
конструктивно может быть выполнена:
заострённой, тарельчатой или
роликовой.
Разные схемы кулачковых
механизмов:
48.
Широко применяются:- машиностроение, приборостроение;
- сложные технологические машины
(текстильные, полиграфические и пр.);
- механические счётно-решающие
устройства;
- ДВС.
49.
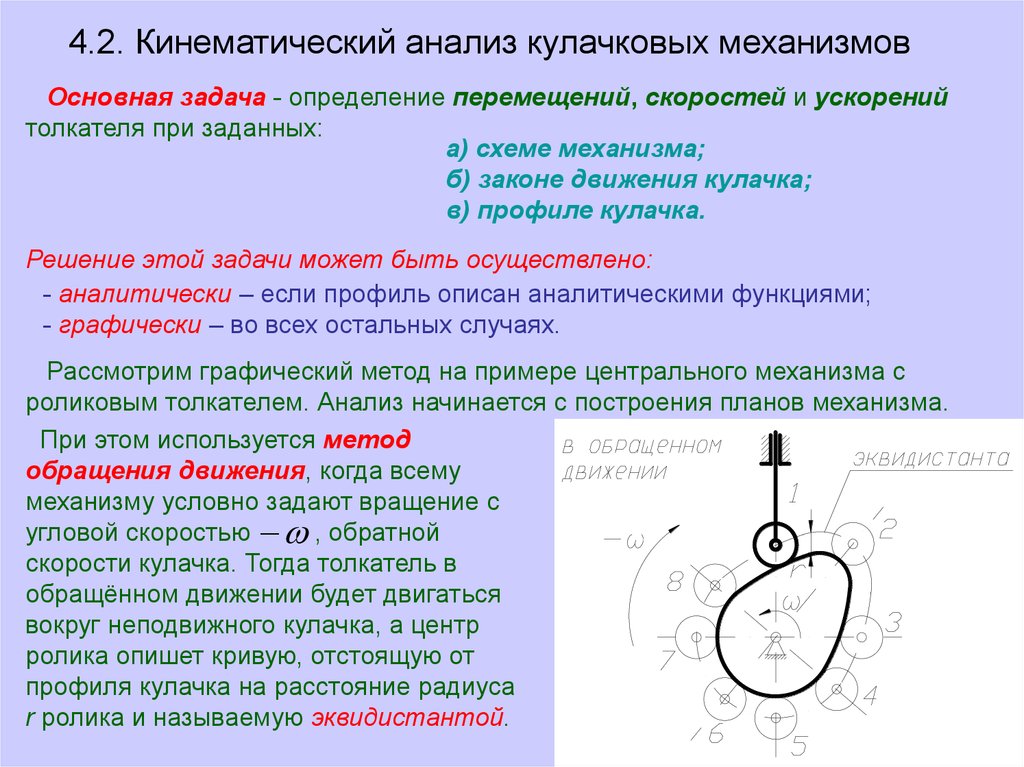
4.2. Кинематический анализ кулачковых механизмовОсновная задача - определение перемещений, скоростей и ускорений
толкателя при заданных:
а) схеме механизма;
б) законе движения кулачка;
в) профиле кулачка.
Решение этой задачи может быть осуществлено:
- аналитически – если профиль описан аналитическими функциями;
- графически – во всех остальных случаях.
Рассмотрим графический метод на примере центрального механизма с
роликовым толкателем. Анализ начинается с построения планов механизма.
При этом используется метод
обращения движения, когда всему
механизму условно задают вращение с
угловой скоростью , обратной
скорости кулачка. Тогда толкатель в
обращённом движении будет двигаться
вокруг неподвижного кулачка, а центр
ролика опишет кривую, отстоящую от
профиля кулачка на расстояние радиуса
r ролика и называемую эквидистантой.
50.
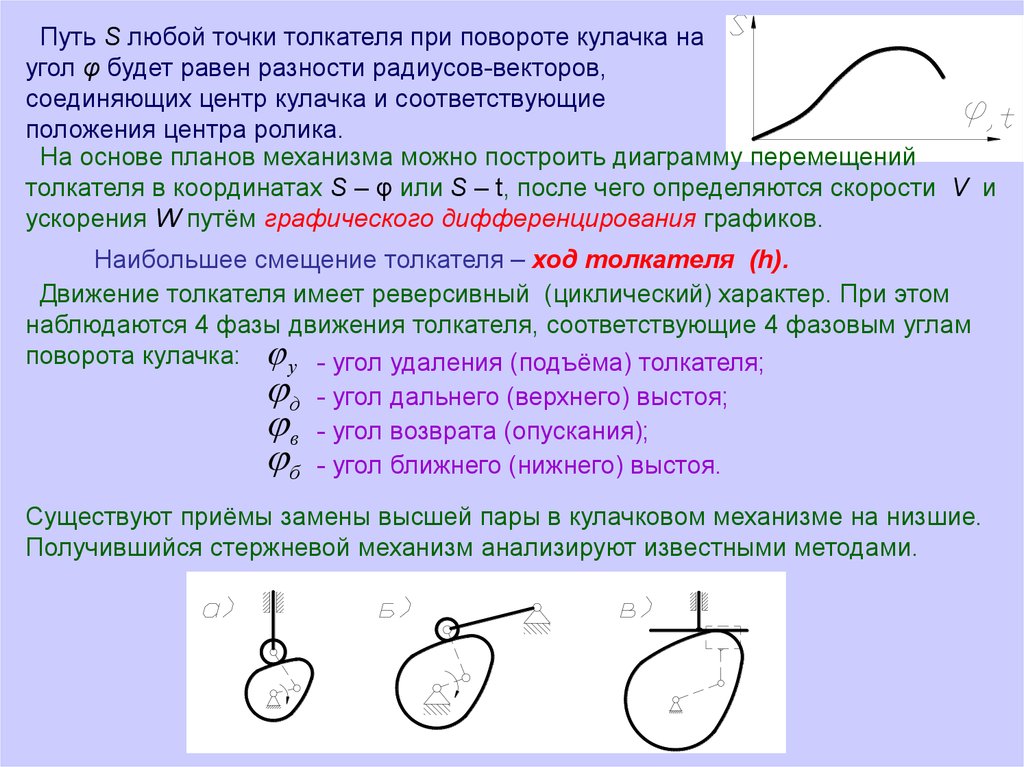
Путь S любой точки толкателя при повороте кулачка наугол φ будет равен разности радиусов-векторов,
соединяющих центр кулачка и соответствующие
положения центра ролика.
На основе планов механизма можно построить диаграмму перемещений
толкателя в координатах S – φ или S – t, после чего определяются скорости V и
ускорения W путём графического дифференцирования графиков.
Наибольшее смещение толкателя – ход толкателя (h).
Движение толкателя имеет реверсивный (циклический) характер. При этом
наблюдаются 4 фазы движения толкателя, соответствующие 4 фазовым углам
поворота кулачка: у - угол удаления (подъёма) толкателя;
д - угол дальнего (верхнего) выстоя;
в - угол возврата (опускания);
б - угол ближнего (нижнего) выстоя.
Существуют приёмы замены высшей пары в кулачковом механизме на низшие.
Получившийся стержневой механизм анализируют известными методами.
51.
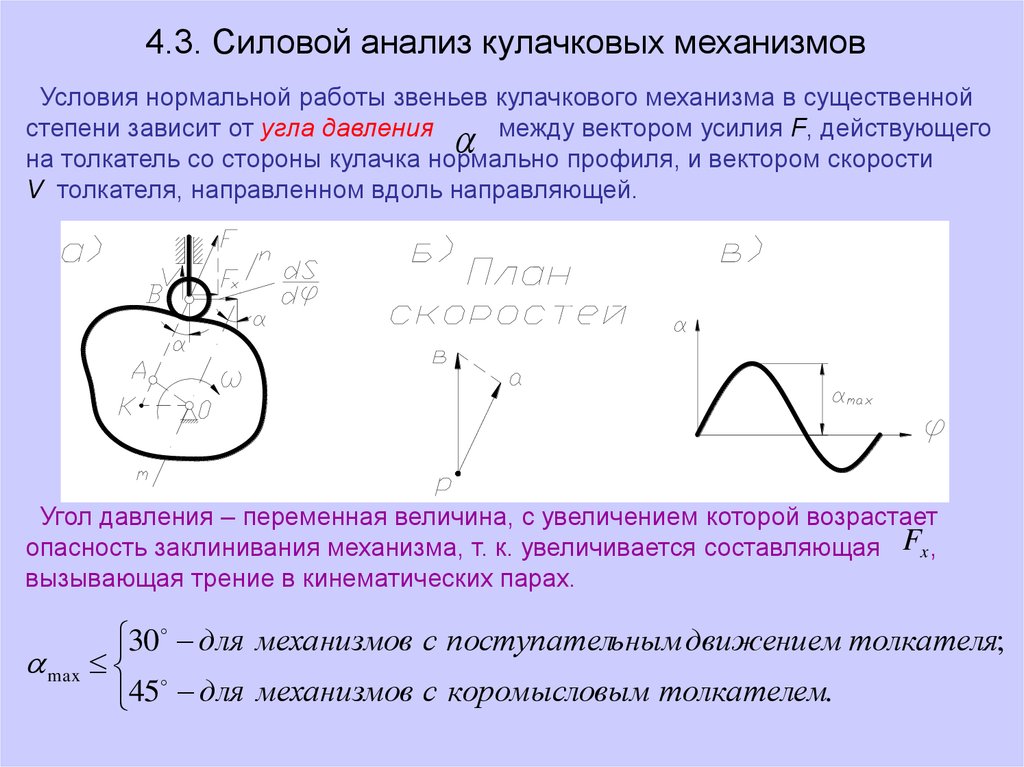
4.3. Силовой анализ кулачковых механизмовУсловия нормальной работы звеньев кулачкового механизма в существенной
степени зависит от угла давления
между вектором усилия F, действующего
на толкатель со стороны кулачка нормально профиля, и вектором скорости
V толкателя, направленном вдоль направляющей.
Угол давления – переменная величина, с увеличением которой возрастает
опасность заклинивания механизма, т. к. увеличивается составляющая Fx ,
вызывающая трение в кинематических парах.
30 для механизмов с поступательным движением толкателя;
max
45 для механизмов с коромысловым толкателем.
52.
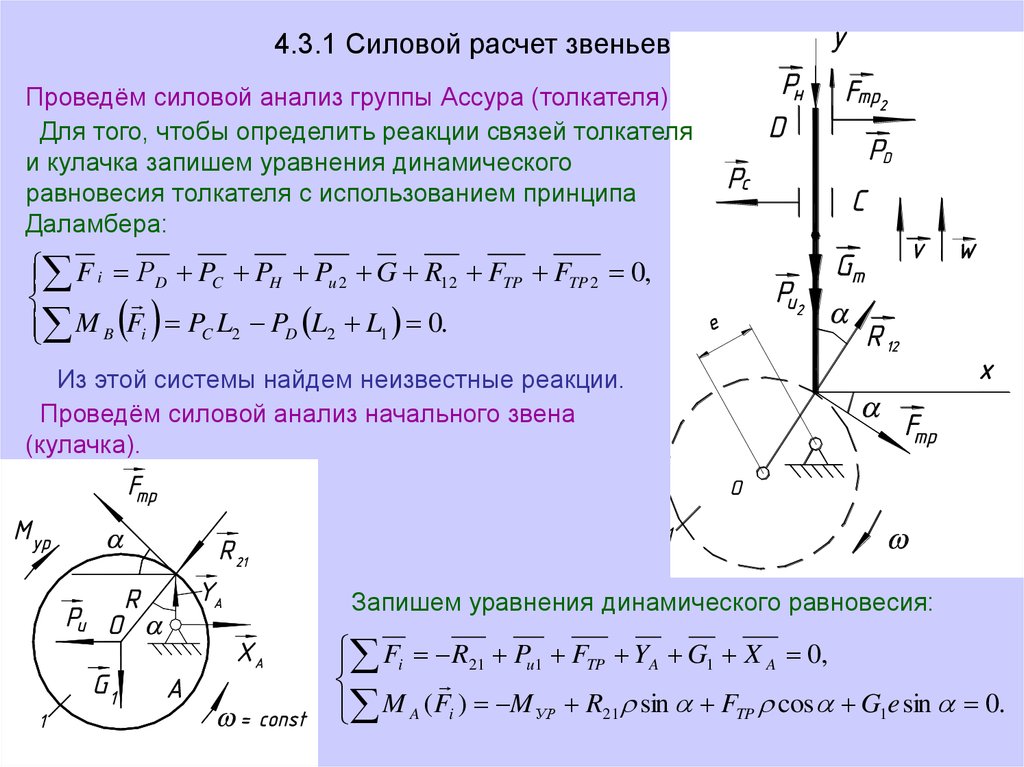
4.3.1 Силовой расчет звеньевПроведём силовой анализ группы Ассура (толкателя).
Для того, чтобы определить реакции связей толкателя
и кулачка запишем уравнения динамического
равновесия толкателя с использованием принципа
Даламбера:
F i РD PC PH Pu 2 G R12 FTP FTP 2 0,
M B Fi PC L2 PD L2 L1 0.
Из этой системы найдем неизвестные реакции.
Проведём силовой анализ начального звена
(кулачка).
Запишем уравнения динамического равновесия:
Fi R21 Pu1 FTP YA G1 X A 0,
M A ( Fi ) M УР R21 sin FTP cos G1e sin 0.
53.
4.4. Синтез кулачковых механизмовПри синтезе кулачковых механизмов необходимо решить следующие задачи:
- выбрать кинематическую схему механизма;
- выбрать (обосновать) закон движения толкателя.
(обычно из конструктивных или технологических соображений (ограничений)).
- рассчитать или выбрать основные размеры звеньев;
- построить профиль кулачка.
Некоторые рекомендации по выбору профиля:
1. Если нет особых требований на закон движения – применяется кулачёкэксцентрик h = 2 e - такая задача легко решается аналитически.
2. Условие – вход толкателя на профиль должен быть безударным выбирается закон движения по синусоиде или по параболе.
3. Условие – быстрое смещение толкателя в верхнее положение (ДВС)
- закон косинуса – начало движения – мягкий удар.
4. Условий много. Профиль кулачка составляется из нескольких кривых кривые «сшиваются» по скорости (мягкие удары) или по ускорению (без
ударов).
Динамический синтез минимального радиуса кулачка
Пусть заданы закон движения толкателя и предельно допустимый угол
давления доп
54.
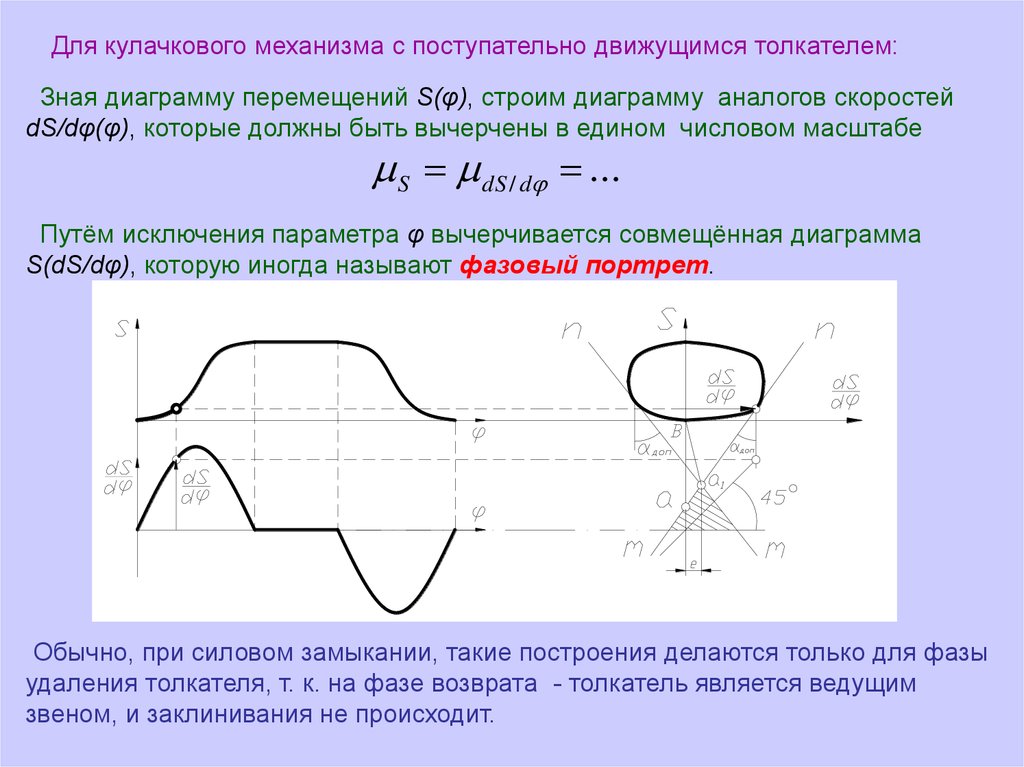
Для кулачкового механизма с поступательно движущимся толкателем:Зная диаграмму перемещений S(φ), строим диаграмму аналогов скоростей
dS/dφ(φ), которые должны быть вычерчены в едином числовом масштабе
S dS / d ...
Путём исключения параметра φ вычерчивается совмещённая диаграмма
S(dS/dφ), которую иногда называют фазовый портрет.
Обычно, при силовом замыкании, такие построения делаются только для фазы
удаления толкателя, т. к. на фазе возврата - толкатель является ведущим
звеном, и заклинивания не происходит.
55.
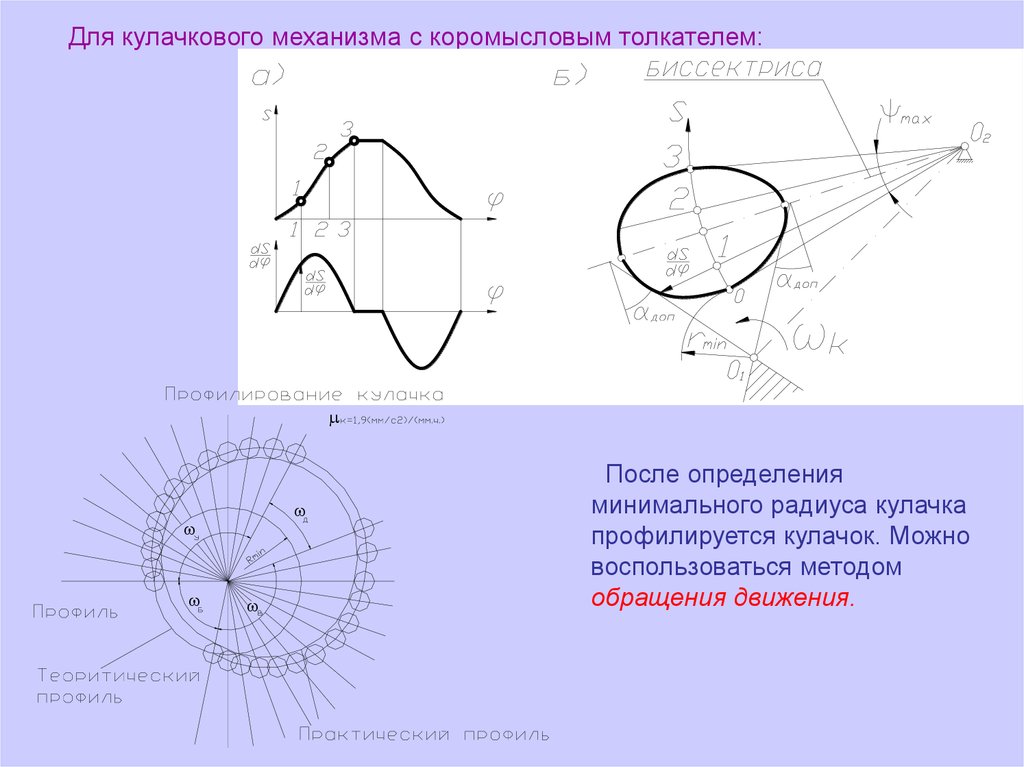
Для кулачкового механизма с коромысловым толкателем:После определения
минимального радиуса кулачка
профилируется кулачок. Можно
воспользоваться методом
обращения движения.
56.
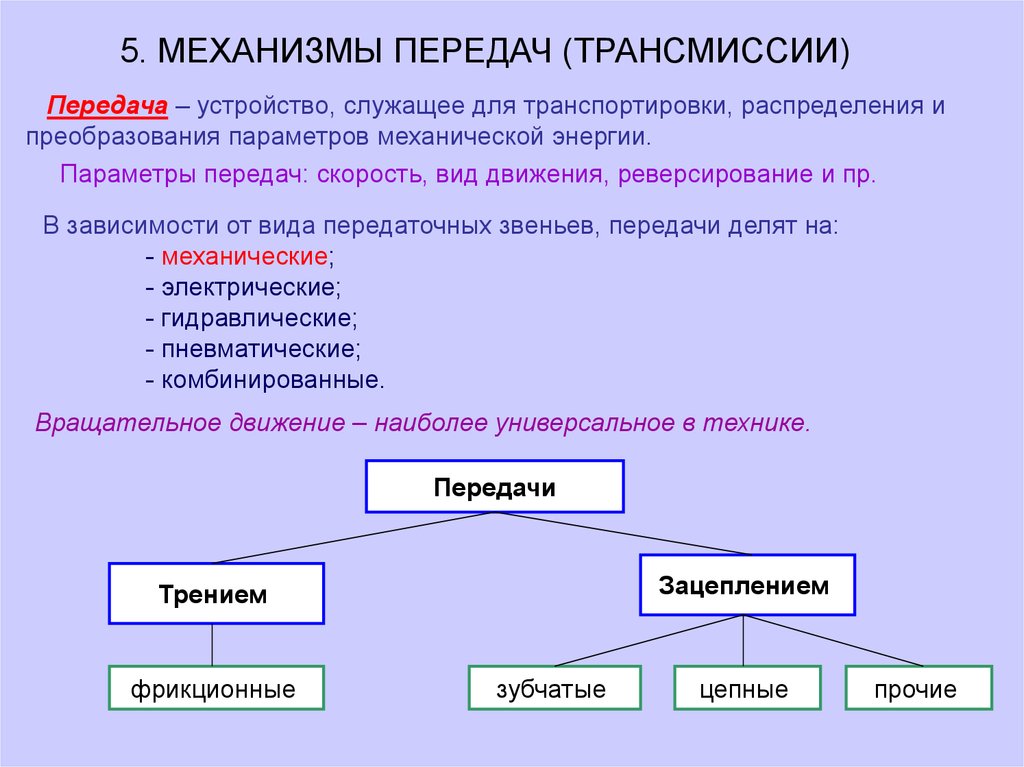
5. МЕХАНИЗМЫ ПЕРЕДАЧ (ТРАНСМИССИИ)Передача – устройство, служащее для транспортировки, распределения и
преобразования параметров механической энергии.
Параметры передач: скорость, вид движения, реверсирование и пр.
В зависимости от вида передаточных звеньев, передачи делят на:
- механические;
- электрические;
- гидравлические;
- пневматические;
- комбинированные.
Вращательное движение – наиболее универсальное в технике.
Передачи
Зацеплением
Трением
фрикционные
зубчатые
цепные
прочие
57.
5.1. Фрикционные передачи (ФП)Достоинства: - плавность хода;
- бесшумность;
- простота конструкции.
Недостатки: - ограничение по мощности;
- не высокий к.п.д. (0,8 – 0,9);
- высокие нагрузки на валы и подшипники;
- нестабильность параметров.
Фрикционные материалы:
- текстолит;
- фибра;
- резина;
- металлокерамика;
- кожа;
- дерево.
5.1.1 Структура ФП
ФП
С жесткими звеньями
Катковые
С гибкими звеньями
Ремённые
Канатные
58.
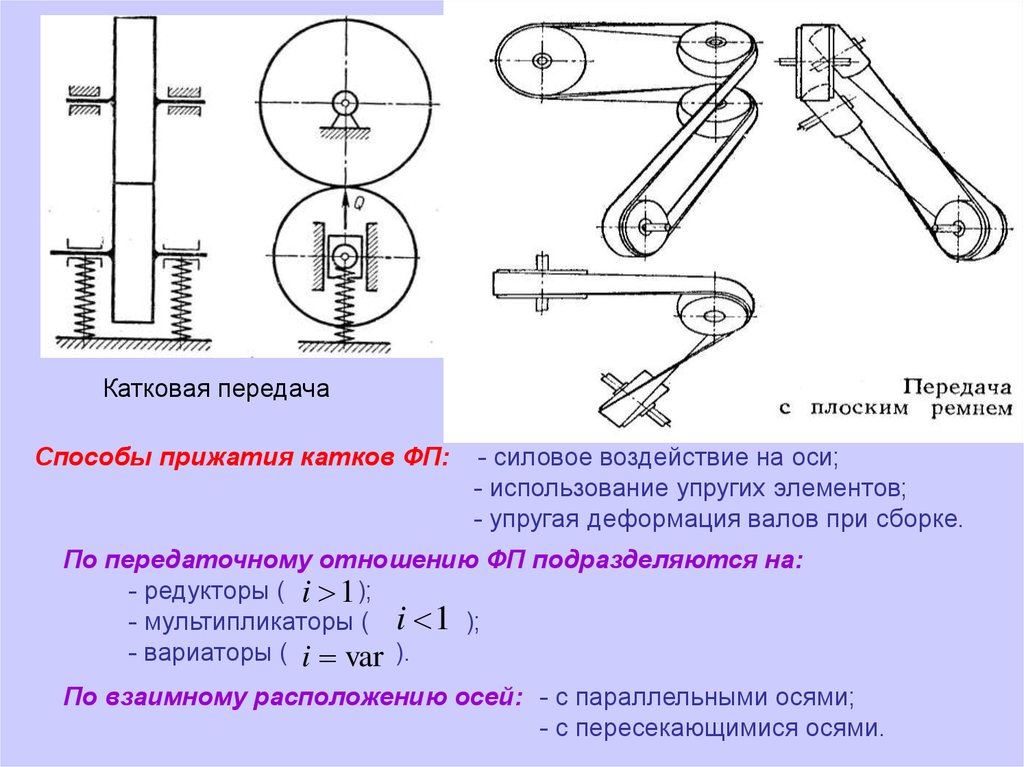
Катковая передачаСпособы прижатия катков ФП:
- силовое воздействие на оси;
- использование упругих элементов;
- упругая деформация валов при сборке.
По передаточному отношению ФП подразделяются на:
- редукторы ( i 1 );
- мультипликаторы ( i 1 );
- вариаторы ( i var ).
По взаимному расположению осей: - с параллельными осями;
- с пересекающимися осями.
59.
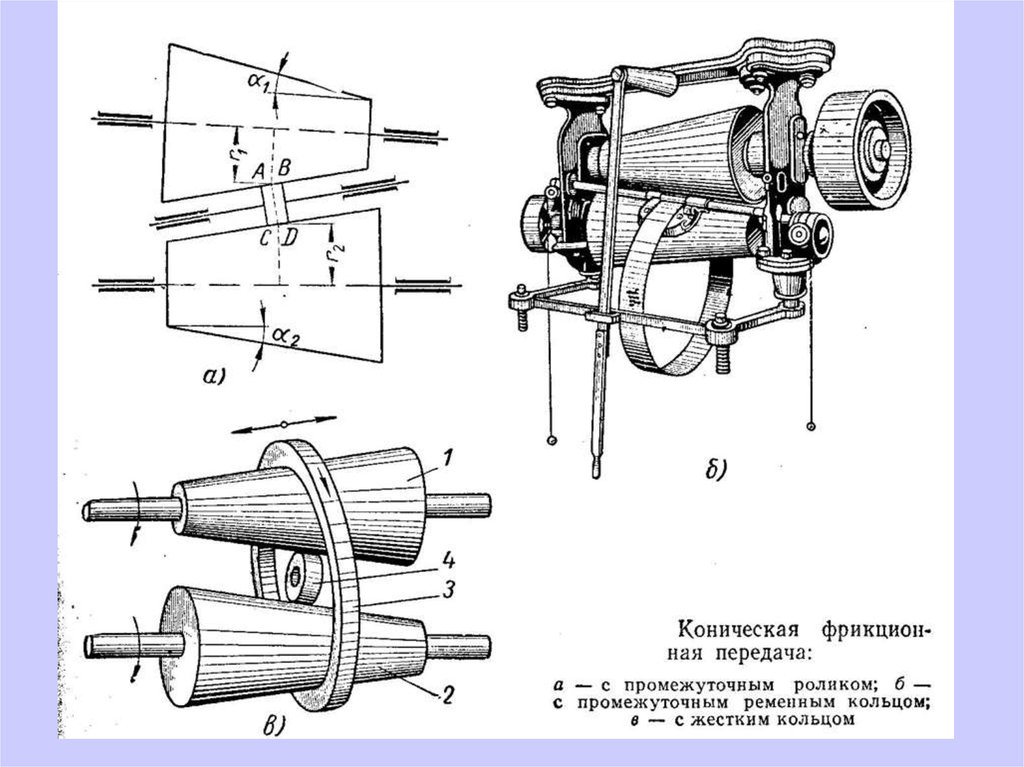
Коническая передачаПо форме рабочей поверхности катковые передачи бывают: цилиндрические;
- бочкообразные;
- конические.
60.
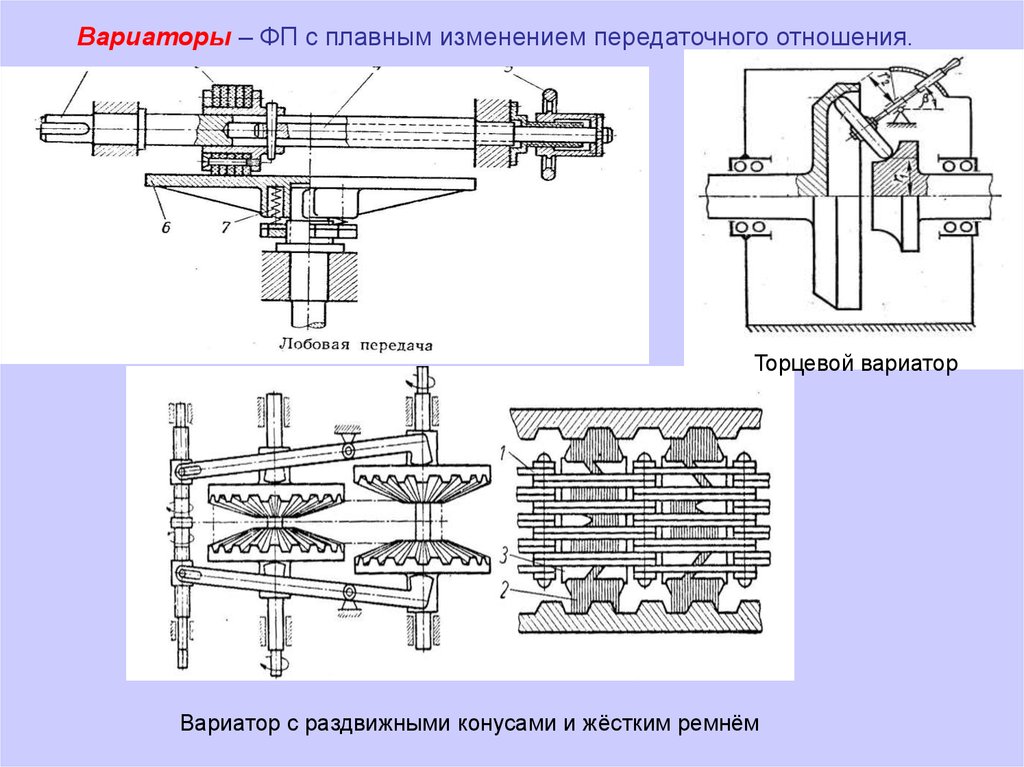
Вариаторы – ФП с плавным изменением передаточного отношения.Торцевой вариатор
Вариатор с раздвижными конусами и жёстким ремнём
61.
62.
5.1.2 Подвижность ФПn 3
p5 2
p4 1
W 3 (n 1) 2 p5 p4 3 (3 1) 2 2 1 1
n 4
p5 4
p4 0
W 3 (n 1) 2 p5 p4 3 (4 1) 2 4 0 1
5.1.3 Кинематический анализ ФП
Если проскальзывание в элементах ФП отсутствует, то из равенства окружной
скорости:
1 R1 2 R2
Передаточное отношение ФП:
1 R2
i12
2 R1
Если известен закон движения ведущего звена, то нет трудностей в
нахождении всех кинематических параметров.
63.
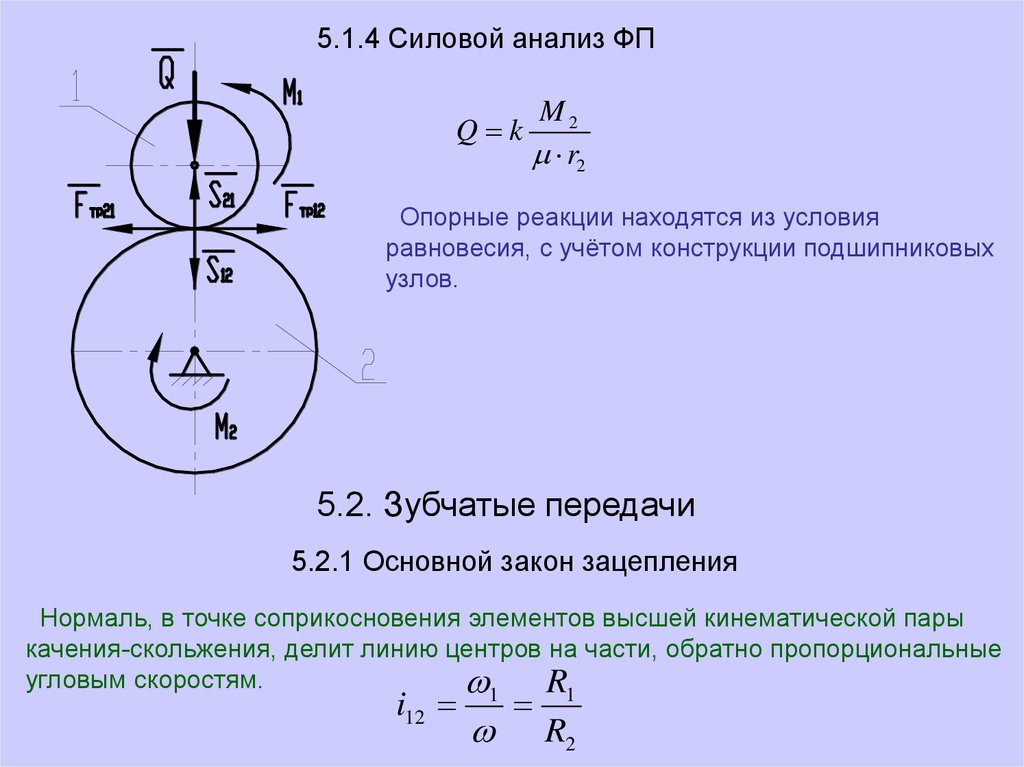
5.1.4 Силовой анализ ФПQ k
M2
r2
Опорные реакции находятся из условия
равновесия, с учётом конструкции подшипниковых
узлов.
5.2. Зубчатые передачи
5.2.1 Основной закон зацепления
Нормаль, в точке соприкосновения элементов высшей кинематической пары
качения-скольжения, делит линию центров на части, обратно пропорциональные
угловым скоростям.
R
i12
1
1
R2
64.
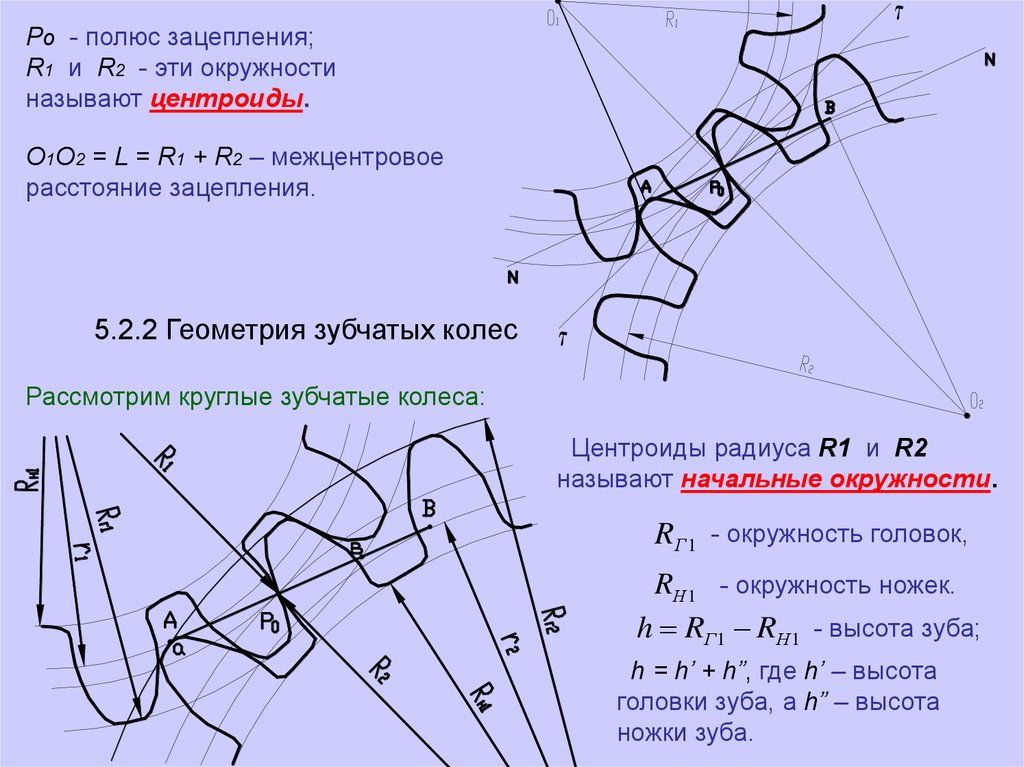
Ро - полюс зацепления;R1 и R2 - эти окружности
называют центроиды.
О1О2 = L = R1 + R2 – межцентровое
расстояние зацепления.
5.2.2 Геометрия зубчатых колес
Рассмотрим круглые зубчатые колеса:
Центроиды радиуса R1 и R2
называют начальные окружности.
R Г 1 - окружность головок,
RН 1 - окружность ножек.
h RГ1 RН1 - высота зуба;
h = h’ + h”, где h’ – высота
головки зуба, а h” – высота
ножки зуба.
65.
h' = RГ1 – R1 ;h” = R1 – RН1.
а' – длина дуги начальной окружности – ширина зуба,
а” – длина дуги начальной окружности – ширина впадины.
tH – длина дуги начальной окружности – шаг зацепления.
z1
m
tH
2 R1 2 R1
tH
m
tH = а' + а”
– число зубьев
- модуль зацепления (вводится, чтобы избавиться от
иррациональности).
Модуль, полученный из расчета, округляется до ближайшего значения по
стандарту (ГОСТ 9563-61):
1 ряд (предпочтительный): 0; 0.05; … 0.5; 0.8; 1.0; 1.25; 1.5; 2.0; 2.5; 3; 4: 5; 8;10;
12; … 100.
2 ряд (добавлены некоторые промежуточные значения): 3.5; 4.5; 7; 9; и т.д.
Окружность зубчатого колеса, для которой модуль получается стандартный,
называется делительной.
Колеса, у которых совпадают диаметры начальной и делительной окружностей,
называются коромысловыми.
66.
Зубья бывают нормальные и сукороченной головкой.
h' = ’m;
зуб
нормальный
’
1
0.8
”
1.25
1.1
h” = ”m;
Угол зацепления (давления):
= 20
укороченный
(ранее было = 14 30’).
5.2.3 Условия профилирования зубьев
При проектировании профилей зубьев приходится учитывать различные
условия (ограничения):
- Кинематические (обеспечить заданную передаточную функцию, простота
построения профиля);
- Динамические (при постоянстве передаваемой мощности, давление на
зубья и опоры колес должны быть постоянны по величине и направлению,
форма зуба должна обеспечивать максимальную прочность, износ зубьев
должен быть минимальным, отсутствие ударов и т.д.);
- Технологические (простота изготовления на современных станках и др.);
- Эксплуатационные (долговечность механизма, бесшумность работы,
легкость монтажа и ремонта и др.)
С учетом этого в машиностроении обычно используются только несколько
кривых для профилирования зубьев. Чаще всего используется эвольвента
круга.
67.
Эвольвента получается путемразматывания нити с окружности.
Эволюта – геометрическое место
точек кривизны эвольвенты.
R - основная окружность в зубчатом
зацеплении (образует эвольвенту).
Свойства эвольвенты:
1) Эвольвентное зацепление обеспечивает постоянство передаточной функции
(передаточного отношения), т.к. общая нормаль в любой точке
соприкосновения профилей всегда проходит через полюс зацепления Р0.
2) Размеры основных и начальных окружностей связаны простой
зависимостью: r1 R1 cos ; r2 R2 cos
3) Передаточное отношение i12 не зависит от угла зацепления , а только от
R
r
радиусов основных окружностей.
i12 1 2 2 2
- радиус кривизны эвольвенты.
R
r
2
1
1
1
4) При изменении расстояния О1О2 (монтаж, сборка) передаточное отношение
не меняется. При этом монтажный угол зацепления 3 - расчетного угла
зацепления.
68.
5.2.4 Параметры эвольвентного зацепления и его профилированиеРассмотрим внешнее эвольвентное
зацепление нормальных колёс.
Из расчётов и конструктивных
соображений обычно бывает
известно:
- i12 – передаточное отношение;
- m – модуль зацепления;
- z1 и z2 - число зубьев колёс;
- А – межосевое (межцентровое)
расстояние (О1О2).
Находим радиусы делительных
окружностей и строим их в масштабе
из точек О1 и О2.
Нормаль N образует угол W = 20 с касательной к делительным окружностям в
точке Р0.
Линией зацепления называется геометрическое место точек зацепления на
неподвижной плоскости.
АВ – теоретическая линия зацепления (предельная длина).
ав - практическая линия зацепления (заключена между окружностями головок).
69.
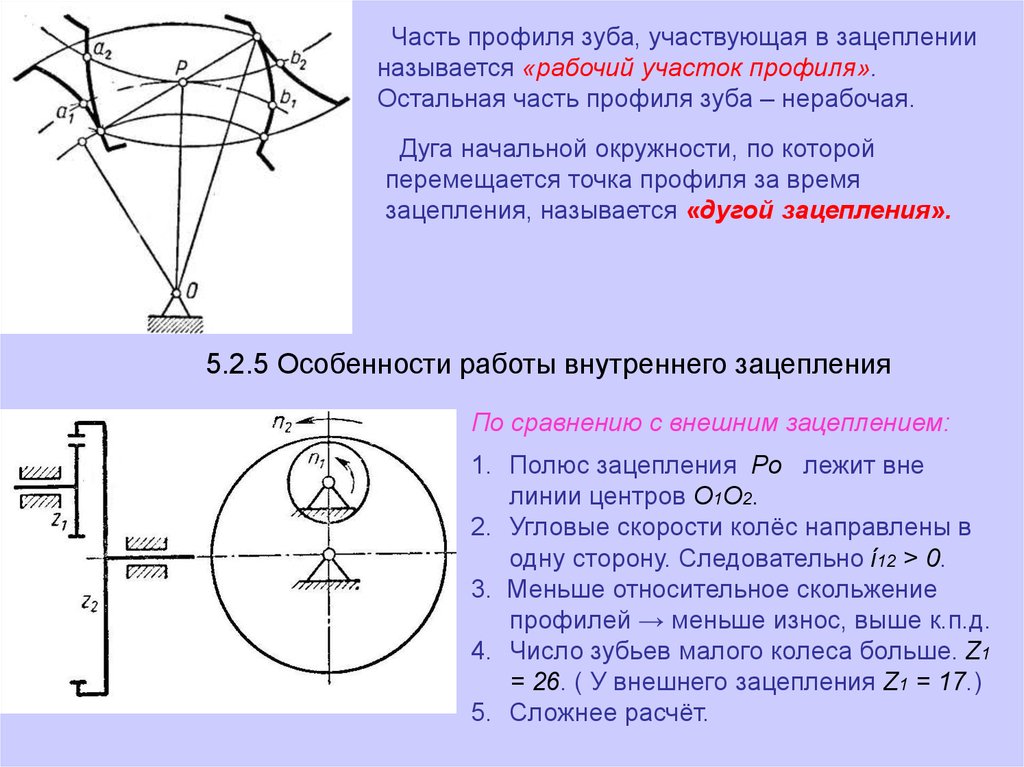
Часть профиля зуба, участвующая в зацепленииназывается «рабочий участок профиля».
Остальная часть профиля зуба – нерабочая.
Дуга начальной окружности, по которой
перемещается точка профиля за время
зацепления, называется «дугой зацепления».
5.2.5 Особенности работы внутреннего зацепления
По сравнению с внешним зацеплением:
1. Полюс зацепления Ро лежит вне
линии центров О1О2.
2. Угловые скорости колёс направлены в
одну сторону. Следовательно ί12 > 0.
3. Меньше относительное скольжение
профилей → меньше износ, выше к.п.д.
4. Число зубьев малого колеса больше. Z1
= 26. ( У внешнего зацепления Z1 = 17.)
5. Сложнее расчёт.
70.
6. Коэффициент перекрытия ε – выше.7. Нельзя использовать инструментальную рейку для изготовления колеса 2.
8. Нежелательный эффект – наложение (интерференция) зубьев.
5.2.6 Другие виды зацеплений
А) Циклоидальное зацепление
Головка зуба профилируется по эпициклоиде, ножка – по гипоциклоиде.
Построение эпициклоиды
Построение гипоциклоиды
71.
Достоинства циклоидального зацепления по сравнению с эвольветным:1. Скорость скольжения профилей и удельное скольжение – ниже (выше к.п.д.,
меньше износ).
2. Удельное давление в контакте – ниже.
3. Невозможно подрезание ножки зуба → Z1 = 9 или даже 7.
Недостатки циклоидального зацепления по сравнению с эвольветным:
1. Более сложный инструмент для нарезания зубьев – в инструментальной
рейке не прямые, а циклоиды.
2. Высокая чувствительность к ошибкам при изготовлении и при сборке.
3. Высокая стоимость изготовления.
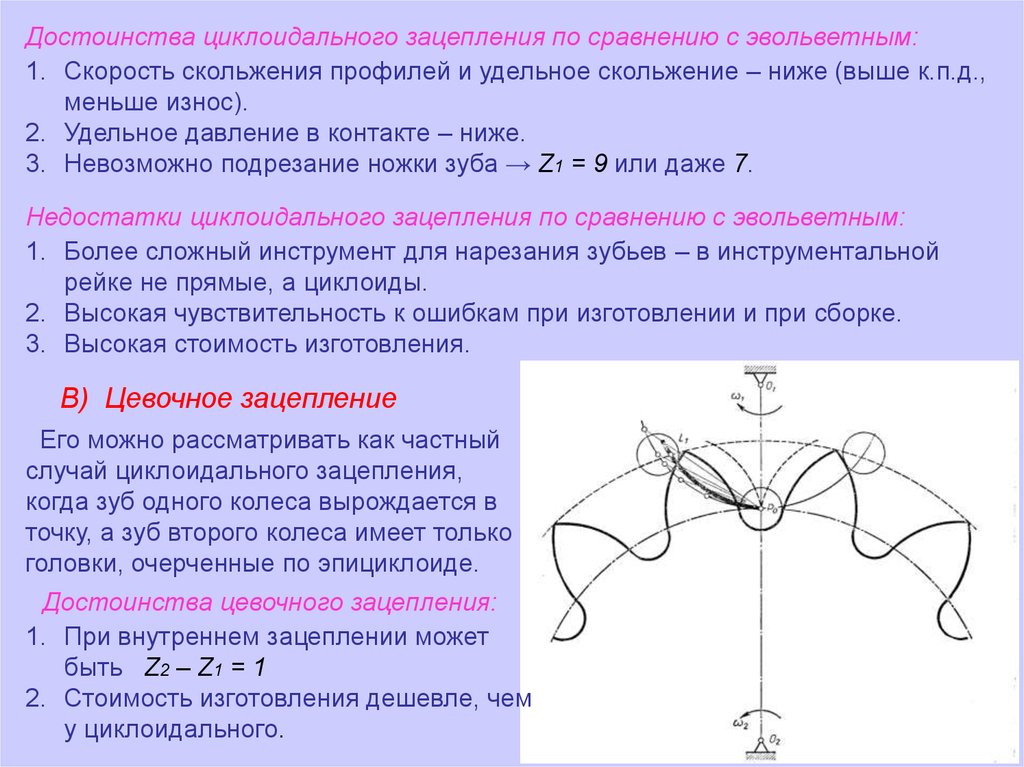
В) Цевочное зацепление
Его можно рассматривать как частный
случай циклоидального зацепления,
когда зуб одного колеса вырождается в
точку, а зуб второго колеса имеет только
головки, очерченные по эпициклоиде.
Достоинства цевочного зацепления:
1. При внутреннем зацеплении может
быть Z2 – Z1 = 1
2. Стоимость изготовления дешевле, чем
у циклоидального.
72.
Недостатки цевочного зацепления:1. Линия зацепления не прямая, а кусок кардиоиды.
2. Сложнее расчёт.
3. Больше работа сил трения → меньше к.п.д.
С) Зацепление Новикова
Можно рассматривать как частный случай цевочного зацепления, когда
головки зуба одного колеса – неподвижные цевки, выступающие над начальной
окружностью, а зуб второго колеса имеет только ножки, очерченные по дуге
окружности. Зубья – косые.
αs = (20 – 30)
73.
Достоинства зацепления:1. Возможность передавать большие давления в контакте.
2. Меньше скольжение и выше к.п.д.
Недостатки зацепления:
1. Меньше коэффициент перекрытия, чем в косозубом эвольвентном
зацеплении.
2. Очень сложный расчёт.
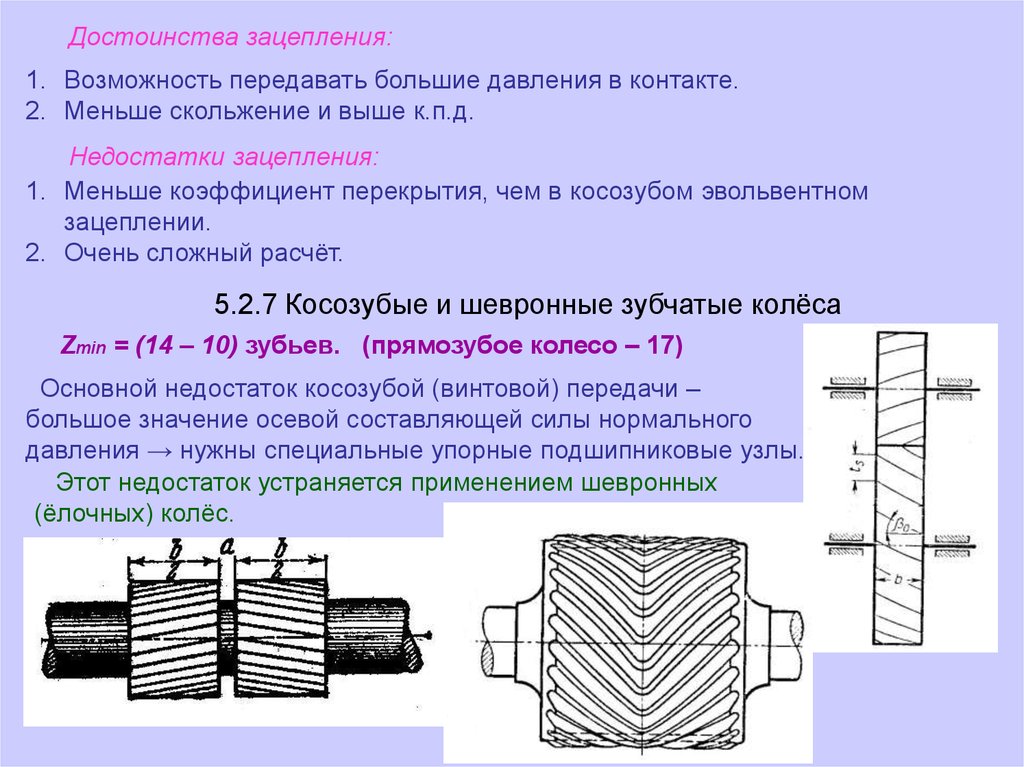
5.2.7 Косозубые и шевронные зубчатые колёса
Zmin = (14 – 10) зубьев. (прямозубое колесо – 17)
Основной недостаток косозубой (винтовой) передачи –
большое значение осевой составляющей силы нормального
давления → нужны специальные упорные подшипниковые узлы.
Этот недостаток устраняется применением шевронных
(ёлочных) колёс.
74.
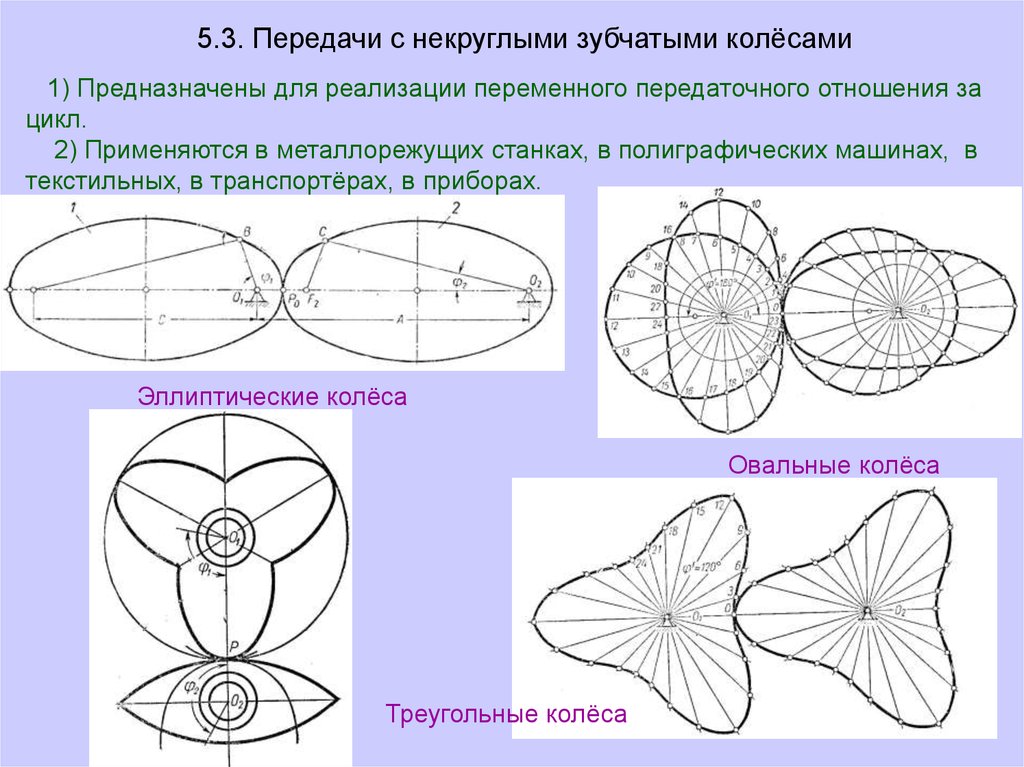
5.3. Передачи с некруглыми зубчатыми колёсами1) Предназначены для реализации переменного передаточного отношения за
цикл.
2) Применяются в металлорежущих станках, в полиграфических машинах, в
текстильных, в транспортёрах, в приборах.
Эллиптические колёса
Овальные колёса
Треугольные колёса
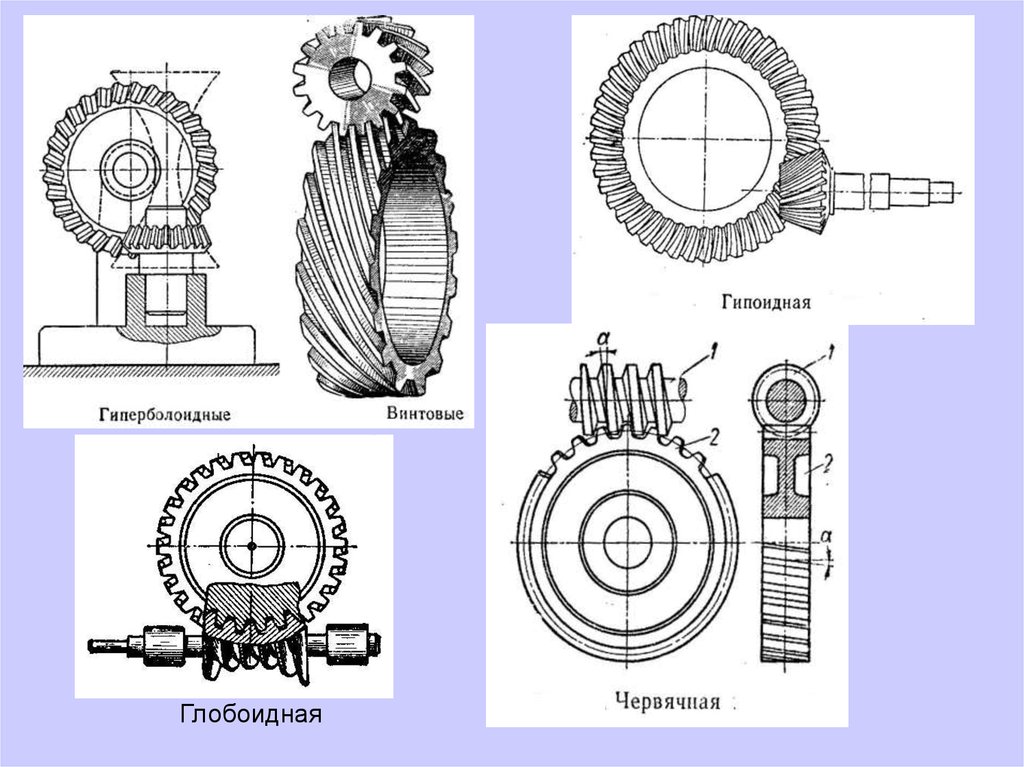
75. Пространственные зубчатые передачи.
1) со скрещивающимися осями:• гиперболоидные;
• винтовые;
• гипоидные;
• червячные;
• глобоидные (тороидные);
• спироидные.
2) с пересекающимися осями:
• конические;
• октоидальные.
76.
Глобоидная77.
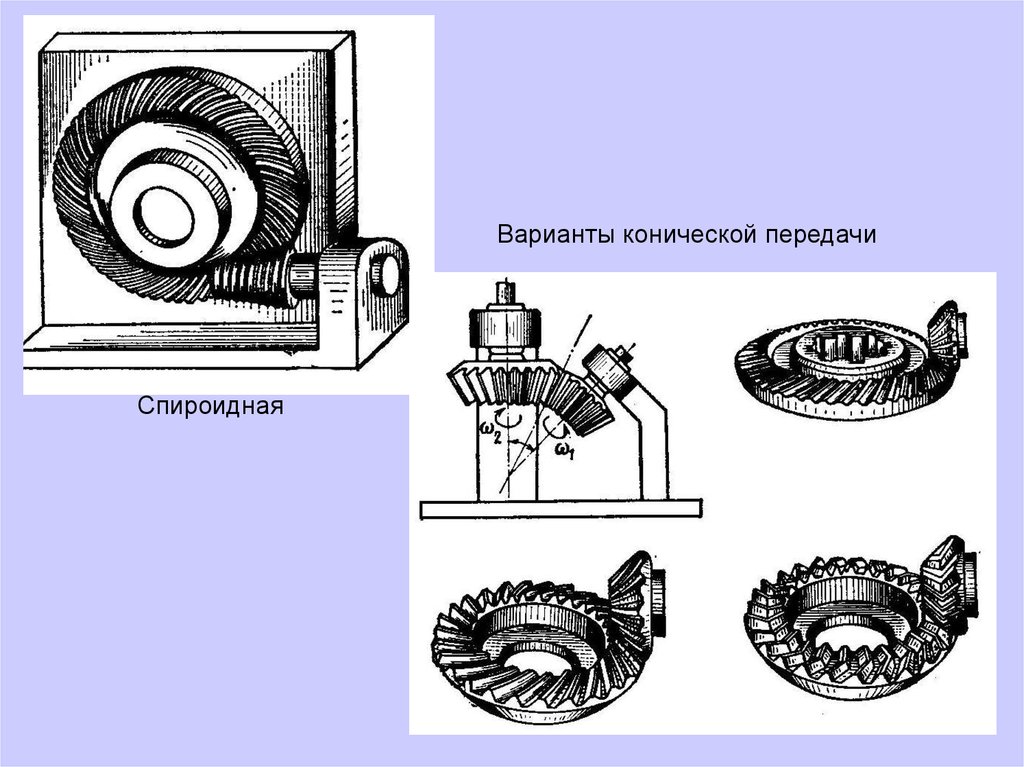
Варианты конической передачиСпироидная
78.
6. Многозвенные зубчатые механизмыЗадача 1. По заданным числам зубьев, найти передаточное отношение.
- вполне определённа.
Задача 2. По заданному i найти схему редуктора и числа зубьев колёс.
- неопределённа, имеет бесчисленное множество решений.
6.1 Редукторы с неподвижными осями колёс
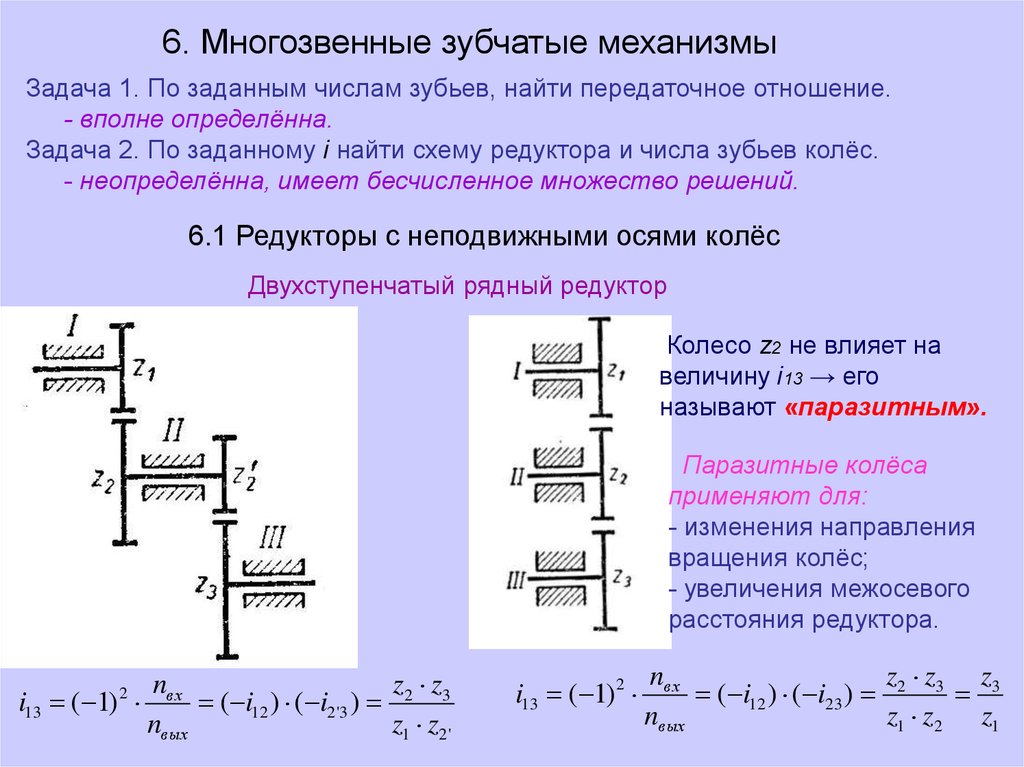
Двухступенчатый рядный редуктор
Колесо z2 не влияет на
величину i13 → его
называют «паразитным».
Паразитные колёса
применяют для:
- изменения направления
вращения колёс;
- увеличения межосевого
расстояния редуктора.
n
z z
i13 ( 1) вх ( i12 ) ( i2'3 ) 2 3
nвых
z1 z2'
2
i13 ( 1) 2
nв х
z z
z
( i12 ) ( i23 ) 2 3 3
nв ых
z1 z2 z1
79.
Редуктор, в котором можно изменятьпередаточное отношение дискретно, меняя
комбинации различных зубчатых колёс, называют
«коробка скоростей».
6.2 Редукторы с подвижными осями колёс
- называют «эпициклические».
Простейшие схемы эпициклических (планетарных) редукторов:
80.
Рассмотрим схему, применяемую чаще всего.1 – солнечное (центральное) колесо; 2 – сателлит; 3
– коронное колесо; Н – водило (поводок).
W 3 (n 1) 2 p5 p4 3 (4 1) 2 3 2 1 1
Если закрепить относительно стойки водило Н и
освободить колесо 3, то получим рядную передачу с
неподвижными осями и паразитным колесом 2.
Если освободить колесо 3, то получим эпициклическую
передачу более общего вида с двумя степенями свободы
(дифференциальная передача).
W 3 (n 1) 2 p5 p4
3 (5 1) 2 4 2 1 2
Такая передача может обеспечить:
- работу 2 исполнительных
механизмов от 1 двигателя;
- работу 1 исполнительного
механизма от 2 двигателей.
81.
Достоинства эпициклических передач:- высокое передаточное отношение;
- лёгкость и компактность;
- возможность работы 2-х двигателей на 1 выходной вал и наоборот.
Найдём передаточное отношение этой ступени редуктора
(используем метод обращения).
звено
Угловая скорость
Если остановить Н
Z1
ω1
ω1 - ωH = ω1*
Z2-Z2’
ω2
ω2 - ωH = ω2*
Z3
ω3
ω3 - ωH = ω3*
H
ωH
0
1* 1 H
i13 *
;
3 3 H
Z Z
i13 2 3 ;
Z1 Z 2'
2* 2 H
i2'3 *
.
3 3 H
i2 '3
Z3
Z 2'
82.
7. Уравновешивание механизмов и балансировка роторов.7.1. Вибрации и колебания в машинах и механизмах.
При движении механической системы под действием внешних сил в ней могут
возникать механические колебания или вибрации. Причинами возникновения
вибраций могут быть периодические изменения сил (силовое возмущение),
перемещений (кинематическое возмущение) или инерционных характеристик
(параметрическое возмущение).
Вибрацией ( от лат. vibratio - колебание ) называют механические колебания в
машинах или механизмах. Колебание - движение или изменение состояния,
обладающие той или иной степенью повторяемости или периодичностью.
Если источник возникновения вибраций определяется внутренними
свойствами машины или механизма, то говорят о его виброактивности. Чтобы
вибрации механизма не распространялись на окружающие его системы или
чтобы защитить механизм от вибраций, воздействующих на него со стороны
внешних систем, применяются различные методы виброзащиты.
83.
Внутренняя виброактивность – колебания возникающие внутри механизмаили машины, которые происходят по его подвижностям или обобщенным
координатам. При внешней виброактивности изменение положения механизма
приводит к изменению реакций в опорах (т.е. связях механизма с окружающей
средой) и непосредственному вибрационному воздействию на связанные с ним
системы. Одна и основных причин внешней виброактивности неуравновешенность его звеньев и механизма в целом.
Основными динамическими составляющими при работе любого механизма
являются силы инерции, которые, как правило, переменны по величине и
направлению. Это характерно и для случаев, когда входное звено вращается с
постоянной угловой скоростью 1 const
Все силы и моменты сил инерции можно привести к главному вектору и
моменту относительно выбранной точки:
F и F ui
M и M ui Fui h
Fui
Полностью уравновешенным считается механизм, в котором сила давления
стойки на фундамент остаётся постоянной при движении звеньев
Fu 0
M u 0
Для выполнения условия Fu 0 необходимо, чтобы аs 0 .
аs ускорение центра масс системы.
84.
Это равносильно требованию постоянства положения центра масс механизмаотносительно стойки. Такое уравновешивание называется статическим или
уравновешиванием первого рода.
Выполнение условия M u 0 решается при моментном (динамическом)
уравновешивании, которое называется уравновешиванием второго рода.
7.2. Уравновешивание вращающихся масс (роторов)
Ротором в теории балансировки называется любое вращающееся тело.
Различают статическое уравновешивание (статическая балансировка)
вращающихся роторов и динамическое.
Статическая балансировка достигается тем, что центр тяжести вращающейся
детали переводят в неподвижную точку. Такое уравновешивание применяется
для плоских деталей, длина которых мала по сравнению с диаметром.
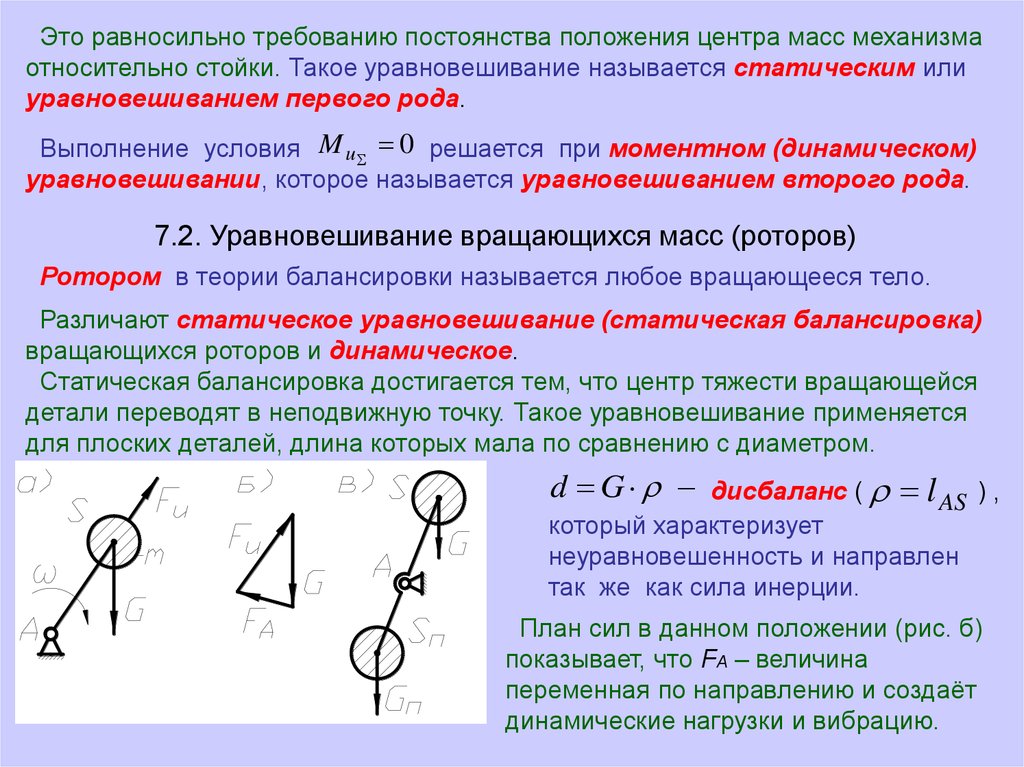
d G
дисбаланс ( l AS ) ,
который характеризует
неуравновешенность и направлен
так же как сила инерции.
План сил в данном положении (рис. б)
показывает, что FA – величина
переменная по направлению и создаёт
динамические нагрузки и вибрацию.
85.
Необходимо уравновесить дисбаланс установкой массы противовеса спротивоположной стороны (рис. в). Тогда дисбалансы будут уравновешены.
Статическая балансировка осуществляется на
балансировочных призмах (или ножах).
Существуют и более сложные приборы для
статического уравновешивания, у которых масса
необходимого противовеса и место, где он должен
устанавливаться, определяются по показанию
специального прибора.
Динамически балансируют роторы, размеры которых вдоль оси вращения
значительны (например, валы, роторы газотурбинных двигателей и т.д.)
Распределение масс ротора,
устраняющее давление от его сил
инерции на стойку, называется полным
уравновешиванием ротора.
Выполняется на специальных
установках, в которых ротор вращается
(см. лабораторный практикум).















































 Механика
Механика








