Достоверность различий между двумя независимыми результатами. Параметрические критерии Стьюдента и Фишера

1.

Практические занятия № 20-21.
Определение достоверности различий между двумя
независимыми результатами. Параметрические критерии
Стьюдента и Фишера
Критерий Фишера
Задание 1. Рассмотрим результаты контрольной xi и экспериментальной yi
групп спортсменов по скорости бега ( м/с ) (столбцы xi , ni , yi , ni , значения выделены
красным цветом) (таблица 1). Достоверно ли различия в скорости бега у этих групп для
характеристик рассеивания?
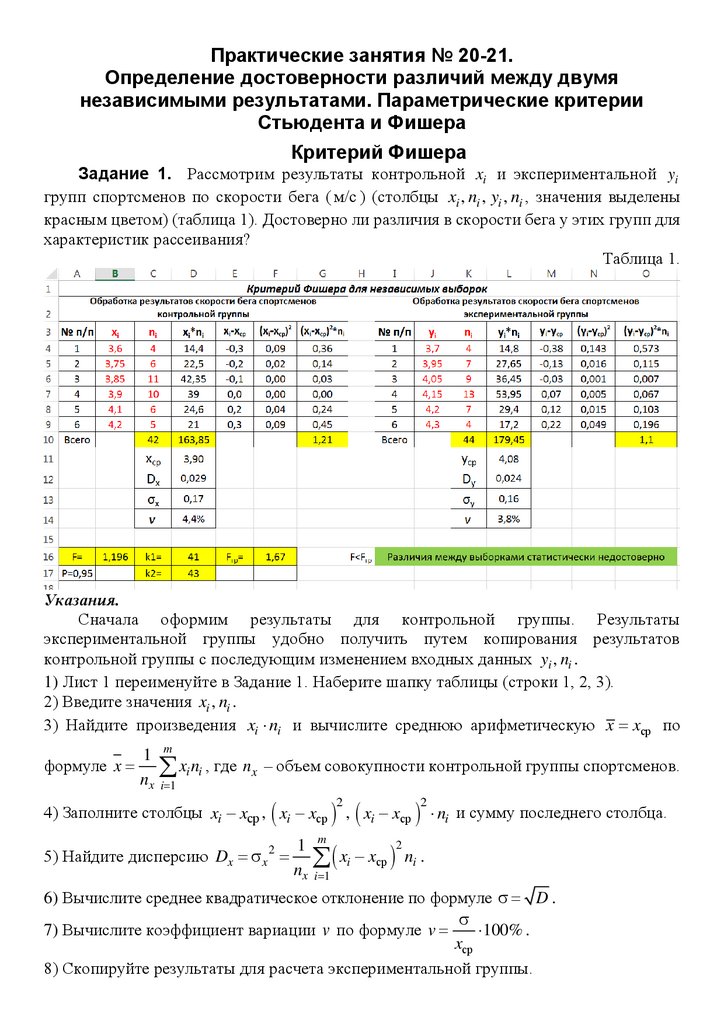
Таблица 1.
Указания.
Сначала оформим результаты для контрольной группы. Результаты
экспериментальной группы удобно получить путем копирования результатов
контрольной группы с последующим изменением входных данных yi , ni .
1) Лист 1 переименуйте в Задание 1. Наберите шапку таблицы (строки 1, 2, 3).
2) Введите значения xi , ni .
3) Найдите произведения xi ni и вычислите среднюю арифметическую x xср по
1 m
формуле x xi ni , где nx – объем совокупности контрольной группы спортсменов.
nx i 1
4) Заполните столбцы xi xср , xi xср
, xi xср ni и сумму последнего столбца.
2
2
2
1 m
5) Найдите дисперсию Dx x xi xср ni .
nx i 1
2
6) Вычислите среднее квадратическое отклонение по формуле D .
100% .
7) Вычислите коэффициент вариации v по формуле v
xср
8) Скопируйте результаты для расчета экспериментальной группы.

2.

9) Замените заголовок, xi , ni на yi , ni ; формулу для xi xср на yi yср (при копировании
абсолютную ссылку на xср надо вручную заменить на ссылку на yср .
10) В ячейке В16 определите значение критерия Фишера по формуле: F
D1
,
D2
где D1 , D2 – дисперсии сравниваемых выборок.
Замечание. Условиями критерия Фишера предусмотрено, что в числителе
формулы вычисления критерия Фишера находится большая дисперсия, т.е. число
F всегда больше единицы.
В нашем случае D1 Dx , D2 Dy , т.к. Dx Dy . В дальнейших расчетах индекс 1 будет
соответствовать выборке x , а индекс 2 будет соответствовать выборке y .
11) Задайте надежность счета P 0,95 и определите числа степеней свободы для обоих
выборок: k1 n1 1 nx 1 42 1 41 ; k2 n2 1 ny 1 44 1 43 .
С помощью статистической функции F.ОБР.ПХ находим граничное значение
критерия Fгр 1,67 . Аргументами функции F.ОБР.ПХ являются: вероятность (равно
0,05), степень свободы 1 (равно k1 41 ) и степень свободы 2 (равно k2 43 ).
Статистический вывод. Поскольку F Fгр (1,196 1,67 ), то различие между
выборками статистически недостоверно.
Педагогический вывод. Различия в скорости бега у этих групп для характеристик
рассеивания недостоверно, несущественно. По характеристикам рассеивания эти
группы не следует рассматривать как различные.
Задание 2. Расчет различия между двумя несвязанными выборками с
помощью критерия Фишера методами Microsoft Excel
Аналогичное сравнение двух несвязанных выборок можно провести в Microsoft
Excel с помощью статистической функции F.ТЕСТ или процедуры Двухвыборочный Fтест для дисперсий из Анализ данных.
Указания.
1) Лист 2 переименуйте в Задание 2. Аналогично показанному в таблице 2 наберите все
значения xi и yi в ячейках А3: А44, В3: В46 (на рисунке не все данные – только
начало).
2) Для дополнительной проверки сосчитайте количество значений в столбцах xi и yi в
ячейках А45 и В47 (с помощью статистической функции СЧЕТ).
3) В ячейке A48 напишите комментарий F.ТЕСТ. В ячейке В48 с помощью функции
F.ТЕСТ из категории Статистические найдем вероятность соответствующую критерию
Фишера:
массив 1: А3:А44;
массив 2: В3:В46;
Получим значение F 0,56 .
Если F 0,05 , то выборки относятся к двум разным совокупностям и различие
между выборками статистически достоверно.
Если F 0,05 , то выборки относятся к одной совокупности и различие между
выборками статистически недостоверно.
Вывод. Мы получили F 0,05 ( 0,56 0,05 ) и выборки относятся к одной

3.

совокупности, различие между выборками статистически недостоверно.
Таблица 2.
Аналогичный вывод можно сделать с помощью процедуры Двухвыборочный Fтест для дисперсий.
Вызываем процедуру Двухвыборочный F-тест для дисперсий. Для этого, указав
курсором мыши на пункт меню Данные, выберите команду Анализ данных. Затем в
появившемся списке Инструменты анализа выберите строку Двухвыборочный Fтест для дисперсий.
В появившемся диалоговом окне в рабочем поле Интервал переменной 1 укажите
входной диапазон значений xi – А3:А44, Интервал переменной 2 укажите входной
диапазон значений yi – В3:В46. Переключателем активизируйте Выходной интервал
и укажите выходной диапазон — ячейку D2. Проверьте, что в поле Альфа указано
0,05. Затем нажмите кнопку ОК.
Получаем P(F<=t) одностороннее значение (примерно) 0,28.
Умножив его на 2, получим то же значение F 0,56 .
Задание 3. Расчет различия между двумя несвязанными выборками с
помощью критерия Фишера методами StatPlus
Аналогичное сравнение двух несвязанных выборок можно провести в Statplus6 с
помощью F теста для дисперсий из основной статистики.
Рассчитаем достоверность различий данных Задания 1. Для этого воспользуемся
столбцами данных из листа Задание 2.
1) Находясь на листе Задание 2 выбираем STATFI – Основная статистика – F-тест
для дисперсий.
2) Вести диапазон ячеек для переменной 1 и переменной 2. Лучше выделить вместе
с метками xi, yi (находящимся в ячейках А2 и В2). Тогда должна стоять галочка
напротив Метки в первой строке (рис.1).

4.

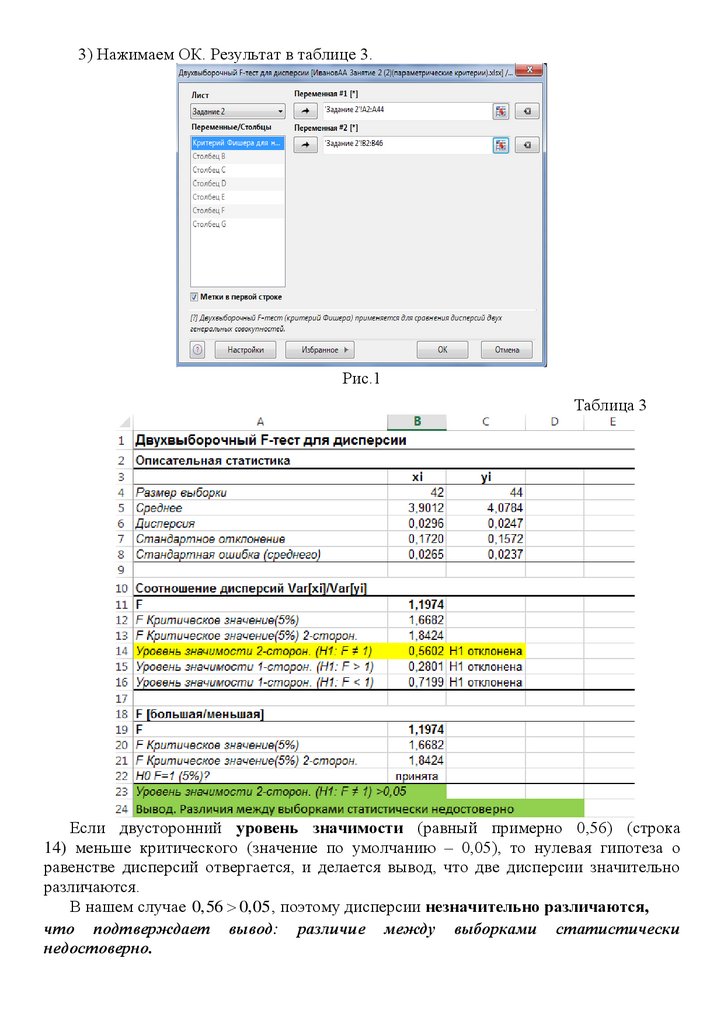
3) Нажимаем ОК. Результат в таблице 3.
Рис.1
Таблица 3
Если двусторонний уровень значимости (равный примерно 0,56) (строка
14) меньше критического (значение по умолчанию – 0,05), то нулевая гипотеза о
равенстве дисперсий отвергается, и делается вывод, что две дисперсии значительно
различаются.
В нашем случае 0,56 0,05 , поэтому дисперсии незначительно различаются,
что подтверждает вывод: различие между выборками статистически
недостоверно.

5.

Критерий Стьюдента
Задание 4. Рассмотрим результаты контрольной xi и экспериментальной yi
групп спортсменов по скорости бега ( м/с ) (столбцы xi , ni , yi , ni , значения выделены
красным цветом) (таблица 4). Достоверно ли различия в скорости бега у этих групп при
сравнении абсолютных показателей выборок (средних значений)?
Указания. 1) Поскольку исходные данные те же, что и в заданиях 1 и 2, то скопируем
лист после листа Задание 2. Переименуем его в Задание 3. Заменим в заголовке
Критерий Фишера на Критерий Стьюдента.
Таблица 4.
x
2) Найти ошибки репрезентативности по формулам mx
nx
, my
y
ny
.
3) Найдите число степеней свободы k nx ny 2 .
4) Найдите значение критерия Стьюдента t
xср yср
mx2 m2y
.
5) С помощью статистической функции СТЬДЕНТ.ОБР.2Х найдите величину
граничного значения критерия ( tгр ). Аргументами функции СТЬДЕНТ.ОБР.2Х
являются: вероятность (равна уровню значимости 0,05) и степени свободы (равно k )
6) Сравните t и tгр . Сделайте статистический и педагогический выводы.
Статистический вывод. Поскольку t tгр , т.е. 5,04 2,00 , то различие между
выборками статистически достоверно.
Педагогический вывод. Различия в средней скорости бега у этих групп по
достоверно, существенно. Скорость бега спортсменов экспериментальной группы
достоверно выше, чем в контрольной группе 4,08 3,90 . Эксперимент удачный.
Задание 5. Расчет различия между выборками с помощью критерия
Стьюдента методами Microsoft Excel

6.

Аналогичное сравнение двух выборок можно провести в Microsoft Excel с
помощью статистической функции СТЬЮДЕНТ.ТЕСТ или процедурами
двухвыборочный t-тест с одинаковыми дисперсиями, двухвыборочный t-тест с
различными дисперсиями из пакета Анализ данных.
Указания.
1) Скопируйте Лист 2 после листа Задание 4 и переименуйте его в Задание 5 (таблица 5).
2) В ячейке А48 замените F.ТЕСТ на СТЬЮДЕНТ.ТЕСТ. В ячейке В48 с помощью
функции СТЬЮДЕНТ.ТЕСТ из категории Статистические найдем вероятность
соответствующую t-тесту Стьюдента, задав:
массив 1: А3:А44;
массив 2: В3:В46;
хвосты: 2;
тип: 2.
Тип 2 соответствует случаю независимых выборок с равными дисперсиями.
Равенство дисперсий было проверено задании 1. Поскольку критерий Фишера
показал, что различие дисперсий статистически недостоверно, то это
соответствует типу 2 для СТЬЮДЕНТ.ТЕСТ.
Получим значение pкрит.=3,188Е-06 (что соответствует 3,188 10 6 ).
Вывод. Если pкрит. 0,05 , то выборки относятся к двум разным совокупностям и
различие между выборками статистически достоверно.
Если pкрит. 0,05 , то выборки относятся к одной совокупности и различие между
выборками статистически недостоверно.
Таблица 5.
Мы получили pкрит. 0,05 ( 3,188 10 6 0,05 ) и выборки относятся к двум
разным совокупностям, различие между выборками статистически достоверно.

7.

Аналогичный вывод можно сделать с помощью процедуры Двухвыборочный tтест с одинаковыми дисперсиями.
Указания.
1) Вызываем процедуру Двухвыборочный t-тест с одинаковыми дисперсиями. Для
этого, указав курсором мыши на пункт меню Данные, выберите команду Анализ данных.
Затем в появившемся списке Инструменты анализа выберите строку Двухвыборочный
t-тест с одинаковыми дисперсиями.
2) В появившемся диалоговом окне в рабочем поле Интервал переменной 1 укажите
входной диапазон значений xi – А3:А44, Интервал переменной 2 укажите входной
диапазон значений yi – В3:В46. Переключателем активизируйте Выходной интервал и
укажите выходной диапазон — ячейку D2. Проверьте, что в поле Альфа указано 0,05.
Затем нажмите кнопку ОК.
3) Получаем P(T<=t) двухстороннее то же значение 3,188E 06 3,188 10 6
Задание 6. Расчет различия между двумя несвязанными выборками с
помощью критерия Стьюдента методами StatPlus
Аналогичное сравнение двух несвязанных выборок можно провести в Statplus6 с
помощью процедуры Сравнение средних (t-тест) из основной статистики.
Рассчитаем достоверность различий данных Задания 4. Для этого воспользуемся
столбцами данных из листа Задание 5 (или Задания 2).
1) Находясь на листе Задание 5 выбираем STATFI – Основная статистика –
Сравнение средних (t-тест).
2) Аналогично заданию 3 вести диапазон ячеек для переменной 1 и переменной 2.
Лучше выделить вместе с метками xi, yi (находящимся в ячейках А2 и В2). Тогда должна
стоять галочка напротив Метки в первой строке.
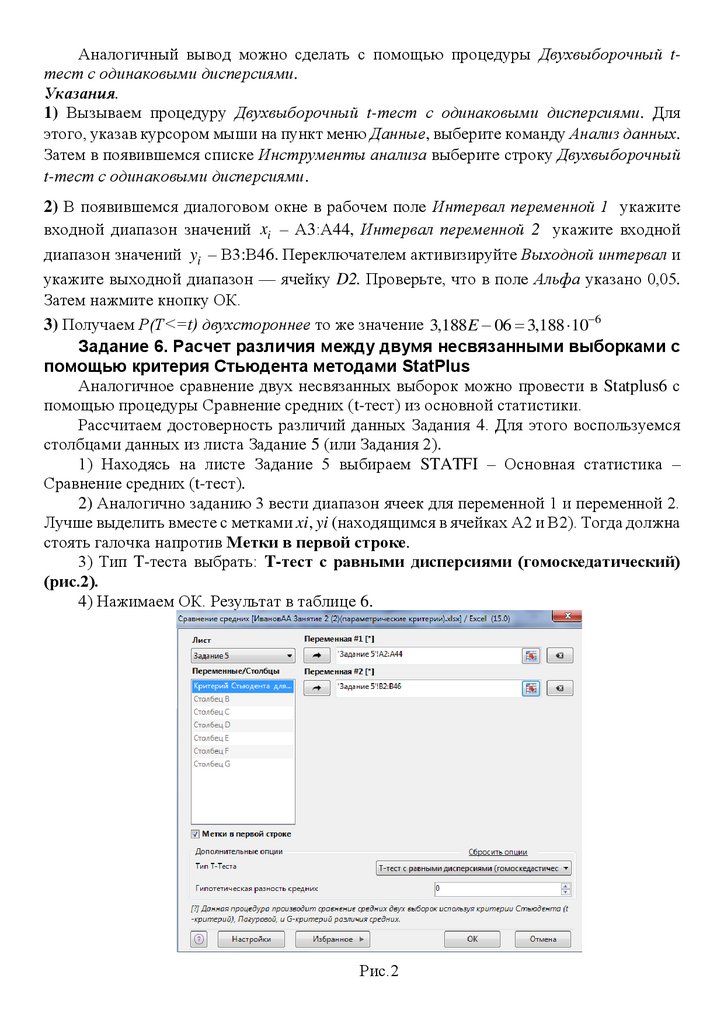
3) Тип T-теста выбрать: T-тест с равными дисперсиями (гомоскедатический)
(рис.2).
4) Нажимаем ОК. Результат в таблице 6.
Рис.2

8.

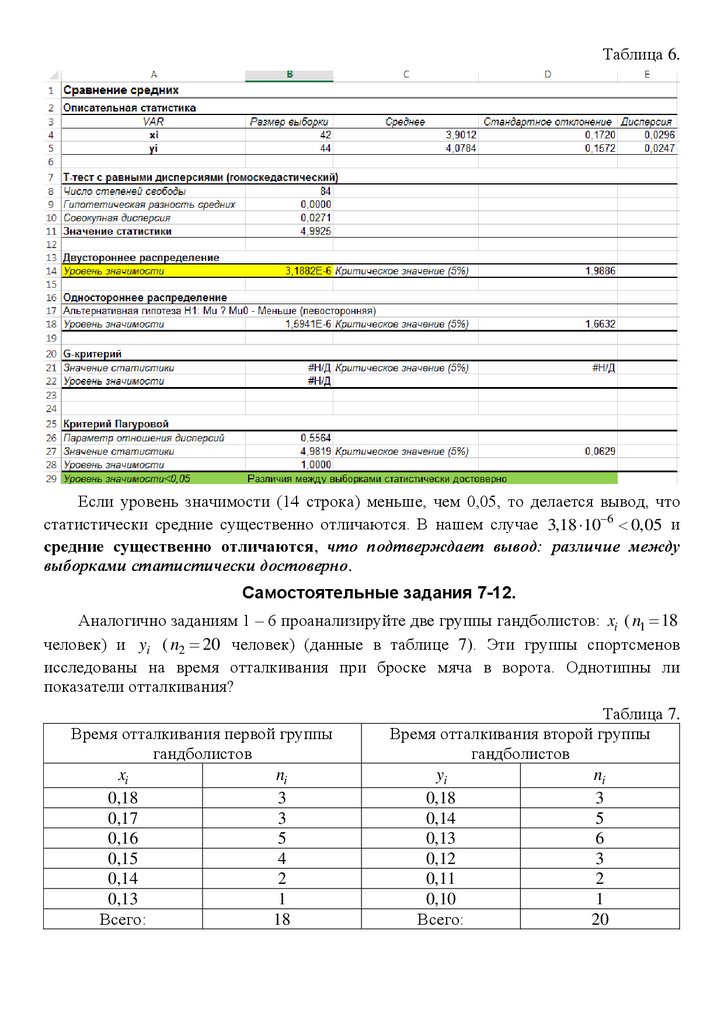
Таблица 6.
Если уровень значимости (14 строка) меньше, чем 0,05, то делается вывод, что
статистически средние существенно отличаются. В нашем случае 3,18 10 6 0,05 и
средние существенно отличаются, что подтверждает вывод: различие между
выборками статистически достоверно.
Самостоятельные задания 7-12.
Аналогично заданиям 1 – 6 проанализируйте две группы гандболистов: xi ( n1 18
человек) и yi ( n2 20 человек) (данные в таблице 7). Эти группы спортсменов
исследованы на время отталкивания при броске мяча в ворота. Однотипны ли
показатели отталкивания?
Время отталкивания первой группы
гандболистов
xi
ni
0,18
3
0,17
3
0,16
5
0,15
4
0,14
2
0,13
1
Всего:
18
Таблица 7.
Время отталкивания второй группы
гандболистов
ni
yi
0,18
3
0,14
5
0,13
6
0,12
3
0,11
2
0,10
1
Всего:
20