Wprowadzenie do Trygonometrii. Podstawowe Pojęcia i Zastosowania

1.

Wprowadzenie do Trygonometrii
Podstawowe Pojęcia i Zastosowania
Autorem tej prezentacji jest Oleksandr Stretovych

2.

Co to jest trygonometria?
Trygonometria - to dział matematyki, który zajmuje się zależnościami między długościami boków,
a miarami kątów wewnętrznych w trójkątach. Rozszerzeniem podstawowej trygonometrii są tzw.
funkcje trygonometryczne, które często pojawiają się w analizie matematycznej.W pewnym
uproszczeniu można powiedzieć, że:
Istnieją 4 funkcje trygonometryczne: sinus, cosinus, tangens i cotangens.
Funkcje te działają na kątach.
Definiuje się je w trójkącie prostokątnym jako stosunki odpowiednich boków.
Trygonometria ma bardzo szerokie zastosowanie w wielu dziedzinach życia, w których niezbędne
jest mierzenie i obliczanie rzeczywistych wielkości.Mając do dyspozycji jedynie zwykłą miarkę i
kątomierz możemy obliczyć wysokość dowolnej góry, lub szerokość rzeki.
Trygonometria jest podstawą do wykonywania wszelkich pomiarów na powierzchni ziemi,
umożliwia działanie urządzeń nawigacyjnych (GPS), a także pozwala na prowadzenie badań
astronomicznych.Dzięki tzw. szeregom Fouriera (są to nieskończone sumy funkcji
trygonometrycznych - zaawansowane narzędzie analizy matematycznej) możliwe jest
przetwarzanie wielu sygnałów, m.in. kompresja muzyki w formacie mp3 oraz grafiki w formacie
jpg.

3.

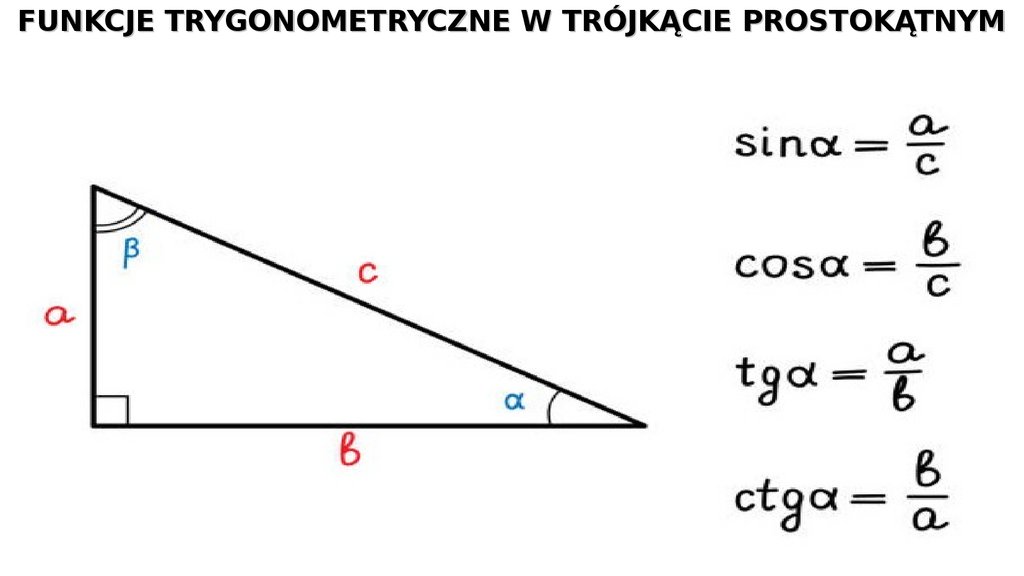
FUNKCJE TRYGONOMETRYCZNE W TRÓJKĄCIE
PROSTOKĄTNYM
Funkcje trygonometryczne dla kątów ostrych można zdefiniować jako stosunki długości
odpowiednich dwóch boków trójkąta prostokątnego dla danej miary kąta wewnętrznego.
sinus – oznaczany sin – stosunek przyprostokątnej przeciwległej do kąta ostrego i
przeciwprostokątnej
cosinus – oznaczany cos – stosunek przyprostokątnej przyległej do kąta ostrego i
przeciwprostokątnej
tangens – oznaczany tg– stosunek przyprostokątnej przeciwległej do kąta ostrego i
przyprostokątnej przyległej do kąta ostrego
cotangens– oznaczany ctg – stosunek przyprostokątnej przyległej do kąta ostrego i
przyprostokątnej przeciwległej do kąta ostrego

4.

MIARA KĄTA NA PODSTAWIE WARTOŚCI FUNKCJI
TRYGONOMETRYCZNYCH - liczenie za pomocą kalkulatora
WINDOWS XP
PRZYKŁAD:
Do jakiego kąta α sinα=0,32 ?
Uruchamiamy kalkulator
Start> Wszystkie programy> Akcesoria> Kalkulator
w menu: Widok> Naukowy
Wpisujemy 0,32 zaznaczamy „Inv” i naciskamy „sin”
○
α≈18,66

5.

FUNKCJE TRYGONOMETRYCZNE W TRÓJKĄCIE PROSTOKĄTNYM

6.

Podstawowe tozsamosci
trygonometryczne
Moim zdaniem latwiej nauczycz z
tych wzorow

7.

Podstawowe Tożsamości Trygonometryczne
Funkcje trygonometryczne w trójkącie prostokątnym:
Prawo sinusów: Dla dowolnego trójkąta, stosunek długości boków do sinusów przeciwległych kątów jest stały
a
sin(a)
=
b
sin(b
)
=
c
sin(y)
Prawo cosinusów: Dla dowolnego trójkąta, kwadrat długości boku jest równy sumie kwadratów pozostałych
dwóch boków minus podwojony iloczyn tych boków i cosinusa kąta między nimi
c2=a2+b2−2ab cos(γ)

8.

TROCHE ZASTOSOWAŃ WIEDZY O FUNKCJACH
ZADANIE 1
W prostokącie przekątna o
długości 4cm tworzy z krótszym
bokiem kąt 70○. Oblicz pole tego
prostokąta.
Rozwiązanie:
a
sin 70 °=
4
a
0 , 94= ¿⋅4
4
0 , 94⋅4=a
a=3 ,76
cos 70
b
4
b
0,34 / 4
4
0,34 4 b
b 1,36
P=a⋅b=3 ,76⋅1,36≈5 ,11cm 2
Odpowiedź. Pole prostokąta wynosi ok. 5,11 cm2.

9.

Podstawowe wartosci funkcjii trygonometryczne