Odpowiedzi i rozwiązania. Zadania zamknięte

1.

ODPOWIEDZI I ROZWIĄZANIA:
ZADANIA ZAMKNIĘTE:
Zadanie 1 (1pkt) Zadanie 11.
B
Zadanie 2 (1pkt) Zadanie 16.
B
Zadanie 3 (1pkt) Zadanie 22
C
Zadanie 4 (1pkt) Zadanie 5.
A
Zadanie 5 (1pkt) Zad (3/t15/s.208 aksjomat)
C
Zadanie 6 (1pkt) Zadanie32
B
ZADANIA KODOWANE:
Zadanie 7 (2pkt) Zad (9/test XIII/s.203 aksjomat)
720
Zadanie 8 (2pkt) Zad (18/z3/s.29 aksjomat)
398
ZADANIA OTWARTE:
Zadanie 9 (2pkt) Zadanie 48. (2pkt)
Przekształcamy wyrażenie :
n3 n 2 n 3 n2 n 2 1
n 3 n2
n2
2n3 4n 2
.
n2 1 n 3
n2 1 n 3
n2 1 n 3
(1pkt)
Obliczamy granicę:
4
4
n3 2
2
2n 4n
2
n
n
lim 2
lim
lim
2.
n n 1 n 3
n 3
1 3 n
1 3 1 1
n 1 2 1
1 2 1
n n
n n
3
2
Zadanie 10 (3pkt) Zadanie 36.(3pkt)
Przekształcamy równoważnie lewą stronę równości:
L
2 sin 2 sin 88
cos 2 2 cos 88 sin 2
2 sin 2 cos 2
cos 2 2 sin 2 2
1+ 1pkt
sin 4
cos 4
tg 4 P
1pkt
co kończy uzasadnienie
(1pkt)

2.

Zadanie 11A (3pkt) Zadanie 9.(3pkt) ( rozłożyć wielomian n i znaleźć pierwiastki)
1.
Znalezienie pierwiastka i doprowadzenie do postaci iloczynowej: x 1 x 2 x 1 0
2.
Znalezienie pozostałych pierwiastków
x2
1 5
2
x3
1 5
2
2
3.
Obliczenie wartości wyrażenia:
(1pkt)
(1pkt)
2
1 5 1 5
4
a b c 1
2
2
2
2
2
2
(1pkt)
II sposób
Zapiszmy wielomian x 3 2 x 1 w postaci: x 3 2 x 1 ( x a )( x b )( x c ) .
i wykonajmy działania: x 3 2 x 1 x 3 ( a b c ) x 2 ( ab bc ca ) x abc .
1pkt
Wielomiany są równe, gdy maja równe współczynniki przy odpowiednich potęgach. Wobec tego:
a b c 0, ab bc ca 2, abc 1 .
Ponieważ
a b c 2
1pkt
a 2 b 2 c 2 2 ( ab bc ca ) ,
to a 2 b 2 c 2 a b c 2 2 ( ab bc ca ) 0 4 4 .
1pkt
Zadanie 11b (3pkt) Zadanie 100.(3pkt)
f x
x 1
x 2x 2
2
Wyznaczenie pochodnej funkcji f ' ( x)
x 2 2x
x
2
2x 2
2
D D' R .
Wyznaczenie miejsc zerowych funkcji pochodnej x 0 ,
f min ( 2)
Obliczenie wartości ekstremalnych:
f max (0)
(1pkt)
x 2 .
(1pkt)
1
2
(1pkt)
1
2
Zadanie 12 (3pkt) Zadanie 21.(3pkt)
I sposób
Przekształcamy daną nierówność do postaci
8 x 2 4mx 2m 2 12 x 6m 18 0
Stosujemy odpowiednie grupowanie:
4 x 2 12 x 9 4 x 2 4mx m 2 m 2 6m 9 0 ,
(1pkt)
2 x 3 2 2 x m 2 m 3 2 0 .
(1pkt)
Zauważamy, że:
2 x 3 2 0 dla każdej liczby rzeczywistej x ,
2 x m 2 0 dla każdych liczb rzeczywistych x i m ,
m 3 2 0 dla każdej liczby rzeczywistej m .
Stąd 2 x 3 2 2 x m 2 m 3 2 0 dla każdych liczb rzeczywistych
x i m.
(1pkt)

3.

Zatem wykazaliśmy, że dla każdych liczb rzeczywistych x i m prawdziwa jest nierówność
8 x 2 4mx 2m 2 12 x 6m 18 .
II sposób
Przekształcamy daną nierówność do postaci
8 x 2 4mx 2 m 2 12 x 6 m 18 0 ,
8 x 2 4 m 12 x 2 m 2 6 m 18 0 .
Lewą stronę nierówności traktujemy jako trójmian kwadratowy zmiennej
(1pkt)
x z parametrem m:
16m2 96m 144 64m2 192m 576 48m2 288m 432 48 m2 6m 9 ,
2
48 m2 6m 9 48 m 3 .
(1pkt)
Rozważany trójmian kwadratowy 8 x 2 4 m 12 x 2 m 2 6 m 18 ma dodatni współczynnik przy x 2 oraz
niedodatni wyróżnik.
(1pkt)
Z powyższych rozważań wynika, że nierówność 8 x 2 4mx 2m 2 12 x 6m 18 jest prawdziwa dla każdej
liczby rzeczywistej
x i każdej liczby rzeczywistej m .
Zadanie 13 (3pkt) Zadanie (4/zIX /.125 aksjomat) (4pkt)
Za każdą „część” wykresu (1pkt) + (1pkt) + Podanie odpowiedzi (2pkt)
0 –rozwiązań dla
∈ (−∞ , −1)
1 –rozwiązania dla
∈ {−1} ∪ (1, ∞ )
2 –rozwiązania dla
∈ (−1,0 >∪ {1}
3 –rozwiązania dla
∈ (0,1)
Zadanie 14 (4pkt) Zadanie 40.(4pkt)
Równanie możemy przekształcić w sposób równoważny:
sin 2 x 2 sin x cos x 1 0 ,
cos x 2 sin x 1 2 sin x 1 0 ,
2 sin x 1 cos x 1 0 .
(1pkt)
Zauważmy, że ostatnie równanie jest równoważne alternatywie
2 sin x 1 0
lub
(1pkt)
cos x 1 0 .
Równanie (1) jest równoważne równaniu
1
sin x ,
2
sin x sin .
6
Zatem
lub
(1)
x
2k , dla dowolnej liczby całkowitej k
6
7
x 2k , czyli x
2k , dla dowolnej liczby całkowitej k.
6
6
(2)

4.

W zadanym przedziale rozwiązaniem są liczby
5
, .
6
6
Równanie (2) jest równoważne równaniu
cos x 1 ,
(1pkt)
cos x cos .
x 2k , dla dowolnej liczby całkowitej k.
W zadanym przedziale rozwiązaniem są liczby ,
Zatem
.(1pkt)
Zadanie 15 (4pkt) Zadanie 44.(4pkt)
Funkcja f jest szeregiem geometrycznym o ilorazie q
1
takim, że q 1 , zatem
x
1
1
x
1
1 1
x
1
1
1 0
1 0
x
x
1 x
1 x
0
0
x
x
x 1 x 0 x 1 x 0
Wyznaczenie dziedziny:
x ( , 1) (0, )
D ( , 1) (1, )
Obliczenie sumy: x 1
Z tego wynika, że f ( x )
(1pkt)
x ( .0) (1, )
x 1 x 1 x 1
x 1 x2 x
2 3 ...
1
x
x 1
x
x
1
x
x2 x
x 1
(1pkt)
(1pkt)
dla x ( , 1) (1, )
Wyznaczamy argumenty, dla których funkcja f przyjmuje wartość
6 nie większe niż 6
x2 x
6 0
x 1
x 2 x 6x 6
0
x 1
x
2
5x 6 x 1 0
x 2 x 3 x 1
f ( x) 6 x ( ,1 2,3
Odp : D f ( x) 6 x ( , 1) 2,3
(1pkt)
Zadanie 16 (4pkt) Zadanie 57.(4pkt)
I sposób
Obwód trapezu L wyraża się wzorem L a b 2c .
Trapez jest opisany na okręgu, więc sumy długości jego przeciwległych boków są równe.
Oznacza to, że a b 2c . Wynika z tego, że L 4c .
Wyznaczmy długość boku c.
(1pkt)

5.

Wiemy, że promień okręgu r
91
. Tak więc wysokość trapezu h 2 r 91 .
2
Rozważmy trójkąt o bokach długości x, h i c, gdzie x
(1pkt)
a b
3.
2
(1pkt)
Z twierdzenia Pitagorasa mamy
c 91 9 ,
c 10 .
Wynika z tego, że obwód trapezu
(1pkt)
L 40 .
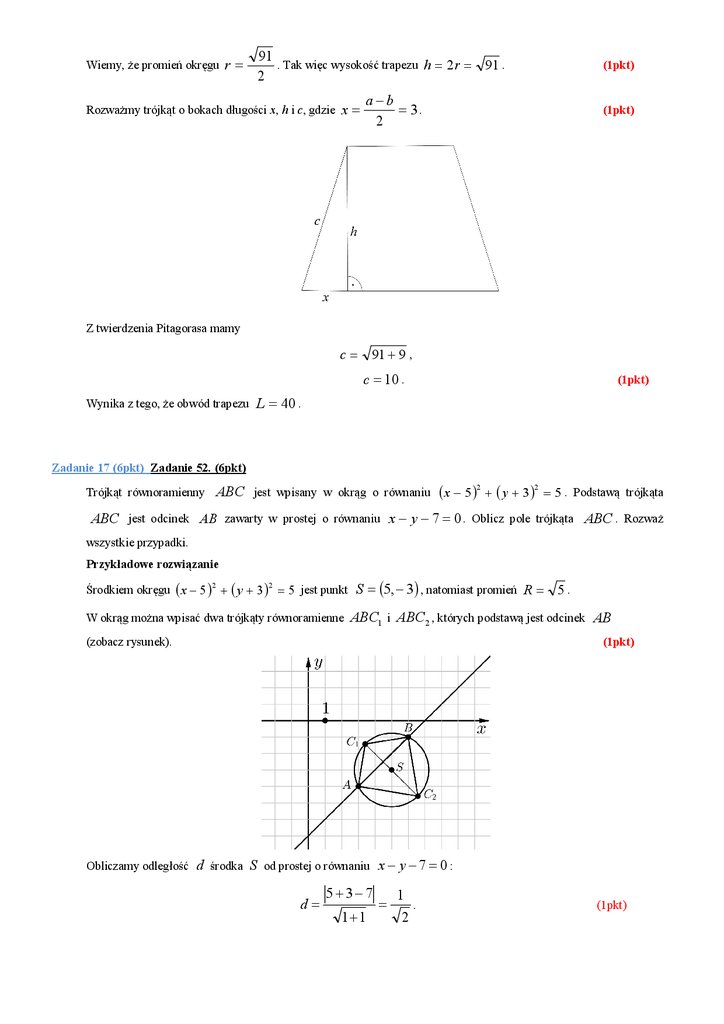
Zadanie 17 (6pkt) Zadanie 52. (6pkt)
Trójkąt równoramienny
ABC jest wpisany w okrąg o równaniu x 5 2 y 3 2 5 . Podstawą trójkąta
ABC jest odcinek AB zawarty w prostej o równaniu x y 7 0 . Oblicz pole trójkąta ABC . Rozważ
wszystkie przypadki.
Przykładowe rozwiązanie
Środkiem okręgu x 5 2 y 3 2 5 jest punkt S 5, 3 , natomiast promień R
W okrąg można wpisać dwa trójkąty równoramienne
5.
ABC1 i ABC2 , których podstawą jest odcinek AB
(zobacz rysunek).
(1pkt)
Obliczamy odległość d środka S od prostej o równaniu x y 7 0 :
d
5 3 7
1 1
1
.
2
(1pkt)

6.

Oznaczmy przez a
1
AB (zobacz rysunek obok).
2
Z twierdzenia Pitagorasa możemy zapisać:
a2 d 2 R2 .
Zatem
a 5
1
3 3 2
, czyli AB 3 2 .
2
2
2
(1pkt)
Uwaga
Długość odcinka AB możemy też obliczyć, wyznaczając najpierw współrzędne punktów przecięcia danej prostej i
okręgu. Wystarczy rozwiązać układ równań:
x 5 2 y 3 2 5
y x 7
Wysokość trójkąta ABC1 poprowadzona z wierzchołka C1 jest równa
h1 R d 5
Wysokość trójkąta
1
2
.
(1pkt)
ABC2 poprowadzona z wierzchołka C2 jest równa
h2 R d 5
1
.
2
(1pkt)
1
5
3 2
3 10 3
2
Z tego wynika, że pole trójkąta ABC1 : P1
2
2
oraz pole trójkąta
ABC2 :
1
5
3 2
3 10 3
2
.
P2
2
2
(1pkt)
Zadanie 18 A (8pkt) Zadanie 90.(7pkt)
H
a
Wprowadzamy oznaczenia:
a — krawędź podstawy graniastosłupa, H — wysokość graniastosłupa.
Z warunków zadania mamy: 6a 3H 12 , stąd H 4 2a .
Zapisujemy wzór na objętość graniastosłupa:
(1pkt)

7.

V
V
a2 3
a2 3
H
4 2a ,
4
4
3 3
3
a 3a 2
a 3 2a 2
2
2
dla 0 a 2 .
Rozważamy funkcję
(1pkt)
(1pkt)
f (a) a3 2a 2 określoną dla każdej liczby rzeczywistej a .
Obliczamy pochodną tej funkcji:
f (a) 3a2 4a .
(1pkt)
4
a2 .
3
Znajdujemy miejsca zerowe pochodnej: a 3a 4 0 , stąd a1 0 ,
(1pkt)
Ponadto:
4
3
f ( a ) 0 dla a należącego do przedziału 0, ,
f ( a ) 0 w każdym z przedziałów , 0 oraz , .
4
3
Zatem funkcja f jest rosnąca w przedziale
Ponieważ
V a
0,
4
4
i malejąca w każdym z przedziałów ,0 oraz
, .
3
3
3
f (a) dla 0 a 2 , to w przedziale 0, 2 funkcja V a ma ekstremum w tym
2
samym punkcie, w którym ma je funkcja
dodatnią) wynika, że w punkcie
a
f (a ) . Stąd oraz z monotoniczności (współczynnik
4
funkcja V przyjmuje największą wartość.
3
Szukane długości boków graniastosłupa są więc równe: a
Objętość graniastosłupa jest równa
V
3
jest liczbą
2
(1pkt)
4
4 4
, H 4 2 .
3
3 3
16 3
.
27
(1pkt)
Zadanie 18 B (7pkt) Zadanie 56.
I sposób
Wprowadzamy oznaczenia jak na rysunku obok.
Korzystamy z jedynki trygonometrycznej: cos 2 1
Wybieramy przypadek dla kąta ostrego: cos
5 4
.
9 9
2
.
3
Wykorzystujemy twierdzenie cosinusów do wyznaczenia boku AC x .
1pkt

8.

x 2 36 64 96
2
,
36
3
x 6.
Z twierdzenia sinusów otrzymujemy: R
Obliczamy pole trójkąta i jego obwód:
1pkt
x
2 sin
P
6
5
2
3
9
9 5
.
5
5
1
5
48
8 5 ,
2
3
L 20 .
Obliczamy promień okręgu wpisanego:
Wyznaczamy stosunek promieni:
r
R 9 5 5
9
.
r
5 4 5 4
5 4
.
9 9
2
.
3
Wykorzystujemy twierdzenie cosinusów do wyznaczenia boku AC x .
x 2 36 64 96
2
36 ,
3
x 6.
Obliczamy pole trójkąta i połowę jego obwodu:
P
1pkt
1pkt
II sposób
Wybieramy przypadek dla kąta ostrego: cos
1pkt
1pkt
P
8 5
4 5
.
1
10
5
L
2
Korzystamy z jedynki trygonometrycznej: cos 2 1
1pkt
1
5
48
8 5 , p 10 ,
2
3
AB BC AC
AB BC AC p 6 8 6 10 9
R
4P
.
P
r
4P 2
4 64 5
4
p