Похожие презентации:
Транспортная задача. Методы нахождения начального решения транспортной задачи (лекция 4)
1.
Смирнов Вадим ЕвгеньевичМатематическое
моделирование
https://vk.com/ranepa_infteh_smirnov
1
2.
Смирнов Вадим ЕвгеньевичМатематическое
моделирование
Лекция 4
Транспортная задача. Методы
нахождения начального
решения транспортной задачи
2
3.
Математическая постановка задачиТранспортная задача - это специальный вид
задачи линейного программирования. Для решения
транспортной задачи можно использовать методы
решения задач линейного программирования,
однако ввиду специфического вида задачи, были
построены алгоритмы специально для решения
этой задачи.
Общая
постановка
транспортной
задачи
заключается в определении оптимального плана
перевозок некоторого однородного груза из пунктов
отправления
A1,
A2,...,
Am
в
пункты
назначения B1, B2,..., Bn. Критерий оптимальности
берется минимальная стоимость перевозки или
минимальное время доставки груза.
4.
Математическая постановка задачиРассмотрим транспортную задачу, где в качестве
критерия оптимальности взята минимальная
стоимость перевозок всего груза. Обозначим
через Сij тарифы перевозки единицы груза из
пункта отправления i в пункт назначения j.
Обозначим через Ai запасы груза i-м пункте
отправления, а через Bj потребности груза j-м
пункте назначения, а через Xj количество единиц
груза переводимого из пункта отправления i в пункт
назначения j.
5.
Математическая постановка задачиТогда математическая модель
задачи состоит в определении
значения функции
транспортной
минимального
(1.1)
при условиях
(1.2)
(1.3)
(1.4)
Поскольку удовлетворяется условия (1.2)−(1.4), то
обеспечивается доставка необходимого количества
груза в каждый из пунктов назначения, вывоз груза
из всех пунктов отправления, а также исключаются
обратные перевозки.
6.
Математическая постановка задачиОпределение
1.
Любое
неотрицательное
решение Xij=∥xij∥ (i=1,..,m; j=1,...,n) систем (1.2) и
(1.3)
называется
допустимым
планом транспортной задачи.
Определение 2. План Xij* = ∥xij * ∥ (i=1,..,m; j=1,...,n)
при котором функция (1.1) принимает минимальное
значение, называется оптимальным планом
транспортной задачи.
7.
Математическая постановка задачиЕсли сумма груза у поставщиков равно общей
сумме потребностей в пунктах назначения:
(1.5)
то
модель
транспортной
задачи
называется закрытой (или сбалансированной).
Если (1.5) не удовлетворяется, то модель
транспортной
задачи
называется открытой (или несбалансированной).
8.
Математическая постановка задачиТеорема 1. Для разрешимости транспортной
задачи
необходимо
и
достаточно,
чтобы
выполнялось условие (1.5).
В случае превышения запаса над потребностью,
т.е. при
вводится фиктивный (n+1)-ый пункт назначения с
потребностью
Соответствующие тарифы считаются равными
нулю: ci n+1=0 (i=1,...,m). После этих преобразований
получим закрытую модель транспортной задачи.
9.
Математическая постановка задачиАналогично, при
вводится фиктивный (m+1) пункт отправления с
грузом
а тарифы полагаются равными нулю: cm+1j=0
(j=1,...,n). После этих преобразований получим
закрытую модель транспортной задачи.
Мы будем рассматривать закрытую модель
транспортной
задачи.
Если
же
модель
транспортной задачи является открытой, то с
помощью
вышеизложенных
преобразований
строим закрытую модель транспортной задачи.
10.
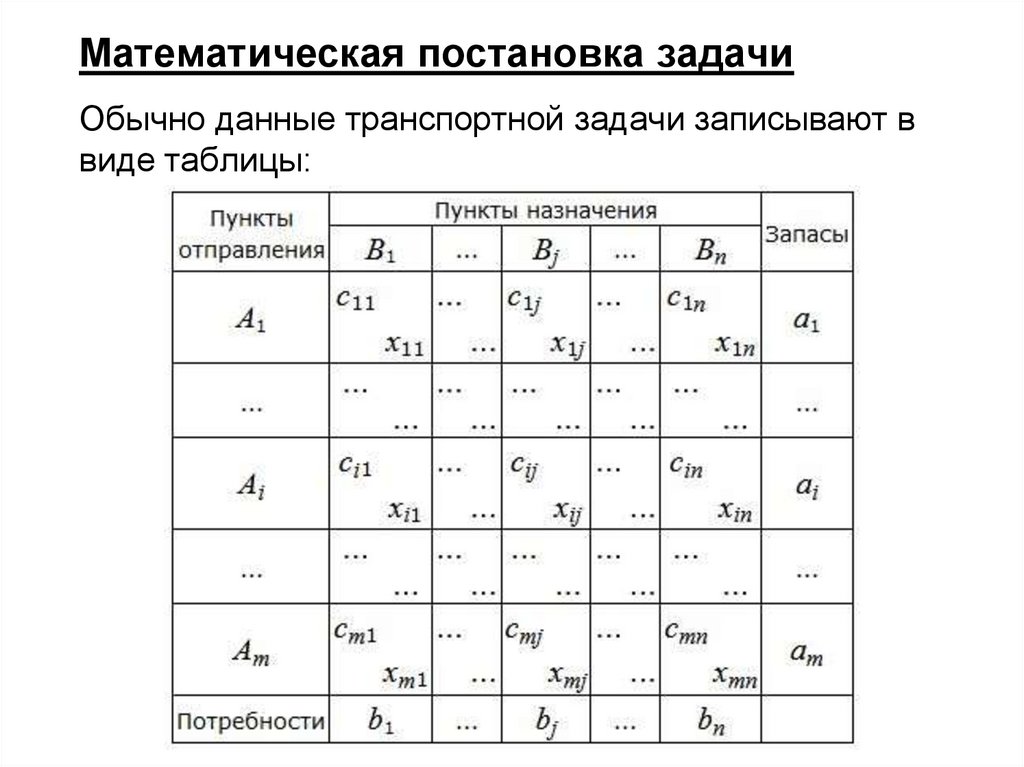
Математическая постановка задачиОбычно данные транспортной задачи записывают в
виде таблицы:
11.
Математическая постановка задачиЧисло переменных Xij равно mn, где m число
пунктов отправления, а n число пунктов
назначения. Число уравнений в (1.2) и (1.3)
равно m+n. Так как мы рассматриваем закрытую
модель
транспортной
задачи
(выполняется
равенство (1.5)), то число линейно независимых
уравнений равно m+n−1. Следовательно опорный
план транспортной задачи может иметь не
более m+n−1 отличных от нуля неизвестных.
Если в опорном плане количество отличных от нуля
компонентов равно в точности m+n−1, то опорный
план называется невырожденным, а если меньше
− то вырожденным.
12.
Математическая постановка задачиДля решения транспортной задачи сначала
определяется начальный опорный план, а затем
определяется оптимальный план путем улучшения
текущего опорного плана.
Для определения начального опорного плана
существует несколько методов. Мы рассмотрим три
метода. Метод северно-западного угла, метод
минимального элемента и метод аппроксимации
Фогеля.
13.
Определение опорного планаОпорный план транспортной задачи находим
следующим образом. На каждом шаге в таблице
условий задачи заполняем одну клетку, которая
называется занятой. Обозначим через Kij клетку,
где i - номер пункта отправления (строка), j - номер
пункта назначения (столбец). Клетку Kij заполняем
так,
чтобы
удовлетворялись
полностью
потребности
пункта
назначения
j,
либо
обеспечивался полный вывоз груза из пункта
отправления i.
14.
Определение опорного планаВ первом случае временно исключаем из
рассмотрения столбец j и изменяем запас груза
пункта отправления i. Во втором случае временно
исключаем из рассмотрения строку i и изменяем
потребность груза пункта назначения j. Далее
повторяем процедуру с таблицей условий с
исключенной строкой или столбцом.
В m+n−1-ом шаге получаем задачу с одним пунктом
отправления и одним пунктом назначения.
Остается
свободной
одна
клетка.
Запасы
оставшегося пункта отправления будут равны
потребностям пункта назначения. Заполнив эту
клетку заканчиваем m+n−1-ый шаг и получаем
опорный план.
15.
Определение опорного планаЕсли на некотором шаге (но не на последнем)
потребности очередного пункта назначения равны
запасам пункта отправления, то временно
исключаем из рассмотрения либо столбец, либо
строку (только одно из двух). Тогда либо запасы
данного пункта отправления, либо потребности
данного пункта назначения считаем равным нулю.
Этот нуль при очередном шаге записываем в
очередную заполняемую клетку. Данный подход
обеспечивает ровно m+n−1 занятых клеток, что
обеспечивает возможность проверки полученного
опорного плана на оптимальность и нахождение
оптимального плана.
16.
Метод северо-западного углаПри нахождении опорного плана транспортной
задачи
методом
северно-западного
угла,
заполнение клеток таблицы условий начинают с
верхней левой клетки K11). Рассмотрим метод на
конкретном примере.
Пример 1. На три базы A1, A2, A3 поступил
очередной груз в количествах равных 140, 160, 120
ед. Этот груз требуется перевезти в четыре пунктов
назначения B1, B2, B3, B4 в количествах 150, 90, 100,
80. Тарифы перевозок представлена матрицей
Найти план перевозок данной транспортной задачи.
17.
Метод северо-западного углаРешение. Запишем все данные в таблицу условий:
Число пунктов отправления m=3, а число пунктов
назначения n=4. Следовательно, опорный план
задачи
определяется
числами,
стоящими
в m+n−1=3+4−1=6 заполненных клетках таблицы.
18.
Метод северо-западного углаНаличие
груза
у
∑Ai=140+160+120=420.
поставщиков
равно:
Общая потребность в грузе в пунктах назначения
равна: ∑Bj=150+90+100+80=420.
∑Ai=∑Bj. Модель транспортной задачи является
закрытой. Следовательно она разрешима.
Найдем опорный план задачи методом севернозападного угла.
19.
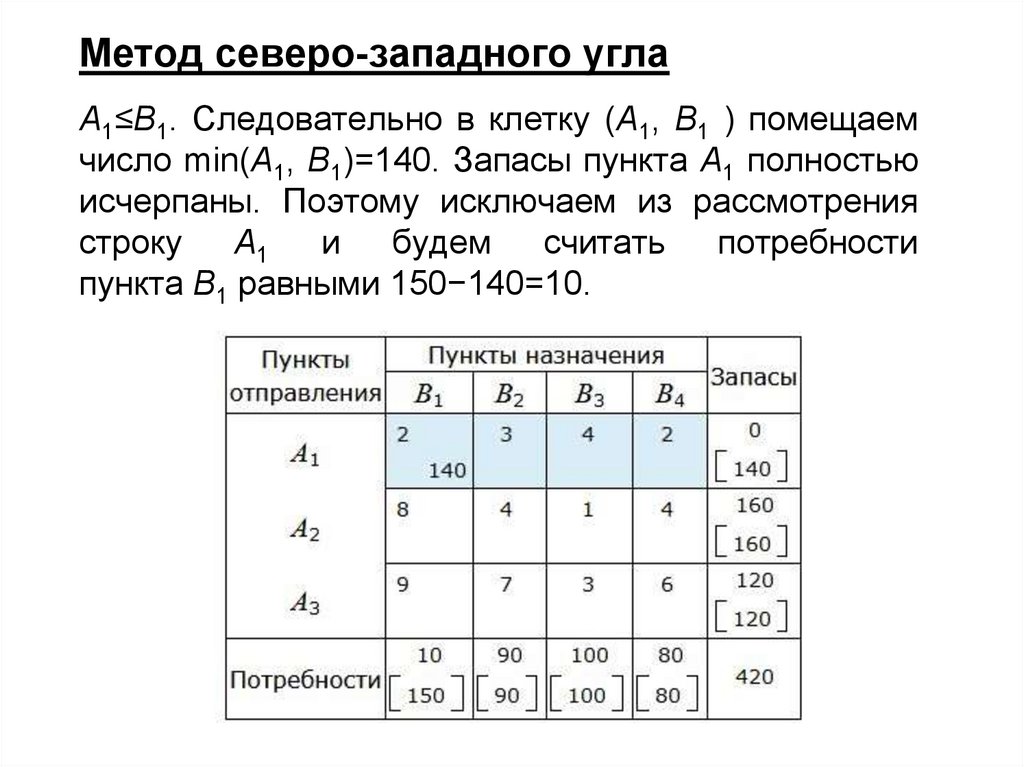
Метод северо-западного углаA1≤B1. Следовательно в клетку (A1, B1 ) помещаем
число min(A1, B1)=140. Запасы пункта A1 полностью
исчерпаны. Поэтому исключаем из рассмотрения
строку
A1
и
будем
считать
потребности
пункта B1 равными 150−140=10.
20.
Метод северо-западного углаA2>B1. Следовательно в клетку (A2, B1) помещаем
число
min(A2,
B1)=10.
Потребности
пункта B1 полностью удовлетворены. Поэтому
исключаем из рассмотрения столбец B1 и будем
считать запасы пункта A2 равными 160−10=150.
21.
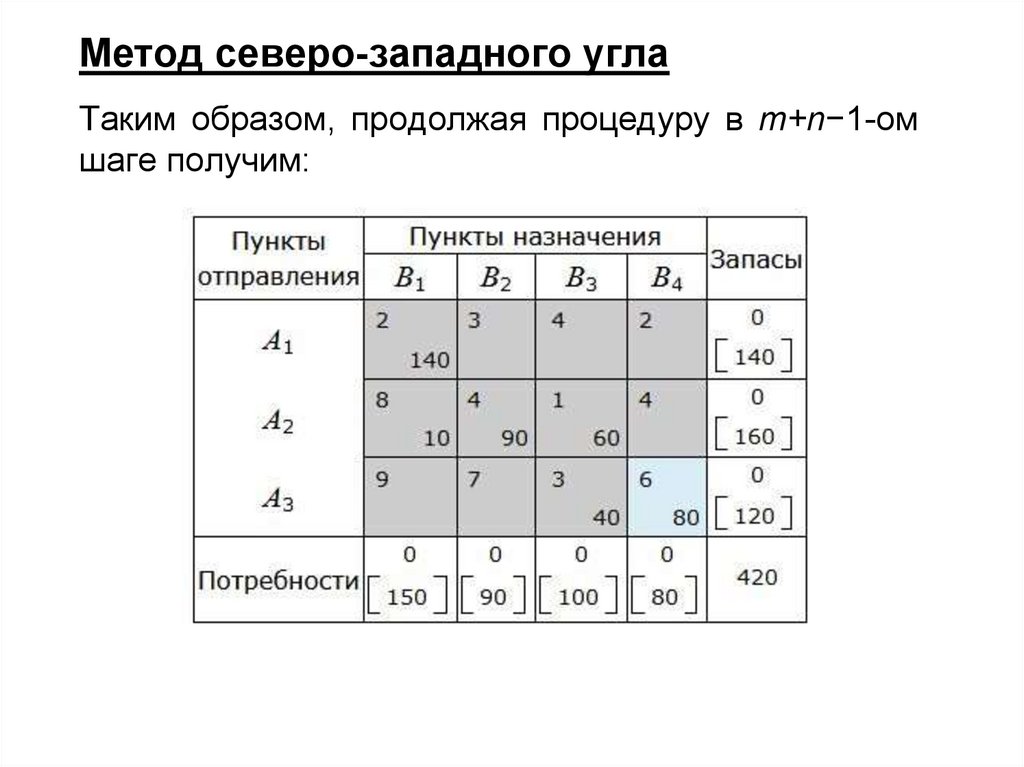
Метод северо-западного углаТаким образом, продолжая процедуру в m+n−1-ом
шаге получим:
22.
Метод северо-западного углаЗапишем полученный опорный план:
При этом плане стоимость перевозок вычисляется
так:
F = 2·140 + 8·10 + 4·90 + 1·60 + 3·40 + 6·80 = 1380.
23.
Метод минимального элементаВ отличие от метода северно-западного угла, в
методе минимального элемента выбор пунктов
отправления и пунктов назначения производится
ориентируясь на тарифы перевозок, т.е. в каждом
шаге нужно выбрать клетку с минимальным
тарифом перевозок. Если таких клеток несколько,
то выбираем один из них. Надо отметить, что при
данном методе определения заполняемой клетки,
стоимость перевозок как правило бывает меньше,
чем при методе северно-западного угла. Поэтому
целесообразно начальный опорный план найти
методом минимального элемента.
Рассмотрим метод минимального элемента на
примере.
24.
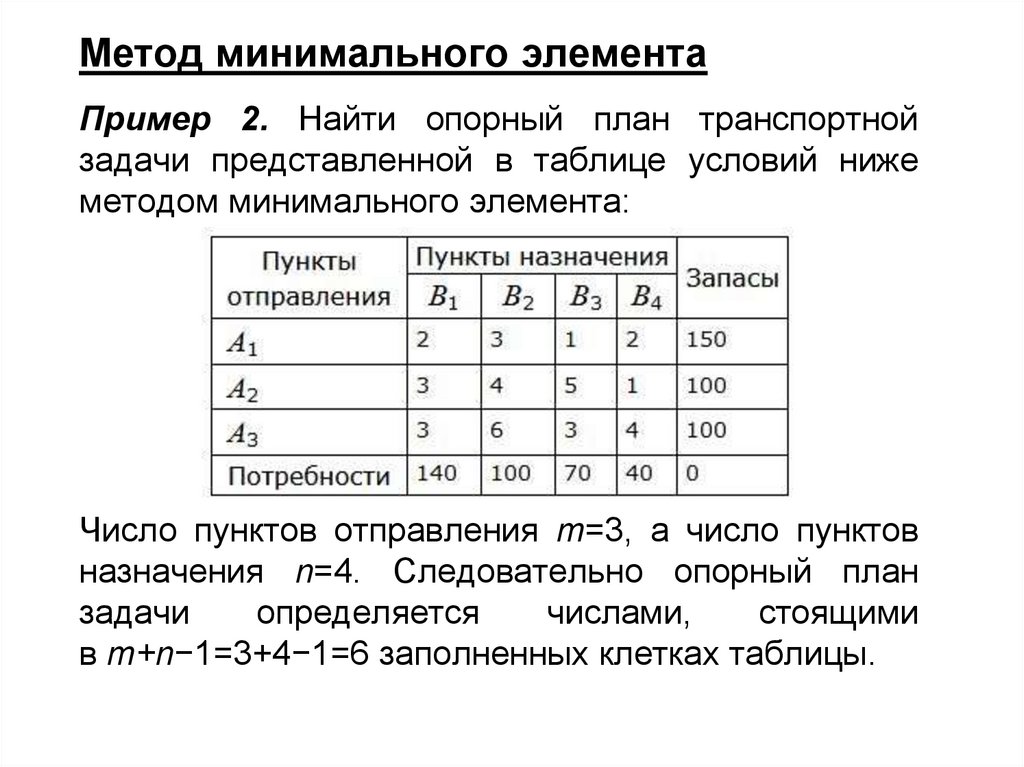
Метод минимального элементаПример 2. Найти опорный план транспортной
задачи представленной в таблице условий ниже
методом минимального элемента:
Число пунктов отправления m=3, а число пунктов
назначения n=4. Следовательно опорный план
задачи
определяется
числами,
стоящими
в m+n−1=3+4−1=6 заполненных клетках таблицы.
25.
Метод минимального элементаТарифы перевозок единицы груза из кажного
пункта отправления во все пункты назначения
задаются матрицей
Наличие груза у поставщиков равно:
∑Ai = 150 + 100 + 100 = 350
Потребность в грузе в пунктах назначения равна:
∑Bi = 140 + 100 + 70 + 40 = 350
∑Ai = ∑Bi Модель транспортной задачи является
закрытой. Следовательно она разрешима.
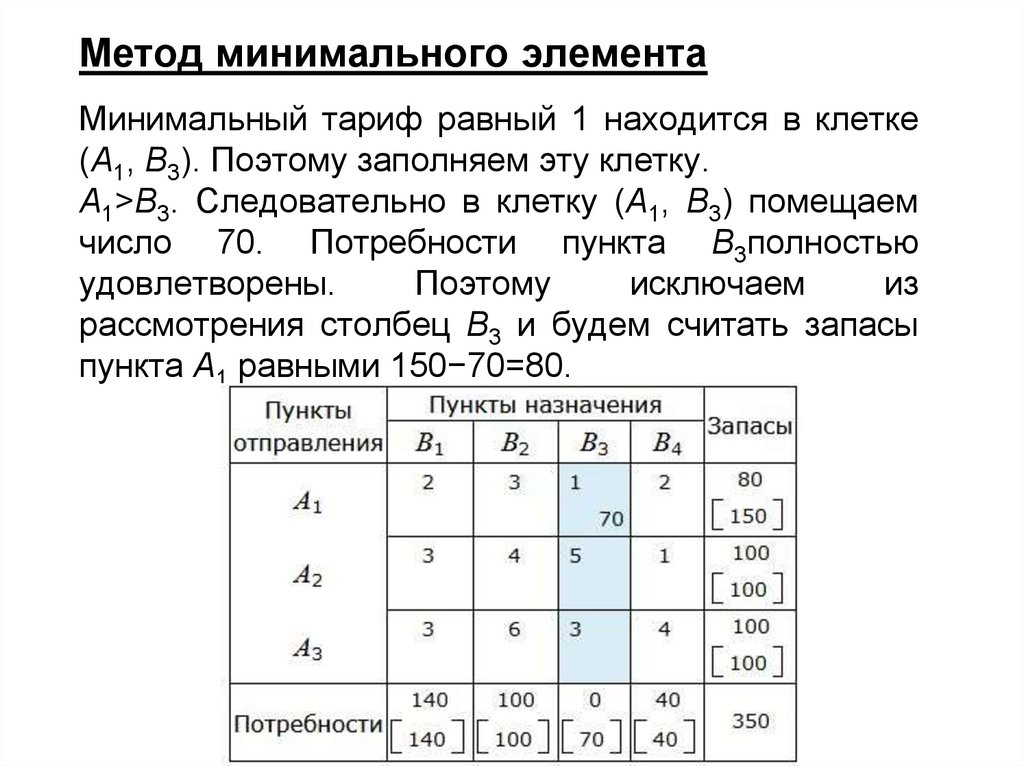
26.
Метод минимального элементаМинимальный тариф равный 1 находится в клетке
(A1, B3). Поэтому заполняем эту клетку.
A1>B3. Следовательно в клетку (A1, B3) помещаем
число 70. Потребности пункта B3полностью
удовлетворены.
Поэтому
исключаем
из
рассмотрения столбец B3 и будем считать запасы
пункта A1 равными 150−70=80.
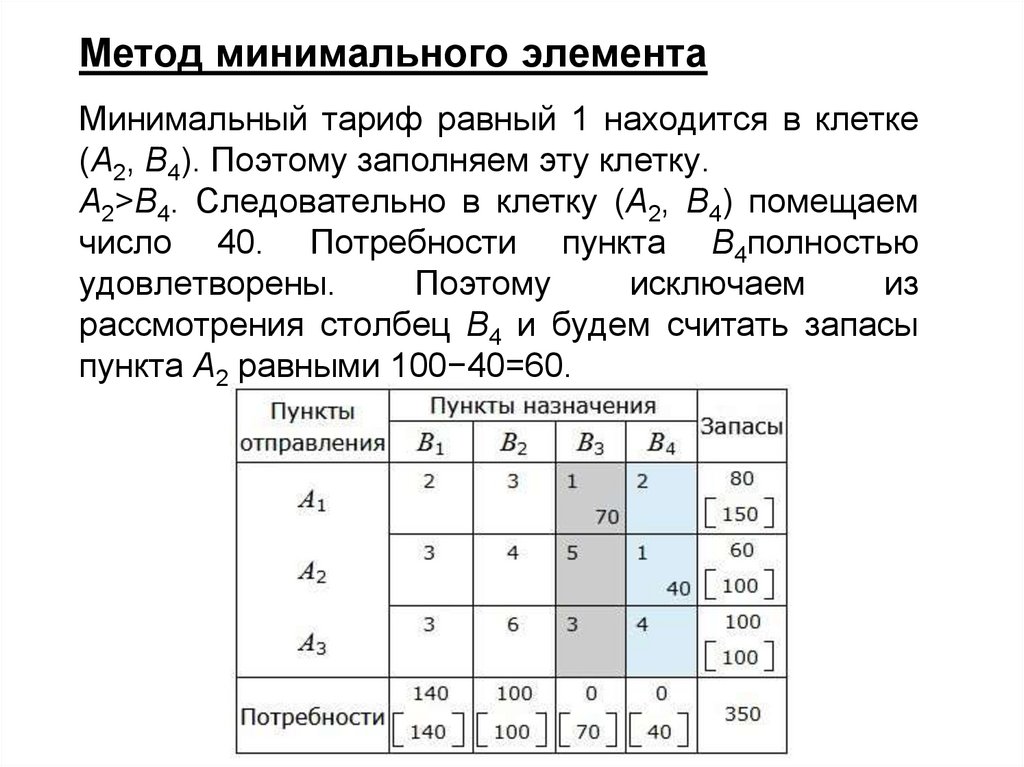
27.
Метод минимального элементаМинимальный тариф равный 1 находится в клетке
(A2, B4). Поэтому заполняем эту клетку.
A2>B4. Следовательно в клетку (A2, B4) помещаем
число 40. Потребности пункта B4полностью
удовлетворены.
Поэтому
исключаем
из
рассмотрения столбец B4 и будем считать запасы
пункта A2 равными 100−40=60.
28.
Метод минимального элементаТаким образом, продолжая процедуру в m+n−1-ом
шаге получим:
29.
Метод минимального элементаЗапишем полученный опорный план:
При этом стоимость перевозок вычисляется так:
F = 2·80 + 1·70 + 3·60 + 1·40 + 3·0 + 6·100 = 1050
30.
Метод аппроксимации ФогеляСуть метода аппроксимации Фогеля заключается в
следующем. Для каждой строки и для каждого
столбца
находим
разности
между
двумя
записанными в них минимальными тарифами.
Полученные разности записываем в специально
отведенные для этого столбце и в строке в таблице
условий задачи.
Среди
указанных
разностей
выбираем
максимальную. В строке (или в столбце), которой
данная разность соответствует, определяем
минимальный тариф. Клетку, в которой он записан
заполняем на данной итерации.
31.
Метод аппроксимации ФогеляЕсли минимальный тариф одинаков для нескольких
клеток данной строки (столбца), то для заполнения
выбираем ту клетку, которая соответствует
наибольшей разности между двумя минимальными
тарифами в данном столбце (строке).
Применение
метода
аппроксимации
Фогеля
позволяет получить либо опорный план, близкий к
оптимальному, либо сам оптимальный план.
32.
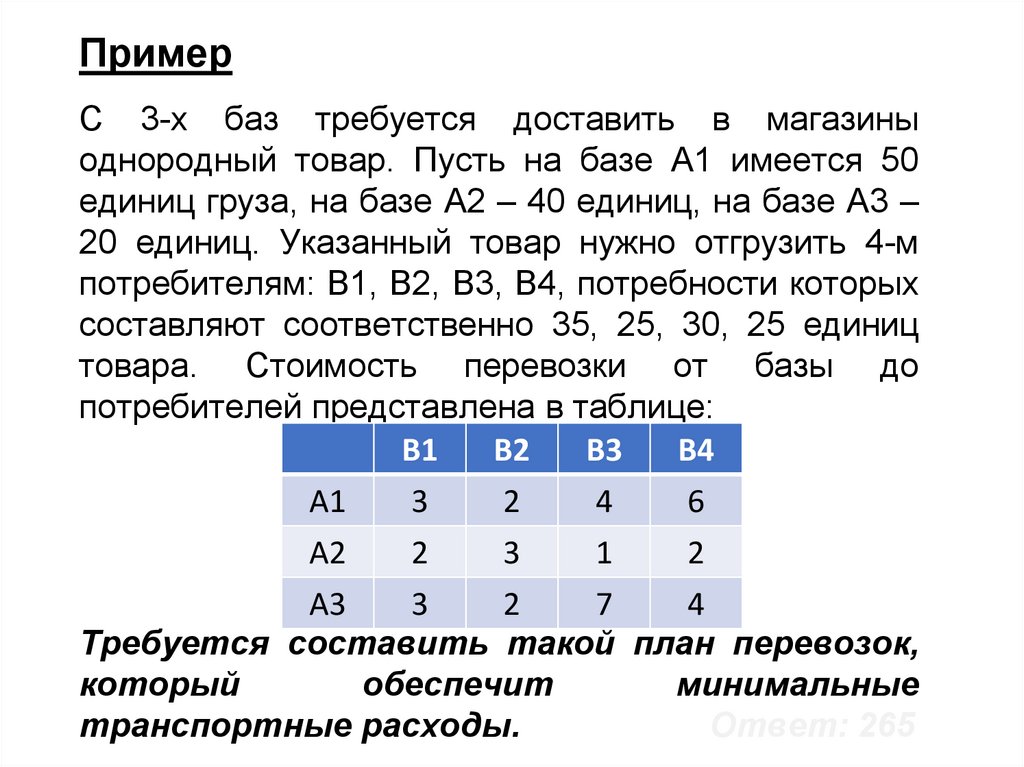
ПримерС 3-х баз требуется доставить в магазины
однородный товар. Пусть на базе А1 имеется 50
единиц груза, на базе А2 – 40 единиц, на базе А3 –
20 единиц. Указанный товар нужно отгрузить 4-м
потребителям: В1, В2, В3, В4, потребности которых
составляют соответственно 35, 25, 30, 25 единиц
товара. Стоимость перевозки от базы до
потребителей представлена в таблице:
B1
B2
B3
B4
A1
3
2
4
6
A2
2
3
1
2
A3
3
2
7
4
Требуется составить такой план перевозок,
который
обеспечит
минимальные
транспортные расходы.
Ответ: 265

























 Математика
Математика








