Транспортная задача. (Лекции 10,11)

1. ТРАНСПОРТНАЯ ЗАДАЧА

Лекции 10,11

2.

Транспортная задача является
частным случаем задачи линейного
программирования и может быть
решена симплекс-методом.
Однако, в силу особенностей этой
задачи, она решается с помощью
так называемого
распределительного метода и его
модификаций

3.

Общая постановка транспортной задачи
состоит в определении оптимального плана
перевозок некоторого однородного груза из m
пунктов отправления А1, А2,…, Аm в
n пунктов назначения B1, B2,…,Bn.
При этом в качестве критерия
оптимальности берется либо минимальная
стоимость перевозок всего груза, либо
минимальное время его доставки.

4.

Рассмотрим транспортную задачу, в которой в
качестве критерия оптимальности берется
минимальная стоимость перевозок всего
груза. Обозначим через cij тарифы или
стоимости перевозки единицы груза из i-го
пункта отправления в j-й пункт назначения,
через ai – запасы груза в i-м пункте
отправления, через b j – потребности в грузе
j-ым пунктом назначения, через xij–
количество единиц груза, перевозимого из i-го
пункта отправления в j-й пункт назначения
(перевозки).

5. Математическая модель транспортной задачи

m
n
Найти F = åå cij xij ® min
i =1 j =1
при ограничениях
m
ì
ïå xij = b j , j = 1, n
ï i =1
ï n
íå xij = ai , i = 1, m
ï j =1
ïx ³ 0
ï ij
î

6.

Первое ограничение
ì
íå xij = b j , j = 1, n
î i =1
m
означает, что все потребности должны быть
удовлетворены , а второе -
ì n
íå xij = ai , i = 1, m
,
î j =1
что все запасы должны быть перевезены.

7.

Определение. Всякое неотрицательное
решение системы ограничений транспортной
задачи, определяемое матрицей размера
m×n
æ x11 x12 ...x1n ö
ç
÷
x21 x22 ...x2 n ÷
ç
X=
ç ................. ÷
ç
÷
è xm1 xm 2 ...xmn ø
,
называют допустимым решением (или
планом) транспортной задачи.

8.

Определение.
План
*
*
ij m´n
X = (x )
,
при котором целевая функция
принимает минимальное значение,
называется оптимальным.

9.

Тарифы или стоимости перевозок единицы
груза cij также задаются матрицей, которая
называется матрицей транспортных издержек
или матрицей стоимостей
æ c11c12 ...c1n ö
ç
÷
c
c
...
c
21
22
2n ÷
ç
C=
ç ................. ÷
ç
÷
è cm1cm 2 ...cmn ø

10. Транспортная таблица

11. Необходимое и достаточное условие разрешимости транспортной задачи

Для разрешимости транспортной задачи
необходимо и достаточно, чтобы запасы груза
в пунктах отправления были равны
потребностям в грузе в пунктах назначения,
то есть, чтобы выполнялось равенство
m
åa
i =1
i
=
n
åb
j =1
j
--балансовые условия.

12.

При выполнении этого условия модель
транспортной задачи называется
закрытой. Если балансовое условие не
выполняется, то есть
m
n
,
å ai ¹ å b j
i =1
j =1
то модель транспортной задачи
называется открытой.

13.

В случае открытой транспортной задачи
выполнение балансового условия
достигается введением фиктивного
поставщика или фиктивного
потребителя с соответствующими
тарифами, равными нулю.

14.

Любое решение транспортной задачи
представляет собой распределение
перевозок xij в транспортной таблице.
Оптимальному решению транспортной
задачи соответствует оптимальное
распределение перевозок.
Перераспределение перевозок в
транспортной таблице осуществляется
до тех пор, пока не будет найдено
оптимальное распределение перевозок.

15. Пример

16.

Все грузы должны быть перевезены, поэтому
4
åx
j =1
ij
= ai , i = 1,3
Это три первых уравнения.
Все потребности должны быть удовлетворены
3
и, значит,
åx
i =1
ij
= b j , j = 1, 4.
Это четыре последних уравнения.
Здесь закрытая модель: сумма запасов равна
сумме потребностей.

17.

А целевую функцию составили по
матрице С - матрице тарифов
перевозок.

18. Пример. Задача организации оптимального снабжения .

Три фермерских хозяйства A1 , A2 , A3
ежедневно могут доставлять в город
соответственно 60, 60 и 50 ц молока
для обеспечения пяти торговых точек :
B1 , B2 , B3 , B4 , B5
Стоимость перевозки 1ц молока и
потребности торговых точек в молоке
указаны в таблице

19. Таблица

20. Экономико-математическая модель задачи.

Переменные : xij (i = 1,3, j = 1,5)
- количество молока , поставляемое i-м
фермерским хозяйством в j-ю торговую точку.
Целевая функция –суммарные транспортные
издержки, которые необходимо
минимизировать
F = 7 x11 + 6 x12 + 8 x13 + 10 x14 + 12 x15 +
+9 x21 + 5 x22 + 7 x23 + 4 x24 + 6 x25 +
+6 x31 + 8 x32 + 4 x33 + 9 x34 + 7 x35 ® min

21.

Эта задача является задачей открытого
типа, так как запасы молока у
фермерских хозяйств (поставщиков)
больше потребностей в молоке у
торговых точек. В этом случае
изменяется вид системы ограничений.

22. Функциональные ограничения:

По поставщикам (их 3)
по потребителям (их
5)
ì x11 + x12 + x13 + x14 + x15 £ 60 ï
í x21 + x22 + x23 + x24 + x25 £ 60
ï x + x + x + x + x £ 50
î 31 32 33 34 35
ì x11 + x21 + x31 = 30,
ï
ï x12 + x22 + x32 = 20,
ï
í x13 + x23 + x33 = 55,
ï
ï x14 + x24 + x34 = 20,
ïî x15 + x25 + x35 = 25.
xij ³ 0.

23. Этапы решения транспортной задачи

• Составляют математическую модель
задачи.
• Находят исходное опорное решение.
• Проверяют это решение на
оптимальность.
• Переходят от одного опорного решения
к другому.

24.

Будем называть переменные , стоящие
в занятых клетках распределительной
или транспортной таблицы, базисными,
а переменные находящиеся в пустых
клетках, свободными.

25. Определение исходного допустимого решения

1. Метод «северо-западного угла»
Метод заключается в том, что
заполнение клеток таблицы начинают с
левой верхней клетки (северо-западная
часть таблицы) для перевозки x11 и
продолжают вниз и вправо, заканчивая
клеткой для перевозки xmn .
При этом способе распределения на
тарифы cij
не обращают внимания.

26.

2. Метод «наименьшей стоимости»
Метод заключается в том, что
заполнение клеток таблицы начинают с
клетки, имеющей наименьшую
стоимость перевозки. Если таких клеток
несколько, то следует выбрать любую
из них.

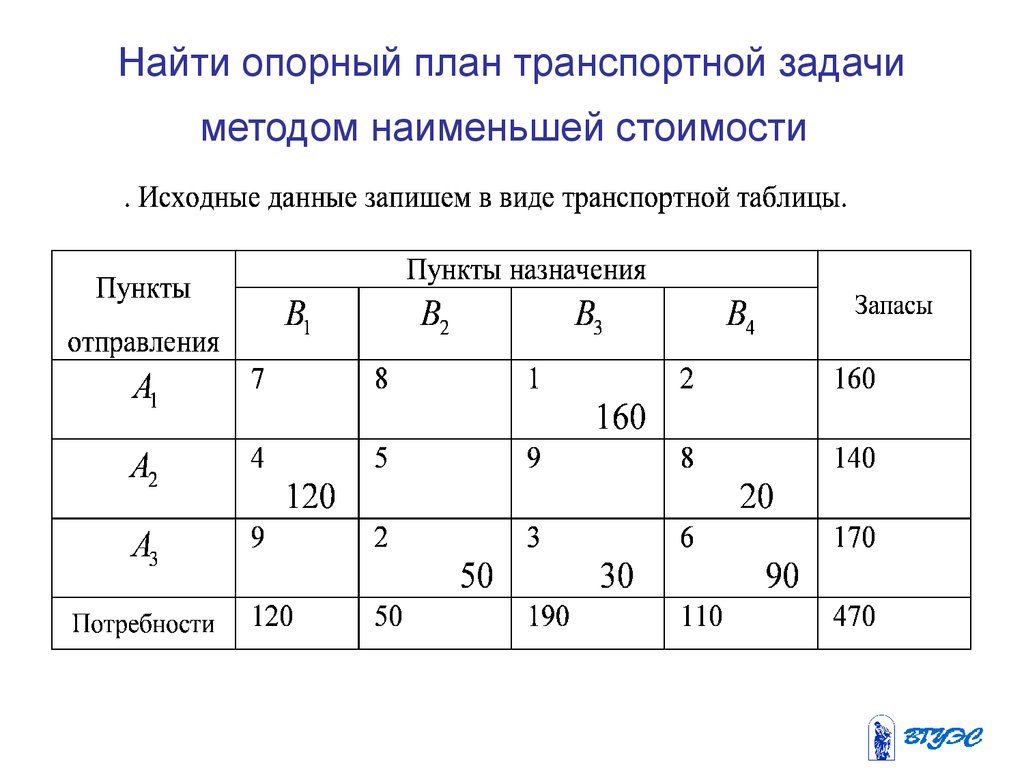
27. Найти опорный план транспортной задачи методом наименьшей стоимости

28.

Минимальный тариф, равный 1 ,
находится в клетке x13 .
Положим x13 = 160 . Запишем это
значение в соответствующую клетку и
временно исключим из рассмотрения
строку A1 .
Потребности пункта назначения B3
считаем временно равными 30 ед.

29.

В оставшейся части таблицы с двумя
строками A2 и A3 и c четырьмя
столбцами клетка с наименьшим
тарифом находится на пересечении
строки A3 и столбца B2 , где c32 = 2.
Положим x32 = 50. Внесем это значение
в соответствующую клетку таблицы.

30.

Временно исключим из рассмотрения
столбец B2 и будем считать запасы
пункта A3 равными 120 ед. После
этого рассмотрим оставшуюся часть
таблицы с двумя строками A2 и A3 и
тремя столбцами B1 , B3 и B4 . В ней
минимальный тариф находится в клетке
на пересечении строки A3 и
столбца B3 и равен 3.

31.

Заполним описанным выше способом
эту клетку и аналогично заполним ( в
определенном порядке) клетки,
находящиеся на пересечении строки A2
и столбца B4 .

32.

В результате получим опорный план
0 160 0 ö
æ 0
ç
÷
X = ç120 0
0 20 ÷
ç 0 50 30 90 ÷
è
ø
При данном плане перевозок общая
стоимость перевозок составляет .
F = 1×160 + 4 ×120 + 8 × 20 + 2 × 50 + 3 × 30 + 6 × 90 = 1530

33. Условие невырожденности плана

Если число заполненных клеток равно
m + n – 1, то план является невырожденным.
Если число заполненных клеток меньше
этого значения, то план (решение)
называется вырожденным. В случае
вырожденности плана условно считают одну
(или несколько) из пустых клеток занятой,
записывая в нее нулевую перевозку так,
чтобы число занятых клеток стало равным
m + n – 1.

34.

В нашей задаче число заполненных
клеток равно m + n – 1=3 + 4 – 1 = 6,
а пустых клеток – m × n – (m + n – 1), где
m – количество пунктов отправления,
n – количество пунктов назначения, что
в нашем случае 3 × 4 – 6 = 6.
Значит, найденный план является
невырожденным.

35. Метод потенциалов проверки решения на оптимальность

Предположим, что каждый пункт
отправления Ai вносит за перевозку
единицы груза какую-то сумму a i , а
каждый пункт назначения вносит
сумму b j . Эти платежи передаются
некоторому третьему лицу, например,
перевозчику. Величины a i и b jсвяжем
a i + b, где
равенствами
j = cij –
cij для базисных клеток.
тарифы

36.

Совокупность уравнений a i + b j = cij ,
составленных для всех базисных
переменных, представляет совместную
систему линейных уравнений, причем
одну из переменных можно задавать
произвольно и тогда остальные
переменные из системы уравнений
находятся однозначно.

37.

Обозначим через a i + b j = c ij , где c ij
назовем псевдостоимостями или косвенными
стоимостями (тарифами). Псевдостоимости
находятся для всех свободных клеток.
Платежи a i и b j не обязательно должны
быть положительны, поскольку не исключено,
что «перевозчик» сам платит тому или иному
пункту какую-то премию за перевозку.

38. Теорема «о платежах».

ai
Для заданной совокупности платежей
и b jсуммарная косвенная стоимость
перевозок при любом допустимом плане
сохраняет одно и тоже значение
m
n
F = åå c ij xij =c - const.
i =1 j =1
В этой формуле с зависит только от
совокупности платежей и не зависит от того,
каким именно допустимым планом
пользуемся.

39. Теорема оптимальности.

Если для всех базисных клеток
a i + b j = cij = c ij
а для всех свободных клеток
a i + b j = cij < cij
,
то допустимый план является оптимальным и
никаким способом улучшен быть не может.

40. Пример

Найти опорное решение методом
минимальной стоимости
и проверить оптимальность решения
методом потенциалов.

41.

42.

43.

Находим потенциалы базисных клеток
a1 + b1 = c11 = 2,
a1 + b 2 = c12 = 3,
a1 + b3 = c13 = 1,
a 22 + b = c22 = 2.

44.

Положим a1 = 0 и решим систему.
Получим b1 = 2, b 2 = 3, a 2 = -1, b3 = 1.
Найдем псевдостоимости пустых клеток
c21 = a 2 + b1 = -1 + 2 = 1,
c23 = a 2 + b3 = -1 + 1 = 0.
c21 = 1 < c21 = 4, c23 = 0 < c23 = 5.
План перевозок оптимален
X min = (30,10, 20, 0,30, 0),
F min = 2 × 30 + 3 ×10 + 1 × 20 + 2 × 30 = 150.

45. Пример 2.

На складах имеются запасы продукции
90, 400 и 110 тонн соответственно.
Потребители должны получить эту
продукцию в количествах 140, 300 и 160
тонн соответственно. Найти такой план
закрепления поставщиков к
потребителям, при котором суммы
затрат на перевозки минимальны.

46.

Расходы на перевозки 1 т продукции
заданы матрицей (у.е.)
æ 2 5 2ö
ç
÷
C = ç 4 1 5÷
ç3 6 8÷
è
ø
Сумма потребностей и сумма запасов
равны 140+300+160=90+400+110=600.
Модель закрытая.

47.

48.

План
0 ö
æ 90 0
ç
÷
X = ç 0 300 100 ÷
ç 50 0
÷
60
è
ø
Fmin = 2 × 90 + 1× 300 + 5 ×100 + 3 × 50 + 8 × 60 = 1600 y.e.

49.

2)Проверим план на оптимальность
методом потенциалов.
В таблице занято клеток
m + n -1 = 3 + 3 -1 = 5
Для них найдем потенциалы.

50.

a1 + b1 = 2,
a 2 + b 2 = 1,
a 2 + b 3 = 5,
a 3 + b1 = 3,
a 3 + b 3 = 8.
Положим a1 = 0.
Решим систему:
b1 = 2, a 3 = 1, b3 = 7, a 2 = -2, b 2 = 3.

51. Внесем в таблицу потенциалы занятых клеток

52.

Найдем оценки свободных клеток.
c12 = a1 + b 2 = 3,
g 12 = c12 - c12 = 5 - 3 = 2 > 0,
c13 = a1 + b3 = 7,
g 13 = c13 - c13 = 2 - 7 = -5 < 0,
c21 = a 2 + b1 = -2 + 2 = 0,
uur
c32 = a 3 + b 2 = 1 + 3 = 4.
g 21 = c21 - c21 = 4 - 0 = 4 > 0,
g 32 = c32 - c32 = 6 - 4 = 2 > 0.
Решение не оптимально, т.к. имеется
отрицательная оценка.

53.

3)Переход к другому решению.
Перераспределим грузы, перемещая их из
занятых клеток в свободные. Свободная
клетка становится занятой, а занятаясвободной.
Для свободной клетки с отрицательной
оценкой строится цикл(цепь, многоугольник),
все вершины которого, кроме одной
находятся в занятых клетках. Углы прямые,
число вершин четное

54.

Около свободной клетки цикла ставится (+), а
затем поочередно(-) , (+).У вершин со знаком
(-) выбирают минимальный груз, его
прибавляют к грузам, стоящим у вершин со
знаком (+) и отнимают от грузов у вершин со
знаком (-). В результате перемещения
получают новый опорный план. Это решение
проверяют на оптимальность и т. д. до тех
пор ,пока не получится оптимальное
решение.

55.

56.

57.

58.

Получили новое решение
0
60 ö
æ 30
ç
÷
X = ç 0 300 100 ÷ .
ç110 0
÷
0
è
ø
Проверим его на оптимальность,
вычислив потенциалы базисных клеток.

59.

Потенциалы заполненных клеток
a1 + b1 = 2,
a 2 + b 2 = 1,
a 3 + b1 = 3,
a1 + b3 = 2,
a 2 + b 3 = 5.
a1 = 0.
b1 = 2, a 3 = 1, b3 = 2, a 2 = 3, b 2 = -2.

60.

Оценки свободных клеток
c12 = a1 + b 2 = 0 - 2 = -2,
g 12 = c12 - c12 = 5 - (-2) = 7 > 0,
c21 = a 2 + b1 = 3 + 2 = 5,
g 21 = c21 - c21 = 4 - 5 = -1 < 0,
c32 = a 3 + b 2 = 1 - 2 = -1,
uur
c33 = a 3 + b 3 = 1 + 2 = 3.
g 32 = c32 - c32 = 6 - (-1) = 7 > 0,
g 33 = c33 - c33 = 8 - 3 = 5 > 0.
План не оптимален, т.к. оценка клетки
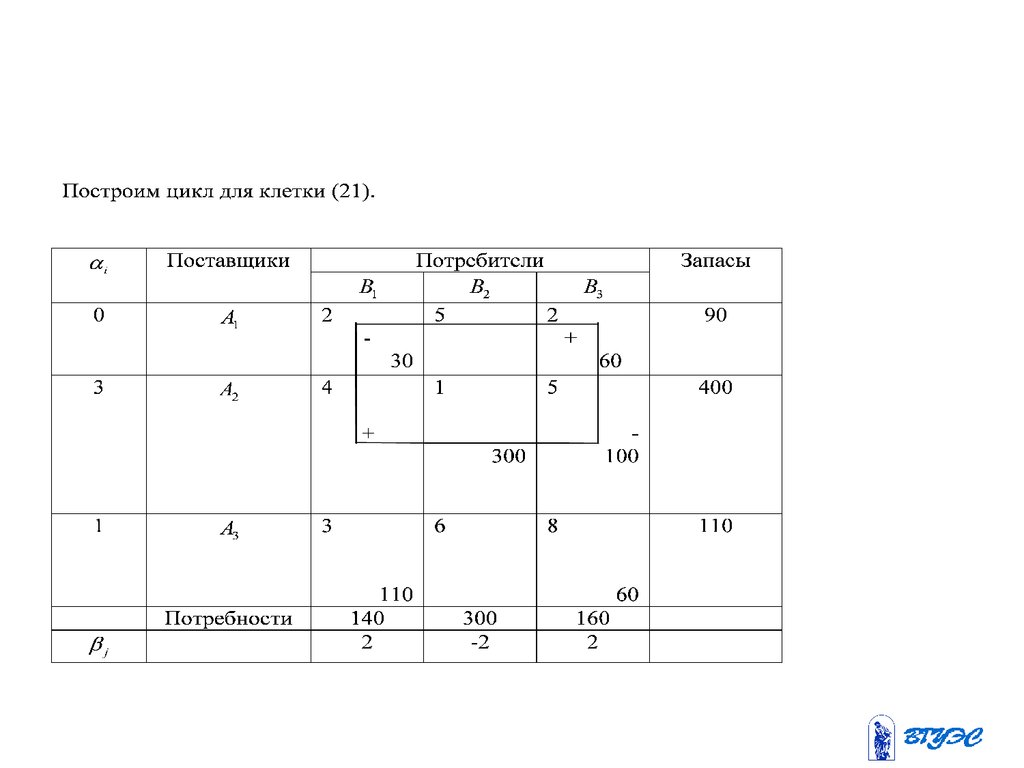
(21) отрицательна.

61.

62.

63.

0 90 ö
æ 0
ç
÷
X = ç 30 300 70 ÷
ç110 0
÷
0
è
ø
Новый план
Снова проверяем его на
оптимальность. Для занятых клеток
a + b = 2,
Находим
1
3
a 2 + b1 = 4,
a 2 + b 2 = 1,
a 2 + b 3 = 5,
a 3 + b1 = 3.
a1 = 0.
b3 = 2, a 2 = 3, b 2 = -2, a 3 = 2, b1 = 1.

64.

Для свободных клеток псевдостоимости
равны
c11 = a1 + b1 = 0 + 1 = 1,
c12 = a1 + b 2 = 0 - 2 = -2,
c32 = a 3 + b 2 = 2 - 2 = 0,
uur
c33 = a 3 + b3 = 2 + 2 = 4.

65.

Оценки свободных клеток
g 11 = c11 - c11 = 2 - 1 = 1 > 0,
g 12 = c12 - c12 = 5 - (-2) = 7 > 0,
g 32 = c32 - c32 = 6 - 0 = 6 > 0,
g 33 = c33 - c33 = 8 - 4 = 4 > 0.

66.

Все оценки положительны, поэтому план
оптимален.
0 90 ö
æ 0
Ответ:
ç
÷
X = ç 30 300 70 ÷
.
При этом
ç110
è
0
0 ÷ø
Font = 90 × 2 + 30 × 4 + 300 ×1 + 70 × 5 + 110 × 3 = 1280.
По сравнению с первоначальным планом
расходы уменьшились на величину
1610-1280=330у.е.