Полином Жегалкина

1.

2.

Теорема.
Любая функция алгебры логики
от n переменных может быть
представлена полиномом
Жегалкина и это представление
единственно.

3.

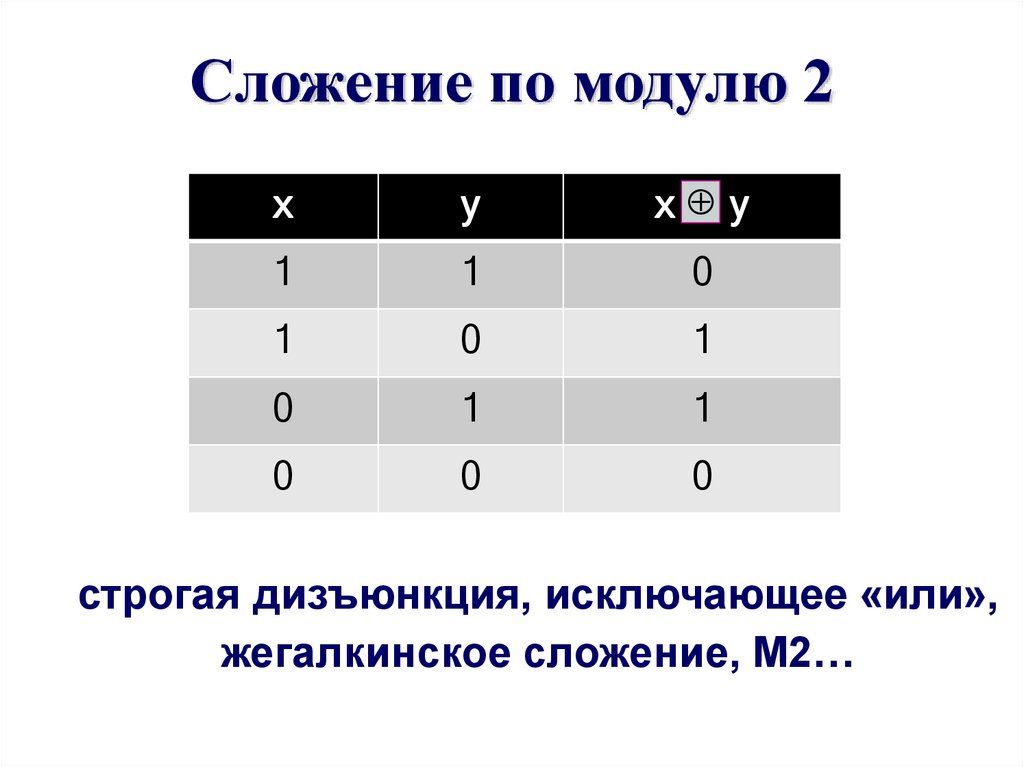
Сложение по модулю 2
x
y
y
xꚛ
1
1
0
1
0
1
0
1
1
0
0
0
строгая дизъюнкция, исключающее «или»,
жегалкинское сложение, M2…

4.

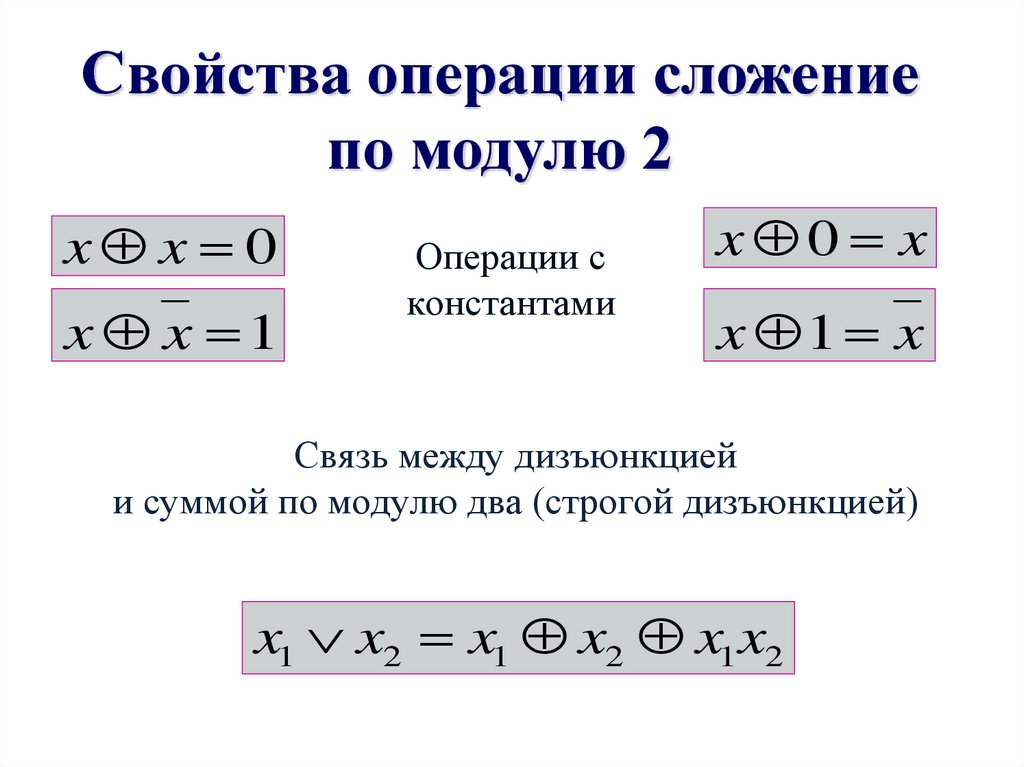
Свойства операции сложение
по модулю 2
x1 x2 x2 x1
x1 ( x2 x3 ) ( x1 x2 ) x3
x1 ( x2 x3 ) x1 x2 x1 x3
Возможно разложение в СДНФ
(освобождение от М2 или строгой дизъюнкции)
x1 x2 x1 x2 x1 x2

5.

Свойства операции сложение
по модулю 2
x x 0
x x 1
Операции с
константами
x 0 x
x 1 x
Связь между дизъюнкцией
и суммой по модулю два (строгой дизъюнкцией)
x1 x2 x1 x2 x1 x2

6.

Полином (многочлен) Жегалкина:
функция от 2 логических переменных
P x, y a0 a1 x a2 y a12 xy
функция от 3 логических переменных
P x, y, z a0 a1 x a2 y a3 z
a12 xy a13 xz a23 yz a123 xyz
a0 , a1 ,..., a123
- полиномиальные
коэффициенты (принимают
значение равное 0 или 1)

7.

Полином (многочлен) Жегалкина от n
логических переменных:
P x1 x2 x3 ...xn a0 a1 x1 a2 x2 ... an xn
a12 x1 x2 ... a123 x1 x2 x3 ... a123... n x1 x2 x3 ...xn
Всего здесь 2ⁿ слагаемых.
ꚛ - означает сложение по модулю 2,
Все полиномиальные коэффициенты являются
константами (равными нулю или единице).

8.

Алгоритм построения ПЖ
(с помощью эквивалентных преобразований)
1. Минимизируем булеву функцию любым
известным нам способом
2. Заменяем дизъюнкцию суммой по модулю 2
f1 f 2 f1 f 2 f1 f 2
3. Заменяем
xi xi 1
4. Используем распределительный закон
(раскрываем скобки)
5. Применяем
и
f f 0
f 0 f

9.

Метод неопределенных коэффициентов
(по таблице истинности или вектору значений функции)
x y z f a a x a y a z a xy a xz a yz a
0
1
2
3
12
13
23
123
xyz
0001 a
0011 a a 1 a
0100 a a 1 a
0110 a a a a 1 1 0 a
1001 a a 1 a
1010 a a a a 1 0 0 a
1101 a a a a 1 0 1 a
1111 a a a a a a a a 1 0 1 0 1 1 0 a
0
0
a
a0 1
0
3
3
a3 0
0
2
2
a2 1
0
2
0
1
0
1
3
13
13
a13 1
0
1
2
12
12
a12 1
1
3
23
23
1
2
3
12
13
23
123
123
P 1 y x y x z x yz
a23 0
a1 0
a123 1

10.

А теперь самостоятельно потрудимся
над получением полинома Жегалкина
в тетрадях.

11.

Иван Иванович Жегалкин (1869-1947) – российский и
советский математик и логик, профессор Московского
университета. Заслуженный деятель науки РСФСР один из
основоположников современной математической логики. Из его
открытий наибольшую известность получил так называемый
полином Жегалкина. Жегалкин награжден Орденом Трудового
Красного Знамени.
Жегалкин предложил в 1927 году в качестве
удобного средства для представления функций булевой логики многочлен, названный
полиномом Жегалкина.
Известный советский математик Николай
Лузин, вспоминая студенческие годы,
говорит, что из профессоров не боялся лишь
Жегалкина.

12.

Вариант А
x ∧ (y →z)
xyz f
0000 a
0010 0 a
0100 0 a2
0110 0 0 0 a
1001 0 a1
1011 0 1 0 a
1100 0 1 0 a12
1111 0 1 0 0 1 0 0 a
0
3
23
13
123
P x x y x yz
a
a0 0
a3 0
a2 0
a23 0
a1 1
a13 0
a12 1
a123 1

13.

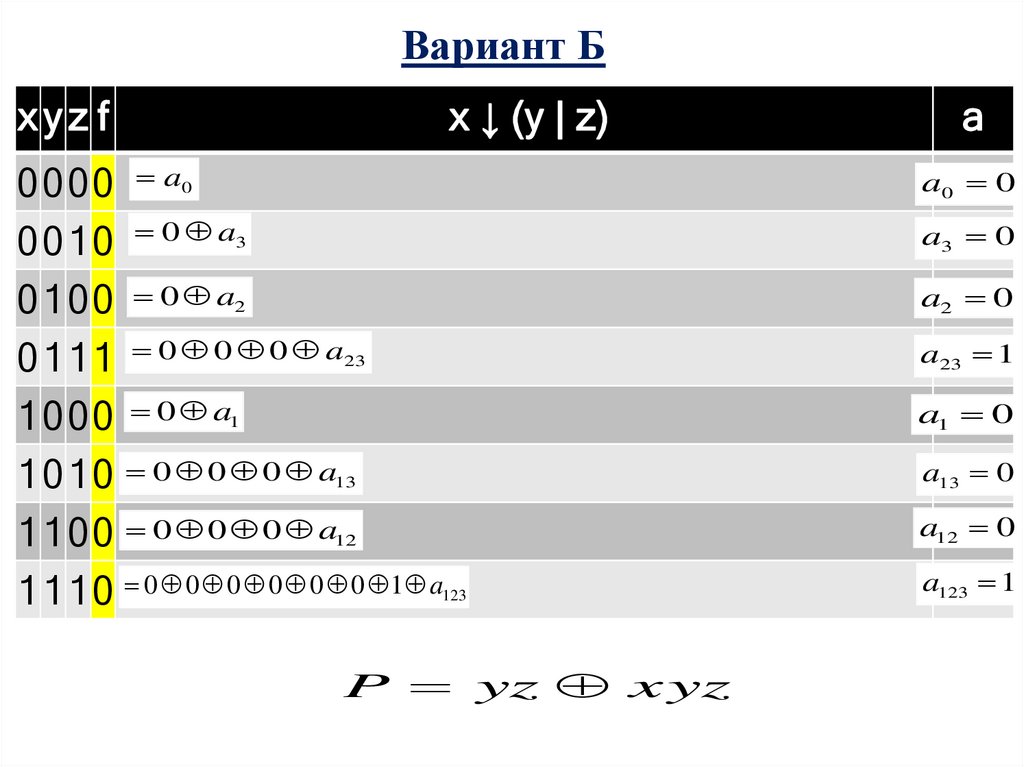
Вариант Б
xyz f
x ↓ (y | z)
0000 a
0010 0 a
0100 0 a2
0111 0 0 0 a
1000 0 a1
1010 0 0 0 a
1100 0 0 0 a12
1110 0 0 0 0 0 0 1 a
0
3
23
13
123
P yz x yz
a
a0 0
a3 0
a2 0
a23 1
a1 0
a13 0
a12 0
a123 1

14.

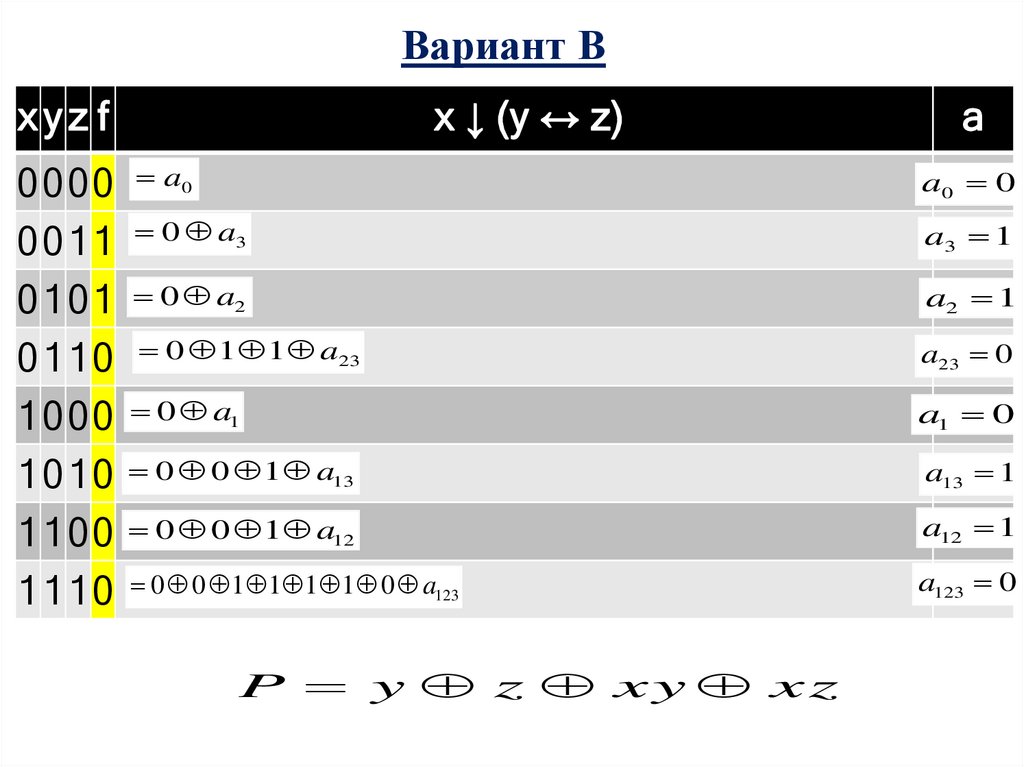
Вариант В
xyz f
x ↓ (y ↔ z)
0000 a
0011 0 a
0101 0 a2
0110 0 1 1 a
1000 0 a1
1010 0 0 1 a
1100 0 0 1 a12
1110 0 0 1 1 1 1 0 a
0
3
23
13
123
P y z xy xz
a
a0 0
a3 1
a2 1
a23 0
a1 0
a13 1
a12 1
a123 0

15.

Вариант Г
x ∨ (y ↔ z)
xyz f
0001 a
0010 1 a
0100 1 a2
0111 1 1 1 a
1001 1 a1
1011 1 0 1 a
1101 1 0 1 a12
1111 1 0 1 1 1 1 0 a
0
3
23
13
123
P 1 y z xy xz
a
a0 1
a3 1
a2 1
a23 0
a1 0
a13 1
a12 1
a123 0

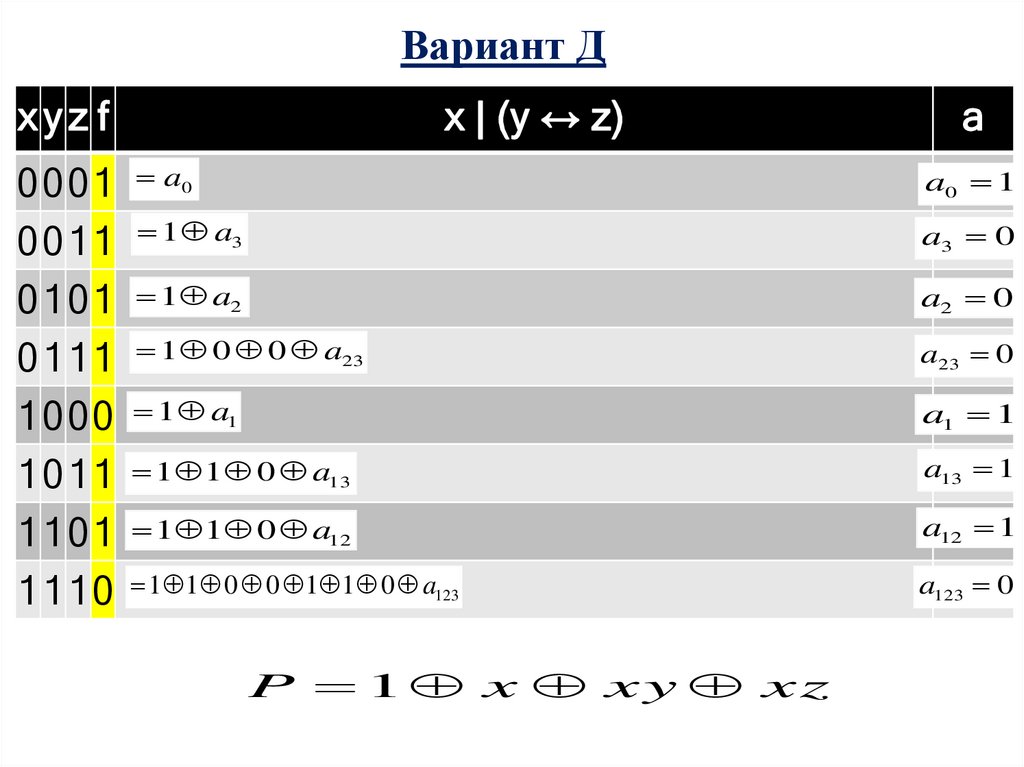
16.

Вариант Д
xyz f
x | (y ↔ z)
0001 a
0011 1 a
0101 1 a2
0111 1 0 0 a
1000 1 a1
1011 1 1 0 a
1101 1 1 0 a12
1110 1 1 0 0 1 1 0 a
0
3
23
13
123
P 1 x xy xz
a
a0 1
a3 0
a2 0
a23 0
a1 1
a13 1
a12 1
a123 0

17.

Дополнительное задание.
Пусть функция задана вектором значений
f = (11001011).
Найти полином Жегалкина.

18.

ОЖИДАЕМЫЕ
РЕЗУЛЬТАТЫ:
ВАШ ВАРИАНТ
ОТВЕТ
Вариант А
Вариант Б
Вариант В
Вариант Г
Вариант Д