Похожие презентации:
Математическая логика и теория алгоритмов. Булевы функции
1. Математическая логика и теория алгоритмов
Доцент каф. АОИ, к.т.н. Перемитина Татьяна ОлеговнаМатематическая логика
и теория алгоритмов
Булевы функции
2. Булевы функции
Введение в булеву алгебру.Способы задания булевых
функций.
Минимизация булевых функций.
Представление булевых функций
полиномами Жегалкина.
2
3. Булева алгебра
х {0,1} f ( х) : {0,1} {0,1}Способы задания булевых
функций:
• Табличный;
• Графический;
• Аналитический.
Вопрос: Сколько существует различных
булевых функций от одной переменной?
3
4.
Табличное заданиебулевых функций
Count f ( x1 ,..., xn ) 2
2
f ( х), n 1, Count f ( x) 2 4
f 2 ( x) f 3 ( x )
f1 ( x)
f 0 ( x)
2n
1
Вопрос: Сколько существует различных
булевых функций от двух переменных?
4
5.
Табличное заданиебулевых функций
f : {0,1} {0,1} {0,1}
f0
f1
f2
– «тождественный нуль»;
– конъюнкция;
– отрицание импликации;
5
6.
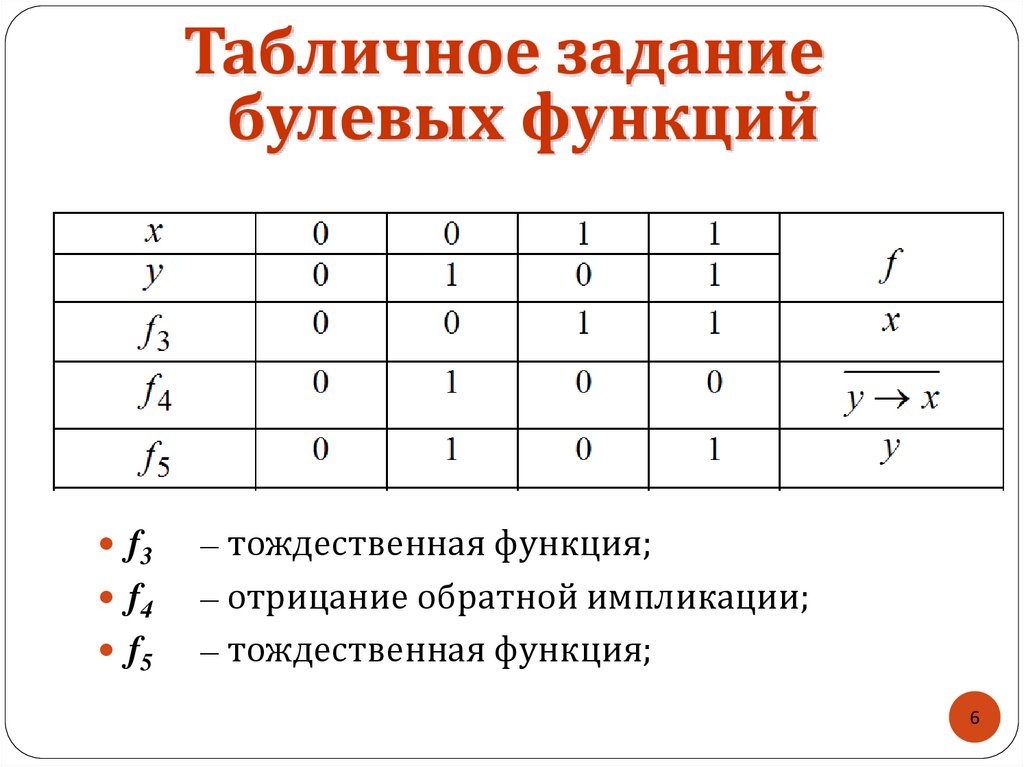
Табличное заданиебулевых функций
f3
f4
f5
– тождественная функция;
– отрицание обратной импликации;
– тождественная функция;
6
7.
Табличное заданиебулевых функций
f6
f7
f8
– сумма по модулю 2 (сумма Жегалкина);
– дизъюнкция;
– стрелка Пирса;
7
8.
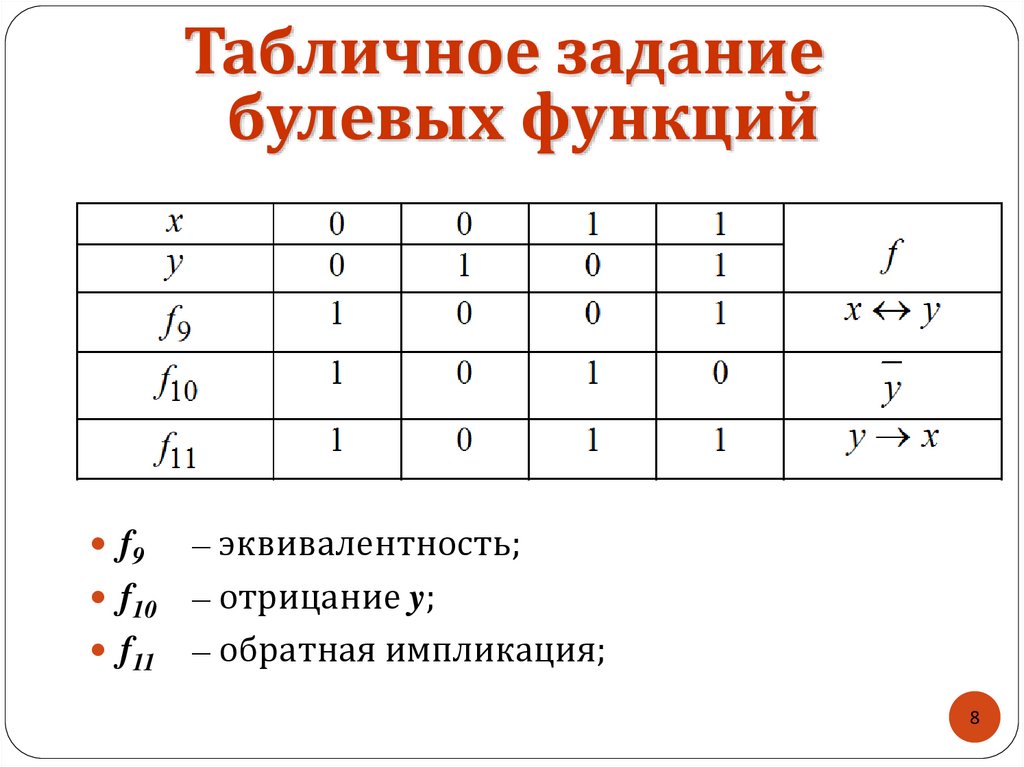
Табличное заданиебулевых функций
f9
f10
f11
– эквивалентность;
– отрицание y;
– обратная импликация;
8
9.
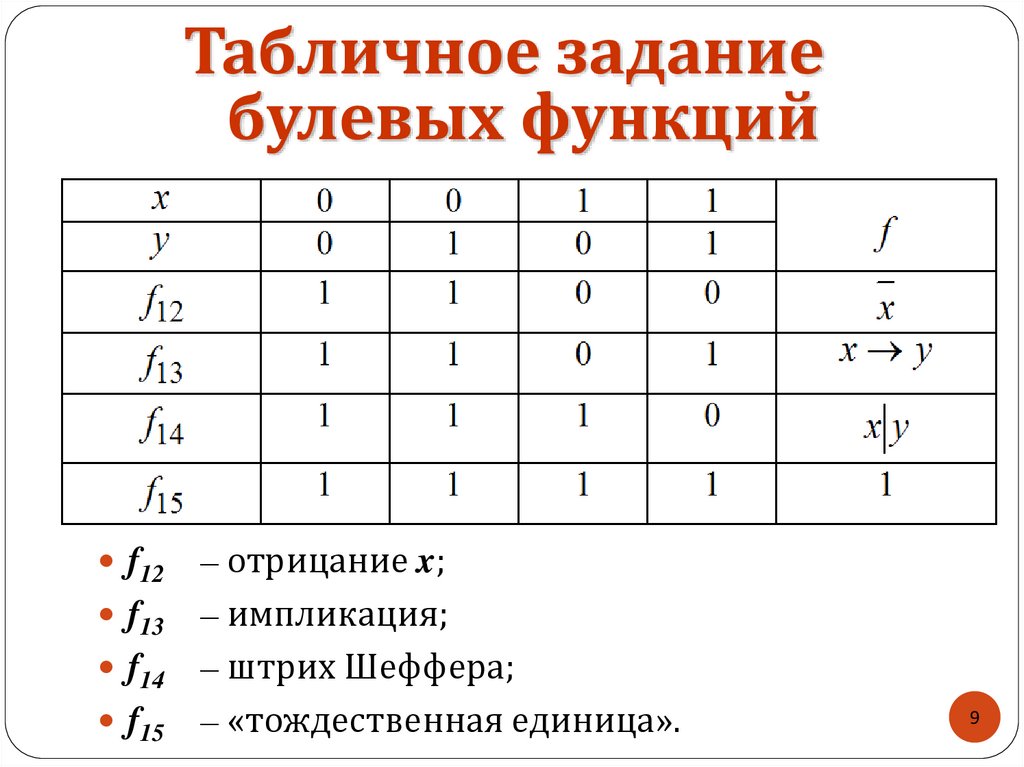
Табличное заданиебулевых функций
f12
f13
f14
f15
– отрицание x;
– импликация;
– штрих Шеффера;
– «тождественная единица».
9
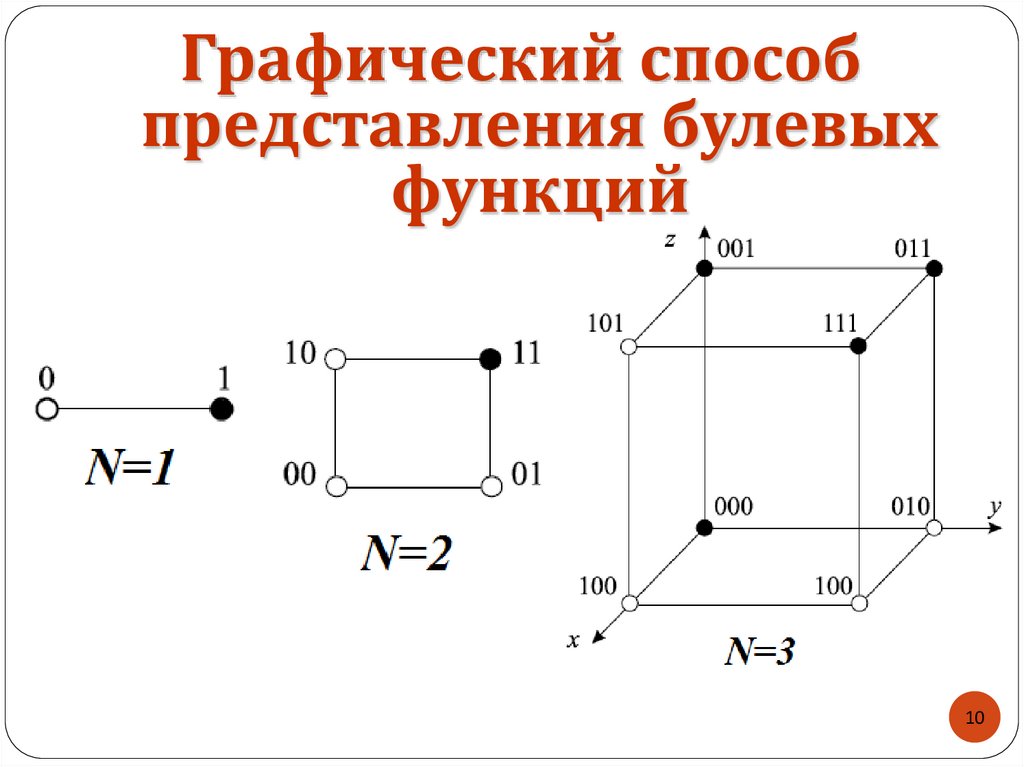
10. Графический способ представления булевых функций
1011. Пример 1
Укажите булеву функцию,графическое представление
которой имеет следующий вид:
Из графического представление определяем, что
f (0) 1; f (1) 0.
Ответ: графически представлена f ( x) х
11
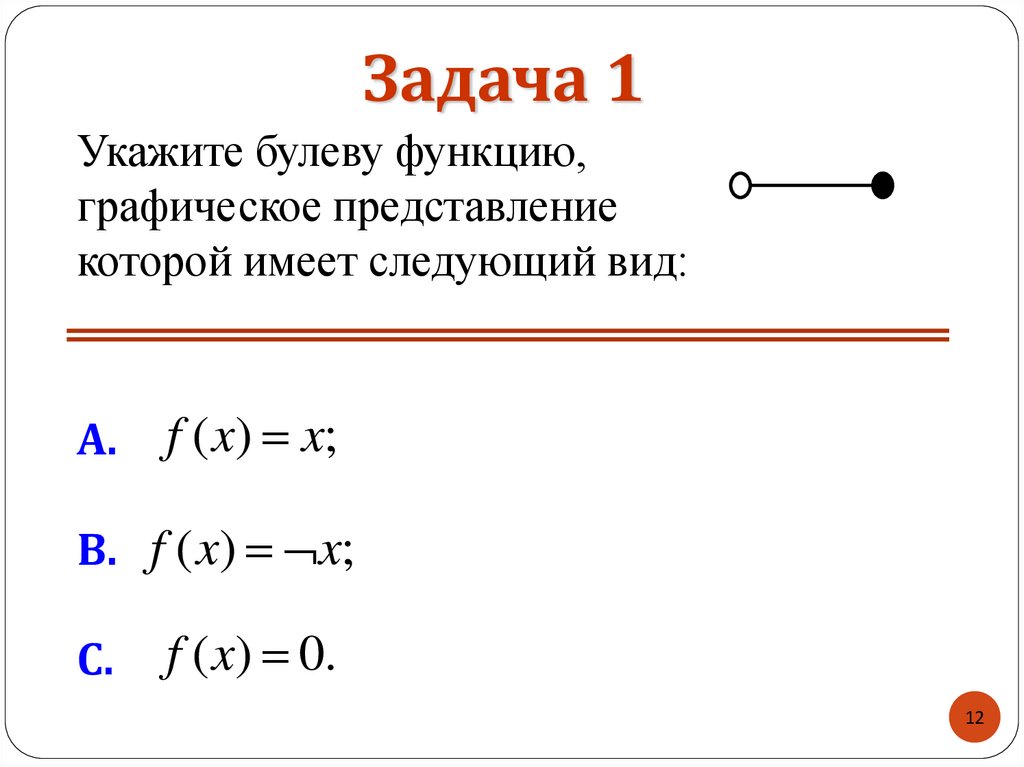
12. Задача 1
Укажите булеву функцию,графическое представление
которой имеет следующий вид:
A.
f ( x) x;
B. f ( x) x;
C.
f ( x) 0.
12
13. Пример 2
Укажите булеву функцию,графическое представление
которой имеет следующий вид:
Из графического представления
определяем, что
f (0,0) 0; f (0,1) 0;
f (1,0) 1; f (1,1) 1 .
Ответ:
Графически представлена
f ( x, y) x.
13
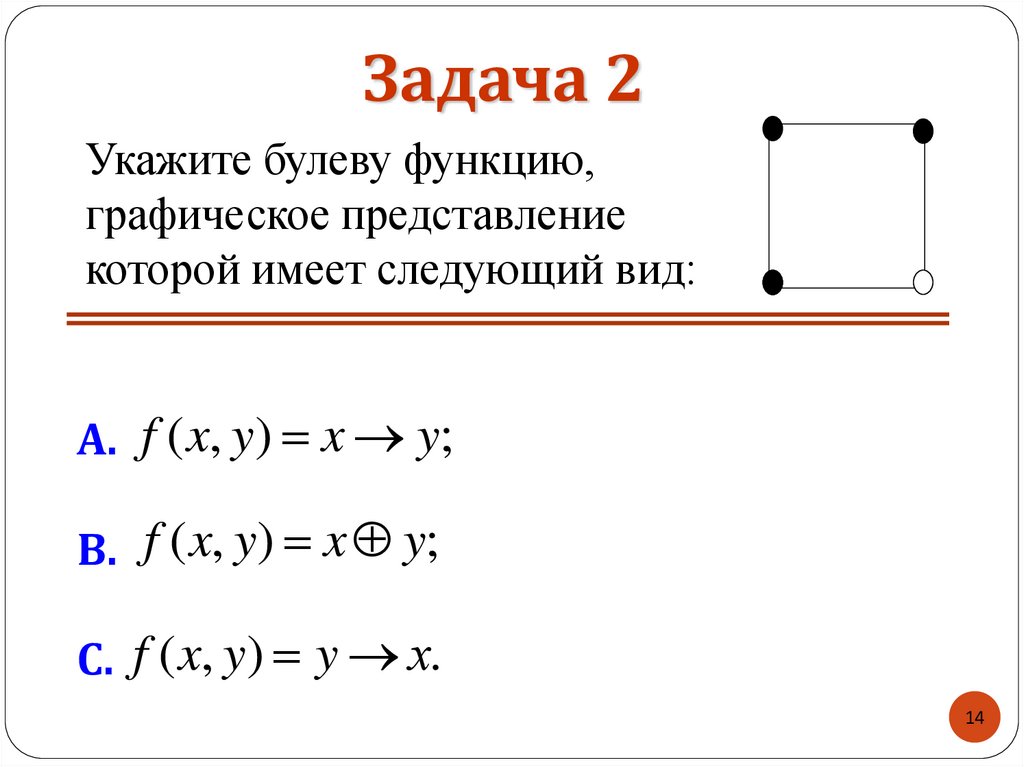
14. Задача 2
Укажите булеву функцию,графическое представление
которой имеет следующий вид:
A. f ( x, y) x y;
B. f ( x, y) x y;
C. f ( x, y) y х.
14
15.
Существенные ификтивные переменные
Булева функция f(x1, … xi,….,xn)
существенно зависит от переменной xi ,
если существует такой набор значений
переменных , что:
f(x1, … 0,….,xn)≠ f(x1, … 1,….,xn) .
Пример 3:
Какая переменная является существенной?
f ( x, y ) x ( x y )
15
16.
Решениеf ( x, y ) x ( x y )
f (0, y ) 0 (0 y ) 0;
f (1, y ) 1 (1 y ) 1; f (0, y ) f (1, y )
x существенная переменная.
f ( x,0) x ( x 0) x;
f ( x,1) x ( x 1) x; f ( x,0) f ( x,1)
y фиктивная переменная.
16
17. Задача 3
Для какой функции переменная х являетсясущественной?
A. f ( x, y) x y;
B. f ( x, y) x х у;
C. f ( x, y) ( x y) ( х у).
17
18. Решение
A. f ( x, y) x y х у11
f (0, y) 1 у 1; f (1, y) 0 у у;
х существенн ая переменная
B. f ( x, y) x х у 1 все переменные
фиктивные.
C. f ( x, y) ( x y) ( х у) у значит
10
переменная х фиктивная.
18
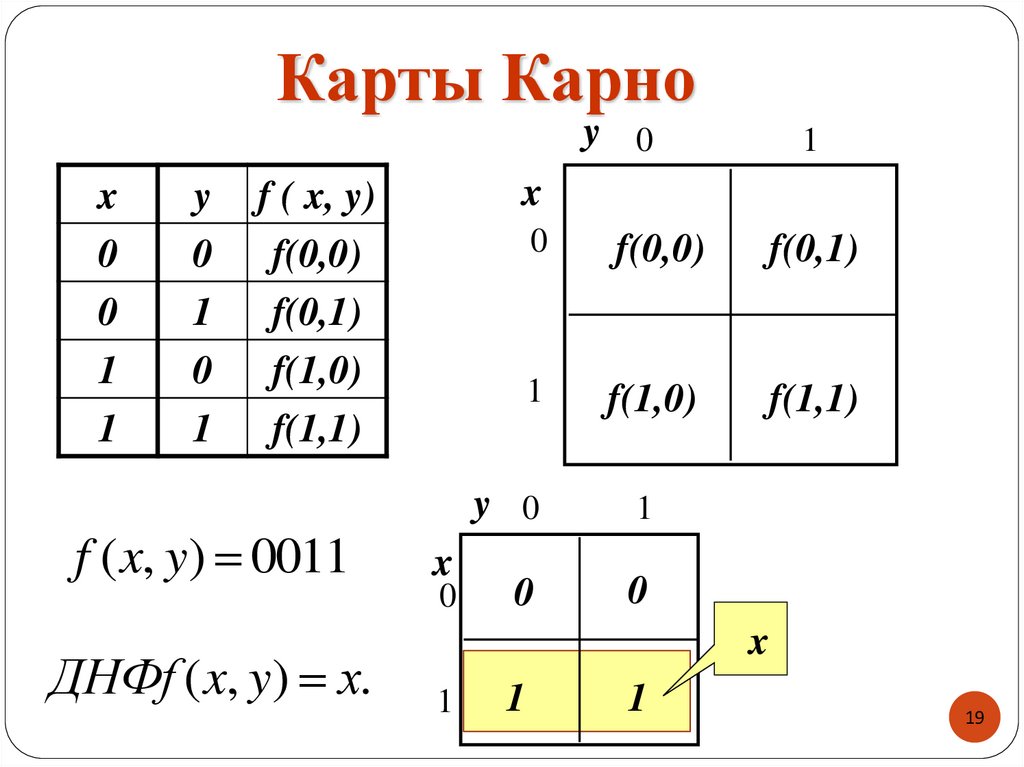
19. Карты Карно
y 0x
0
0
1
1
y
0
1
0
1
x
f ( x, y)
f(0,0)
f(0,1)
f(1,0)
f(1,1)
f ( x, y) 0011
x
0
ДНФf ( x, y) х.
1
0
f(0,0)
f(0,1)
1
f(1,0)
f(1,1)
y 0
1
0
0
x
1
1
1
19
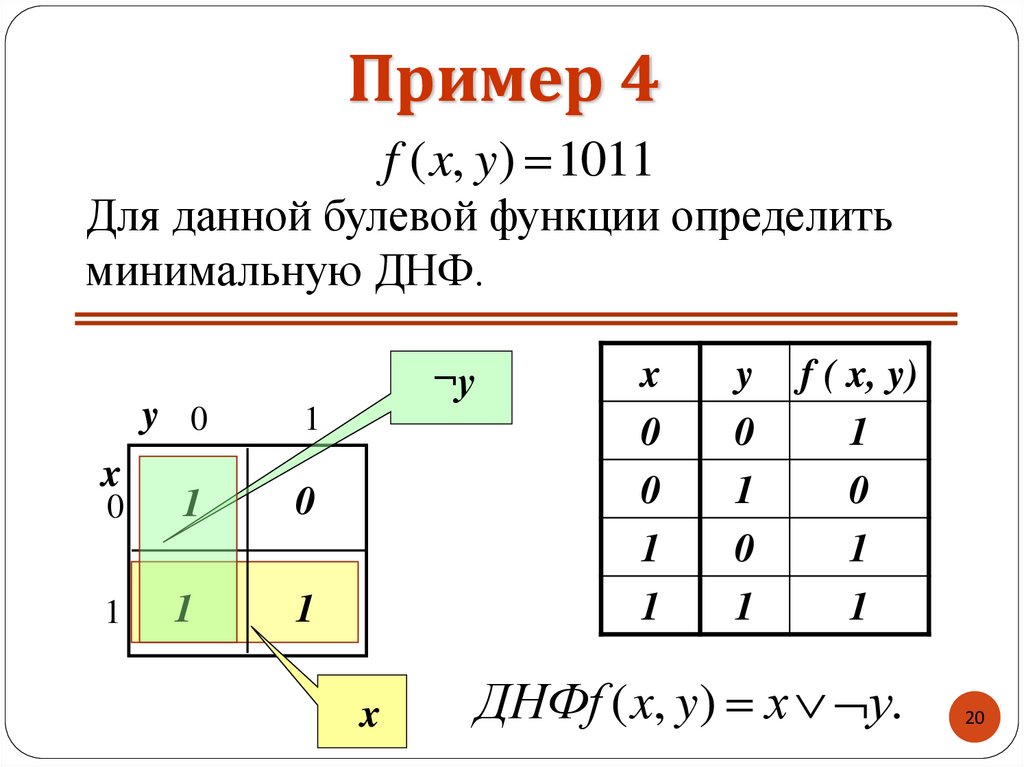
20. Пример 4
f ( x, y) 1011Для данной булевой функции определить
минимальную ДНФ.
¬у
y 0
1
0
1
0
1
1
1
x
x
x
0
0
1
1
y
0
1
0
1
f ( x, y)
1
0
1
1
ДНФf ( x, y) х у.
20
21. Задача 4
f ( x, y) 1100Для данной булевой функции определить
минимальную ДНФ:
A.
f ( x, y) х у;
B.
f ( x, y) х;
C.
f ( x, y) у.
21
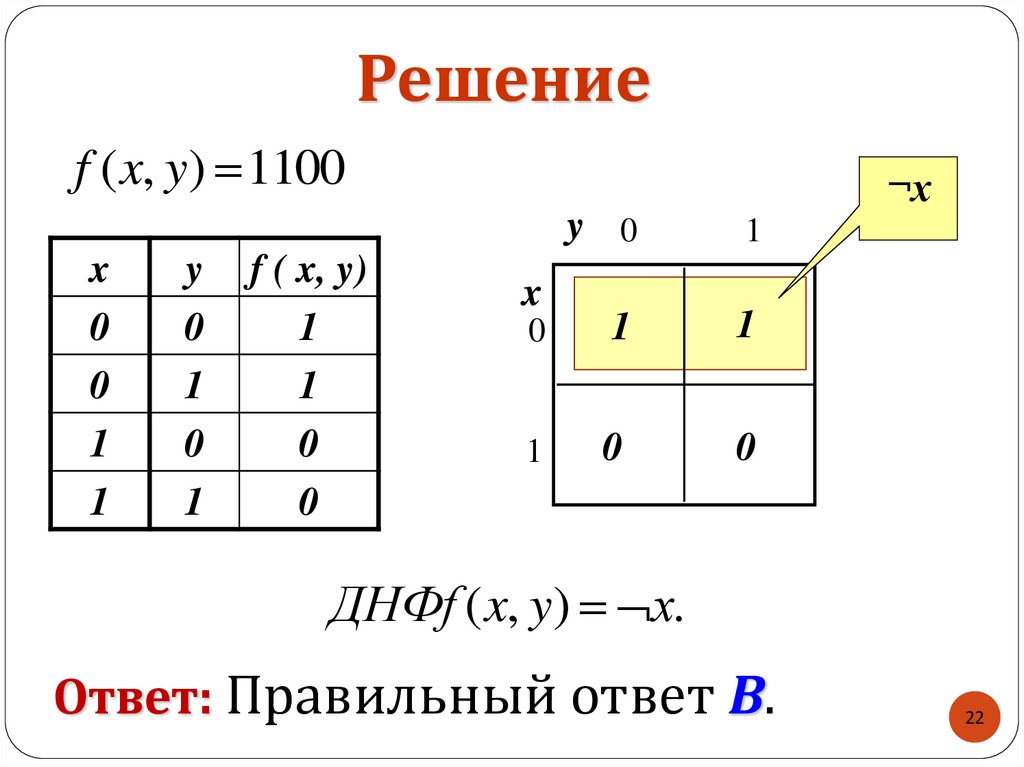
22. Решение
f ( x, y) 1100x
0
0
1
1
y
0
1
0
1
f ( x, y)
1
1
0
0
¬х
y 0
1
0
1
1
1
0
0
x
ДНФf ( x, y) х.
Ответ: Правильный ответ В.
22
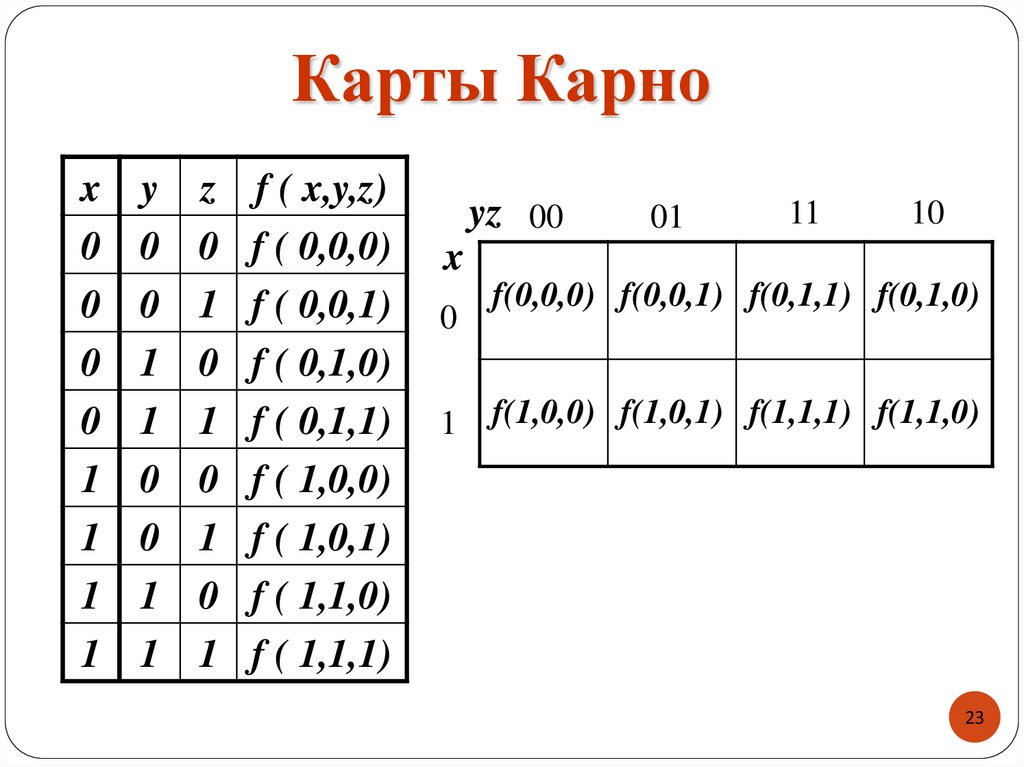
23. Карты Карно
x0
0
0
0
1
1
1
1
y
0
0
1
1
0
0
1
1
z
0
1
0
1
0
1
0
1
f ( x,y,z)
f ( 0,0,0)
f ( 0,0,1)
f ( 0,1,0)
f ( 0,1,1)
f ( 1,0,0)
f ( 1,0,1)
f ( 1,1,0)
f ( 1,1,1)
yz 00
01
11
10
x
0
1
f(0,0,0) f(0,0,1) f(0,1,1) f(0,1,0)
f(1,0,0) f(1,0,1) f(1,1,1) f(1,1,0)
23
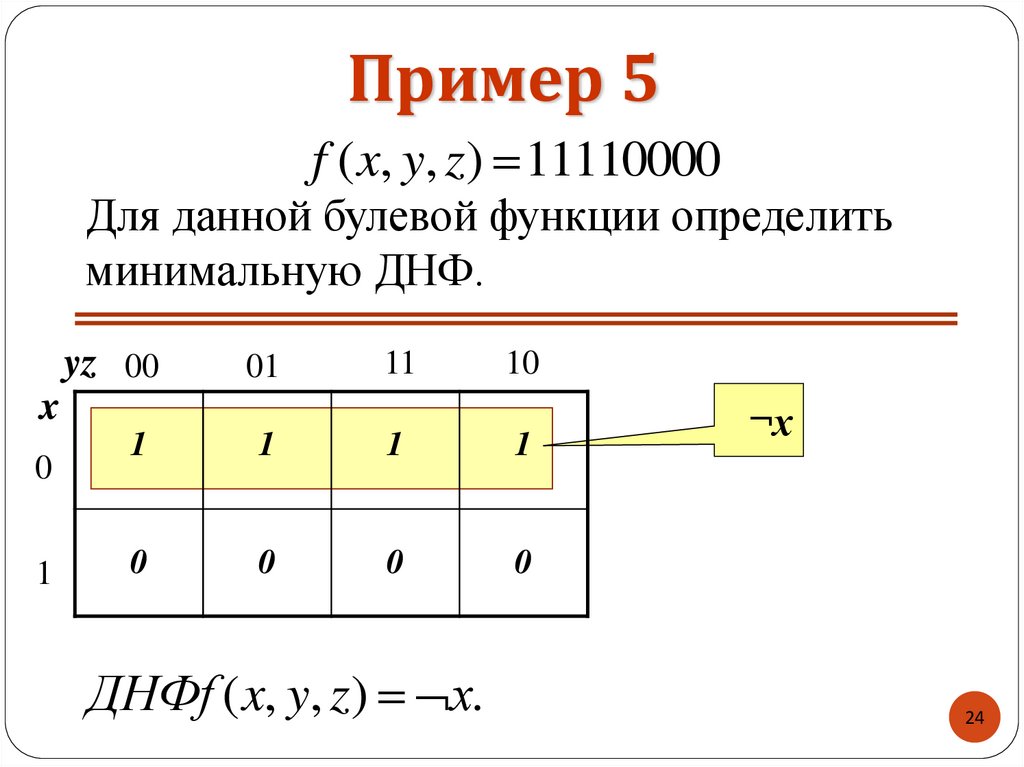
24. Пример 5
f ( x, y, z) 11110000Для данной булевой функции определить
минимальную ДНФ.
yz 00
01
11
10
x
0
1
1
1
1
1
0
0
0
0
ДНФf ( x, y, z) х.
¬x
24
25. Карты Карно
zw 0001
11
10
f(0,0,0,0)
f(0,0,0,1)
f(0,0,1,1)
f(0,0,1,0)
01
f(0,1,0,0)
f(0,1,0,1)
f(0,1,1,1)
f(0,1,1,0)
11
f(1,1,0,0)
f(1,1,0,1)
f(1,1,1,1)
f(1,1,1,0)
10
f(1,0,0,0)
f(1,0,0,1)
f(1,0,1,1)
f(1,0,1,0)
xy
00
25
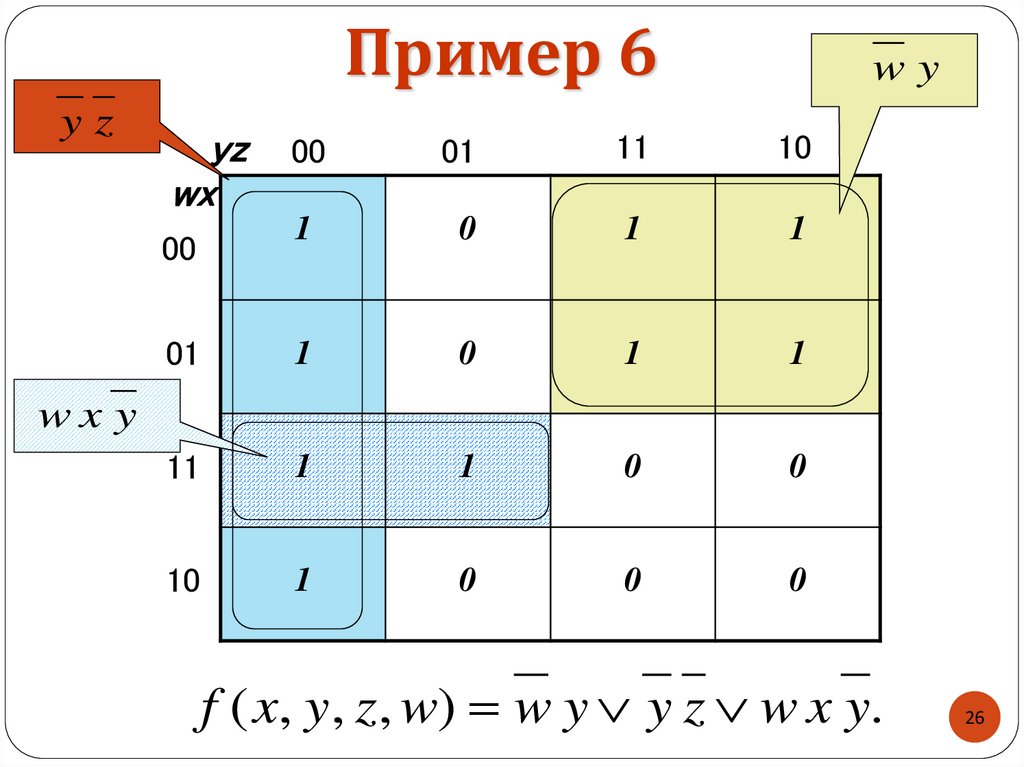
26.
Пример 6yz
wy
yz
wx
00
01
11
10
00
1
0
1
1
01
1
0
1
1
11
1
1
0
0
10
1
0
0
0
wx y
f ( x, y, z , w) w y y z w x y.
26
27. Алгебра Жегалкина
Закон коммутативности:x y y x
Закон дистрибутивности:
x y z xy xz
1
Законы ассоциативности:
x y z x y z
x y z x y z
x x 0; х 0 х; х 1 х.
27
28. Представление булевых функций полиномами Жегалкина
f x1 ,..., xn a0 a1 x1...an xna12 x1 x2 ... an 1,n xn 1 xn
a123 x1 x2 x3 ... a1... n x1 x2 ...xn ,
где a0 ,..., a1... n 0,1
28
29. Пример 7
f ( x, y) х уПредставьте данную булеву функцию в
виде полинома Жегалкина
f ( x, y) ( х y) (( x 1) ( y 1) 1)
(( х y x y 1) 1)
( х y x y) 1 1
х y x y.
Ответ: f ( x, y) х y x y.
29


















 Математика
Математика








