Похожие презентации:
Методы сетевого планирования и управления в задачах системного анализа
1.
Южный федеральный университетКафедра синергетики и процессов управления
Презентация к практическим занятиям по
дисциплине
«Теория систем и системный анализ»
тема:
«Методы сетевого планирования и
управления в задачах системного анализа»
2.
Список рекомендованной литературы:1.
Таха Хемди А. Введение в исследование операций. – М.: Вильямс, 2007.
2.
Гладких Б.А. Методы оптимизации и исследование операций для
бакалавров информатики. Ч. 4. Сетевое планирование и массовое
обслуживание: учебное пособие. – Томск: Изд-во НТЛ, 2013. – 164 с.
3.
http://www.youtube.com/playlist?list=PL3L1fFlpk8EBzvdeREAildlM9-CDg7tFX
4.
http://www.book.ru/book/918272
2
3.
1. Методы сетевого планирования и управленияВ современном индустриальном обществе с 1960–1970 гг. стали широко использоваться
научные методы оптимальной организации производства, которые были разработаны
для управления разработками сверхсложных технических систем (ракетно-космических
комплексов, уникальных строек и др.) и которые во второй половине XX века
сформировались в самостоятельную науку управление проектами (project
management). Эти же методы в настоящее время широко используются для оптимальной
организации проектов в IT-сфере.
Выполнение комплексных проектов зачастую требует календарной увязки большого
числа взаимосвязанных работ, выполняемых различными подразделениями
(организациями, отдельными людьми, командами разработчиков ПО и т.п.).
Как показала практика, наиболее эффективным способом упорядочения работ в сложном
проекте является сетевое планирование и управление (СПУ) [network-based
analysis, planning, scheduling], основанное на математическом аппарате теории графов,
математического программирования и теории вероятностей.
Особенностью таких проектов является то, что в них имеется большое число
элементарных работ, связанных условиями технологической зависимости
(предшествования), для их выполнения требуются разнообразные ресурсы (людские,
материальные, энергетические, финансовые), которые, как правило, ограничены.
Задача СПУ состоит в оптимальном календарном, ресурсном, стоимостном планировании
проектов и поддержки оперативного управления ими.
3
4.
Примеры проектов:разработка и изготовление сложного изделия (в том числе программного
обеспечения);
строительство;
единичное, крупное и мелкосерийное производство;
выполнение образовательной программы;
НИР / НИОКР / ОКР и др.
Наиболее известные методы из СПУ:
метод критического пути (Critical Path Method СРМ);
метод планирования и руководства программами разработок
(Program Evaluation and Review Technique PERT).
4
5.
1.1. Проект и его сетевая модельПод проектом (project) понимается некоторый комплекс взаимосвязанных работ
(activities, tasks) / процессов. Работа – это некоторое действие, приводящее к
достижению определенного результата.
Каждая работа имеет четко выраженные моменты начала и окончания и в общем
случае требует для своего выполнения: 1) время, 2) ресурсы.
С этой точки зрения работы могут быть классифицированы на три группы:
реальные работы, требующие времени и ресурсов, к ним относится
большинство работ в проекте;
работы-ожидания требуют времени, но не нуждаются в ресурсах (например,
ожидание высыхания краски или затвердения цемента, ожидание резолюции
начальника на документе и др.);
фиктивные работы (dummies) имеют нулевую продолжительность и не
требуют ресурсов (такие работы иногда необходимы для синхронизации других
работ или показывают взаимосвязь между работами).
Продолжительность или длительность (duration) является важнейшей
характеристикой работы. В сетевом планировании имеются два подхода:
1) с постоянными и известными заранее длительностями (производство по
известной технологии и др.);
2) со случайными длительностями работ (научное исследование,
программирование и др.).
5
6.
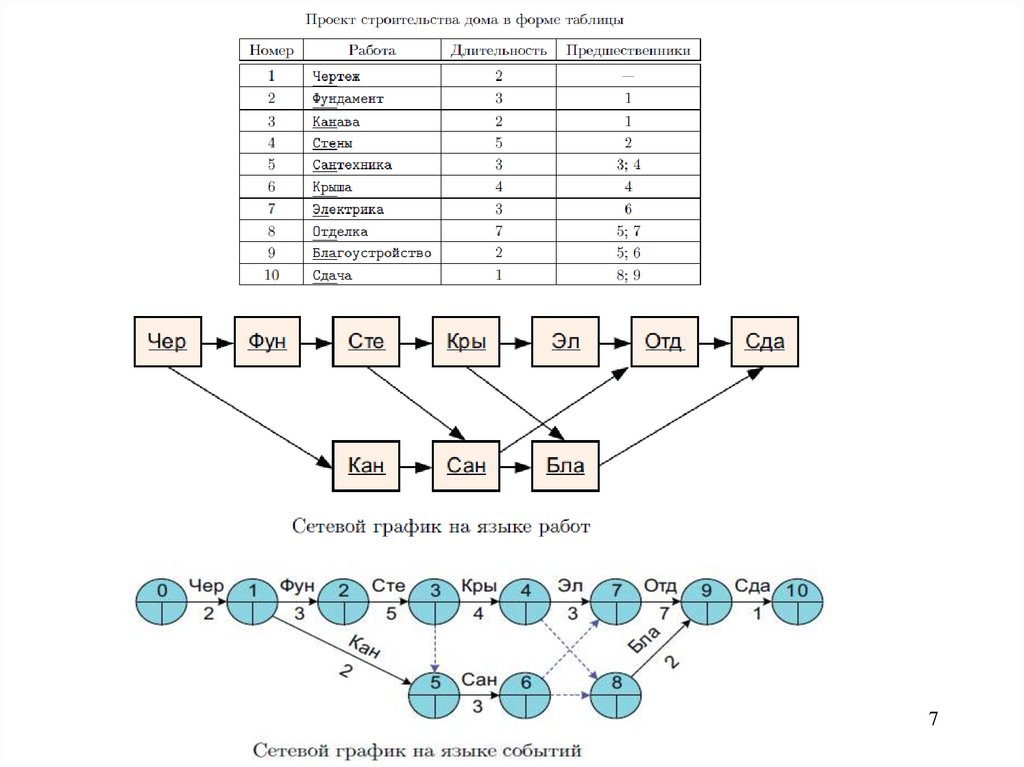
На рисунке выше показаны этапы применения методов СПУ.Планирование проекта всегда начинается с табличного представления, однако
работать с ним неудобно. Суть сетевого планирования и управления состоит в
графическом представлении проекта в виде сетевой модели (network chart, network
diagram, arrow diagram), и затем в виде временного графика – диаграммы Ганта.
Исходные данные для построения сетевой модели могут задаваться различными
способами:
описанием предполагаемого проекта. В этом случае необходимо
самостоятельно разбить его на отдельные работы и установить их взаимные связи;
списком работ проекта. В этом случае необходимо проанализировать
содержание работ и установить существующие между ними связи;
списком работ проекта с указанием их упорядочения. В этом случае
необходимо только отобразить работы на сетевом графике.
Изобразить сетевую модель можно двумя способами:
1) на языке работ (activity-on-node AON, или precedence diagramming method
PDM) и
2) на языке событий (activity-on arrow AOA, или arrow diagramming method ADM). 6
7.
78.
Сетевая модель AON представляет собой ориентированный граф, вершинамикоторого являются работы, а дуги отображают отношение предшествования:
стрелка направлена от предшествующей работы к последующей.
Последующая работа может быть начата только после того, как выполнены все
предшествующие ей работы.
Язык AON является самым естественным, однако алгоритмы вычислений в этом
случае получаются более сложными.
8
9.
Сетевая модель на языке событий представляет собой ориентированный граф,вершинами которого являются события (events), а дуги обозначают работы.
Событие – это момент времени, когда завершаются одни работы и начинаются
другие. Событие представляет собой результат проведенных работ и, в отличие от
работ, не имеет протяженности во времени. Любое событие может считаться
наступившим только тогда, когда закончатся все входящие в него работы. Поэтому
работы, выходящие из некоторого события, не могут начаться, пока не будут
завершены все работы, входящие в это событие.
Для визуального представления проекта на языке событий каждая вершина графа
изображается в виде круга, разделенного на три сектора. Верхний предназначен
для номера события (порядок нумерации рассмотрим далее), а два нижних
резервируем для ранних E(arly) и поздних L(ate) сроков его наступления.
Работа, соединяющая два события, обозначается стрелкой с двумя метками:
верхняя идентифицирует работу (необязательный, но удобный элемент, задающий
наименование работы), а нижняя указывает на ее продолжительность.
9
10.
При составлении сетевой модели AOA следует придерживаться следующих шестиправил:
1. В графе не должно быть орциклов (замкнутых контуров). Алгоритм выявления
орциклов приведен далее. Орциклы, если они есть, исправить невозможно,
следует пересмотреть сам проект.
2. В графе должна быть одна и только одна вершина, в которую не идет ни одна
дуга. Если таких вершин несколько, следует добавить вспомогательную вершину
начало проекта, и фиктивные работы с нулевой продолжительностью.
Фиктивные работы обычно изображаются штриховыми линиями.
3. В графе должна быть одна и только одна вершина, из которой не выходит ни
одна дуга. Если таких вершин несколько, следует добавить вспомогательную
вершину конец проекта, и фиктивные работы.
10
11.
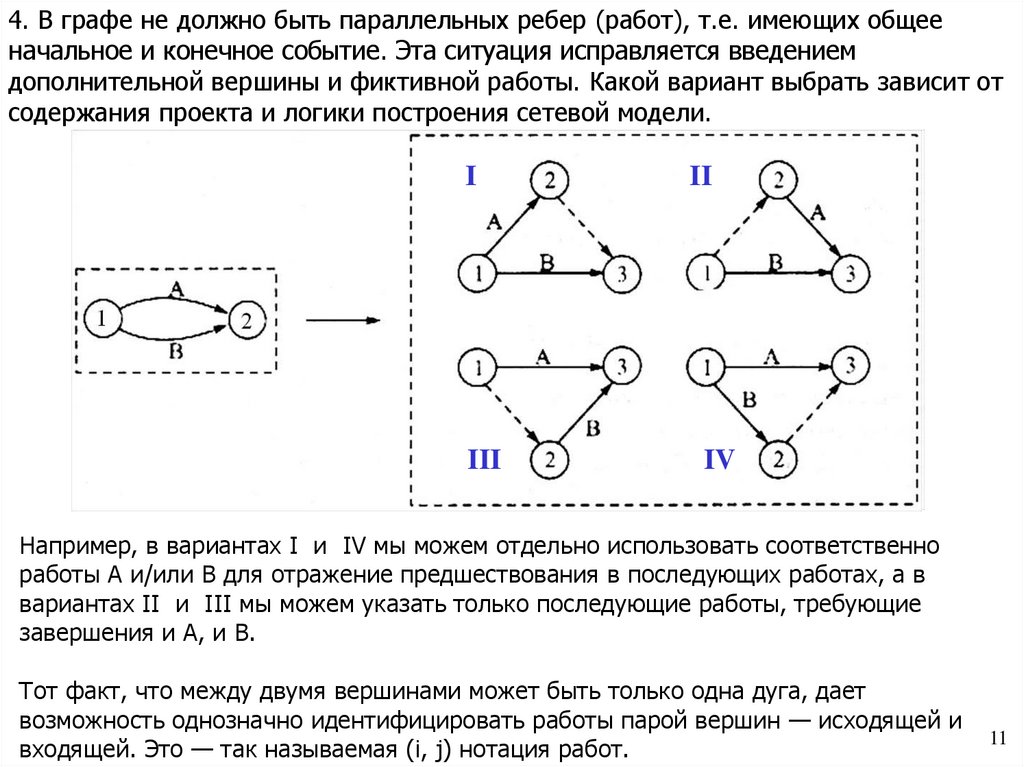
4. В графе не должно быть параллельных ребер (работ), т.е. имеющих общееначальное и конечное событие. Эта ситуация исправляется введением
дополнительной вершины и фиктивной работы. Какой вариант выбрать зависит от
содержания проекта и логики построения сетевой модели.
II
II
III
IV
Например, в вариантах I и IV мы можем отдельно использовать соответственно
работы А и/или В для отражение предшествования в последующих работах, а в
вариантах II и III мы можем указать только последующие работы, требующие
завершения и А, и В.
Тот факт, что между двумя вершинами может быть только одна дуга, дает
возможность однозначно идентифицировать работы парой вершин — исходящей и
входящей. Это — так называемая (i, j) нотация работ.
11
12.
5. Если для начала одной из последующих работ требуетсявыполнение не всей входящей работы, а только ее части, то входящую работу
следует разделить на две части и граф перестроить в соответствии с рисунком:
Пусть работа а означает покраску пола, работа b проветривание помещения, а работа c
расстановку мебели. Тогда работу а логично разделить на две части: a1 подсушивание
краски до состояния, когда можно пройти в комнату и открыть форточку,
и a2 окончательная просушка краски, т.е. а = a1 + a2.
6. Если для начала одной из следующих работ необходимо выполнение не
всех входящих работ, а только некоторых, то следует ввести
дополнительное событие, дополнительную фиктивную работу, граф
перестроить в соответствии с рисунком:
Например: а подводка электричества, b подводка воды,
с подключение электроплиты, d подключение стиральной машины.
12
13.
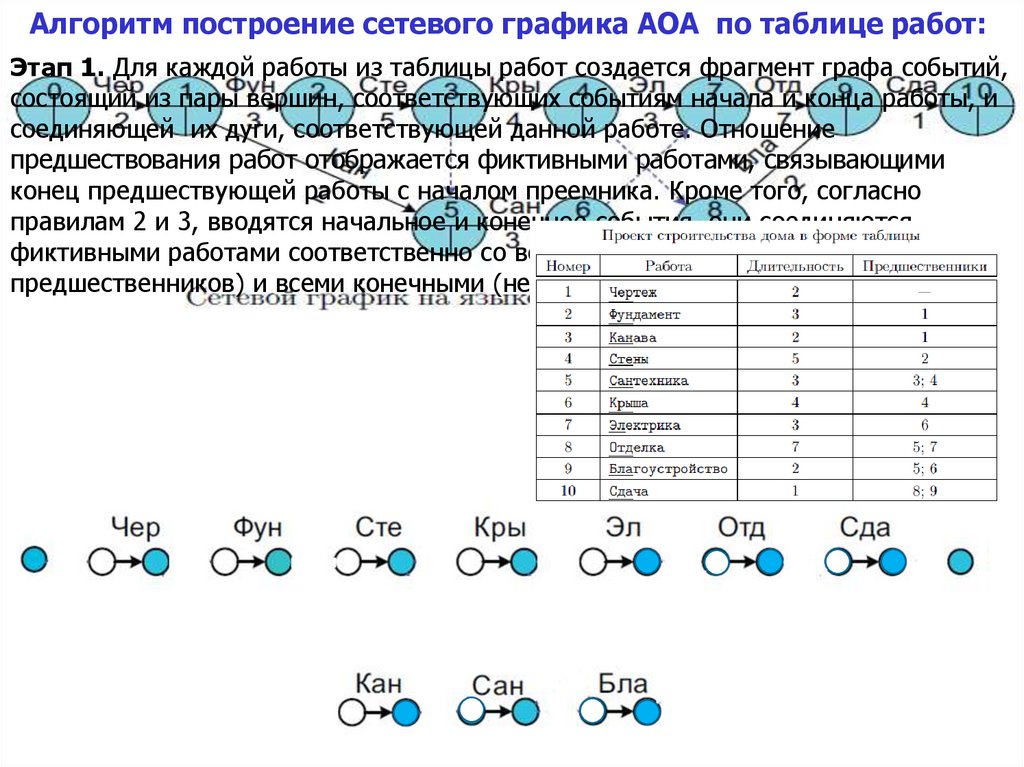
Алгоритм построение сетевого графика AOA по таблице работ:Этап 1. Для каждой работы из таблицы работ создается фрагмент графа событий,
состоящий из пары вершин, соответствующих событиям начала и конца работы, и
соединяющей их дуги, соответствующей данной работе. Отношение
предшествования работ отображается фиктивными работами, связывающими
конец предшествующей работы с началом преемника. Кроме того, согласно
правилам 2 и 3, вводятся начальное и конечное события, они соединяются
фиктивными работами соответственно со всеми начальными (не имеющими
предшественников) и всеми конечными (не имеющими преемников) работами.
13
14.
Этап 2. Удаление висячих вершин. Самый очевидный способ упрощенияграфа удаление «висячих» вершин, т.е. событий, у которых имеется одна
входящая и одна выходящая работа, причем обязательно одна из них
фиктивная. При этом необходимо следить за выполнением правила 4 и не
допускать образования параллельных ребер.
Возможные варианты расположения висячих вершин и соответствующие
способы преобразования графа приведены на рисунке:
Фиктивная работа при удалении висячей вершины объединяется с реальной
работой.
14
15.
Этап 3. Нумерация вершин ориентированного графа называется правильной,если все дуги направлены от вершин с меньшим номером к вершинам с большим
номером.
Правильная нумерация не единственна, приведенный ниже алгоритм, основанный на
разбиении вершин графа на ярусы (слои), производит одну из них. Этот же алгоритм
позволяет проверить граф на отсутствие орциклов.
Шаг 0. Назначаем номер яруса L = 0.
Шаг 1. Находятся все вершины, в которые не идет ни одна дуга. Если таких вершин
нет, переход на Шаг 4, иначе на Шаг 2.
Шаг 2. Если L = 0, то единственная вершина, отнесенная к ярусу 0, получает номер
0. Если L > 0, то вершины текущего яруса нумеруются в произвольном порядке,
продолжая нумерацию, выполненную на предыдущей итерации. Хотя здесь удобнее
придерживаться одного принципа – нумеровать сверху вниз или наоборот.
Шаг 3. Пронумерованные вершины мысленно отбрасываются вместе с
инцидентными (т.е. выходящими из них) дугами. Номер яруса увеличивается:
L = L+1. Возврат на Шаг 1.
Шаг 4. Если все вершины графа пронумерованы, то нормальное завершение
алгоритма. Если нет, то это означает, что в графе имеются орциклы и правильная
нумерация невозможна.
15
16.
После того как сетевая модель проекта построена, начинается этап его анализа.Анализ проекта может осуществляться, как минимум, с трех точек зрения:
с точки зрения времени выполнения (временной анализ), материальные и
стоимостные ресурсы при этом полагаются как бы неограниченными;
с точки зрения оптимального распределения ограниченных материальных
ресурсов (ресурсный анализ);
с точки зрения стоимости выполнение проекта — специфического и
важнейшего вида ресурса (стоимостной анализ).
Для таких видов анализа пригодна преимущественно сетевая модель АОА.
При этом временой анализ могут реализовывать алгоритмы как метода CPM, так и
метода PERT.
Эти же алгоритмы находят применение в наиболее распространенных
программных продуктах для управления проектами EPM (Enterprise Project
Managment), ERP (Enterprise Resource Planning):
• MS Project,
• Oracle Primavera
• и др.
16
17.
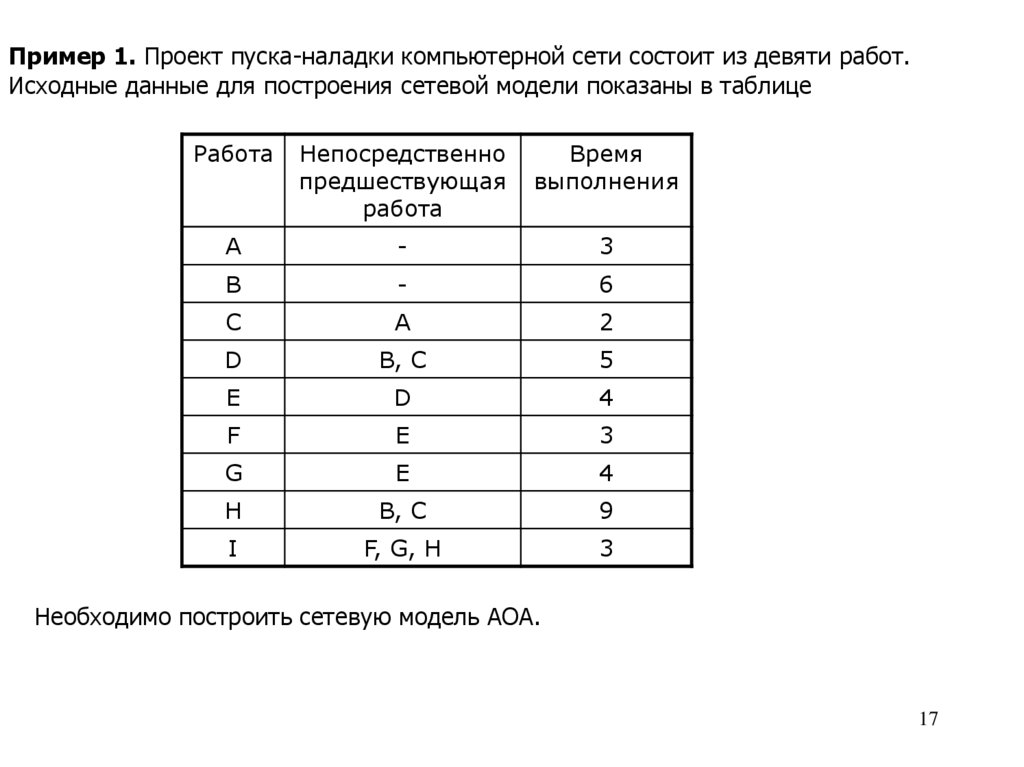
Пример 1. Проект пуска-наладки компьютерной сети состоит из девяти работ.Исходные данные для построения сетевой модели показаны в таблице
Работа
Непосредственно
предшествующая
работа
Время
выполнения
A
-
3
B
-
6
C
A
2
D
B, C
5
E
D
4
F
E
3
G
E
4
H
B, C
9
I
F, G, H
3
Необходимо построить сетевую модель АОА.
17
18.
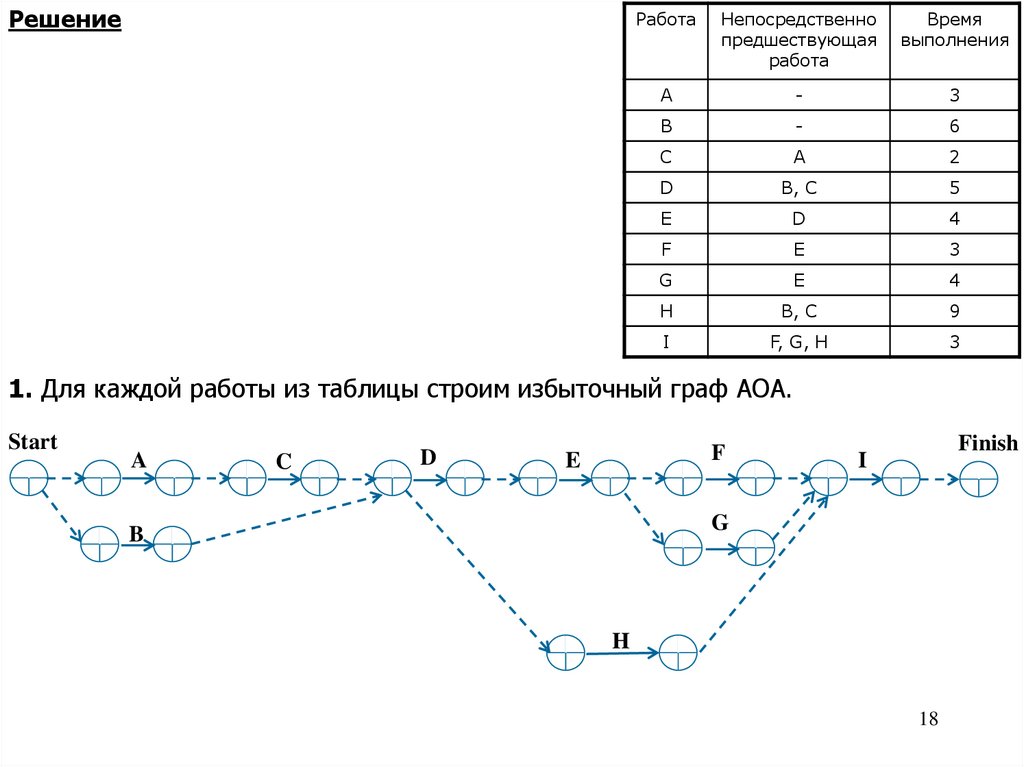
РешениеРабота
Непосредственно
предшествующая
работа
Время
выполнения
A
-
3
B
-
6
C
A
2
D
B, C
5
E
D
4
F
E
3
G
E
4
H
B, C
9
I
F, G, H
3
1. Для каждой работы из таблицы строим избыточный граф AOA.
Start
A
C
D
F
E
Finish
I
G
B
H
18
19.
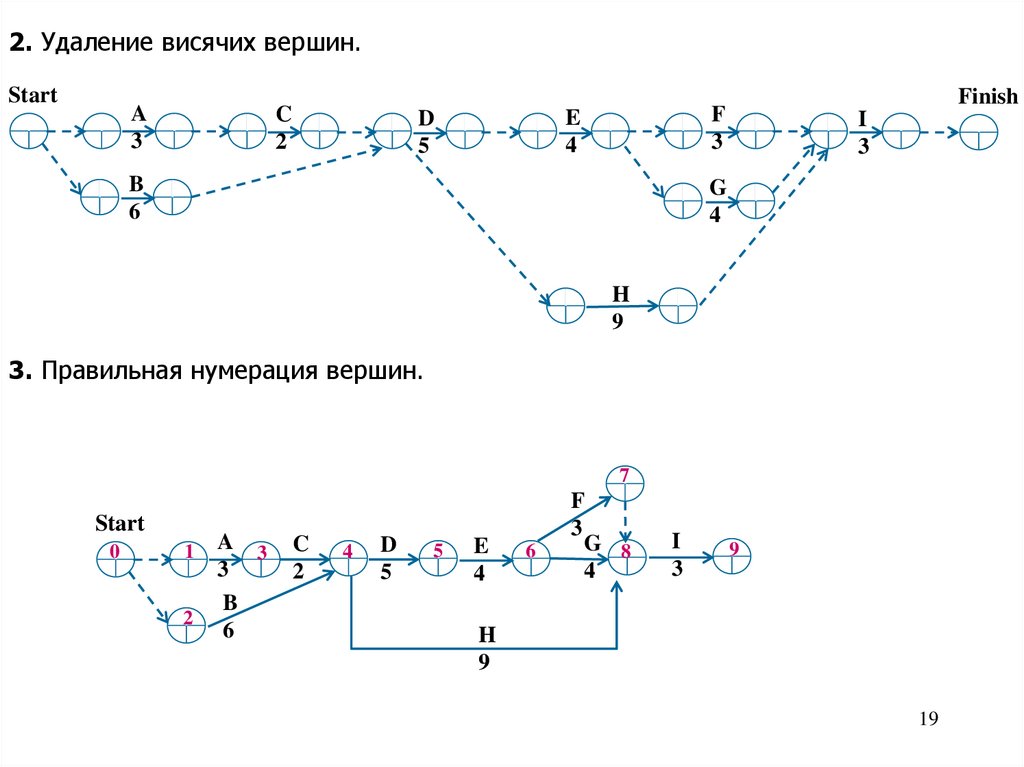
2. Удаление висячих вершин.Start
A
3
C
2
E
4
D
5
Finish
F
3
B
6
I
3
G
4
H
9
3. Правильная нумерация вершин.
7
Start
0
1
2
A 3
3
B
6
C
2
4
D
5
5
E
4
6
F
3
G 8
4
I
3
9
H
9
19
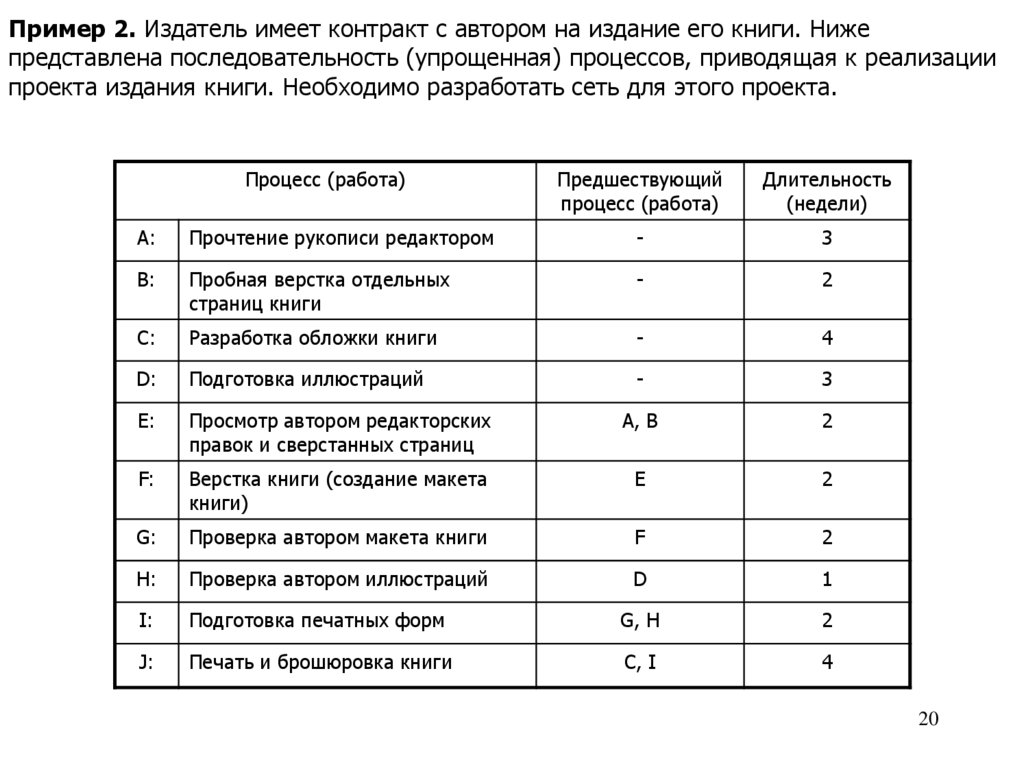
20.
Пример 2. Издатель имеет контракт с автором на издание его книги. Нижепредставлена последовательность (упрощенная) процессов, приводящая к реализации
проекта издания книги. Необходимо разработать сеть для этого проекта.
Процесс (работа)
Предшествующий
процесс (работа)
Длительность
(недели)
A:
Прочтение рукописи редактором
-
3
B:
Пробная верстка отдельных
страниц книги
-
2
C:
Разработка обложки книги
-
4
D:
Подготовка иллюстраций
-
3
E:
Просмотр автором редакторских
правок и сверстанных страниц
A, B
2
F:
Верстка книги (создание макета
книги)
E
2
G:
Проверка автором макета книги
F
2
H:
Проверка автором иллюстраций
D
1
I:
Подготовка печатных форм
G, H
2
J:
Печать и брошюровка книги
C, I
4
20
21.
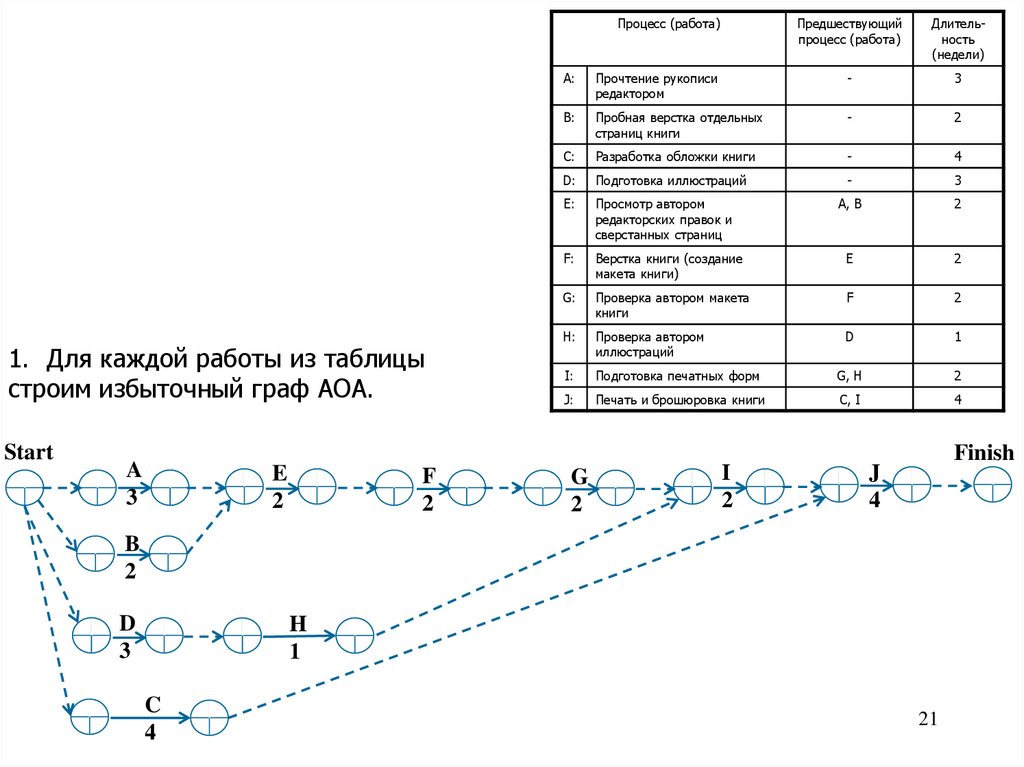
Процесс (работа)1. Для каждой работы из таблицы
строим избыточный граф AOA.
Start
A
3
E
2
F
2
Предшествующий
процесс (работа)
Длительность
(недели)
A:
Прочтение рукописи
редактором
-
3
B:
Пробная верстка отдельных
страниц книги
-
2
C:
Разработка обложки книги
-
4
D:
Подготовка иллюстраций
-
3
E:
Просмотр автором
редакторских правок и
сверстанных страниц
A, B
2
F:
Верстка книги (создание
макета книги)
E
2
G:
Проверка автором макета
книги
F
2
H:
Проверка автором
иллюстраций
D
1
I:
Подготовка печатных форм
G, H
2
J:
Печать и брошюровка книги
C, I
4
G
2
I
2
Finish
J
4
B
2
D
3
H
1
C
4
21
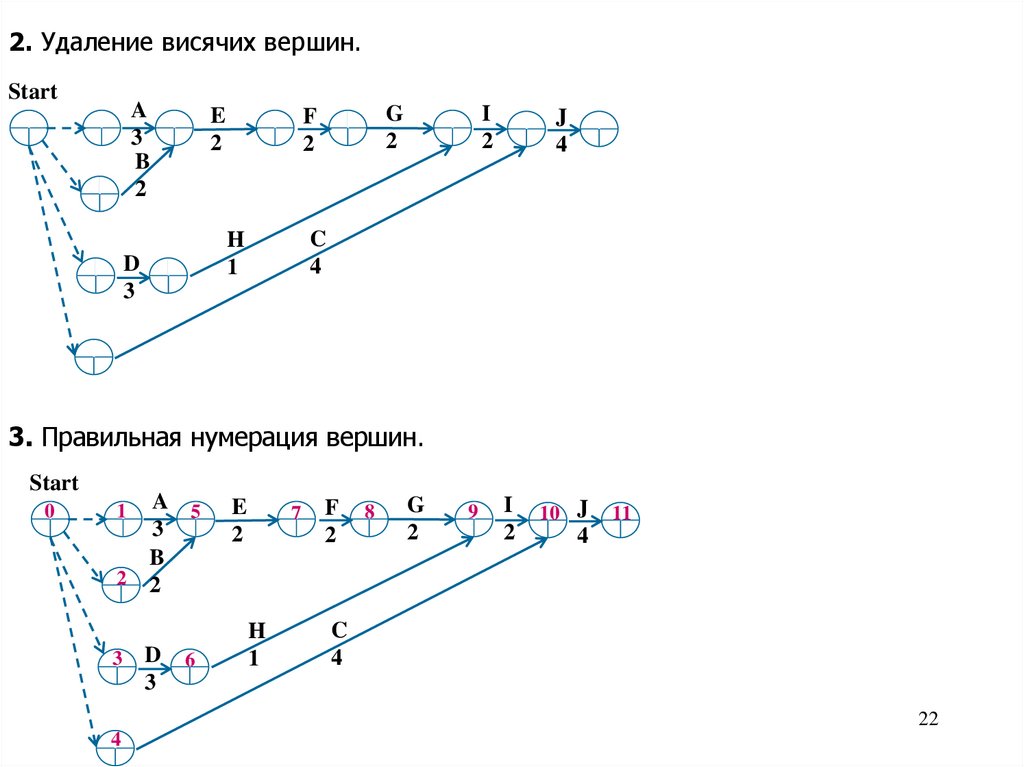
22.
2. Удаление висячих вершин.Start
A
3
B
2
E
2
J
4
C
4
H
1
D
3
I
2
G
2
F
2
3. Правильная нумерация вершин.
Start
0
1
2
3
A 5
3
B
2
D
3
6
E
2
7
H
1
F
2
8
G
2
9
I
2
10 J
11
4
C
4
22
4
23.
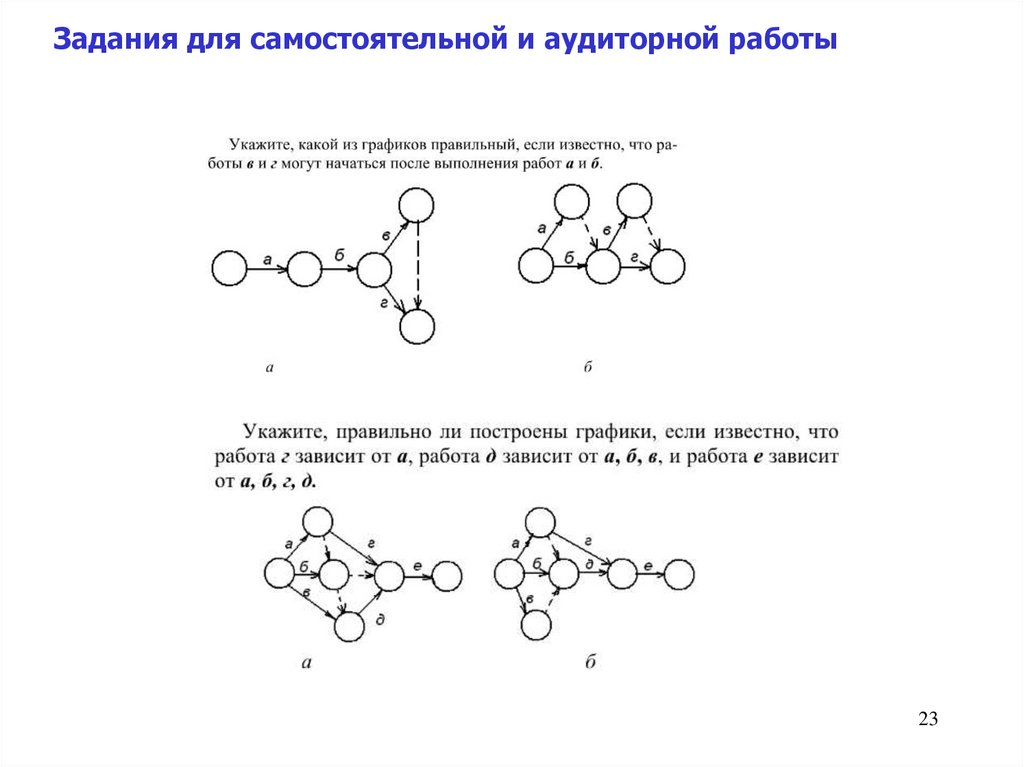
Задания для самостоятельной и аудиторной работы23
24.
Задания для самостоятельной и аудиторной работы1)
2)
3)
4)
5)
6)
24
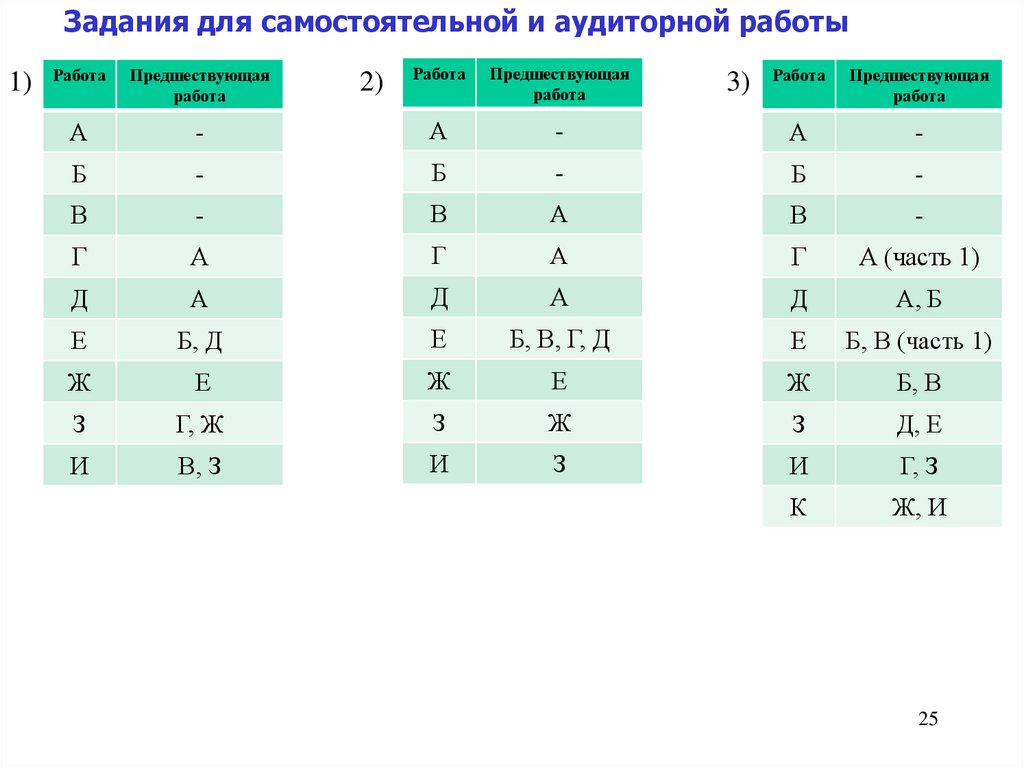
25.
Задания для самостоятельной и аудиторной работы1)
Работа
Предшествующая
работа
-
А
Б
-
В
Работа
Предшествующая
работа
Работа
Предшествующая
работа
А
-
А
-
Б
-
Б
-
-
В
А
В
-
Г
А
Г
А
Г
А (часть 1)
Д
А
Д
А
Д
А, Б
Е
Б, Д
Е
Б, В, Г, Д
Е
Б, В (часть 1)
Ж
Е
Ж
Е
Ж
Б, В
З
Г, Ж
З
Ж
З
Д, Е
И
В, З
И
З
И
Г, З
К
Ж, И
2)
3)
25
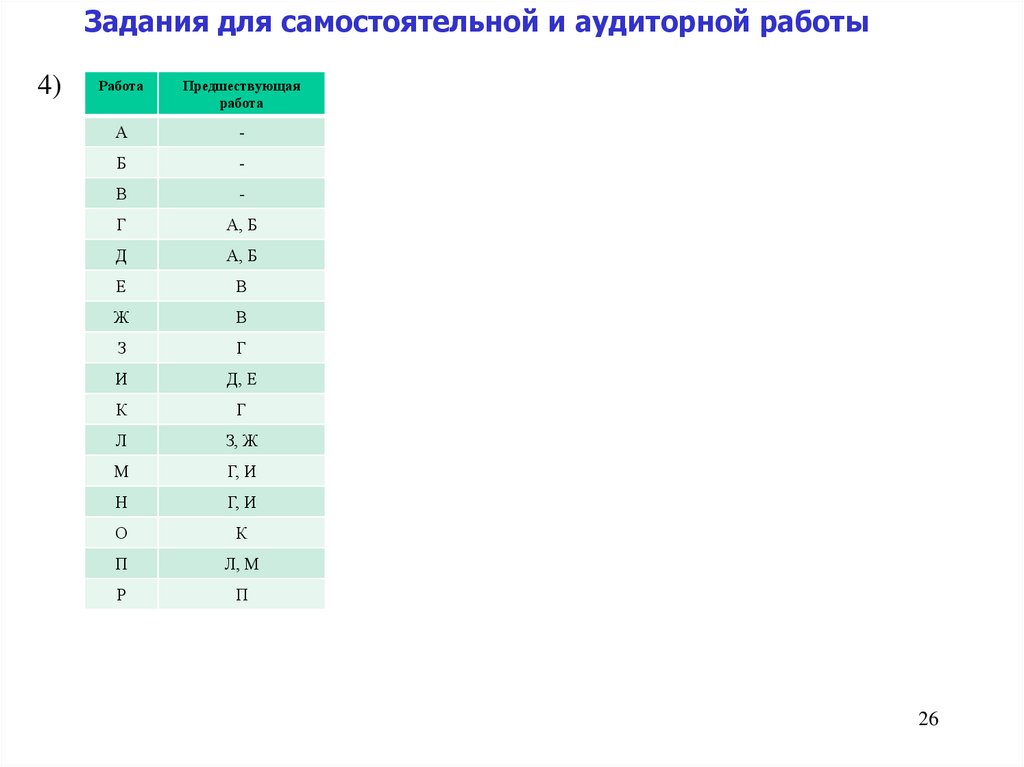
26.
Задания для самостоятельной и аудиторной работы4)
Работа
Предшествующая
работа
А
-
Б
-
В
-
Г
А, Б
Д
А, Б
Е
В
Ж
В
З
Г
И
Д, Е
К
Г
Л
З, Ж
М
Г, И
Н
Г, И
О
К
П
Л, М
Р
П
26
27.
1.2. Временной анализ проектаЦель временного анализа рассчитать ранние и поздние сроки наступления всех
событий, срок выполнения проекта в целом, с учетом возможного распараллеливания
работ, а также определить резервы времени для некритичных работ.
Принято считать, что отсчет времени начинается с начала проекта.
Ранним сроком (Early, earliest time) наступления некоторого события называется
наиболее раннее время, необходимое для выполнения в с е х работ,
предшествующих данному событию. Ранний срок любого события будет равен длине
длиннейшего (по времени) из путей, ведущих из начальной вершины в данное
событие. Ранний срок i-го события обозначается Ei.
Самый длинный из путей, ведущих из начальной вершины графа в конечную,
называется критическим путем (critical path).
Ранний срок конечного события проекта равен длине критического пути в сетевой
модели проекта и это время называется критическим временем проекта T.
Поздним сроком наступления события (Late, latest time) называется максимально
возможный момент наступления данного события при условии, что критическое время
проекта остается неизменным. Поздний срок i-го события обозначается Li.
Для любого i-го события всегда выполняется соотношение Ei ≤ Li.
27
28.
1.2.1. Метод критического пути (СРМ)В результате применения метода СРМ получаем следующую информацию:
1. Раннее Ei и позднее Li время наступления всех событий, общую длительность
выполнения проекта Т.
2. Разделение множества работ (процессов), составляющих проект, на критические и
некритические работы.
3. Резервы времени у некритических работ.
Работа является критической, если она не имеет резерва для времени своего
начала и завершения, в ином случае работа является некритической.
Таким образом, чтобы весь проект завершился без задержек, необходимо, чтобы все
критические работы начинались и заканчивались в строго определенное время. Любая
задержка критической работы приводит к задержке всего проекта, однако их доля в
крупном проекте может быть невелика. Поэтому внимание ЛПР не рассеивается на
множестве всех работ, а концентрируется на небольшом их числе.
Для некритической работы возможен некоторый «дрейф/сдвиг» (резерв) времени ее
начала, но в определенных границах, когда время ее начала не влияет на длительность
выполнения всего проекта.
Для проведения необходимых вычислений введем обозначения:
Ei ранний срок наступления i-го события, Li поздний срок наступления,
tij длительность работы / процесса (i, j).
28
29.
Вычисление критического пути включает два этапа (прохода): при проходе впередвычисляются ранние сроки наступления всех событий, а при проходе назад поздние
сроки наступления всех событий. При этом сетевая модель АОА должна обязательно
удовлетворять перечисленным выше 6 правилам построения, в т.ч. обязательно
должна быть выполнена правильная нумерация его вершин.
Проход вперед. Вычисления начинаются в узле 0 и заканчиваются в последнем
узле n. Движение осуществляем в порядке увеличения номеров вершин.
Начальный шаг. Полагаем E0 = 0; это указывает на то, что проект начинается в
нулевой момент времени.
Основной шаг j. Для узла j>0 определяем предшествующие узлы р, q, …, v
непосредственно связанные с узлом j работами (р, j), (q, j), …, (v, j), для которых уже
вычислены ВСЕ ранние сроки наступления соответствующих событий. Ранний срок
наступления события j вычисляется по формуле:
Ej = max{ Ep + tpj, Eq + tqj, ..., Ev + tvj }.
Проход вперед завершается, когда будет вычислена величина En для финишного
узла n. По определению величина Ej равна самому длинному пути (длительности)
от начала проекта до узла (события) j.
Ep p
Eq
Ev
tqj
q .
.
v .
tpj
j Ej
tvj
29
30.
Проход назад. В этом проходе вычисления начинаются в последнем узле n изаканчиваются в узле 0. Движение осуществляем в порядке уменьшения номеров
вершин.
Начальный шаг. Полагаем Ln = En ; это указывает, что ранний и поздний срок
для завершения проекта совпадают.
Основной шаг j. Для узла j определяем последующие узлы р, q, …, v
непосредственно связанные с узлом j процессами (j, p), (j, q), …, (j, v), для которых
уже вычислены ВСЕ поздние сроки наступления соответствующих событий.
Поздний срок наступления события j вычисляется по формуле
Lj = min {Lp - tjp, Lq - tjq, …, Lv - tjv }.
Проход назад завершается при вычислении величины L0 для узла 0.
i
Ei Li
tij
j
Ej Lj
Lj
Работа (i, j) будет критической, если одновременно
выполняются все три условия:
1. Ei = Li ,
2. Ej = Lj ,
3. Lj - Li = Ej - Ei = tij
tjp
j
tjq
tjv
p
Lp
Lq
q
.
.
.
v Lv
Если хотя бы одно из этих условий не выполняется, то работа будет некритической.
Критические работы должны образовывать непрерывный (возможно через
30
фиктивные работы) путь через всю сеть от начального события до конечного.
31.
Пример 3. Найти критический путь для сети проекта, показанной на рисунке.Длительность всех процессов дана в днях.
Проход вперед:
Узел 0. E0 = 0.
Узел 1. E1 = E0 + t01 = 0 + 2 = 2.
Узел 2. E2 = E1 + t12 = 2 + 3 = 5.
Узел 3. E3 = E2 + t23 = 5 + 5 = 10.
Узел 4. E4 = E3 + t34 = 10 + 4 = 14.
Узел 5. E5 = max{E1 + t15 , E3 + t35} = max{2 + 2, 10 + 0} = 10.
Узел 6. E6 = E5 + t56 = 10 + 3 = 13.
Узел 7. E7 = max{E4 + t47 , E6 + t67} = max{14 + 3, 13 + 0} = 17.
Узел 8. E8 = max{E4 + t48 , E6 + t68} = max{14 + 0, 13 + 0} = 14.
Узел 9. E9 = max{E7 + t79 , E8 + t89} = max{17 + 7, 14 + 2} = 24.
Узел 10. E10 = E9 + t9,10 = 24 + 1 = 25.
T= E10 = 25 дней – время выполнения проекта (критическое время проекта).
31
32.
0 02 2
5 5
10 10
14 14
17 17
10 14
13 17
14 22
24 24
25 25
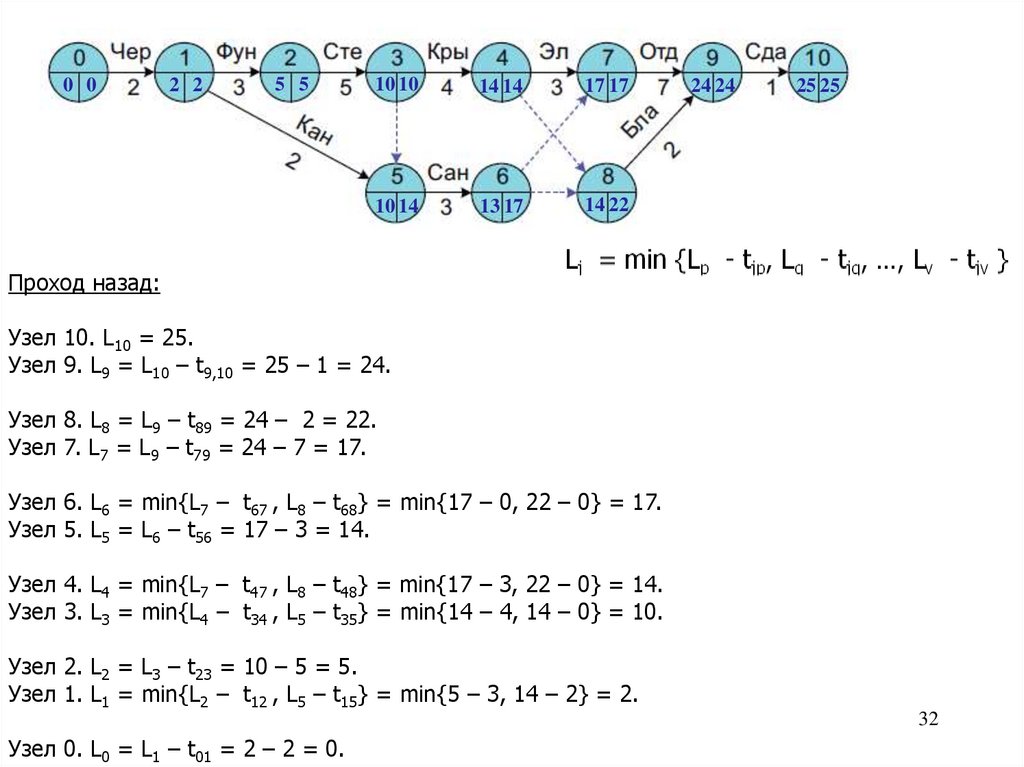
Проход назад:
Узел 10. L10 = 25.
Узел 9. L9 = L10 – t9,10 = 25 – 1 = 24.
Узел 8. L8 = L9 – t89 = 24 – 2 = 22.
Узел 7. L7 = L9 – t79 = 24 – 7 = 17.
Узел 6. L6 = min{L7 – t67 , L8 – t68} = min{17 – 0, 22 – 0} = 17.
Узел 5. L5 = L6 – t56 = 17 – 3 = 14.
Узел 4. L4 = min{L7 – t47 , L8 – t48} = min{17 – 3, 22 – 0} = 14.
Узел 3. L3 = min{L4 – t34 , L5 – t35} = min{14 – 4, 14 – 0} = 10.
Узел 2. L2 = L3 – t23 = 10 – 5 = 5.
Узел 1. L1 = min{L2 – t12 , L5 – t15} = min{5 – 3, 14 – 2} = 2.
32
Узел 0. L0 = L1 – t01 = 2 – 2 = 0.
33.
0 02 2
5 5
10 10
14 14
17 17
10 14
13 17
14 22
24 24
25 25
Работа (i, j) будет критической, если одновременно выполняются три условия:
1. Ei = Li ,
2. Ej = Lj ,
3. Lj - Li = Ej - Ei = tij
Таким образом критическими работами будут работы, обозначенные красной
стрелкой.
Отметим, что в литературе по сетевому планированию и управлению, и в
прикладных программах, встречаются также следующие обозначения:
ESij = Ei — раннее начало (early start);
EFij = Ei + tij — раннее окончание (early finish);
LSij = Lj − tij — позднее начало (late start);
LFij = Lj — позднее окончание (late finish).
33
34.
Задания для самостоятельной и аудиторной работыВыполнить расчет методом СРМ.
6
1)
2)
3)
1
34
35.
1.2.2. Построение временного графикаВременной график (диаграмма Ганта) строится после вычисления раннего и
позднего срока наступления всех событий сети и включает в себя два этапа:
1) построение предварительного графика по выбранной стратегии (ALAP / ASAP,
комбинированная);
2) построение окончательного графика с учетом правила «красного флажка».
i
Ei Li
tij
j
Ej Lj
Пара величин (Ei , Lj ) ограничивает максимальный интервал времени, в
течение которого может выполняться процесс (i, j).
Предварительный временной график проекта можно начертить, используя
максимальные интервалы выполнения каждого процесса (процессы располагаются
последовательно друг за другом согласно логике предшествования):
1. Критические процессы (показывают на графике красными сплошными
линиями/барами). Их суммарная длительность равна длительности выполнения
всего проекта.
2. Некритические процессы (показываются на графике пунктирными линиями /
барами иного цвета) представлены максимальными интервалами выполнения,
которые могут превышать реальную длительность выполнения этих процессов.
35
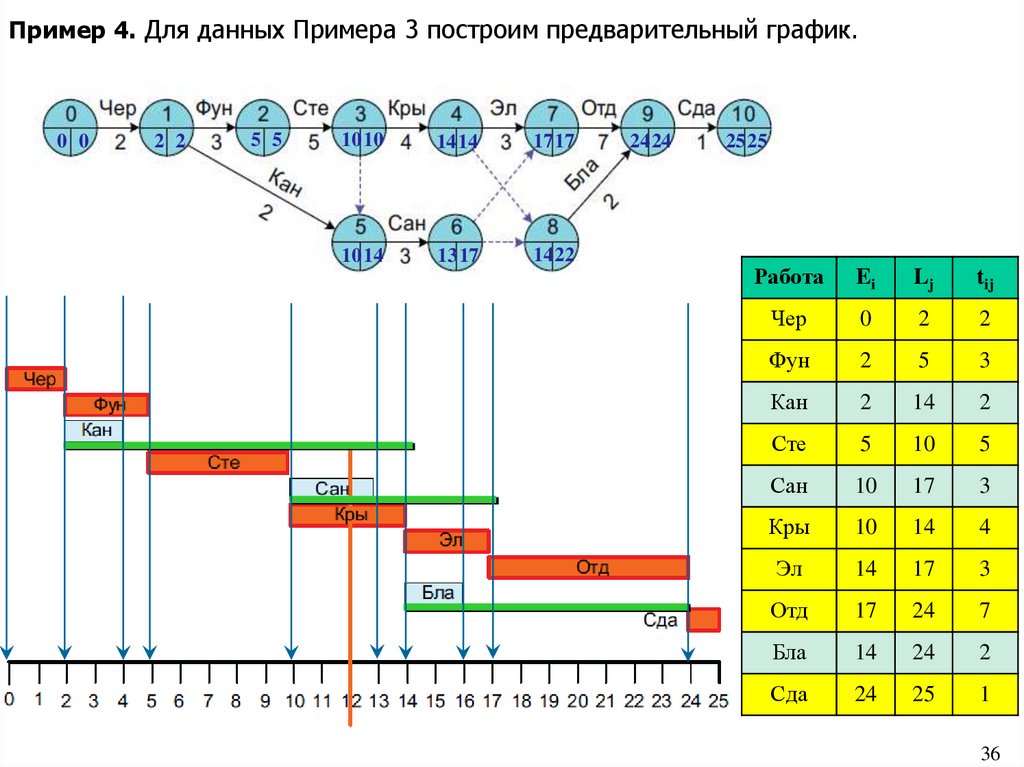
36.
Пример 4. Для данных Примера 3 построим предварительный график.0 0
2 2
5 5
10 10
14 14
17 17
10 14
13 17
14 22
24 24
25 25
Работа
Ei
Lj
tij
Чер
0
2
2
Фун
2
5
3
Кан
2
14
2
Сте
5
10
5
Сан
10
17
3
Кры
10
14
4
Эл
14
17
3
Отд
17
24
7
Бла
14
24
2
Сда
24
25
1
36
37.
Для построение окончательного графика необходимо определить запасы времени. Запасвремени некритического процесса это часть максимального интервала времени выполнения
этого процесса. Различают полный (общий) и свободный запас (резерв) времени
процесса/работы.
Полный запас времени работы i, j (Total Float) TFij – это время, на которое в общем случае
можно задержать ее выполнение при условии, что критическое время останется неизменным:
TFij = Lj - Ei - tij .
Свободный запас времени
работы i, j (Free Float) FFij – это время, на
которое можно задержать ее выполнение при
условии, что ранний срок события,
соответствующего моменту окончания данной
работы, останется неизменным :
По определению FFij ≤ TFij .
i
Ei Li
tij
j
Ej Lj
FFij = Ej - Ei - tij .
Принципиальное отличие свободного резерва от полного состоит в том, что свободный
резерв каждая работа может использовать по своему усмотрению, все равно он пропадает
зря, потому что ранний срок наступления последующего события не может быть меньше изза других работ. Полный же резерв нужно использовать с осторожностью: если одна работа
выбрала весь полный резерв времени и тем самым оказалась на критическом пути, то другие
работы, попавшие на тот же критический путь, удлинять невозможно, иначе сорвется срок
всего проекта. Использование сдвигов некритических работ зачастую позволяет согласовать
(удовлетворить) ограничениям на трудовые ресурсы, задействованные на соответствующих
37
работах. Если такие ограничения имеют место.
38.
Если процесс/работа имеет свободный резерв, то ее можно по-разномурасположить на отрезке времени, отведенном на ее выполнение:
1) работу можно начать скоро как только возможно (стратегия As Soon As
Possible – ASAP), т. е. как только будут завершены все предшествующие по
технологии работы. Такая стратегия описывается народной мудростью
«Никогда не откладывай на завтра то, что можно сделать сегодня»;
2) работу можно начать позднее как только возможно (стратегия As Late As
Possible – ALAP), т.е. тянуть с началом работы до последнего мгновения,
растрачивая на ожидание работы весь свободный резерв времени;
3) комбинированная стратегия – исходя из тех или иных соображений,
tij сместить
i
j
работу на некоторую величину, не превышающую величину
свободного
Ei Li
Ej Lj
резерва.
Правило «красного флажка». Для некритического процесса (i, j)
а) если FFij = TFij , то данный процесс может выполняться в любое время внутри
максимального интервала (Ei , Lj) без нарушения отношений следования;
б) если FFij < TFij , то без нарушения отношений следования данный процесс может
начаться со сдвигом, не превышающим FFij, относительно раннего срока начала
события Ei. Сдвиг начала процесса на величину времени d+ FFij, превышающую
FFij (но не более TFij ), должен сопровождаться равным сдвигом относительно Ej
всех процессов, начинающихся с события j на величину d. При этом начало
процесса (i,j) сдвигается на величину FFij + d.
38
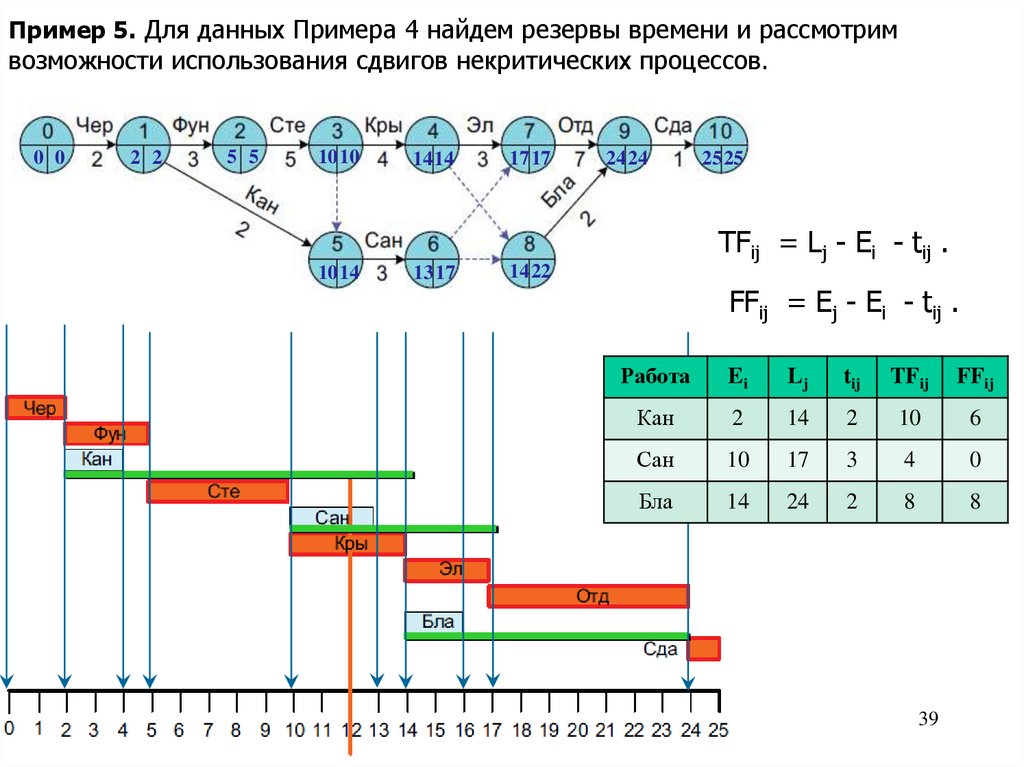
39.
Пример 5. Для данных Примера 4 найдем резервы времени и рассмотримвозможности использования сдвигов некритических процессов.
0 0
2 2
5 5
10 10
14 14
17 17
24 24
25 25
TFij = Lj - Ei - tij .
10 14
13 17
14 22
FFij = Ej - Ei - tij .
Работа
Ei
Lj
tij
TFij
FFij
Кан
2
14
2
10
6
Сан
10
17
3
4
0
Бла
14
24
2
8
8
39
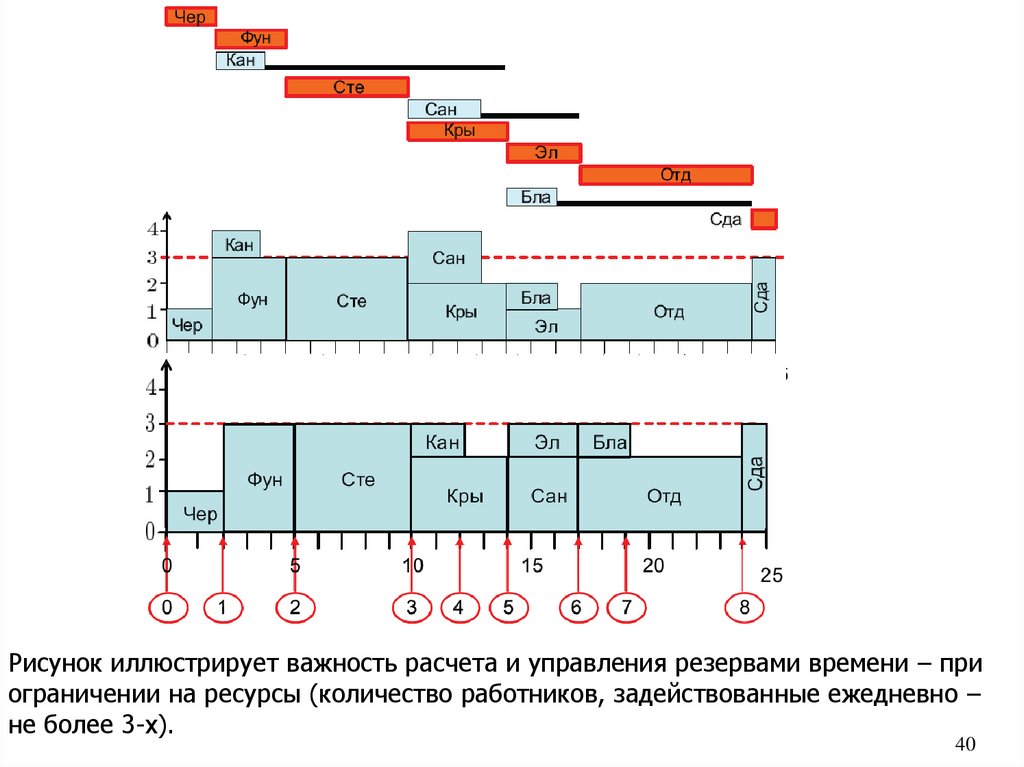
40.
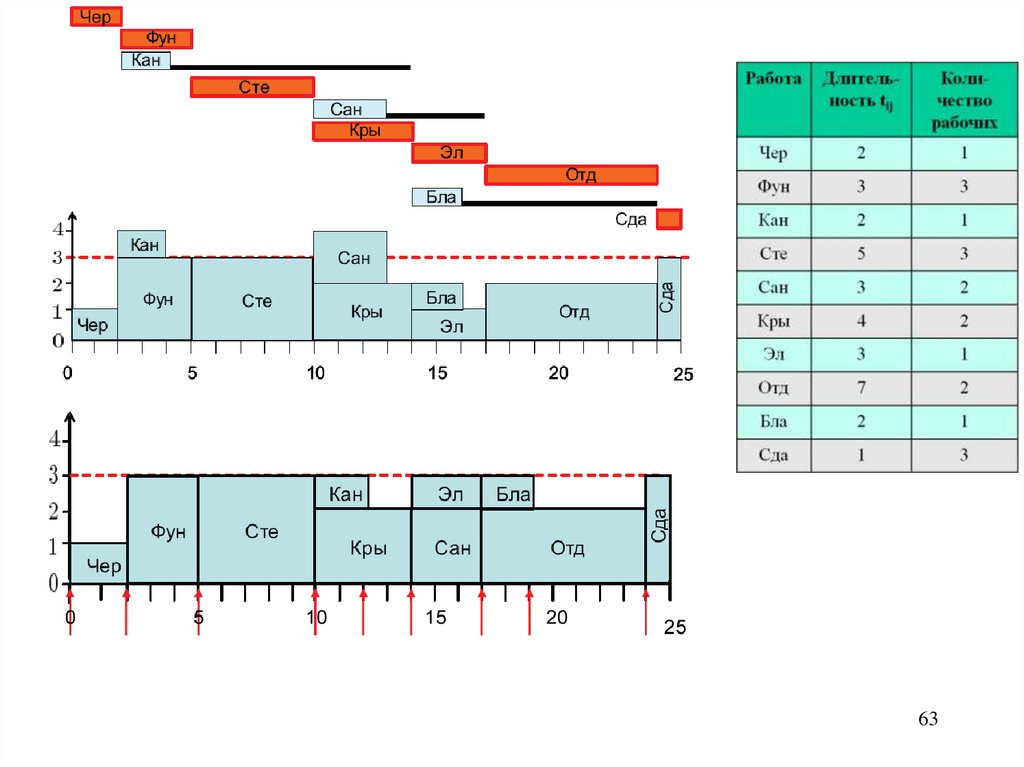
Рисунок иллюстрирует важность расчета и управления резервами времени – приограничении на ресурсы (количество работников, задействованные ежедневно –
не более 3-х).
40
41.
Задание для самостоятельной работы1. Выполнить расчет резервов времени и построить временной график для
исходных данных Примера 2.
2. Выполнить расчет резервов времени и построить временной график для
исходных данных Примера 1.
41
42.
Модель Примера 2.Start
0
1
2
3
A 5
3
B
2
D
3
6
E
2
7
H
1
F
2
8
G
2
9
I
2
10 J
11
4
C
4
4
42
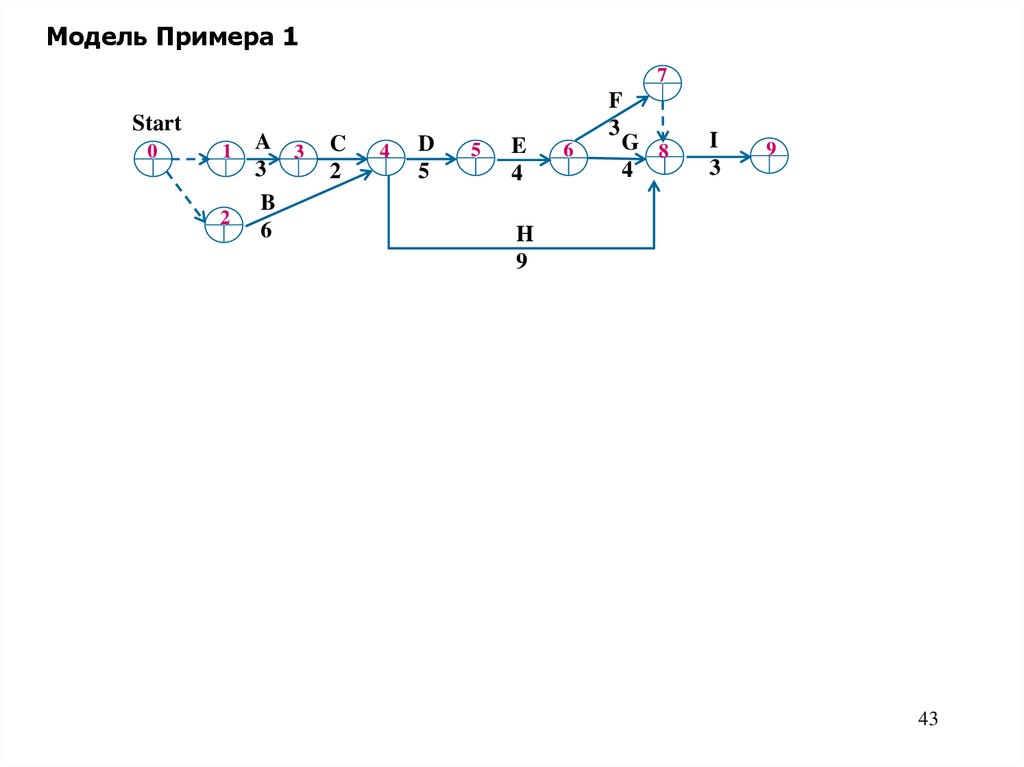
43.
Модель Примера 17
Start
0
1
2
A 3
3
B
6
C
2
4
D
5
5
E
4
6
F
3
G 8
4
I
3
9
H
9
43
44.
1.2.3. Метод PERTВ методе СРМ длительности работ являются известными величинами, которые могут
быть достаточно точно оценены тем или иным способом. Такая ситуация характерна
для рутинных проектов. Однако бывают случаи, когда это невозможно сделать, потому
что сам проект носит экспериментальный характер, а длительности работ могут
зависеть от многих непредсказуемых факторов и допускают весьма расплывчатые
оценки. В таких случаях их целесообразно рассматривать как случайные величины и
применять к анализу проектов вероятностный подход. Для такого анализа и разработан
метод PERT — Program Evaluation and Review Technique (техника оценки и обзора
программ).
Априори известно:
— во-первых, по своей физической сути длительность любой работы tij представляет
собой положительную непрерывную случайную величину, распределенную в
ограниченном промежутке tijmin , tijmax ;
— во-вторых, модельная плотность распределения pij(t) должна быть непрерывной
унимодальной функцией, имеющей максимум внутри диапазона tijmin , tijmax и равной нулю
вне его.
Авторы классического метода PERT, проанализировав обширный фактический материал
(хронометражи отдельных видов работ, нормативные данные и т. д.), выбрали в
качестве модельного распределения плотности распределения случайных величин
бета-распределение (В-распределение).
44
45.
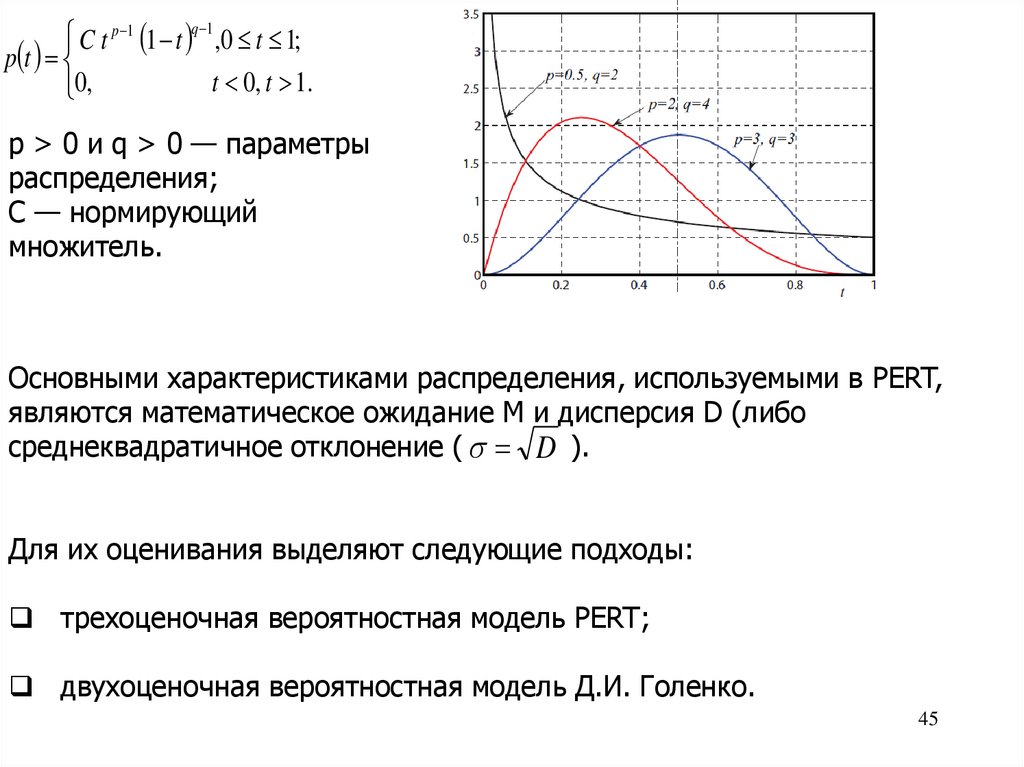
C t p 1 1 t q 1 ,0 t 1;p t
t 0, t 1.
0,
p > 0 и q > 0 — параметры
распределения;
C — нормирующий
множитель.
Основными характеристиками распределения, используемыми в PERT,
являются математическое ожидание M и дисперсия D (либо
среднеквадратичное отклонение ( D ).
Для их оценивания выделяют следующие подходы:
трехоценочная вероятностная модель PERT;
двухоценочная вероятностная модель Д.И. Голенко.
45
46.
Трехоценочная вероятностная модель PERT.Исторически первая, ставшая классической, вероятностная модель PERT
min
предлагает эксперту для каждой работы наряду с оптимистической a tij и
max
пессимистической b tij оценками длительности работы указать третью —
наиболее вероятную длительность работы (most likely performance time) m,
соответствующую моде бета-распределения (точке локального
максимума плотности распределения).
Авторы этой модели сделали допущение о том, что для всех работ
p + q ≈ 6. Тогда для каждой работы можем вычислить:
1) математическое ожидание
2) дисперсию
a b 4m
M
6
a b 4 m a b
2
D
28
63
2
2
Имеет место более простая формула для дисперсии:
2
b a
D
36
46
47.
Двухоценочная вероятностная модель Д.И. Голенко.Требование к исполнителям работ / экспертам задавать три временные оценки
является весьма жестким, причем особые трудности вызывает необходимость
задания моды распределения, которая зависит от параметров плотности
распределения. Особенно в случае работ, по которым не накоплена
достаточная статистика.
В связи с этим были разработаны многочисленные модификации
классической модели PERT. Одной из самых простых и удачных является модель
на основе двух оценок, предложенная в середине 1960-х гг. известным
советским математиком Д.И. Голенко.
Эта модель предполагает еще более сильное по сравнению с PERT допущение:
параметры p и q должны быть одинаковыми для всех работ
проекта. Проведенные автором многочисленные эмпирические исследования
показали, что величины p и q, усредненные по большому количеству сетевых
проектов, концентрируются около постоянных значений p ≈ 2, q ≈ 3.
Таким образом, задавая параметры a и b находим:
3a 2b
M
5
2
b a
D
25
2a b
m
3
47
48.
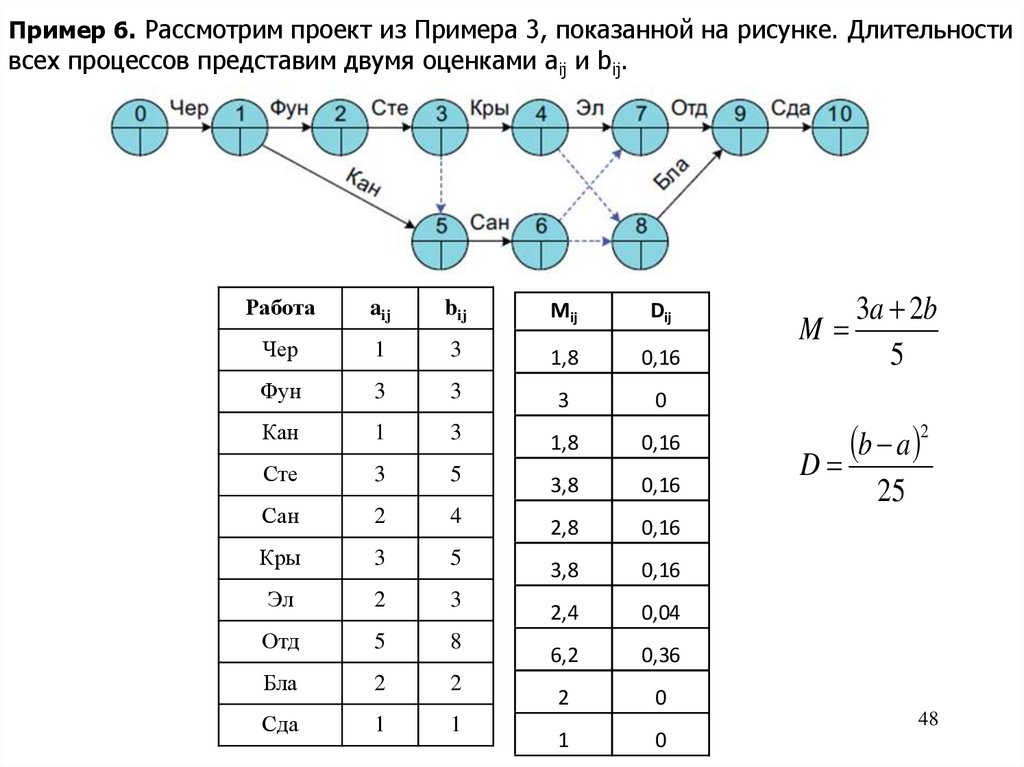
Пример 6. Рассмотрим проект из Примера 3, показанной на рисунке. Длительностивсех процессов представим двумя оценками aij и bij.
Работа
aij
bij
Mij
Dij
Чер
1
3
1,8
0,16
Фун
3
3
3
0
Кан
1
3
1,8
0,16
Сте
3
5
3,8
0,16
Сан
2
4
2,8
0,16
Кры
3
5
3,8
0,16
Эл
2
3
2,4
0,04
Отд
5
8
6,2
0,36
Бла
2
2
2
0
Сда
1
1
M
3a 2b
5
2
b a
D
25
48
1
0
49.
Оценка параметров проекта в целом. Методика PERT.После того как с помощью той или иной вероятностной модели оценены
математические ожидания Mij и дисперсии Dij длительностей всех работ, можно
провести расчет параметров проекта в целом. Поскольку все длительности
случайные, то раннее время Ek наступления любого k-го события, равное длине
длиннейшего пути из начальной вершины в k-ю, в том числе критическое время
всего проекта T = En , становятся случайными.
Основным допущением классической методики PERT является предположение о
том, что случайные вариации длительности работ вокруг средних значений не
меняют конфигурацию длиннейших путей, т. е. множество дуг сетевой модели
проекта, образующих длиннейший путь из начальной вершины в выбранную k-ю,
остается неизменным, случайной является только длина пути.
Алгоритм методики PERT.
Этап 1 (построение «усредненной» сетевой модели).
Строится обычная, детерминированная сетевая модель, в которой длительности
работ устанавливаются равными математическим ожиданиям Mij случайных
длительностей.
49
50.
Этап 2 (вычисление ранних сроков и отслеживание длиннейшего пути).Проходом вперед метода СРМ временного анализа вычисляются ранние сроки всех
событий Ek. Список дуг критического пути строится обратным ходом от выбранной
k-й вершины к началу сети (как правило, от конечной вершины сети).
После нахождения критического пути ЛПР может ставить вопросы о вычислении
основных параметров, имеющих отношение к k-му событию:
• среднее ожидаемое время наступления события M[Ek];
• дисперсия времени наступления события D[Ek];
• вероятность наступления события в установленные сроки.
Первые два параметра легко определить, используя свойства математического
ожидания и дисперсии суммы случайных величин:
M Ek M tij
( i , j ) Lk
D Ek D tij
( i , j ) Lk
Lk множество дуг сети, входящих в критический путь от начальной
до k-й вершины.
50
51.
Вероятность того, что время наступления k-го события Ek не превыситфиксированного заданного значения T0, равна
T M E
k
P Ek T0 0
D Ek
где Φ(x) — специальная, не выражающаяся через элементарные, функция
стандартного нормального распределения.
Иногда ставится обратная задача: определить срок Tk, в течение которого k-е
событие произойдет с гарантированной вероятностью P, достаточно близкой к 1,
например 0,9 или 0,95. В этом случае искомое значение рассчитывается по
формуле
Tk P M Ek P D Ek
здесь P — функция, обратная функции стандартного нормального
распределения. Вот ее несколько типичных значений: Ψ(0,9) = 1,28;
Ψ(0,95) = 1,64; Ψ(0,99) = 2,32.
Отметим, что значения функций x , P можно найти во многих книгах
по теории вероятностей и статистике.
В Matlab функция normcdf(x,0,1) вычисляет Φ(x), а norminv(р,0,1) Ψ(р).
В Excel : Φ(x) по НОРМСТРАСП(х), Ψ(р) по НОРМСТОБР(р).
51
52.
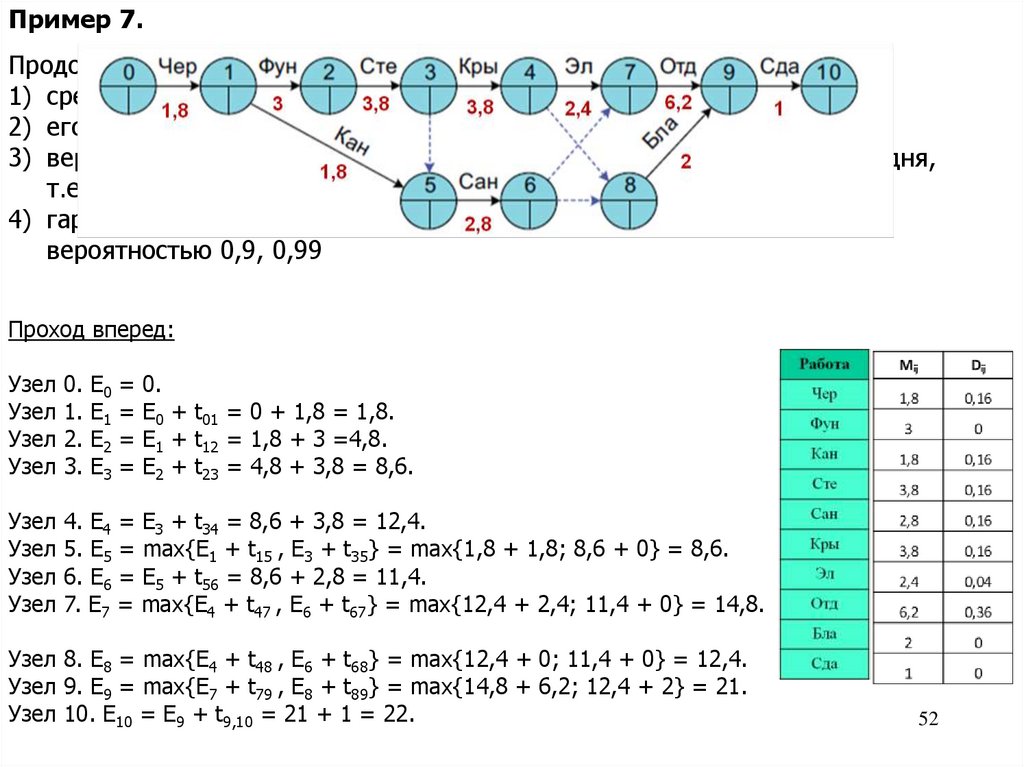
Пример 7.Продолжая Пример 6, найдем:
1) среднее ожидаемое время окончания проекта M[E10];
2) его стандартное отклонение σ[E10];
3) вероятность того, что строительство дома будет закончено за 20, 24 дня,
т.е. P(E10 < 20), P(E10 < 24);
4) гарантированный срок T0, в течение которого дом будет построен с
вероятностью 0,9, 0,99
Проход вперед:
Узел 0. E0 = 0.
Узел 1. E1 = E0 + t01 = 0 + 1,8 = 1,8.
Узел 2. E2 = E1 + t12 = 1,8 + 3 =4,8.
Узел 3. E3 = E2 + t23 = 4,8 + 3,8 = 8,6.
Узел 4. E4 = E3 + t34 = 8,6 + 3,8 = 12,4.
Узел 5. E5 = max{E1 + t15 , E3 + t35} = max{1,8 + 1,8; 8,6 + 0} = 8,6.
Узел 6. E6 = E5 + t56 = 8,6 + 2,8 = 11,4.
Узел 7. E7 = max{E4 + t47 , E6 + t67} = max{12,4 + 2,4; 11,4 + 0} = 14,8.
Узел 8. E8 = max{E4 + t48 , E6 + t68} = max{12,4 + 0; 11,4 + 0} = 12,4.
Узел 9. E9 = max{E7 + t79 , E8 + t89} = max{14,8 + 6,2; 12,4 + 2} = 21.
Узел 10. E10 = E9 + t9,10 = 21 + 1 = 22.
52
53.
0 01,8
1,8 1,8 3
4,8 4,8 3,8 8,6 8,6
14,8 14,86,2 21 21
3,812,4 12,42,4
1
22 22
2
1,8
8,6 12
2,8
11,4 14,8
12,4 19
Проход назад:
Узел 10. L10 = 22.
Узел 9. L9 = L10 – t9,10 = 22 – 1 = 21.
Узел 8. L8 = L9 – t89 = 21 – 2 = 19.
Узел 7. L7 = L9 – t79 = 21 – 6,2 = 14,8.
Узел 6. L6 = min{L7 – t67 , L8 – t68} = min{14,8 – 0, 19 – 0} = 14,8.
Узел 5. L5 = L6 – t56 = 14,8 – 2,8 = 12.
Узел 4. L4 = min{L7 – t47 , L8 – t48} = min{14,8 – 2,4; 19 – 0} = 12,4.
Узел 3. L3 = min{L4 – t34 , L5 – t35} = min{12,4 – 3,8; 12 – 0} = 8,6.
Узел 2. L2 = L3 – t23 = 8,6 – 3,8 = 4,8.
Узел 1. L1 = min{L2 – t12 , L5 – t15} = min{4,8 – 3; 12 – 1,8} = 1,8.
53
Узел 0. L0 = L1 – t01 = 1,8 – 1,8 = 0.
54.
0 01,8 1,8 3
1,8
4,8 4,8 3,8 8,6 8,6
14,8 14,86,2 21 21
3,812,4 12,42,4
1
22 22
2
1,8
8,6 12
2,8
11,4 14,8
12,4 19
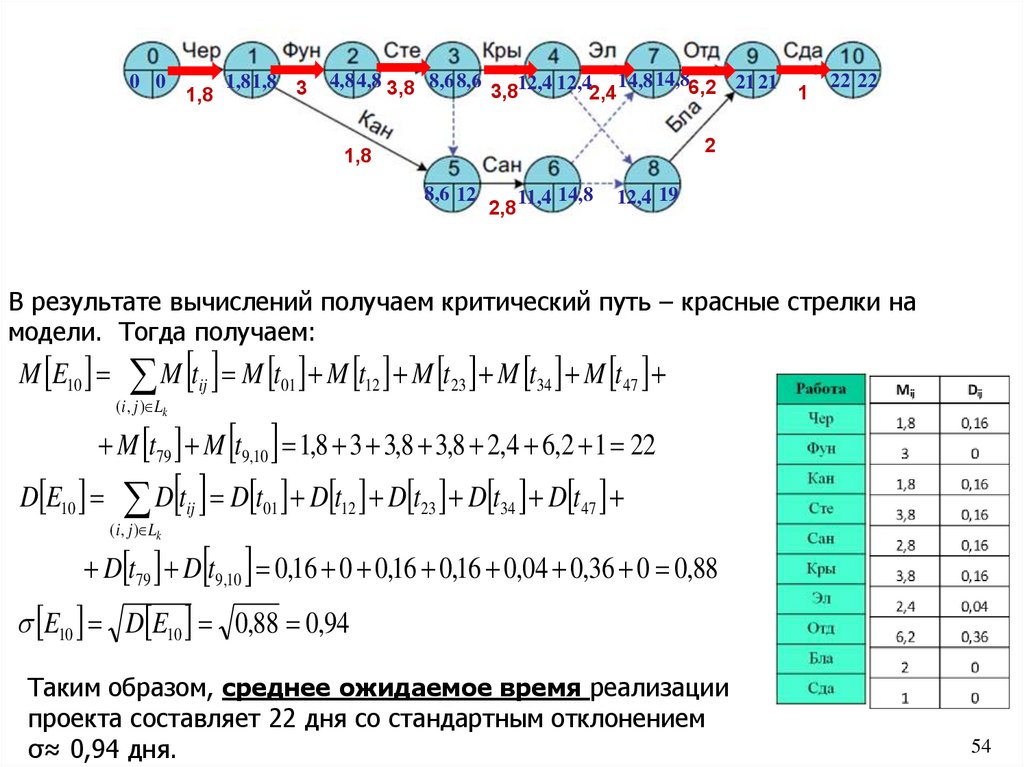
В результате вычислений получаем критический путь – красные стрелки на
модели. Тогда получаем:
M E10 M tij M t01 M t12 M t23 M t34 M t47
( i , j ) Lk
M t79 M t9,10 1,8 3 3,8 3,8 2,4 6,2 1 22
D t D t 0,16 0 0,16 0,16 0,04 0,36 0 0,88
D E10 D tij D t01 D t12 D t23 D t34 D t47
( i , j ) Lk
79
9 ,10
E10 D E10 0,88 0,94
Таким образом, среднее ожидаемое время реализации
проекта составляет 22 дня со стандартным отклонением
σ≈ 0,94 дня.
54
55.
При этом вероятность завершить проект за 20 дней равна:T0 M E10
20 22
P E10 20
2,13 1 2,13 0,0165
0,94
E10
При этом вероятность завершить проект за 24 дня равна:
T0 M E10
24 22
P E10 24
2,132 0,983
0,94
E10
Гарантированное с вероятностью 0,9 и 0,99 время завершения проекта:
Tk P M Ek P Ek
Tk 0,9 M E10 0,9 E10 22 1,2816 0,94 23,2
Tk 0,99 M E10 0,99 E10 22 2,3263 0,94 24,19
55
56.
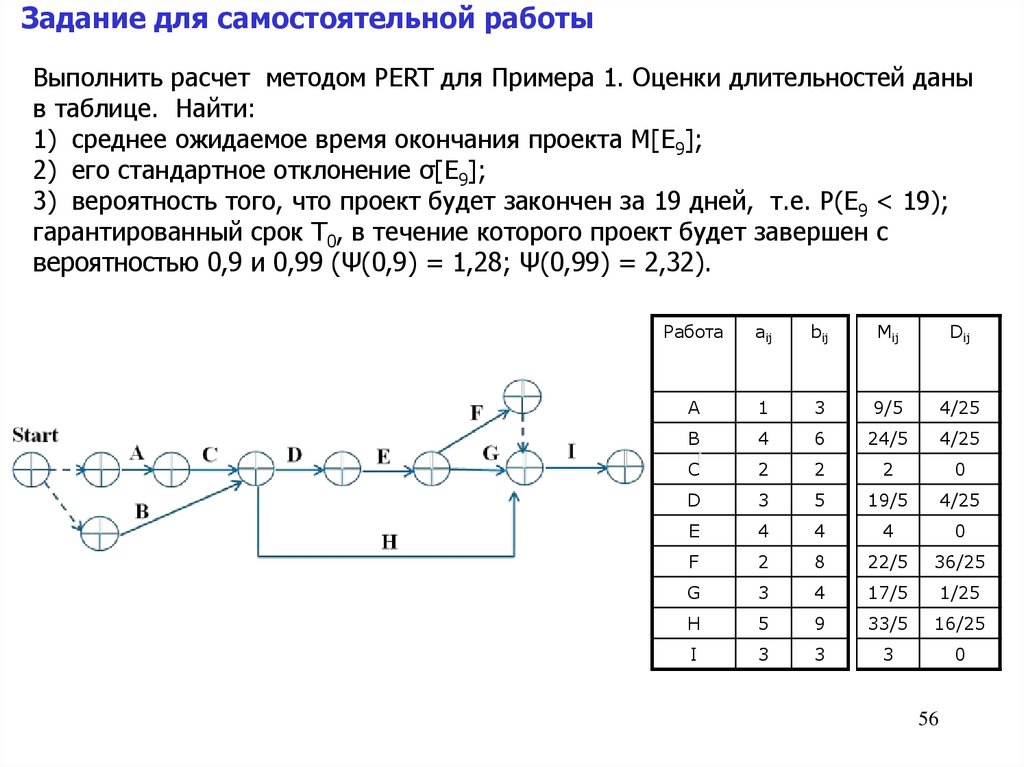
Задание для самостоятельной работыВыполнить расчет методом PERT для Примера 1. Оценки длительностей даны
в таблице. Найти:
1) среднее ожидаемое время окончания проекта M[E9];
2) его стандартное отклонение σ[E9];
3) вероятность того, что проект будет закончен за 19 дней, т.е. P(E9 < 19);
гарантированный срок T0, в течение которого проект будет завершен с
вероятностью 0,9 и 0,99 (Ψ(0,9) = 1,28; Ψ(0,99) = 2,32).
Работа
aij
bij
Mij
Dij
A
1
3
9/5
4/25
B
4
6
24/5
4/25
C
2
2
2
0
D
3
5
19/5
4/25
E
4
4
4
0
F
2
8
22/5
36/25
G
3
4
17/5
1/25
H
5
9
33/5
16/25
I
3
3
3
0
56
57.
Модель Примера 2.Start
0
1
A 5
E
7
F
B
2
H
3
4
D
6
C
8
G
9
I
10 J
Работа
aij
bij
A
2
4
B
2
2
C
4
6
D
2
5
E
4
4
F
2
2
G
3
3
H
5
9
I
3
3
J
1
4
11
Выполнить расчет методом PERT для Примера 2.
Оценки длительностей даны в таблице. Найти:
1) среднее ожидаемое время окончания проекта M[E11];
2) его стандартное отклонение σ[E11];
3) гарантированный срок T0, в течение которого проект будет завершен с
вероятностью 0,9 (Ψ(0,9) = 1,28).
57
58.
Критика методики PERT.Классическая аналитическая методика PERT анализа проекта со случайными
длительностями работ неоднократно подвергалась критике. Лежащее в ее
основе предположение о неизменности конфигурации критических путей в
графе представляется слишком сильным.
Легко представить ситуацию, когда анализируемая k-я вершина связана с
начальной несколькими путями, почти одинаковыми по длине. Тогда
случайные вариации длин ребер могут привести к появлению новых путей,
более длинных по сравнению с путем в «усредненном» графе. По этой
причине методика PERT дает заниженные значения средних ожидаемых
моментов времени наступления событий. В частности, проведенные
Д.И. Голенко эксперименты показали, что гарантированное время
выполнения проекта в целом, вычисленное по формуле Tk P M Ek P Ek
при различных P, на 15–20% меньше истинной оценки, полученной с
помощью метода статистического моделирования.
58
59.
1.3. Распределение ресурсовВыше всякий проект рассматривался только с точки зрения времени, не
обращая внимание на ресурсы, другими словами, предполагали ресурсы
неограниченными.
Однако на практике именно недостаток ресурсов является причиной
невозможности выполнить проект за минимально возможное время. В связи
с этим задача управления ресурсами является одной из ключевых
в управлении проектами.
Задача распределения ресурсов в проекте отнюдь не тривиальная по крайней
мере по трем причинам:
1. Каждая работа может требовать много различных видов ресурсов:
трудовых, материальных, энергетических, финансовых. Трудовые ресурсы
различаются специализацией исполнителей, для разных работ требуется
разное оборудование, при этом возможна конкуренция нескольких работ
за дефицитные или уникальные ресурсы.
2. Оптимизация распределения ресурсов может осуществляться по
различным критериям. В качестве целевой функции могут выступать
время выполнения проекта или его стоимость. Кроме того, существуют
разнообразные дополнительные ограничения на календарный график.
59
60.
3. Каждый вид ресурса имеет особенности его потребления. Укажем тольконекоторые из них:
возобновляемость. Все ресурсы делятся на возобновляемые (renewable),
т. е. постоянно имеющиеся в наличии независимо от того, потребляются они
или нет, и невозобновляемые (nonrenewable);
складируемость;
доступность по календарю. Обычно возобновляемые ресурсы доступны
только в соответствии с заранее установленным календарем. Он может быть
как стандартным для всего проекта (начало и конец рабочего дня, выходные,
праздники), так и индивидуальным для данного ресурса;
равномерность потребления. Некоторые возобновляемые ресурсы
целесообразно загружать равномерно во времени. Это относится прежде всего
к трудовым ресурсам, так как зарплату штатному работнику приходится
платить независимо от его загрузки.
60
61.
По указанным выше причинам проблема календарного планирования ресурсов не имеетобщего решения. Более того, даже простые с виду попытки оптимального управления
ресурсами при их строгой формализации приводят к чрезвычайно трудно решаемым
задачам дискретного математического программирования.
Реализованные в пакетах управления проектами алгоритмы рассчитаны на самые
простые случаи и являются эвристическими, дающими приближенное, но приемлемое
на практике решение. Классической постановкой задачи календарного планирования
считается выравнивание (leveling) ресурсов, при которой ситуации превышения
доступного уровня устраняются путем переноса сроков выполнения работ, при этом
общее время выполнения проекта, как правило, увеличивается, однако при удачном
стечении обстоятельств может остаться неизменным.
Алгоритмы выравнивания ресурсов подразделяются на две группы:
параллельные
последовательные.
При параллельном планировании допускается прерывание однажды начатой работы.
При нехватке ресурсов она приостанавливается и вновь запускается при появлении
освободившихся от других работ ресурсов. При последовательном планировании
прерывать начатую работу нельзя до ее окончания.
Разумеется, параллельные алгоритмы дают большую свободу действий, однако при
этом возможны потери времени и денег при каждой переброске ресурсов
на другую работу.
61
62.
Пример 8.В Примере 4 будем считать, что для выполнения перечисленных в исходной
таблице работ требуется не только время, но и единственный вид трудовых
ресурсов — рабочие. При этом предполагаем, что рабочие обладают
универсальными навыками и могут исполнять любую работу, если имеется
достаточное их число.
Пусть объем доступного ресурса (число рабочих) в каждый момент времени
постоянен и равен V = 3. Спрашивается, можно ли в таких условиях выполнить
проект за минимальные 25 дней?
62
63.
6364.
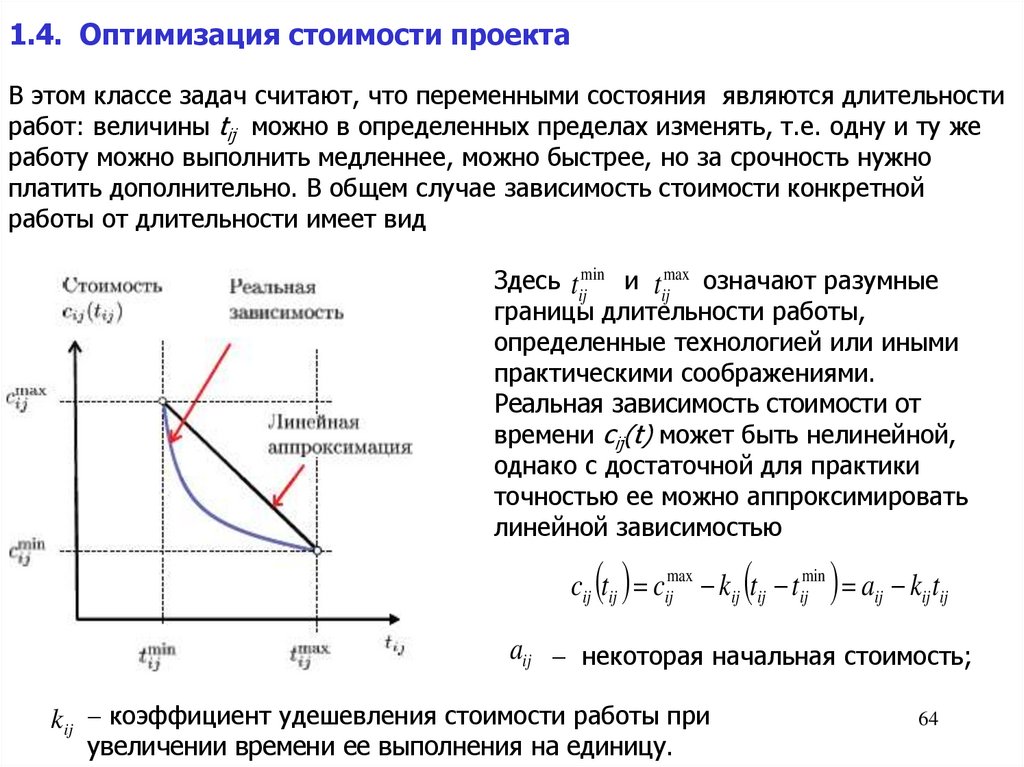
1.4. Оптимизация стоимости проектаВ этом классе задач считают, что переменными состояния являются длительности
работ: величины tij можно в определенных пределах изменять, т.е. одну и ту же
работу можно выполнить медленнее, можно быстрее, но за срочность нужно
платить дополнительно. В общем случае зависимость стоимости конкретной
работы от длительности имеет вид
Здесь tijmin и tijmax означают разумные
границы длительности работы,
определенные технологией или иными
практическими соображениями.
Реальная зависимость стоимости от
времени cij(t) может быть нелинейной,
однако с достаточной для практики
точностью ее можно аппроксимировать
линейной зависимостью
cij tij cijmax kij tij tijmin aij kij tij
aij некоторая начальная стоимость;
kij коэффициент удешевления стоимости работы при
увеличении времени ее выполнения на единицу.
64
65.
Если известны минимальные и максимальные продолжительности каждойработы, нужно рассчитать сетевую модель проекта в двух вариантах:
форсированном: у каждой работы tij tijmin ;
ленивом: у каждой работы tij tij ,
max
и для каждого из них определить критическое время проекта: Tmin и Tmax.
Идея минимизации стоимости проекта состоит в том, чтобы, использовав
пропадающие впустую свободные резервы времени, растянуть сроки
выполнения работ и тем самым уменьшить их стоимость; это образно можно
понимать как «торговлю свободным временем».
Задачу об оптимизации стоимости можно поставить как:
минимизацию прямых затрат при ограничении времени выполнения
проекта;
минимизацию полных затрат.
65
66.
1.4.1. Минимизация прямых затратПод прямыми затратами (direct costs) понимаются затраты, идущие
непосредственно на выполнение работ проекта (зарплата исполнителей,
стоимость ресурсов / оборудования).
Величина прямых затрат равна:
Fm cij aij kijtij Fm 0 kijtij min
( i , j ) U
( i , j ) U
( i , j ) U
где Fm0 — постоянное слагаемое , которое не зависит от оптимизируемых
переменных, оно задает некоторую начальную точку отсчета стоимости, но
определяется конкретной экономической задачей,
поскольку требует знания
max
максимальной стоимости каждой работы cij .
В формальной постановке Fm0 можно опустить, т.к. постоянное значение в
целевой функции не влияет на оптимальное решение.
Если время выполнения проекта не ограничивать, то задача минимизации
величины прямых затрат по переменным tij имеет тривиальное решение: время
max
выполнения всех работ следует установить максимально возможным: tij tij .
66
67.
В реальности время выполнения проекта имеет ограничение: весь проектдолжен уложиться в нормативный срок T, находящийся в границах [Tmin, Tmax],
и который задает ЛПР.
В этом случае имеет место следующая постановка задачи:
1. Переменные состояния, полностью определяющие сетевую модель:
Ti — время наступления события i (i = 0, . . . , n), где n — номер события,
соответствующего концу проекта;
tij — длительность работы (i, j); число этих переменных равно
количеству реальных работ.
2. Целевая функция
Целевую функцию, соответствующую прямым затратам можно упростить, опустив
постоянное слагаемое и избавившись от отрицательных значений путем
смены направления оптимизации. В итоге имеем
Fm kij tij max
( i , j ) U
67
68.
3. Ограничения задачи делятся на несколько групп:а) tijmin tij tijmax - в общем случае для всех реальных работ, а в частности
tij tijmin tijmax
- для работ с постоянной длительностью. Такую переменную
можно рассматривать как параметр;
б) T j Ti tij , где (i, j) ∈ U. Ограничения этой группы непосредственно задают
сетевую модель, их количество для события j равно числу дуг, входящих в это
событие, включая дуги, соответствующие фиктивным работам. Таким образом,
число таких ограничений соответствует числу всех дуг сетевой модели;
в) T0 0, Tn T , где T — нормативный срок выполнения проекта, выбранный ЛПР
из промежутка [Tmin, Tmax];
г) условия неотрицательности переменных состояния: Ti ≥0, tij ≥0.
Получившаяся оптимизационная задача есть задача линейного
программирования.
min max
Входящие в условия числовые коэффициенты tij , tij , kij являются
исходными данными.
Множество ребер U определяется структурой сетевой модели.
Значение параметра T задет ЛПР (менеджер проекта).
68
69.
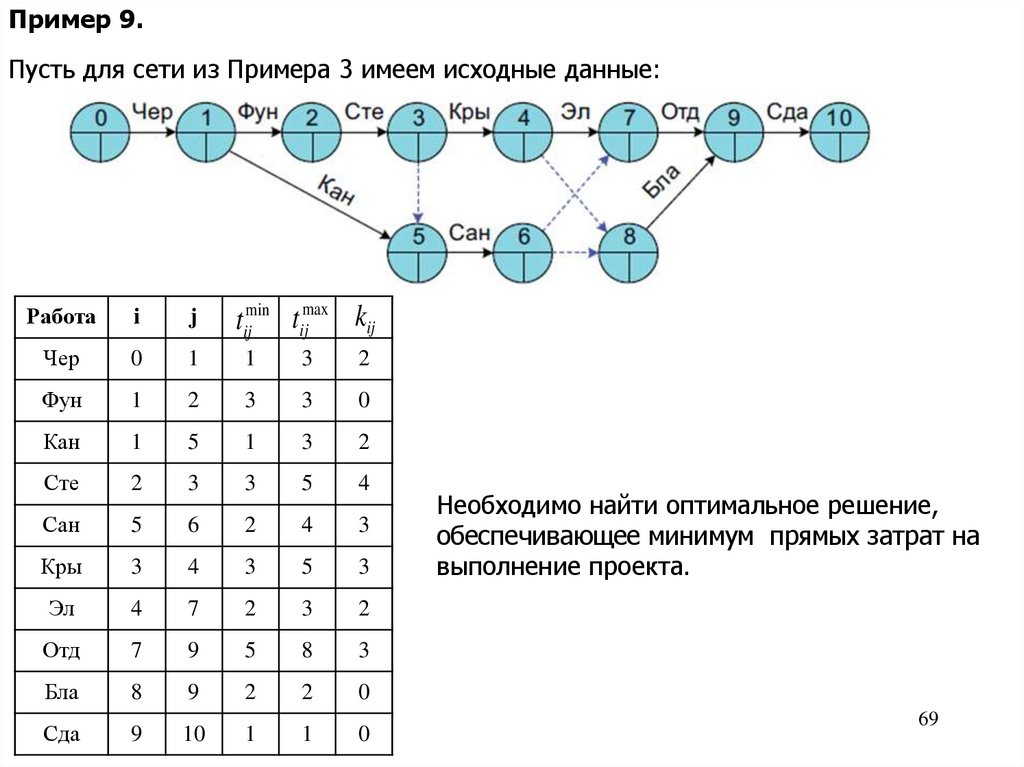
Пример 9.Пусть для сети из Примера 3 имеем исходные данные:
Работа
i
j
tijmin tijmax kij
Чер
0
1
1
3
2
Фун
1
2
3
3
0
Кан
1
5
1
3
2
Сте
2
3
3
5
4
Сан
5
6
2
4
3
Кры
3
4
3
5
3
Эл
4
7
2
3
2
Отд
7
9
5
8
3
Бла
8
9
2
2
0
Сда
9
10
1
1
0
Необходимо найти оптимальное решение,
обеспечивающее минимум прямых затрат на
выполнение проекта.
69
70.
Первоначально, используя прямой проход метода СРМ, найдем длительностипроекта при форсированном и ленивом времени выполнения каждой работы.
Полученные соответствующие значения Tmin=18, Tmax =28 формируют пределы
изменения нормативного срока выполнения проекта Т [18, 28].
(Справедливость данных значений проверить самостоятельно!!!)
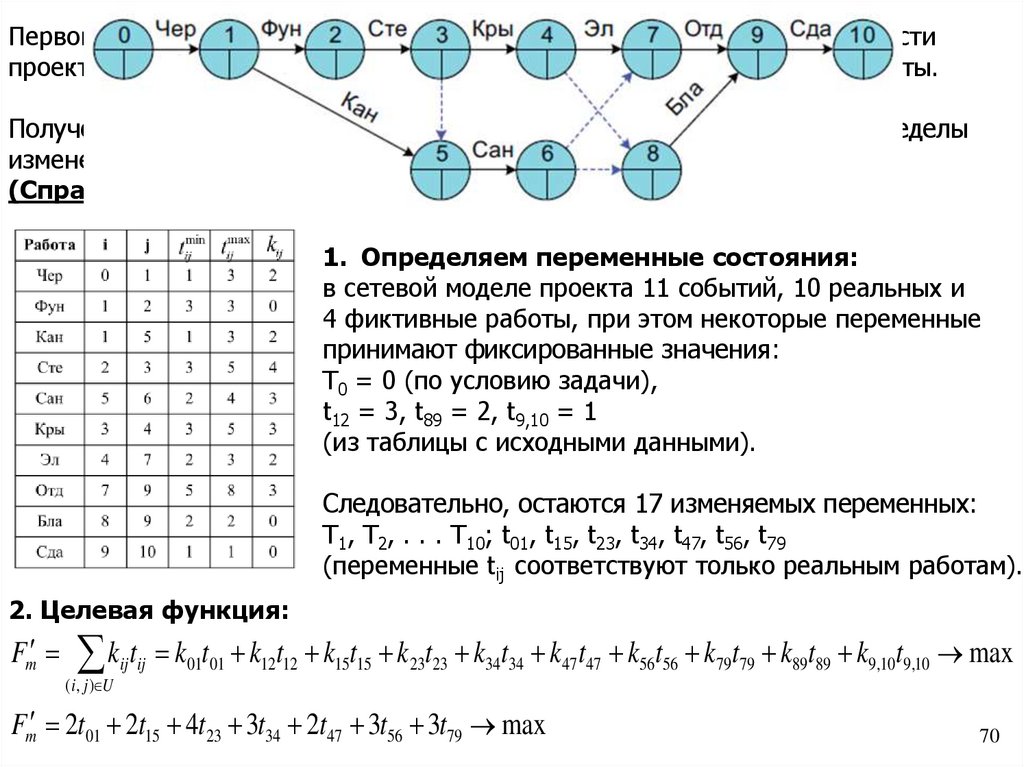
1. Определяем переменные состояния:
в сетевой моделе проекта 11 событий, 10 реальных и
4 фиктивные работы, при этом некоторые переменные
принимают фиксированные значения:
T0 = 0 (по условию задачи),
t12 = 3, t89 = 2, t9,10 = 1
(из таблицы с исходными данными).
Следовательно, остаются 17 изменяемых переменных:
T1, T2, . . . T10; t01, t15, t23, t34, t47, t56, t79
(переменные tij соответствуют только реальным работам).
2. Целевая функция:
Fm kij tij k01t01 k12t12 k15t15 k 23t23 k34t34 k 47t47 k56t56 k79t79 k89t89 k9,10t9,10 max
( i , j ) U
Fm 2t01 2t15 4t23 3t34 2t47 3t56 3t79 max
70
71.
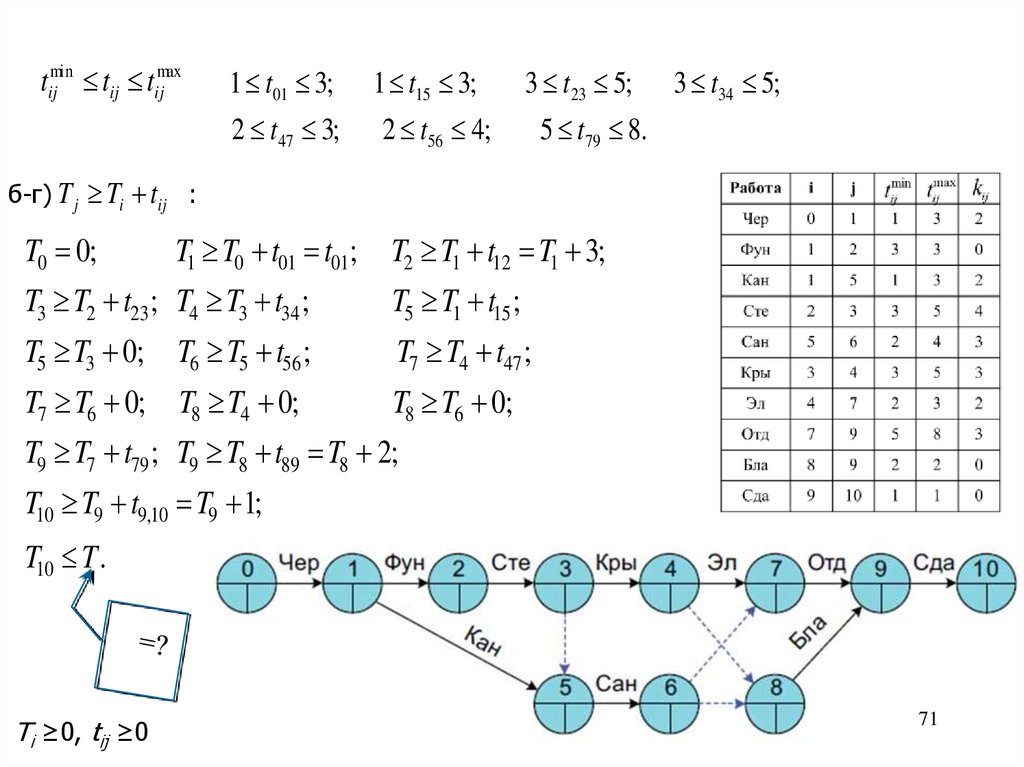
tijmin tij tijmax1 t01 3;
1 t15 3;
3 t23 5;
2 t47 3;
2 t56 4;
5 t79 8.
3 t34 5;
б-г) T j Ti tij :
T0 0;
T1 T0 t01 t01;
T2 T1 t12 T1 3;
T3 T2 t23 ; T4 T3 t34 ;
T5 T1 t15 ;
T5 T3 0;
T6 T5 t56 ;
T7 T4 t47 ;
T7 T6 0;
T8 T4 0;
T8 T6 0;
T9 T7 t79 ; T9 T8 t89 T8 2;
T10 T9 t9,10 T9 1;
T10 T .
Ti ≥0, tij ≥0
71
72.
В итоге имеем задачу линейного программирования. Если задаться конкретнымзначением параметра T, то эту задачу можно решить обычным симплекс-методом.
Приняв Т=22, получаем Fm 74 при
t01 = 1, t15 = 3, t23 = 5, t34 = 5, t47 = 2, t56 = 4, t79 = 5;
T1 = 1, T2 = 4, T3 = 9, T4 = 14, T5 = 9, T6 = 13, T7 = 16, T8 = 14, T9 = 21, T10 = 22.
Т
F’m
18
60
20
68
22
74
24
80
26
85
28
89
72
73.
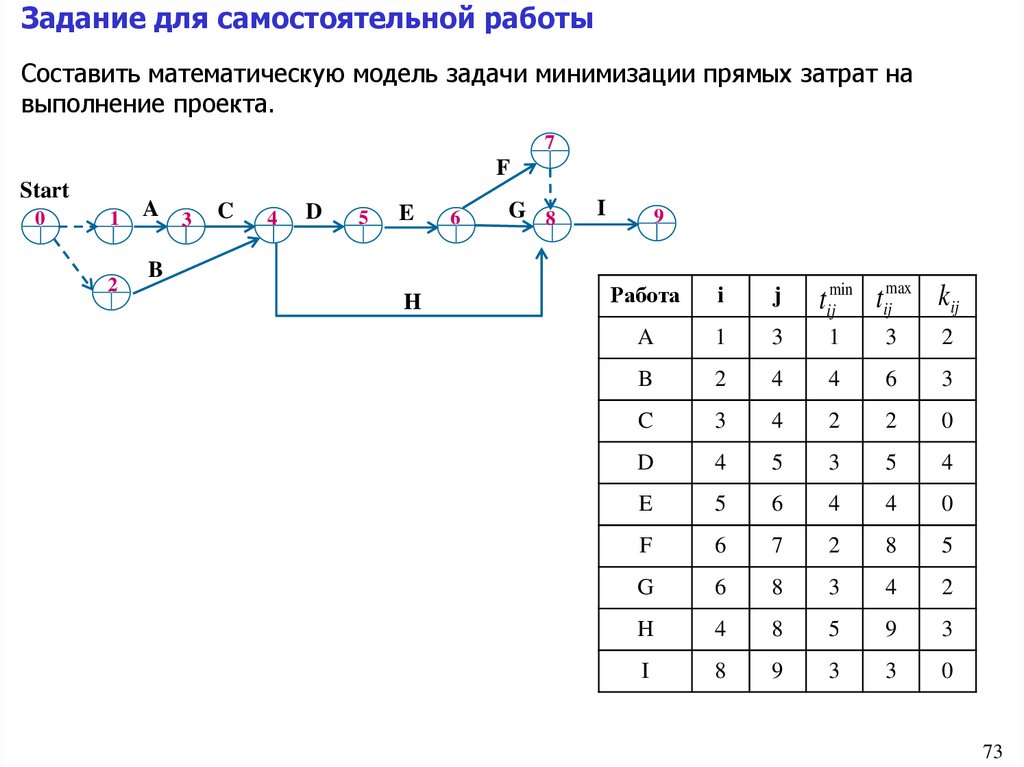
Задание для самостоятельной работыСоставить математическую модель задачи минимизации прямых затрат на
выполнение проекта.
7
F
Start
0
1
2
A
3
C
4
D
5
E
6
G 8
I
9
B
H
Работа
i
j
tijmin tijmax kij
A
1
3
1
3
2
B
2
4
4
6
3
C
3
4
2
2
0
D
4
5
3
5
4
E
5
6
4
4
0
F
6
7
2
8
5
G
6
8
3
4
2
H
4
8
5
9
3
I
8
9
3
3
0
73
74.
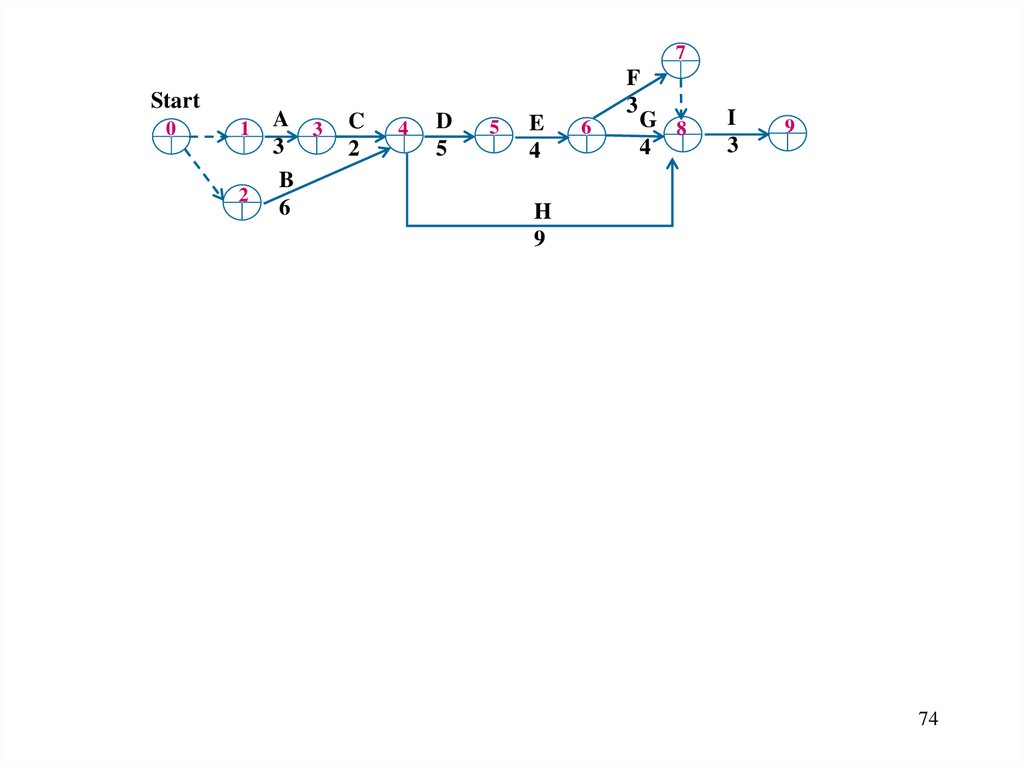
7Start
0
1
2
A 3
3
B
6
C
2
4
D
5
5
E
4
6
F
3
G 8
4
I
3
9
H
9
74
75.
1.4.2. Минимизация полных затратПри выполнении реального проекта кроме прямых затрат приходится нести
затраты, связанные с поддержанием проекта в целом. Например, при
строительстве дома нужно постоянно платить за аренду техники, охрану,
содержание вспомогательного персонала и т. п.
С определенной долей условности эти косвенные расходы (обозначим их q) можно
считать постоянными во времени, тогда их величина будет линейно возрастать с
увеличением длительности проекта T. Складывая их с прямыми, мы получаем
ситуацию, когда прямые и косвенные затраты, имея противоположные
тенденции изменения, формируют функцию полных затрат, имеющую выраженный
минимум. Соответствующая этому минимуму длительность проекта T∗ является
оптимальной.
Ff cij qTn aij kijtij qTn Fm 0 kijtij qTn min
( i , j ) U
( i , j ) U
( i , j ) U
F f kij tij qTn max
( i , j ) U
tijmin tij tijmax
T j Ti tij
T0 0
75
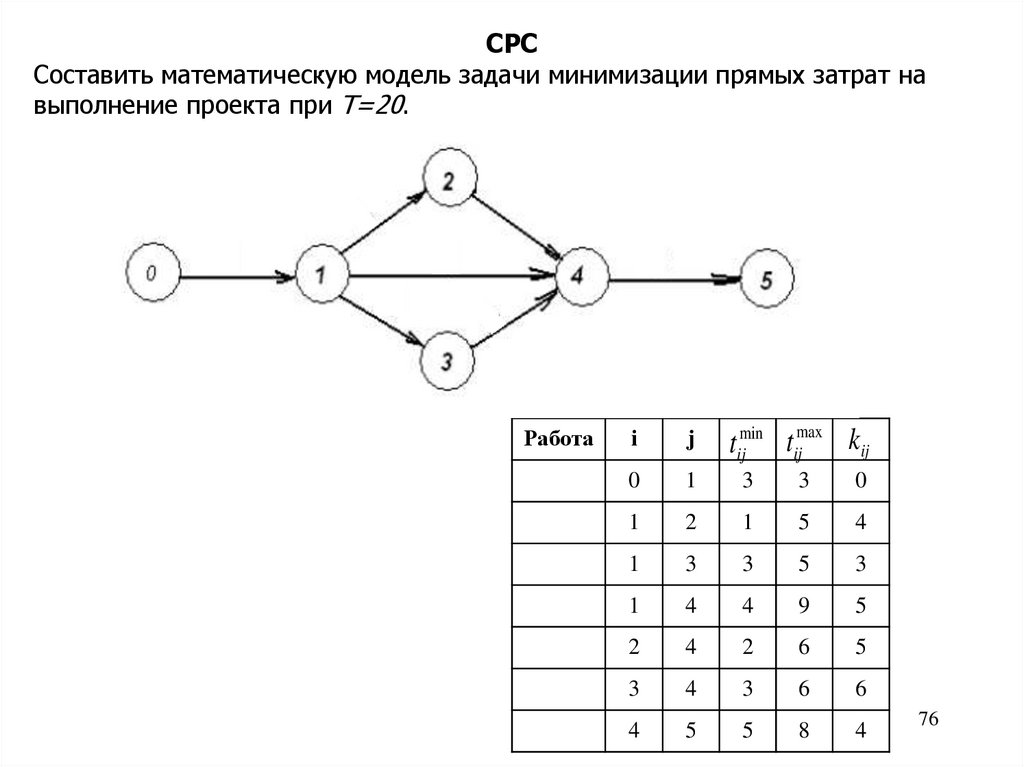
76.
СРССоставить математическую модель задачи минимизации прямых затрат на
выполнение проекта при T=20.
Работа
i
j
tijmin tijmax kij
0
1
3
3
0
1
2
1
5
4
1
3
3
5
3
1
4
4
9
5
2
4
2
6
5
3
4
3
6
6
4
5
5
8
4
76
77.
Полный учебный курс по MS Project2013 (Владимир Иванов)
http://www.youtube.com/playlist?list=PL3L1fFlpk8EBzvdeREAildlM9-CDg7tFX
77















































 Программное обеспечение
Программное обеспечение








