Требования к вычислительным алгоритмам

1.

ТРЕБОВАНИЯ К ВЫЧИСЛИТЕЛЬНЫМ АЛГОРИТМАМ
Вычислительный метод, доведенный до степени детализации, позволяющий
реализовать его на ЭВМ, принимает форму вычислительного алгоритма.
Определим вычислительный алгоритм как точное предписание действий
над входными данными, задающее вычислительный процесс, направленный на
преобразование произвольных входных данных х (из множества допустимых
для данного алгоритма входных данных X) в полностью определяемый этими
входными данными результат.
Реальный вычислительный алгоритм складывается из двух частей:
абстрактного
вычислительного
алгоритма,
формулируемого
в
общепринятых математических терминах, и программы, записанной на одном
из алгоритмических языков и предназначенной для реализации алгоритма на
ЭВМ. К вычислительным алгоритмам, предназначенным для широкого
использования, предъявляется ряд весьма жестких требований. Первое из них
— корректность алгоритма.
Будем называть вычислительный алгоритм корректным, если выполнены три
условия: 1) он позволяет после выполнения конечного числа элементарных для
вычислительной машины операций преобразовать любое входное данное х Х
в результат у; 2) результат у устойчив по отношению к малым возмущениям
входных данных;
3) результат у обладает вычислительной устойчивостью. Если хотя бы одно
из перечисленных условий не выполнено, то будем называть алгоритм
некорректным. Уточним и более подробно обсудим эти условия.
1

2.

Необходимость выполнения первого условия понятна. Если для получения
результата нужно выполнить бесконечное число операций либо требуются
операции, не реализованные на ЭВМ, то алгоритм следует признать
некорректным.
Устойчивость по входным данным. Устойчивость результата у к малым
возмущениям входных данных (устойчивость по входным данным) означает, что
результат непрерывным образом зависит от входных данных при условии, что
отсутствует вычислительная погрешность.
Это требование устойчивости аналогично требованию устойчивости
вычислительной задачи. Отсутствие такой устойчивости делает алгоритм
непригодным для использования на практике.
Отметим, что в формулировку устойчивости алгоритма по входным данным
неявно входит одно важное предположение, а именно, что вместе с входным
данным х в множество допустимых входных данных X входят и все близкие к х
приближенные входные данные х*.
Вычислительная устойчивость. Из-за наличия ошибок округления при
вводе входных данных в ЭВМ и при выполнении арифметических операций
неизбежно появление вычислительной погрешности.
Ее величина на разных ЭВМ различна из-за различий в разрядности и
способах округления, но для фиксированного алгоритма в основном величина
погрешности определяется машинной точностью м.
Назовем алгоритм вычислительно устойчивым, если вычислительная
погрешность результата стремится к нулю при м 0.
2

3.

Обычно вычислительный алгоритм называют устойчивым, если он устойчив
по входным данным и вычислительно устойчив, и неустойчивым, если хотя бы
одно из этих условий не выполнено.
Вычислительная неустойчивость алгоритма часто может быть выявлена
благодаря анализу устойчивости по входным данным, так как неустойчивость к
малым ошибкам округления входных данных автоматически свидетельствует о
вычислительной неустойчивости алгоритма.
Пример 1.1. Предположим, что величины уn для n = 1, 2, ... вычисляются по
рекуррентной формуле
yn = n yn-1 + n ,
(1.1)
а величина y0 задана. Пусть y*0 — заданное приближенное значение
величины y0. Тогда (если вычисления ведутся абсолютно точно) определяемые
по формуле (1.1) приближенные значения содержат ошибки, связанные
равенством yn – y*n = n (yn-1 – y*n-1).
Следовательно, (y*n) = | n | (y*n-1) и при выполнении условия | n | < 1
алгоритм устойчив по входным данным, поскольку (y*n) < (y*0) для всех n.
Если же | n | q > 1, то (y*n) > qn (y*0) и абсолютная погрешность
неограниченно возрастает при n . В этом случае алгоритм неустойчив по
входным данным, а поэтому и вычислительно неустойчив.
Следует заметить, что алгоритм (1.1) был признан нами неустойчивым в случае
| n | q > 1 при выполнении двух условий, на которых не было достаточно
акцентировано внимание.
3

4.

Первое
из
них
состоит
в
предположении
о
неограниченной
продолжительности вычислительного процесса (n ), что невозможно на
практике. В действительности такой характер неустойчивости говорит о
тенденции к неограниченному росту погрешности при неограниченном
продолжении вычислений.
Если ошибки растут очень быстро, то вычисления могут довольно скоро
завершиться аварийным остановом по переполнению. Второе условие касается
выбранной меры погрешности.
Совсем не обязательно, чтобы рост абсолютной погрешности всегда был
неприемлем в конкретных вычислениях. Если он сопровождается сильным
ростом точного решения и при этом относительная погрешность остается малой,
то алгоритм можно признать относительно устойчивым.
Иногда короткая последовательность вычислений приводит от исходных
данных, известных с высокой точностью, к результату, содержащему
недопустимо мало верных цифр или вообще не имеющему ни одной верной
цифры. В этом случае принято говорить о катастрофической потере
точности.
Понятие обусловленности вычислительного алгоритма, отражает
чувствительность результата работы алгоритма к малым, но неизбежным
ошибкам округления.
Вычислительно устойчивый алгоритм называют хорошо обусловленным, если
малые относительные погрешности округления м приводят к малой
относительной вычислительной погрешности (у*) результата у*, и плохо
обусловленным, если вычислительная погрешность может быть недопустимо
большой.
4

5.

Если (у*) и м связаны неравенством (у*) А м , то число А следует
называть числом обусловленности вычислительного алгоритма. Для
плохо обусловленного алгоритма А >> 1.
При очень большом значении числа обусловленности алгоритм можно считать
практически неустойчивым.
Если алгоритм, предназначенный для решения хорошо обусловленной
задачи, оказался плохо обусловленным, то его следует признать
неудовлетворительным и попытаться построить более качественный алгоритм.
Для плохо обусловленных задач дело обстоит иначе. Ключ к пониманию дает
следующее высказывание: "Если задача плохо обусловлена, то никакие усилия,
потраченные на организацию изощренных вычислений, не могут дать
правильных ответов, исключая случайности" Здесь требуется серьезное
переосмысление постановки вычислительной задачи.
Различные подходы к анализу ошибок
Прямой анализ ошибок. Общий эффект влияния ошибок обычно учитывают
следующим образом. Изучают воздействие ошибок входных данных, метода и
округлений на получаемый результат у* и пытаются оценить некоторую меру
близости у* к истинному решению у.
Такой метод исследования называют прямым анализом ошибок. В
большинстве случаев мы будем следовать этому традиционному пути. Во
многих (но не во всех) случаях оценки погрешности удается получить; однако
часто они оказываются сильно завышенными и приводят к неоправданному
пессимизму в оценке качества приближенного решения.
5

6.

Реальная величина погрешности у - у* часто значительно меньше, чем ее
оценка, рассчитанная на самый неблагоприятный случай и выведенная с
помощью прямого анализа. Особенно трудным является прямой анализ
вычислительной погрешности.
Обратный анализ ошибок. В последнее время получил широкое
распространение другой подход к оценке влияния ошибок. Оказывается, что
довольно часто приближенное решение у* можно трактовать как точное
решение той же задачи, но отвечающее возмущенным исходным данным х*.
Оценка величины такого эквивалентного возмущения и является целью
обратного анализа ошибок.
В прикладных задачах входные данные, как правило, содержат погрешности.
Обратный анализ показывает, что ошибки, внесенные в решение в процессе его
вычисления, оказываются равносильными некоторым дополнительным
ошибкам, внесенным во входные данные.
Сопоставление величины эквивалентного возмущения и уровня ошибок
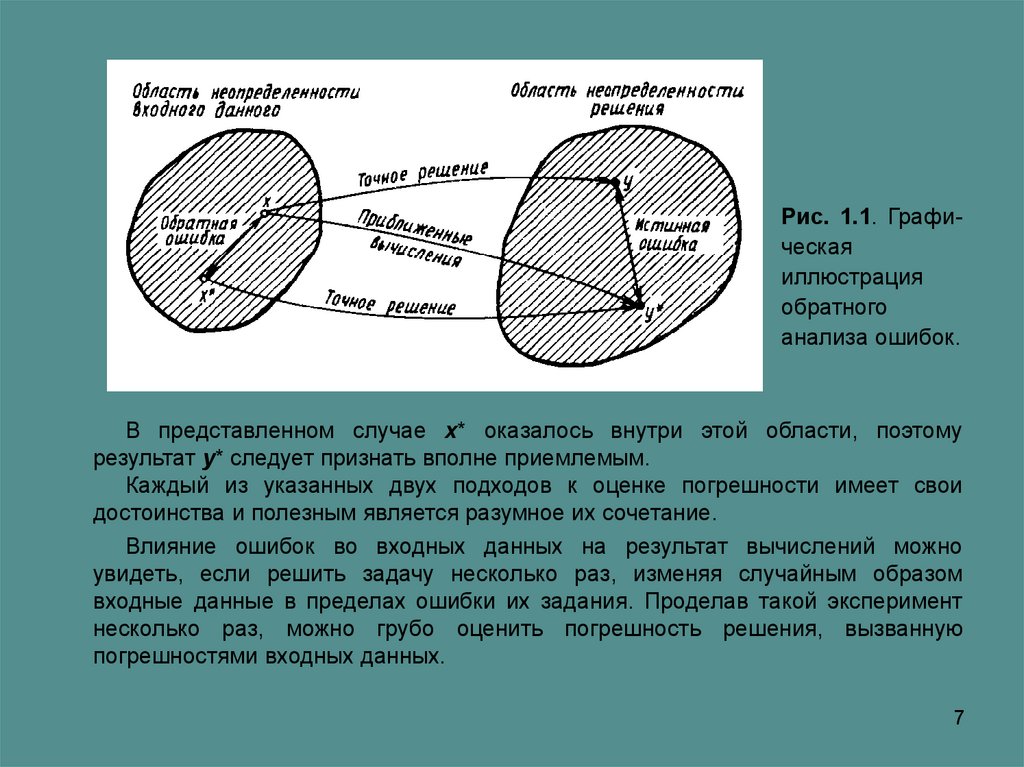
входных данных позволяет судить о качестве найденного решения. На рис. 1.1
представлена графическая иллюстрация обратного анализа ошибок.
Здесь данное х* таково, что решением задачи, соответствующим х*, является
у* — результат приближенного решения задачи с входным данным х. На рисунке
заштрихована область неопределенности входного данного; в пределах этой
области входные данные для решающего задачу неразличимы.
6

7.

Рис. 1.1. Графическая
иллюстрация
обратного
анализа ошибок.
В представленном случае х* оказалось внутри этой области, поэтому
результат у* следует признать вполне приемлемым.
Каждый из указанных двух подходов к оценке погрешности имеет свои
достоинства и полезным является разумное их сочетание.
Влияние ошибок во входных данных на результат вычислений можно
увидеть, если решить задачу несколько раз, изменяя случайным образом
входные данные в пределах ошибки их задания. Проделав такой эксперимент
несколько раз, можно грубо оценить погрешность решения, вызванную
погрешностями входных данных.
7