Похожие презентации:
Высокоточные вычисления. Компьютерная арифметика
1. Кафедра Вычислительных машин систем и сетей
Московский энергетический институтКафедра Вычислительных машин систем и сетей
КУРС ПРОБЛЕМЫ ОРГАНИЗАЦИИ ВЫЧИСЛЕНИЙ
Лекция на тему :
«Высокоточные вычисления»
Москва 2019 г.
2.
Направления по курсу ПОВ1.
«Высокоточные компьютерные арифметики» (д.т.н., Оцоков Ш.А)
2.
Машинное обучение (д.т.н., проф. Дзегеленок И.И., д.т.н., Оцоков Ш.А)
3.
Геометрическое моделирования (к.т.н., Орлов Д.А.)
4.
Технология виртуальной реальности (к.т.н., Харитонов В.Ю)
Паблик в соц сети: http://vk.com/club50059448
2
3.
Компьютерная арифметика3
4.
Требования к системам счисления«возможность представления чисел в заданном диапазоне
однозначность представления
простоту записи
удобство работы человека с машиной
трудоёмкость выполнения арифметических операций
экономичность системы (количество элементов, необходимых для
представления многоразрядных чисел)
• удобство аппаратной реализации
4
5.
Экономичная система счисления5
6.
67.
Сетунь – первый в мире троичный компьютер7
8.
89.
910.
1011.
1112.
1213.
1314.
1415.
1516. Особенности формата с плавающей точкой
3Особенности формата с плавающей точкой
последствия
Формат с плавающей точкой
Неравномерное распределение чисел
с плавающей точкой
Резкая потеря точности при
вычислениях с
разномасштабными величинами
Значения математических
эквивалентных выражений
могут быть не равными друг
другу (вычислительные
аномалии)
Нарушение законов алгебры
(коммутативности,
дистрибутивности и др.)
x ≠ (х+х)-х
…
…
…
16
17.
Нарушение законов алгебры17
18.
Недостатки формата с плавающей точкой1.
Числа с плавающей точки дают различные результаты на
различных аппаратных платформах.
2.
Сложность использования численных методов (требуются
экспертные знания в области Error Analyze)
3.
Резкий рост времени вычислений при увеличении точности
4.
В формате с плавающей точкой скрыты ошибки переполнения,
исчезновения порядка ( на флаги процессора никто не смотрит)
Пример ошибки при сложении чисел в формате с плавающей точкой:
18
19. Пример нарушения алгебраического свойства ассоциативности
(a b) c a (b c)сложение чисел с плавающей точкой
q 2,
1
1
1 1
6 6
2
2
2 2
7 6
19
20.
Неравномерное распределение чисел с плавающейточкой
(Длина мантиссы k= 3,
порядок от 0 до 4.)
Пример.
х (1017 , 1223, 1018 , 1015 , 3, - 1012 )
y (1020 , 2, 1019 , 1013 , 2111, 1016 )
Истинный результат
= 8779
Вычисленный в формате с плав. точкой один. точн.
равен 4.6E+0020.
20
21.
ПРИМЕР ЗАДАЧИ, ИМЕЮЩЕЙ РЕЗКИЙ РОСТ ОШИБОК ОКРУГЛЕНИЯМатрица Гильберта
А {ai j }, ai j
1
i j 1
Обращение матрицы Гильберта порядка 3
С точностью 2 знака после
запятой
1
прибл
А
1,17
19,51
23
23
112,94 112
112
100
19,51
1 1 / 2 1 / 3
А 1 / 2 1 / 3 1 / 4
1 / 3 1 / 4 1 / 5
Макс. относ. погрешн. более 100%.
С точностью 3 знака после
запятой
10 ,101
29 ,598
64,798
Априбл 1 41,039 192,78 202,4
34 ,6
202,4
200
Точный результат:
Aточн
1
9 36 30
36 192 180
30 180 180
Макс. относ. погрешность более 100%.
21
22.
Задачи критичные к точности компьютерных вычисленийПлохо
обусловленные
задачи с точно
заданными
исходными
данными
Задачи, которые
становятся плохо
обусловленными
при некоторых
условиях
...
Обращение
матрицы
Гильберта
Отсечение
триангуляционного
объекта,
проецируемого на
плоскость XY
Метод Эйлера
для решения
задачи Коши
Задачи
чувствительные
к изменению
шага
дискретизации
...
Задачи с
разномасштабными
коэффициентами
...
Дискретное
преобразование
Фурье с сильно
отличающимися
по величине
входными
данными
Двумерная краевая
задача для
дифференциальных
уравнений второго
порядка
Краевая задача для
нестационарного
уравнения
теплопроводности с
сильно
отличающимися
друг от друга по
величине
коэффициентами
22
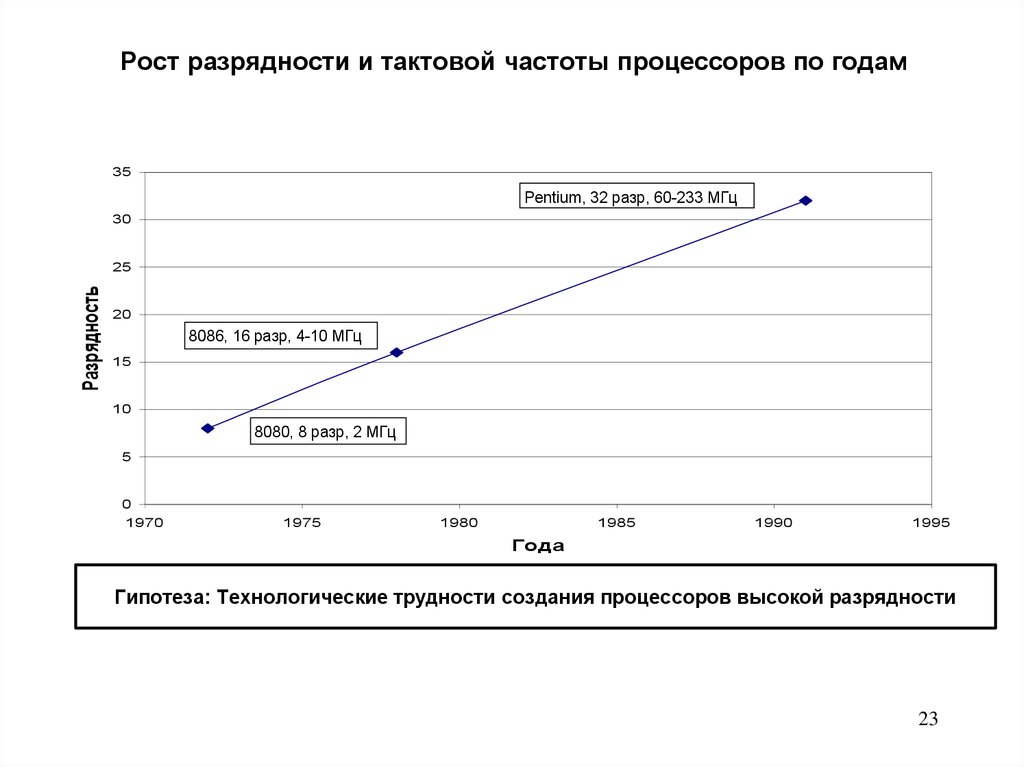
23. Рост разрядности и тактовой частоты процессоров по годам
35Pentium, 32 разр, 60-233 МГц
30
Разрядность
25
20
8086, 16 разр, 4-10 МГц
15
10
8080, 8 разр, 2 МГц
5
0
1970
1975
1980
1985
1990
1995
Года
Гипотеза: Технологические трудности создания процессоров высокой разрядности
23
24. Интервальная арифметика
Pascal XSC24
25.
Традиционный подход повышения точностивычислений
Применение библиотек высокоточных вычислений,
таких как: ZREAL(Россия), MPARITH(Германия), GMP(США)
и др.
2 nmant var
Основная проблема
Резкое увеличение времени выполнения арифметических
операций от точности. Это приводит к резкому
росту времени решения задач большой размерности.
25
26.
Подход к решению проблемы высокоточныхвычислений на основе модулярной арифметики
К настоящему времени модулярная арифметика использовалась как средство
повышения быстродействия в криптографии, нейронных сетях, цифровой обработке сигналов
и др.
Проведенные исследования показали качественно новые возможности
применения модулярной арифметики в повышении точности вычислений и ослаблении
зависимости времени вычислений от точности, для некоторых частных задач:
-
решение дифференциальных уравнений методами Рунге-Кутта,
-
нахождение скалярного произведения векторов,
-
решения систем линейных уравнений методами Гаусса-Зейделя,
-
релаксации,
-
дискретном преобразовании Фурье .
26
27.
ПРИНЦИПЫ РЕАЛИЗАЦИИ МОДУЛЯРНЫХ ВЫЧИСЛЕНИЙ27
28.
ПРИНЦИПЫ РЕАЛИЗАЦИИ МОДУЛЯРНЫХ ВЫЧИСЛЕНИЙ28
29.
ПРИНЦИПЫ РЕАЛИЗАЦИИ МОДУЛЯРНЫХ ВЫЧИСЛЕНИЙ29
30. Модулярная арифметика с дробями
3031.
Вычисления с дробями Фарея в модулярной арифметике.
31
32.
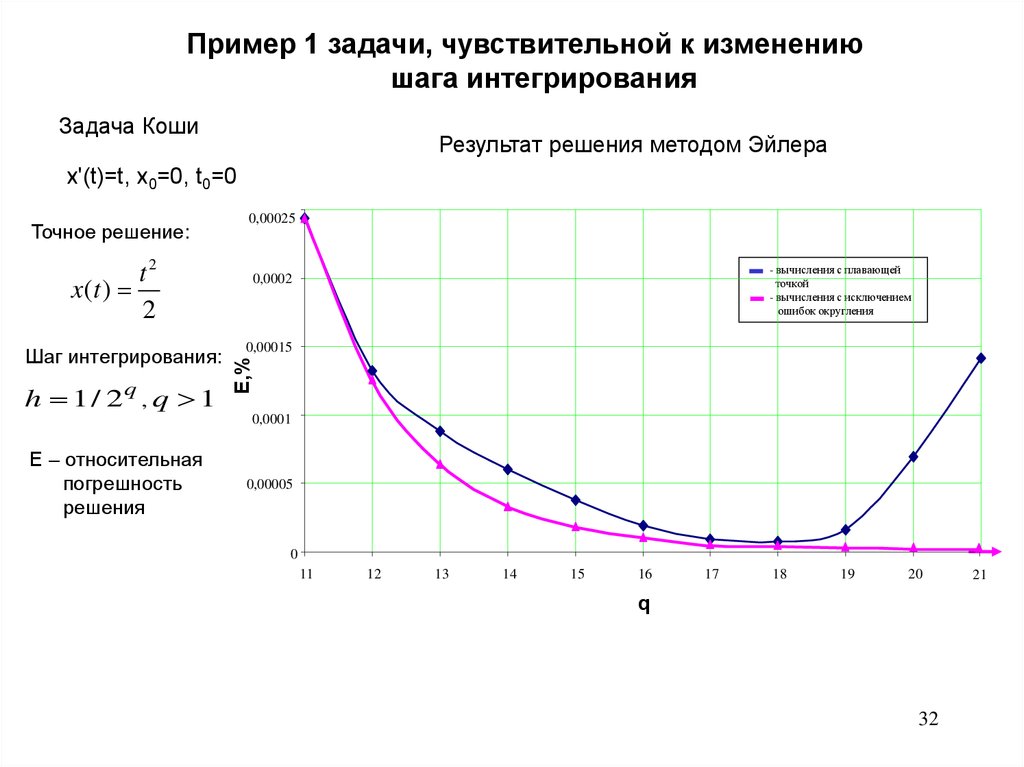
Пример 1 задачи, чувствительной к изменениюшага интегрирования
Задача Коши
Результат решения методом Эйлера
x'(t)=t, x0=0, t0=0
t2
x (t )
2
Шаг интегрирования:
h 1 / 2q , q 1
0,00025
- вычисления с плавающей
точкой
- вычисления с исключением
ошибок округления
0,0002
0,00015
E,%
Точное решение:
0,0001
E – относительная
погрешность
решения
0,00005
0
11
12
13
14
15
16
17
18
19
20
q
32
21
33.
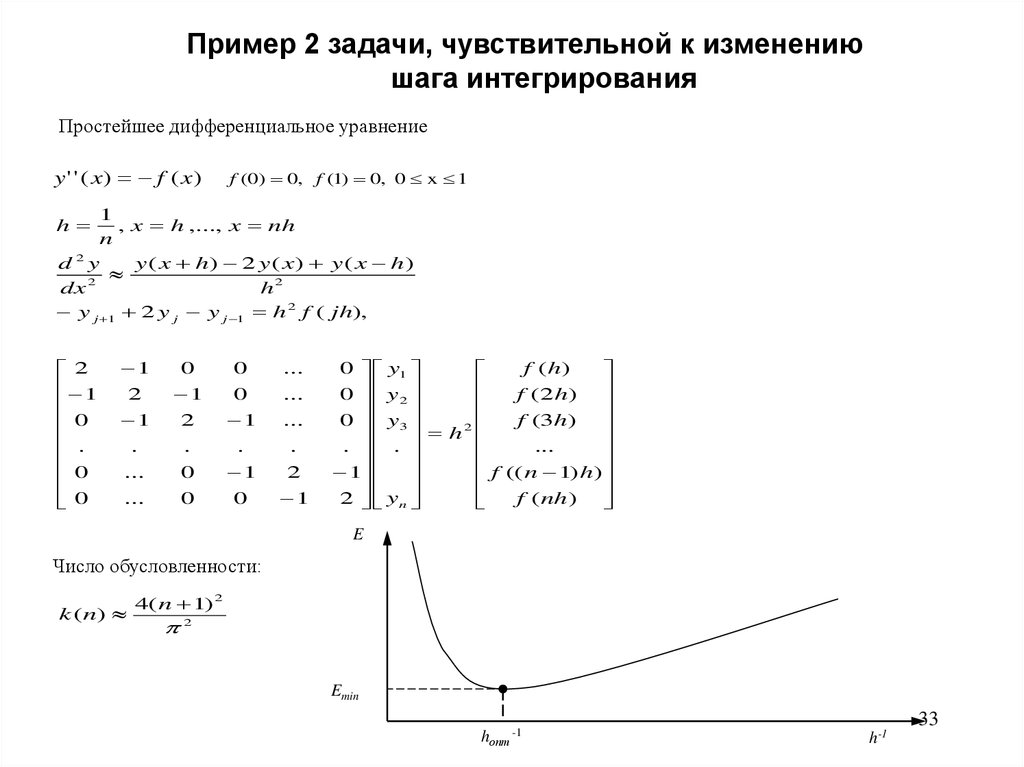
Пример 2 задачи, чувствительной к изменениюшага интегрирования
Простейшее дифференциальное уравнение
y ' ' ( x) f ( x)
f (0) 0, f (1) 0, 0 x 1
1
, x h ,..., x nh
n
d2y
y ( x h) 2 y ( x ) y ( x h)
2
dx
h2
y j 1 2 y j y j 1 h 2 f ( jh),
h
2
1
0
.
0
0
1
0
0
...
2
1
0
...
1
2
1
...
.
.
.
.
...
0
1
2
...
0
0
1
0 y1
f ( h)
0 y2
f ( 2h)
0 y3
f
(
3
h
)
2
h
. .
...
f (( n 1) h)
1
2
f ( nh)
yn
E
Число обусловленности:
k ( n)
4(n 1) 2
2
Emin
hопт -1
33
h-1
34.
ПРИМЕНЕНИЕ ВЫЧИСЛЕНИЙ С ИСКЛЮЧЕНИЕМ ОШИБОК ОКРУГЛЕНИЯВ ВЫЧИСЛИТЕЛЬНО НЕУСТОЙЧИВЫХ АЛГОРИТМАХ
Рассмотрим задачу вычисления функции ex . Известно, что эта задача хорошо обусловлена.
x
Обусловленность вычислительного алгоритма при x<0
xk
x 2 x3
xn
e
1 x
...
... .
k
!
2
!
3
!
n
!
k 0
x
e 2 x
при x<0
Пример.
Найти значение функции ex при x= -15.
Верное значение e-15 =1 / e15 0.000000305902
1. Традиционные вычисления
2. Вычисления с исключ. ошибок окр.
После выполнения 82 итераций было
После выполнения 60 итераций было
получено: e-15 0.000000256502
получено:
Относительная погрешность
составила 19,2%.
e-15
1822987410130384149007132206840681602541990778449289
59593604795584246682595675324534356863378751133750157901824
или e-15 0.000000305903159. Отн. погр. равна 0,0001%
34
35.
Оценка эффективности высокоточных вычисленийна примере нахождения скалярного произведения
Eff
T1
,
T2
- время вычислений с
использованием библиотеки
MPArith,
T1
- Tвремя
вычислений в модулярной
2
арифметике при той же точности.
35
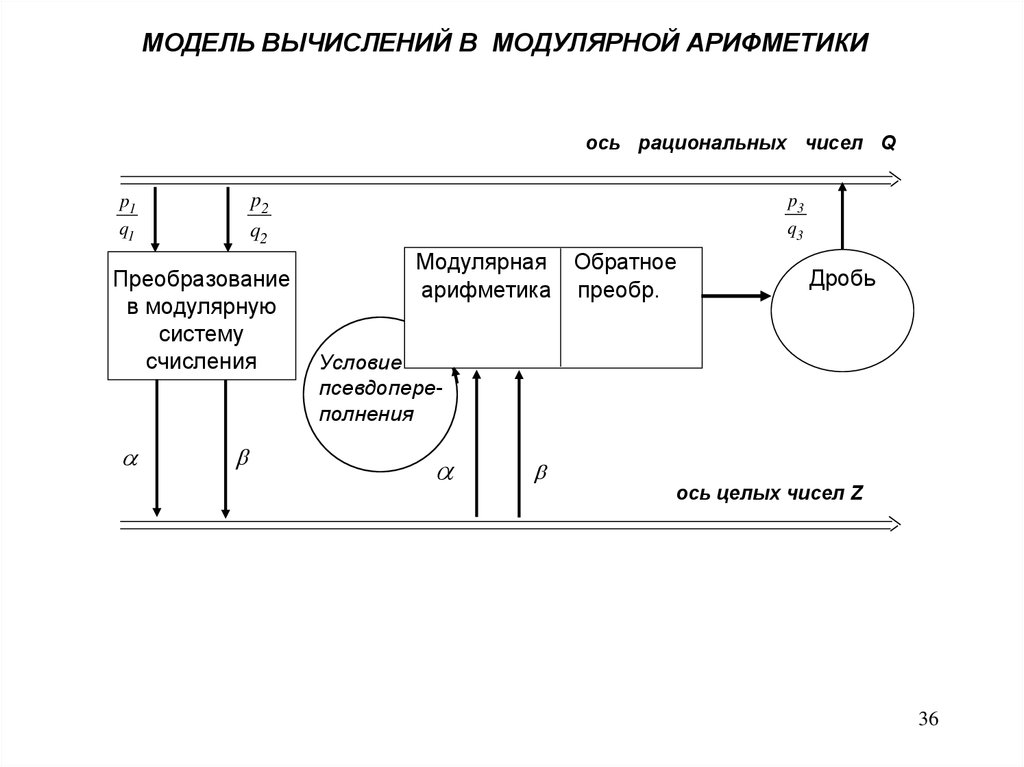
36.
МОДЕЛЬ ВЫЧИСЛЕНИЙ В МОДУЛЯРНОЙ АРИФМЕТИКИось рациональных чисел Q
p2
q2
p1
q1
Преобразование
в модулярную
систему
счисления
p3
q3
Модулярная Обратное
арифметика преобр.
Дробь
Условие
псевдопереполнения
ось целых чисел Z
36
37.
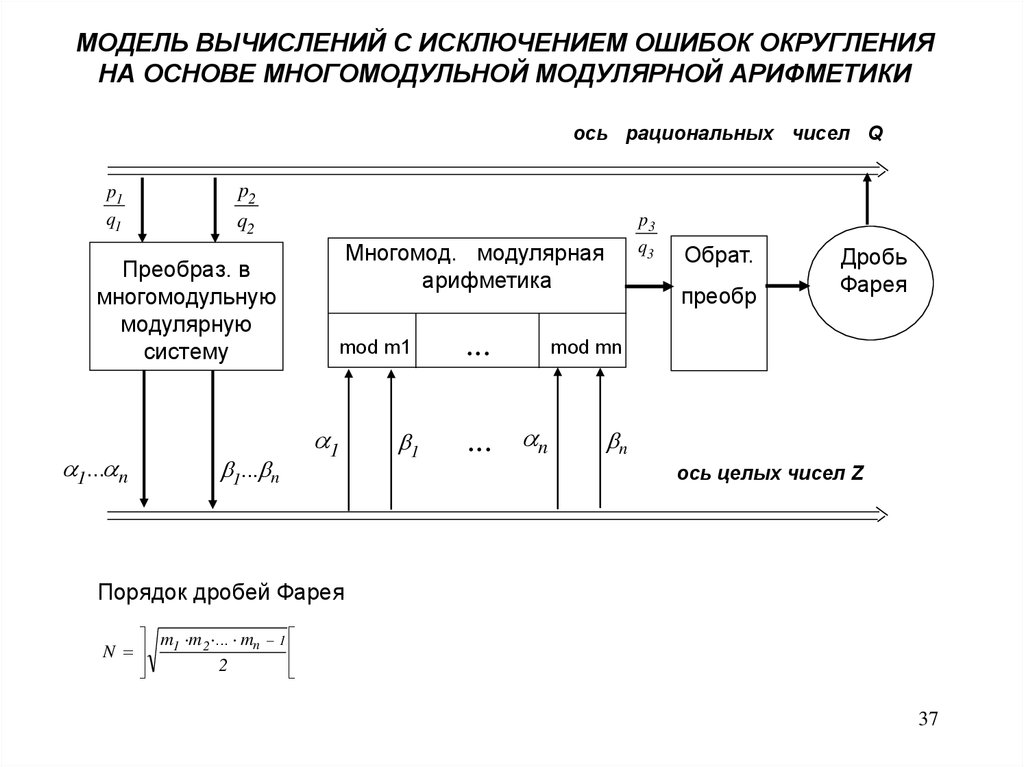
МОДЕЛЬ ВЫЧИСЛЕНИЙ С ИСКЛЮЧЕНИЕМ ОШИБОК ОКРУГЛЕНИЯНА ОСНОВЕ МНОГОМОДУЛЬНОЙ МОДУЛЯРНОЙ АРИФМЕТИКИ
ось рациональных чисел Q
p1
q1
p2
q2
Многомод. модулярная
арифметика
Преобраз. в
многомодульную
модулярную
систему
1... n
p3
q3
mod m1
1
1... n
1
...
...
Обрат.
преобр
Дробь
Фарея
mod mn
n
n
ось целых чисел Z
Порядок дробей Фарея
m m ... mn
N 1 2
2
1
37
38.
ИСХОДНЫЕ ПРИНЦИПЫ РЕАЛИЗАЦИИ МОДЕЛИПоле p-адических чисел определяется как пополнение множества рациональных
чисел по р-адической метрике, которая является неархимедовой и для нее
выполняется неравенство «равнобедренного треугольника»
Любое рациональное число имеет единственное р-адическое разложение:
a jp
j n
j
, где a
j
0 ,1 ,..., p 1 ,
p
p
n
Код Гензеля H(p,r, ) - отрезок длины r бесконечного р-адического разложения
числа .
Теорема
Пусть a c p n , ( c , d ) ( c , p ) ( d , p ) 1 .
Обозначим
(c d
1
b
d
H ( p , r , c / d ) .a 0 a 1 ... a r 1
, тогда
) mod m a 0 a 1 p a 2 p 2 ... a r 1 p r 1
где m=p r
38
39.
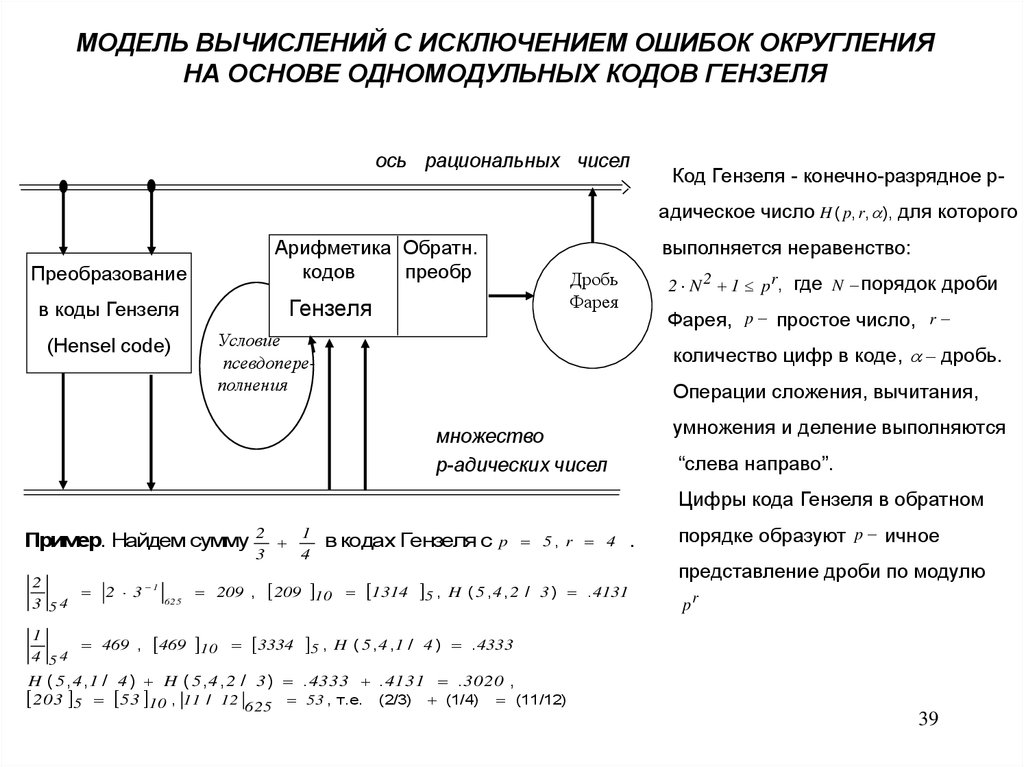
МОДЕЛЬ ВЫЧИСЛЕНИЙ С ИСКЛЮЧЕНИЕМ ОШИБОК ОКРУГЛЕНИЯНА ОСНОВЕ ОДНОМОДУЛЬНЫХ КОДОВ ГЕНЗЕЛЯ
ось рациональных чисел
Код Гензеля - конечно-разрядное радическое число H ( p, r, ), для которого
Преобразование
Дробь
Фарея
Гензеля
в коды Гензеля
(Hensel code)
выполняется неравенство:
Арифметика Обратн.
кодов
преобр
2 N 2 1 p r, где N порядок дроби
Фарея, p простое число, r
Условие
псевдопереполнения
количество цифр в коде, дробь.
Операции сложения, вычитания,
умножения и деление выполняются
множество
p-адических чисел
“слева направо”.
Цифры кода Гензеля в обратном
Пример. Найдем сумму 2
3
2
2 3 1
3 54
625
209 ,
1
4
в кодах Гензеля с
209 10
1314 5 ,
p 5, r 4
H ( 5 , 4 , 2 / 3 ) . 4131
1
469 , 469 10 3334 5 , H ( 5 , 4 ,1 / 4 ) . 4333
4 54
H ( 5 ,4 ,1 / 4 ) H ( 5 ,4 , 2 / 3 ) . 4333 . 4131 . 3020 ,
203 5 53 10 , 11 / 12 625 53 , т.е. (2/3) (1/4) (11/12)
.
порядке образуют p ичное
представление дроби по модулю
pr
39
40.
МОДЕЛЬ ПАРАЛЛЕЛЬНЫХ ВЫЧИСЛЕНИЙ С ИСКЛЮЧЕНИЕМ ОШИБОКОКРУГЛЕНИЯ НА ОСНОВЕ МНОГОМОДУЛЬНЫХ КОДОВ ГЕНЗЕЛЯ
ось рациональных чисел
с
d
a
b
Преобразование
Параллельная
Обратн.
Дробь
в многомодул. коды Гензеля с
арифметика
преобр.
Фарея
модулями и порядками
кодов Гензеля
( p 1 , r ),..., ( p k , r )
соответственно.
p1 , r
...
...
pk r
p1 , r
...
...
pk r
p1 , r
...
...
pk r
p1 , r
...
...
pk r
Условие
псевдопереполнения
множество
p-адических чисел
40
41.
ПРИМЕР ВЫЧИСЛЕНИЙ С ИСКЛЮЧЕНИЕМ ОШИБОК ОКРУГЛЕНИЯ ВМНОГОМОДУЛЬНОЙ СИСТЕМЕ ГЕНЗЕЛЯ
Найти сумму
1
1
2
3
Выберем модули
p1 5, p 2 7
, порядок r
2
Определим сумму дробей в кодах Гензеля по каждому
Сложность арифметических
операций в кодах Гензеля в
двоичной системе счисления:
модулю.
H ( 5 , 2 , 1 / 2 ) H ( 5 , 2 , 1 / 3 ) . 01
H ( 7 , 2 , 1 / 2 ) H ( 7 , 2 , 1 / 3 ) . 21
, ( 10 )
, ( 12 )
p1
( 5 ) 10
p 2
( 9 ) 10
Суммы могут вычисляться параллельно.
Применим Китайскую теорему об остатках для перевода
числа:
, : O B ( r log 2 p )
*, / : O B ( r 2 log 2 p )
Коды Гензеля могут
применяться:
(5,9) из модулярной системы по модулям (25,49) в
позиционную
Для реализации вычислений с
полиномами (полиномиальная
счисления. Вычислим ортогональные базисы по формулам:
арифметика)
1
M
Bi i
, где
mi
B 1 1176
A
, B2
M
mi
i
Для реализации вычислений с
mi
50
5 B1 9 B 2
M
плавающей точкой без ошибок
205 , 205
5
6
округления.
M
41
42.
ОЦЕНКА ЭФФЕКТИВНОСТИ ВЫЧИСЛЕНИЙ С ИСКЛЮЧЕНИЕМОШИБОК ОКРУГЛЕНИЯ, РЕАЛИЗОВАННЫХ В MAPLE
Эффективность исследовалась на примере решения системы
линейных уравнений с рациональными коэффициентами
размерностью 20
90000
Средний
коэфф.
абс.
ускорения:
80000
Maple
70000
Kабс 1,5
Время (мс)
60000
50000
Hensel
Maple
Коды Гензеля
40000
30000
20000
10000
0
5
10
15
20
Разрядность коэффициентов
25
30
42
43.
СХЕМА ОРГАНИЗАЦИИ ВЫЧИСЛЕНИЙ С ЗАДАННОЙ ТОЧНОСТЬЮИсходные
данные*:
Х
Требуемая
точность
конечных
результ.
ТЕКСТ
ПРОГРАММЫ
1. Выделение графсхемы
вычислительного
процесса
КОМПИЛЯТОР
ЯЗЫКА ВЫСОКОГО
УРОВНЯ
* Предполагается,
что исходные
данные заданы
точно.
ГРАФ-СХЕМА
ВЫЧ.
ПРОЦЕССА
ОПРЕДЕЛЕНИЕ ВЕЛ.
МОДУЛЕЙ И
КОМПИЛЯЦИЯ
ОПРЕДЕЛЕНИЕ
ДЛИНЫ
МАНТИССЫ,
ДОСТАТОЧНОЙ
ДЛЯ РЕШЕНИЯ
ЗАДАЧИ С
ТРЕБУЕМОЙ
ТОЧНОСТЬЮ
2. Анализ
распространения
ошибок округления и
определение величины
максимально возможной
относ. ошибки округления
ВЫПОЛНЕНИЕ ПРОГРАММЫ
НА ПРОЦЕССОРЕ, ФУНКЦ. В
МОДУЛЯРНОЙ СИСТЕМЕ
СЧИСЛЕНИЯ
Результат:
Y
с требуемой
точностью
43
44.
ФОРМУЛЫ ОТНОСИТЕЛЬНЫХ ОШИБОК ОКРУГЛЕНИЯПусть имеются два приближения x, y к двум величинам x, y и ex , e y - соответствующие абсолютные
ошибки.
Пусть t количество значащих цифр в любом действительном числе, тогда при использовании
правила отбрасывания максимальная относительная ошибка округления выразится так:
ey
y
10 t 1
При симметричном округлении максимальная относительная погрешности выразится так:
ey
y
1
10 t 1
2
Формулы относительных ошибок при 4-х арифметических операциях имеют вид:
ex y
x y
x ex
y ex
r
x y x x y y
ex y
e
e
x x r
x y
x
y
ex y
x y
x ey
y ey
r
x y x x y y
ex / y
ey
e
x
r
x/ y
x
y
где r ошибка округления.
44
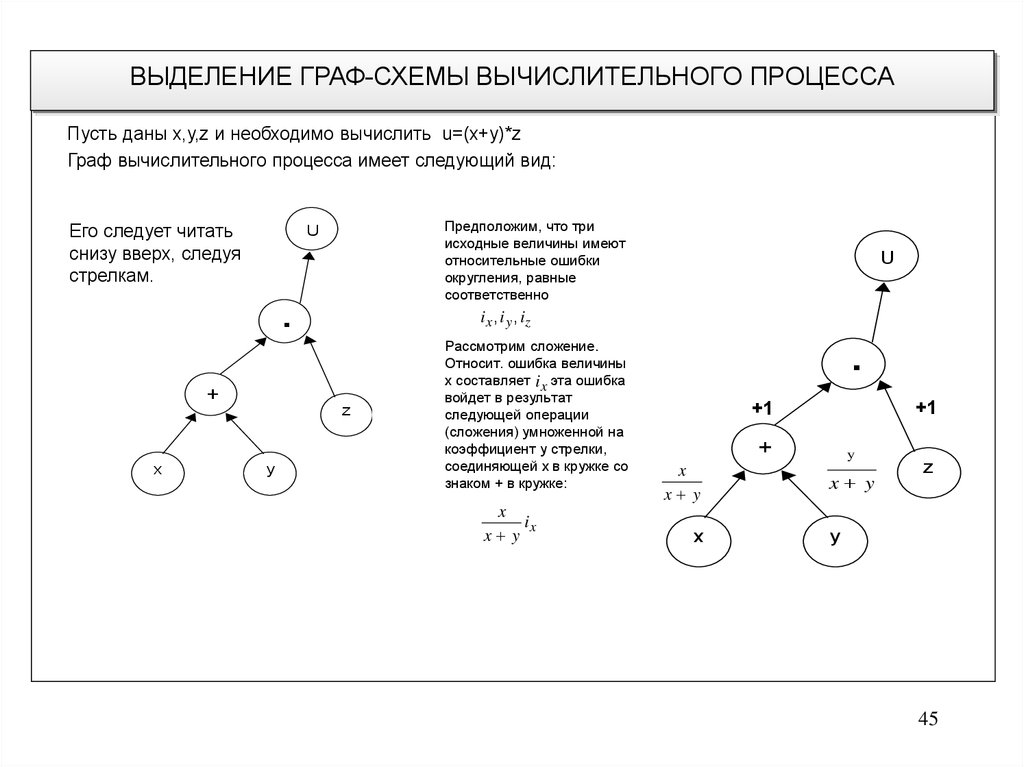
45.
ВЫДЕЛЕНИЕ ГРАФ-СХЕМЫ ВЫЧИСЛИТЕЛЬНОГО ПРОЦЕССАПусть даны x,y,z и необходимо вычислить u=(x+y)*z
Граф вычислительного процесса имеет следующий вид:
Его следует читать
снизу вверх, следуя
стрелкам.
Предположим, что три
исходные величины имеют
относительные ошибки
округления, равные
соответственно
U
.
i x , i y , iz
+
z
x
y
U
Рассмотрим сложение.
Относит. ошибка величины
x составляет i x эта ошибка
войдет в результат
следующей операции
(сложения) умноженной на
коэффициент у стрелки,
соединяющей x в кружке со
знаком + в кружке:
x
ix
x y
.
+1
+1
+
x
x y
x
y
x y
z
y
45
46.
АНАЛИЗ РАСПРОСТРАНЕНИЯ ОШИБОК ОКРУГЛЕНИЯex y
x y
x
y
ix
iy r
1
x y
x y
После выполнения операции умножения появляется ошибка r2. Полная ошибка результата операции
умножения выразится следующим образом:
eu
x
y
ix 1
i y 1 r 1 iz 1 r .
1
2
u
x y
x y
Если все результаты соответствующим образом округлены, то ни одна из ошибок округления не
превзойдет
t
5 10
Поэтому
x
eu
y
3 5 10 t x, y , оба неотрицательные, то
u
x y
x y
x
y
x y
x y
Не может быть больше 1, и окончательно имеем:
eu
20 10 t 2 10 t 1
u
46
47.
ВОЗМОЖНЫЕ ПРИЛОЖЕНИЯ ВЫЧИСЛЕНИЙ С ИСКЛЮЧЕНИЕМ ОШИБОКОКРУГЛЕНИЯ
1. Точное вычисление обобщенных обратных матриц.
Например, таких как, g-обратная матрица Мура-Пенроуза. Многие алгоритмы
требуют умения распознавать значение численного ранга, а это является трудной
задачей при наличии ошибок округления.
2. Целочисленное решение систем линейных уравнений.
Примером могут служить построение оптимальных решений в задачах
целочисленного программирования.
3. Точное вычисление характеристического многочлена матрицы.
Вследствие ошибок округления будут получены приближенные значения
коэффициентов. Если многочлен плохо обусловлен, то корни "приближенного»
характеристического уравнения могут быть плохими приближениями к корням
истинного уравнения.
4. Обращение матриц Гильберта, Адамара и др. особо чувствительных к
ошибкам округления.
5. Для решения промежуточных между классами корректных и некорректных
задач.
Класс задач, изменяющих корректность при решении. Это расчет устойчивости
систем управления, выч. собств. знач. систем лин. одн. урав. и др.
47
48.
Классы задачЗадачи корректные
Вычисления
с исключением
ошибок
округления
Вычислительно
неустойчивые
алгоритмы
Задачи
промежуточные
между корректными
и некорректными
Задачи
некорректные
Плохо
обусловленные
задачи
48
49.
Ф.С. ЗайцевМатематическое моделирование эволюции тороидальной плазмы.
Семашко Н.Н Кафедра физики и ядерного синтеза (МЭИ)
Динамическая устойчивость энергосистем
...
49










































 Математика
Математика Информатика
Информатика








