Предмет и задачи теории игр

1.

Предмет и задачи теории игр.
Основные понятия теории игр:
игра, игроки, партия, выигрыш,
проигрыш, ход, личные и
случайные ходы, стратегические
игры, стратегия, оптимальная
стратегия.

2.

Игра
• Довольно часто в своей практической деятельности человеку приходится
сталкиваться с задачами, в которых необходимо принимать решение в
условиях, когда две или более стороны преследуют различные цели, а
результаты любого действия каждой из сторон зависят от мероприятий
партнера. Такие ситуации, возникающие, например, при игре в шахматы,
шашки или домино, относят к конфликтным: результат каждого хода
игрока зависит от ответного хода противника. Каков будет этот ответный
ход, заранее неизвестно, поэтому говорят, что решение приходится
принимать в условиях неопределенности. Цель игры - выигрыш одного
из участников.
• Ситуация называется конфликтной, если в ней участвуют стороны,
интересы которых полностью или частично противоположны.
• Для рационального решения задач с конфликтными ситуациями
существуют научно обоснованные методы. Такие методы разработаны
математической теорией конфликтных ситуаций, которая
называется теорией игр.
• Игра – это действительный или формальный конфликт, в котором
имеется по крайней мере два участника (игрока), каждый из которых
стремится к достижению собственных целей.

3.

Игра
• Допустимые действия каждого из игроков,
направленные на достижение некоторой цели,
называются правилами игры.
• Игра называется парной, если в ней участвуют два
игрока, и множественной, если число игроков
больше двух. Далее будем рассматривать только
парные игры. В такой игре участвуют два игрока - A
и B, интересы которых противоположны. Под игрой
(процессом игры) будет понимать ряд действий со
стороны A и B.
• Количественная оценка результатов игры
называется платежом.

4.

Выбор и осуществление одного из действий, предусмотренных правилами,
называется ходом игрока. Ходы могут быть личными и случайными.
Личный ход – это сознательный выбор игроком одного из возможных действий
(например, ход в шахматной игре).
Случайный ход – это случайно выбранное действие (например, выбор карты из
перетасованной колоды).
В дальнейшем мы будем рассматривать только личные ходы игроков.
Стратегией игрока называется совокупность правил, определяющих выбор его
действия при каждом личном ходе в зависимости от сложившейся ситуации.
Обычно в процессе игры при каждом личном ходе игрок делает выбор в
зависимости от конкретной ситуации. Однако, в принципе, возможно, что решения
приняты игроком заранее (в ответ на любую сложившуюся ситуацию). Это означает,
что игрок выбрал определенную стратегию, которая может быть задана в виде
списка правил или программы.
Игра называется конечной, если у каждого игрока есть конечное число стратегий,
и бесконечной – в противном случае.
Стратегия игрока называется оптимальной, если она обеспечивает игроку
максимальный выигрыш (или, что то же самое, минимальный проигрыш), при
условии, что второй игрок придерживается своей стратегии.
Если игра повторяется много раз, то игроков может интересовать не выигрыш и
проигрыш в каждой конкретной партии, а средний выигрыш (проигрыш) во всех
партиях.
Для того чтобы решить игру, или найти решение игры, необходимо для каждого из
игроков выбрать оптимальную стратегию.
Таким образом, предмет теории игр составляют методы отыскания оптимальных
стратегий игроков.

5.

Теория игр
• Теория игр — это раздел математической экономики,
изучающий решение конфликтов между игроками и
оптимальность их стратегий. Конфликт может относиться к
разным областям человеческого интереса: чаще всего это
экономика, социология, политология, реже биология,
кибернетика и даже военное дело. Конфликтом является любая
ситуация, в которой затронуты интересу двух и более
участников, традиционно называемых игроками. Для каждого
игрока существует определенный набор стратегий, которые он
может применить. Пересекаясь, стратегии нескольких игроков
создают определенную ситуацию, в которой каждый игрок
получает определенный результат, называемый выигрышем,
положительным или отрицательным. При выборе стратегии
важно учитывать не только получение максимального профита
для себя, но так же возможные шаги противника, и их влияние
на ситуацию в целом.

6.

История
• Основы теории игр зародились еще в 18 веке, с началом эпохи
просвещения и развитием экономической теории. Впервые
математические аспекты и приложения теории были изложены в
классической книге 1944 года Джона фон Неймана и Оскара
Моргенштерна «Теория игр и экономическое поведение». Первые
концепции теории игр анализировали антагонистические игры,
когда есть проигравшие и выигравшие за их счет игроки. Не смотря
на то, что теория игр рассматривала экономические модели,
вплоть до 50-х годов 20 века она была всего лишь математической
теорией. После, в результате резкого скачка экономики США после
второй мировой войны, и, как следствие, большего
финансирования науки, начинаются попытки практического
применения теории игр в экономике, биологии, кибернетике,
технике, антропологии. Во время Второй мировой войны и сразу
после нее теорией игр серьезно заинтересовались военные,
которые увидели в ней мощный аппарат для исследования
стратегических решений.

7.

Теория игр
Автор теории игр — физик, математик и инженер Джон фон Нейман
(в некоторых источниках — Нойман). Под игрой он понимал любую
ситуацию, в которой выполняются такие условия:
• В ней не меньше двух участников.
• У каждого участника свой интерес.
• У каждого участника есть несколько вариантов действий.
• Каждый принимает решения на основании информации о
действиях других.
Есть какие-то общие правила, которые известны всем. Они могут
меняться, сокращаться или расширяться, но они быстро становятся
известны всем.
С этой точки зрения большинство наших бытовых ситуаций попадает
под действие теории игр. Даже обычные переговоры о зарплате или
о том, где провести отпуск, — в них тоже действует теория игр.

8.

Теория игр
• В теории игр используется мощный
математический аппарат. Это значит, что
можно написать или придумать симуляцию
для каждой игры и посмотреть
на возможные результаты при разных
стратегиях игры. Часть стратегий получает
строгое математическое доказательство,
другая — процентную вероятность успеха
при выборе той или иной стратегии.

9.

Стратегия
• Смысл теории игр — найти максимально
выигрышную стратегию для конкретного игрока.
Стратегия — это его последовательность действий:
что он делает и какие сообщения отправляет тем
самым другим игрокам.
• В некоторых играх невозможно выиграть, и в этом
случае лучшей стратегией будет проиграть как
можно меньше или находиться в игре как можно
дольше. Все онлайн-шутеры, где игровое поле
постоянно сжимается — это как раз про такую
стратегию.

10.

Типы игр
• В зависимости от поведения участников и правил, игры можно
поделить на несколько категорий. Они могут пересекаться между
собой.
Кооперативная\некооперативная игра
Кооперативной игрой является конфликт, в котором игроки могут
общаться между собой и объединяться в группы для достижения
наилучшего результата. Примером кооперативной игры можно считать
карточную игру Бридж, где очки каждого игрока считаются
индивидуально, но выигрывает пара, набравшая наибольшую сумму.
Из двух типов игр, некооперативные описывают ситуации в мельчайших
деталях и выдают более точные результаты. Кооперативные
рассматривают процесс игры в целом. Не смотря на то, что эти два вида
противоположны друг другу, вполне возможно объединение стратегий,
которое может принести больше пользы, чем следование какой-либо
одной.

11.

Пример «Дилемме заключенного»
• Двое преступников, А и Б, попались примерно в одно и то же
время на сходных преступлениях. Есть основания полагать, что
они действовали по сговору, и полиция, изолировав их друг от
друга, предлагает им одну и ту же сделку: если один
свидетельствует против другого, а тот хранит молчание, то
первый освобождается за помощь следствию, а второй
получает максимальный срок лишения свободы (10 лет). Если
оба молчат, их деяние проходит по более лёгкой статье, и они
приговариваются к 6 месяцам. Если оба свидетельствуют
против друг друга, они получают минимальный срок (по 2 года).
Каждый заключённый выбирает, молчать или
свидетельствовать против другого. Однако ни один из них не
знает точно, что сделает другой. Что произойдёт?

12.

Представив игру в виде матрицы
мы получим:
Преступник Б
Стратегия «молчать»
Преступник Б
Стратегия «предать»
Преступник А
Стратегия «молчать»
Пол года каждому
10 Лет преступнику А
Отпустить преступника Б
Преступник А
Стратегия «предать»
10 Лет преступнику Б
Отпустить преступника А
2 года каждому
А теперь представим развитие ситуации, поставив себя на место
заключенного А. Если мой подельник молчит, лучше его сдать и выйти на
свободу. Если он говорит, то так же лучше все рассказать, и получить всего
два года, вместо десяти. Таким образом, если каждый игрок выбирает, что
лучше для него, оба сдадут друг друга, и получат два года, что не является
идеальной ситуацией для обоих. Если бы каждый думал об общем благе,
они бы получили всего по пол года.

13.

Типы игр
• С нулевой суммой и с ненулевой суммой
Игрой с нулевой суммой называют игру, в которой
выигрыш одного игрока равняется проигрышу другого.
Например банальный спор: если вы выиграли сумму N, то
кто-то эту же сумму N проиграл. В игре же с ненулевой
суммой может изменяться общая цена игры, таким
образом принося выгоду одному игроку, не отнимаю ее
цену у другого. В качестве примера здесь отлично
подойдут шахматы: превращая пешку в ферзя игрок А
увеличивает общую сумму своих фигур, при этом не
отнимая ничего у игрока Б. В играх с ненулевой суммой
проигрыш одного из игроков не является обязательным
условием, хотя такой исход и не исключается.

14.

Типы игр
• Симметричные и нет. В симметричных играх у каждого игрока
всегда один и тот же набор стратегий, а в несимметричных
стратегии могут быть разные.
• С полной или неполной информацией. В играх с полной
информацией каждый знает все доступные другим игрокам
стратегии и может делать выводы на их основе. В играх
с неполной информацией никто не знает, какую стратегию
выбрал другой участник. Наш пример с пробками как раз
из разряда игр с неполной информацией.
• Параллельные и последовательные. В последовательных играх
все ходят по очереди (необязательно по порядку, но за один
ход действует только один игрок). В параллельных все
действуют одновременно и не знают, что сделали другие, пока
не сделали свой ход. Пример с пробками — это параллельная
игра.

15.

Пример
Пусть игрок А располагает m
личными стратегиями: A1, A2, …, Am.
Пусть у игрока B имеется n личных
стратегий. Обозначим их B1, B2, …, Bn.
В этом случае игра имеет
размерность mxn. В результате
выбора игроками любой пары
стратегий Ai,Bj (i=1,m;j=1,n )
однозначно определяется исход
игры, т.е. выигрыш aij игрока А
(положительный или отрицательный)
и проигрыш ( - aij) игрока В.
Предположим, что значения
aij известны для любой пары
стратегий (Ai,Bj).
Матрица А = (aij), элементами
которой являются выигрыши,
соответствующие стратегиям Ai и Bj,
называется платежной
матрицей или матрицей игры.
A=
a11 a12 ...
a2n
a1n a21 a22 ...
...
am1 am2 ...
amn
.

16.

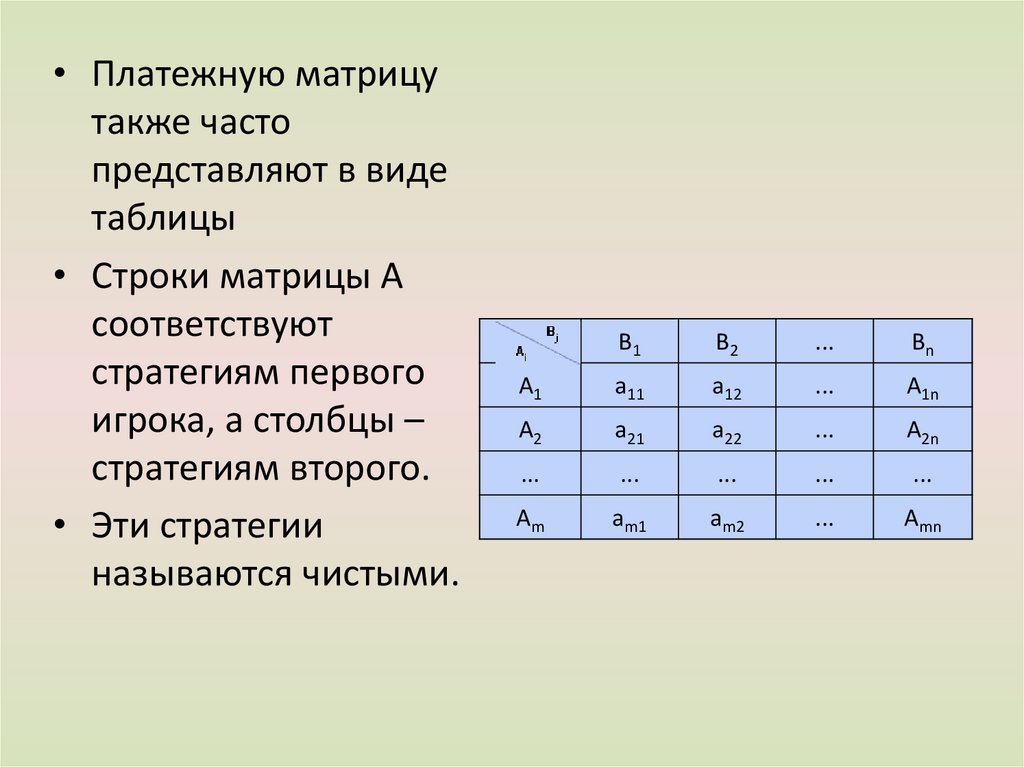
• Платежную матрицу
также часто
представляют в виде
таблицы
• Строки матрицы А
соответствуют
стратегиям первого
игрока, а столбцы –
стратегиям второго.
• Эти стратегии
называются чистыми.
B1
B2
...
Bn
A1
a11
a12
...
A1n
A2
a21
a22
...
A2n
...
...
...
...
...
Am
am1
am2
...
Amn

17.

Игрок А может спрятаться в одном из двух
убежищ (I или II); игрок B ищет игрока A, и если
найдет, то получает штраф 1 денежную единицу
от А, в противном случае - платит игроку А 1
денежную единицу.
Решение.
Для того чтобы составить платежную матрицу
следует проанализировать поведение каждого из
игроков. Игрок А может спрятаться в убежище I обозначим эту стратегию через A1, или в
убежище II - стратегия A2.
Для того чтобы составить платежную матрицу
следует проанализировать поведение каждого из
игроков. Игрок А может спрятаться в убежище I обозначим эту стратегию через A1, или в
убежище II - стратегия A2.
Игрок B может искать первого игрока в убежище I
- стратегия B1, либо в убежище II - стратегия B2.
Если игрок А находится в убежище I и там его
обнаруживает игрок B, т.е. осуществляется пара
стратегий (A1, B1), то игрок А платит штраф, т.е.
a11 = -1. Аналогично a22 = -1.
Очевидно, что комбинации стратегий (A1, B2) и
(A2, B1) дают игроку А выигрыш, равный единице,
поэтому a12= a21 = 1.
Таким образом, для игры "Поиск"
размера 2x2 получаем следующую платежную
матрицу:
A=
-1 1
.
1 -1
Составьте платежную
матрицу для
следующей игры
(игра "Поиск").

18.

При выборе стратегии A1 (первая строка
матрицы) минимальный выигрыш равен a1 =
min (-1; 1) = -1 и соответствует стратегии
B1 игрока B. При выборе стратегии A2 (вторая
строка матрицы) минимальный выигрыш
равен a2 = min (-1; 1) = -1, он достигается при
использовании игроком B стратегии B2.
Гарантируя себе максимальный выигрыш при
любой стратегии игрока B, т.е. нижнюю цену
игры a= max (a1; a2) = max (-1; -1) = -1, игрок А
может выбрать любую стратегию: A1 или A2,
т.е. любая его стратегия является
максиминной.
Выбирая стратегию B1 (первый столбец), игрок
B понимает, что игрок А ответит стратегией A2,
чтобы максимизировать свой выигрыш
(проигрыш игрока B). Следовательно,
максимальный проигрыш игрока B при выборе
им стратегии B1 равен b1 = max (-1; 1) = 1.
Аналогично, максимальный проигрыш игрока
B при выборе им стратегии B2 (второй столбец)
равен b2 = max (1; -1) = 1.
Таким образом, при любой стратегии игрока А
гарантированный минимальный проигрыш
игрока B равен b= min (b1, b2) = min (1, 1) = 1 верхней цене игры.
Любая стратегия игрока B является
минимаксной.
B1
B2
i
A1
-1
1
-1
A2
1
-1
-1
j
1
1

19.

Таким образом, в рассматриваемой задаче нижняя и верхняя цены игры
различны: a≠b .
Если же верхняя и нижняя цены игры совпадают, то общее значение
верхней и нижней цены v = a =b называется чистой ценой игры, или
просто ценой игры. Максиминная и минимаксная стратегии,
соответствующие цене игры, являются оптимальными стратегиями, а их
совокупность – оптимальным решением, или просто решением игры.
В этом случае игрок А получает максимальный гарантированный (не
зависящий от поведения игрока В) выигрыш v, а игрок В добивается
минимального гарантированного (не зависящего от поведения игрока А)
проигрыша v. Говорят, что решение игры обладает устойчивостью, т.е., если
один из игроков придерживается своей оптимальной стратегии, то для
другого не может быть выгодным отклоняться от своей оптимальной
стратегии.
Пара чистых стратегий Ai и Bj дает оптимальное решение игры тогда и только
тогда, когда соответствующий ей элемент aij является одновременно
наибольшим в своем столбце и наименьшим в своей строке.
Такая ситуация, если она существует, называется седловой точкой (по
аналогии с поверхностью седла, которая искривляется вверх в одном
направлении и вниз - в другом).
Таким образом, для игры с седловой точкой нахождение решения
заключается в выборе максиминной и минимаксной стратегии, которые и
являются оптимальными.

20.

Спасибо!
• https://www.youtube.c
om/watch?v=tfXWBhZz
n1E
• https://www.youtube.c
om/watch?v=6iHsp9PA
WJw