Точечные оценки параметров распределения

1. Математическая статистика

2. Статистические оценки параметров распределения

3. Общие понятия статистических оценок

Пусть требуется изучить некоторый количественный
признак генеральной совокупности. Из теоретических
соображений установлен вид распределения этого
признака.
В этом случае имеет место задача оценки
неизвестных параметров известного распределения. При
этом для оценки параметров используется только
выборка значений x1, x2, …, xn, полученных в результате
наблюдений.

4.

Статистической оценкой неизвестного параметра
теоретического распределения называется функция от
наблюдаемых значений случайных величин, то есть
* x1 , x2 ,..., xn .
Пусть * – статистическая оценка неизвестного
параметра теоретического распределения. Для того,
чтобы статистические оценки * давали «хорошие»
приближения,
они
должны
удовлетворять
определенным существующим требованиям.

5. Требования к статистическим оценкам

1. Несмещенность оценки.
Статистическая
оценка
*
называется
несмещенной, если ее математическое ожидание
равно оцениваемому параметру при любом объеме
выборки, то есть M ( * ) .
Если M ( * ) , то
называется смещенной.
статистическая
оценка

6.

2. Состоятельность оценки.
Статистическая
оценка
*
называется
состоятельной для параметра , если она сходится
по вероятности к оцениваемому параметру при
неограниченном возрастании объема выборки
lim p * 1,
n
где – сколь угодно малое положительное число.
Для выполнения данного требования достаточно,
* была
D( * ) 0
чтобы lim
и
чтобы
оценка
n
несмещенной.

7.

3. Эффективность оценки.
Статистическая оценка называется эффективной,
если при заданном объеме выборки n она имеет
наименьшую, возможную дисперсию, то есть
необходимо чтобы
D( * ) Dmin .

8. Выборочное среднее

9.

Пусть для изучения генеральной совокупности
относительно количественного признака Х извлечена
выборка объема n.
Выборочной
средней
называют
среднее
арифметическое
значение
признака
выборочной
совокупности.
Если все значения x1, x2, …, xn признака выборки
объема n различны,
то выборочное среднее
определяется по формуле:
1 n
xB xi ,
n i 1
где xB – выборочное среднее.

10.

Если значения признака x1, x2, …, xk имеют
соответственно частоты n1, n2, …, nk , причем
k
n ni – объем выборки, то
i 1
1 k
xB xi ni .
n i 1
Замечание: Выборочная средняя, найденная по
данным одной выборки, есть определенное число. Если
извлекать другие выборки того же объема из той же
генеральной совокупности, то выборочная средняя
будет изменяться от выборки к выборке.
Таким образом выборочную среднюю
рассматривать как случайную величину.
можно

11.

Следовательно, можно говорить о распределениях
(теоретическом и эмпирическом) выборочной средней и
о числовых характеристиках этого распределения, в
частности, о математическом ожидании и дисперсии
выборочного распределения.
Если по нескольким выборкам достаточно большого
объема из одной и той же генеральной совокупности
будут найдены выборочные средние, то они будут
приблизительно равны между собой – свойство
устойчивости выборочных средних.
Выборочное среднее является состоятельной и
несмещенной оценкой математического ожидания
случайной величины Х.

12. Групповая и общие средние

Допустим, что все значения количественного
признака Х совокупности разбиты на несколько групп.
Рассматривая каждую группу как самостоятельную
совокупность,
можно
найти
ее
среднюю
арифметическую.
Групповой средней называют среднее арифметическое
значений признака, принадлежащих группе.
Общей средней называют среднее арифметическое
значений признака, принадлежащих всей совокупности.

13.

Зная групповые средние и объемы групп, можно
найти общую среднюю: общая средняя равна средней
арифметической групповых средних, взвешенной по
объемам групп.
Замечание: Для упрощения расчета общей средней
генеральной
совокупности
большого
объема
целесообразно разбить ее на несколько групп, найти
групповые средние и по ним общую среднюю.

14.

Пример. Найдите общую среднюю совокупности,
состоящей из двух групп:
хi
ni
1
10
6
15
хi
ni
1
20
Решение:
Найдем групповые средние:
10 1 15 6
20 1 30 5
x1
4; x2
3,4.
10 15
20 30
Найдем общую среднюю:
25 4 50 3,4
x
3,6.
25 50
5
30

15. Дисперсия

16. Выборочная дисперсия

Для того, чтобы охарактеризовать рассеяние
наблюдаемых значений количественного признака
выборки вокруг среднего значения xB рассматривают
сводную характеристику – выборочную дисперсию.
Выборочной дисперсией DВ называется среднее
арифметическое квадратов отклонений наблюдаемых
значений признака от их выборочной средней.
Если все значения x1, x2, …, xn признака выборки
объема n различны, то
2
1 n
DB xi xB .
n i 1

17.

Если значения признака x1, x2, …, xk имеют
соответственно частоты n1, n2, …, nk , причем
n n1 n2
nk , то
2
1 k
DB xi xB ni .
n i 1
Таким образом, выборочная дисперсия есть средняя
взвешенная квадратов отклонений с весами, равными
соответствующим частотам.

18.

Пример. Найдите выборочную дисперсию, если
выборочная
совокупность
задана
таблицей
распределения:
хi
ni
1
20
2
15
3
10
4
5
Решение:
Найдем выборочную среднюю:
20 1 15 2 10 3 5 4 100
xB
2.
20 15 10 5
50
Найдем выборочную дисперсию:
20 (1 2) 2 15 (2 2) 2 10 (3 2) 2 5 (4 2) 2
DB
1.
50

19.

Для расчета выборочной
использовать частную формулу:
DB x 2 xB
2
или
дисперсии
можно
2
1 k
2
DB ni xi xB .
n i 1
Кроме дисперсии, для характеристики рассеяния
значений признака выборочной совокупности вокруг
своего среднего значения
пользуются сводной
характеристикой
–
средним
квадратическим
отклонением.
Выборочным средним квадратическим отклонением
(стандартом) называют квадратный корень из
выборочной дисперсии: B DB .

20.

Для расчета выборочной
использовать частную формулу:
DB x 2 xB
2
или
дисперсии
можно
2
1 k
2
DB ni xi xB .
n i 1
Кроме дисперсии, для характеристики рассеяния
значений признака выборочной совокупности вокруг
своего среднего значения
пользуются сводной
характеристикой
–
средним
квадратическим
отклонением.
Выборочным средним квадратическим отклонением
(стандартом) называют квадратный корень из
выборочной дисперсии: B DB .

21. Групповая, внутригрупповая, межгрупповая и общая дисперсии

Допустим, что все значения количественного признака
Х генеральной или выборочной совокупности разбиты на
k групп.
Групповой дисперсией называют дисперсию значений
признака,
принадлежащих
группе,
относительно
групповой средней:
2
1 k
,
D jгр
x
x
n
i j i
N j i 1
где ni – частота значения хi, j – номер группы, Nj –
объем группы j, xj – групповая средняя группы j.

22.

Пример.
Найдите
групповые
совокупности, состоящей из двух групп:
хi
ni
2
1
4
7
5
2
хi
ni
3
2
Решение:
Найдем групповые средние:
1 2 7 4 2 5
2 3 3 8
x1
4; x2
6.
10
5
Найдем искомые групповые дисперсии:
1 (2 4) 2 7 (4 4) 2 2(5 4) 2
D1
0,6.
10
2 (3 6) 2 3 (8 6) 2
D2
6.
5
дисперсии
8
3

23.

Внутригрупповой дисперсией называют среднюю
арифметическую групповых дисперсий, взвешенную по
объемам групп:
1
Dвнгр N j D jгр ,
n
k
где Nj – объем группы j,
совокупности.
n Nj
j 1
– объем всей

24.

Пример. Найдите внутригрупповую
совокупности, состоящей из двух групп:
хi
ni
2
1
4
7
5
2
хi
ni
дисперсию
3
2
8
3
Решение:
Групповые дисперсии: D1 0,6, D2 6.
Искомая внутригрупповая дисперсия равна:
1
10 0,6 5 6 12
Dвнгр N1 D1 N 2 D2
2,4.
n
10 5
5

25.

Межгрупповой дисперсией называют дисперсию
групповых средних относительно общей средней:
1
Dмежгр N j ( x j x) 2 ,
n
Общей дисперсией называют дисперсию значений
признака всей совокупности относительно общей средней:
2
1 k
D( x) xi x ni .
n i 1
где n – объем всей совокупности, x – общая средняя,–
ni – частота значения xi, x j – групповая средняя группы j,
Nj – объем группы.

26.

Пример. Найдите межгрупповую дисперсию по
данным предыдущего примера.
Решение:
Найдем общую среднюю и групповые средние:
1 2 7 4 2 5 2 3 3 8 14
x
, x1 4, x2 6.
10 5
3
Найдем межгрупповую дисперсию:
2
2
14
14
10 4 5 6
2
2
N1 ( x1 x) N 2 ( x2 x)
8
3
3
Dмежгр
.
n
10 5
9
Замечание: D( x) Dвнгр Dмежгр .

27.

Выборочная дисперсия DВ является состоятельной, но
смещенной оценкой D(х). Это означает, что если в
качестве
оценки
дисперсии
D(х)
генеральной
совокупности принять DВ выборочной совокупности, то
эта оценка будет приводить к систематическим ошибкам,
давая заниженное значение, так как
n 1
M ( DB )
D( x).
n
Такое смещение особенно проявляется при малых
объемах выборки. В качестве несмещенной оценки D(х)
используется исправленная дисперсия:
n
S
DB .
n 1
2

28.

n
n
2
2
n
1
1
2
S
xi xB
xi xB
n 1 n i 1
n 1 i 1
или для взвешенного статистического ряда:
k
2
1
2
.
S
x
x
n
i
B
i
n 1 i 1
Для оценки среднего квадратического отклонения
генеральной совокупности используют «исправленное»
среднее
квадратическое
отклонение,
которое
определяется по формуле:
2
1 k
.
S
x
x
n
i
B
i
n 1 i 1

29.

Замечание: Сравнивая формулы
k
1 k
1
2
2
2
DB xi xB ni и S
xi xB ni
n i 1
n 1 i 1
видим, что они отличаются только знаменателями.
Очевидно, что достаточно больших значениях n объема
выборки, выборочная и исправленная дисперсия
различаются мало.
На практике пользуются исправленной дисперсией,
если n 30.

30.

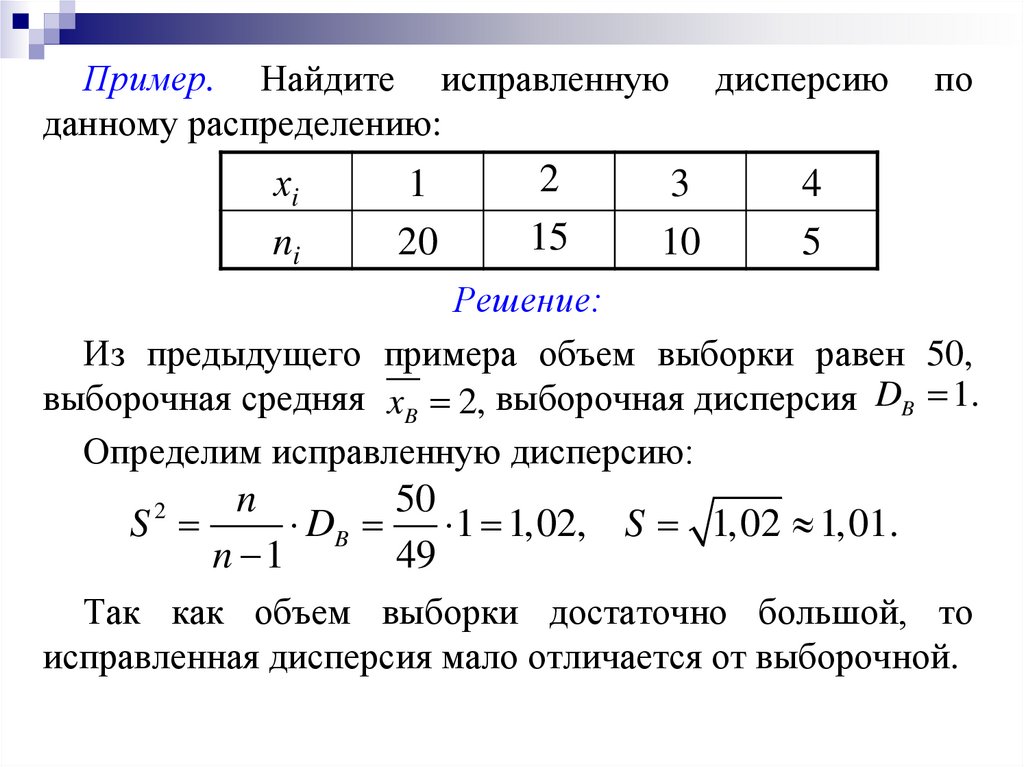
Пример. Найдите исправленную
данному распределению:
хi
ni
1
20
2
15
3
10
дисперсию
по
4
5
Решение:
Из предыдущего примера объем выборки равен 50,
выборочная средняя xB 2, выборочная дисперсия DB 1.
Определим исправленную дисперсию:
n
50
S
DB
1 1,02, S 1,02 1,01.
n 1
49
2
Так как объем выборки достаточно большой, то
исправленная дисперсия мало отличается от выборочной.