Похожие презентации:
Точечные и интервальные оценки неизвестных параметров распределения
1. Лабораторная работа Точечные и интервальные оценки неизвестных параметров распределения
2.
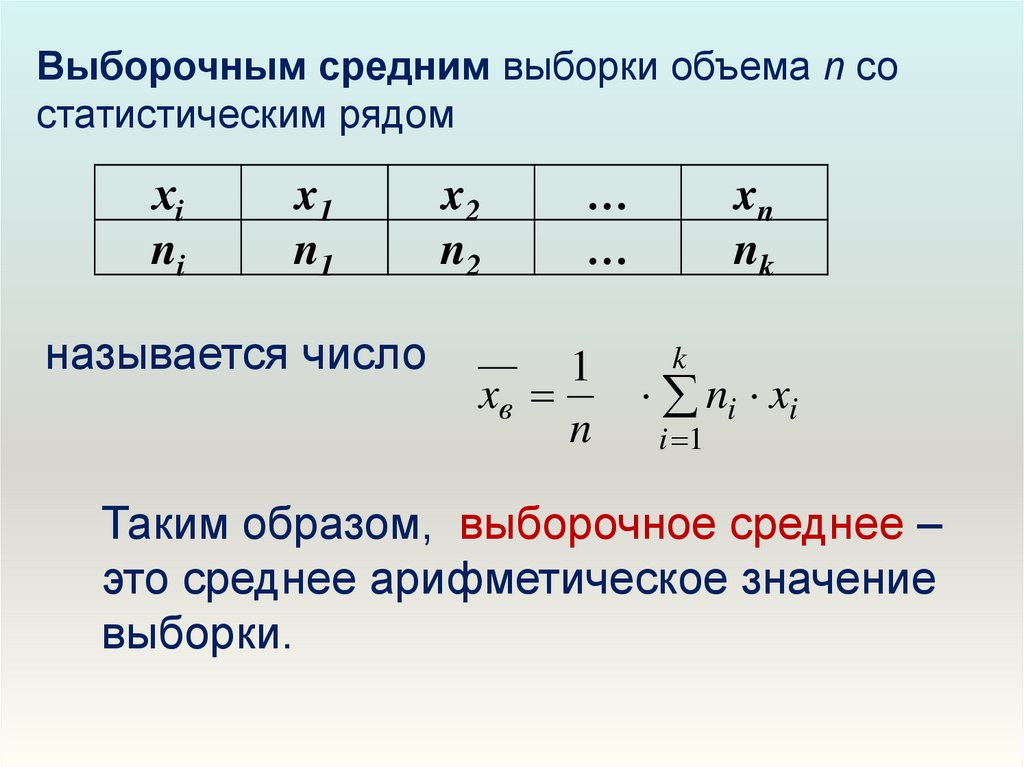
Выборочным средним выборки объема n состатистическим рядом
хi
ni
x1
n1
называется число
x2
n2
…
…
1
xв
n
xn
nk
k
ni xi
i 1
Таким образом, выборочное среднее –
это среднее арифметическое значение
выборки.
3.
Выборочной дисперсией Дв выборки объема n состатистическим рядом
хi
ni
x1
n1
называется число
x2
n2
…
…
xn
nk
1
Д в ni ( xi xв ) 2
n
Таким образом, выборочная дисперсия – это среднее
арифметическое квадратов отклонений наблюдаемых
значений признака от их среднего значения x .
в
Квадратный корень из выборочной дисперсии
называется выборочным средним квадратичным
отклонением величины х
в Дв
4.
В статистике при малых n наряду с выборочнойдисперсией используется другая важная числовая
характеристика выборки: исправленная дисперсия
n
S
Dв
n 1
2
в
Квадратный корень из исправленной выборочной
дисперсии называется исправленным средним
квадратичным отклонением
Sв S
2
в
5.
Пусть дана случайная величина x закон распределения ипараметры (математическое ожидание, дисперсия)
которой неизвестны. Случайную величину х можно
рассмотреть, как генеральную совокупность, которая в
полном объеме, вообще говоря, остается неизвестной.
Однако в результате опыта, наблюдений мы можем
получить некоторую последовательность значений этой
случайной величины, которая представляет собой
определенную выборку из генеральной совокупности.
Для полученной из опыта выборки можно вычислить
выборочное среднее, выборочную дисперсию,
исправленную выборочную дисперсию. При помощи
полученных выборочных параметров оценивают
неизвестные параметры случайной величины х
(генеральной совокупности).
6.
Именно, выборочное среднеехв
берется в качестве оценки (приближенного
значения) математического ожидания М(х)
принимают в качествеМ
оценки
Д(х)
( х) дисперсии
хв
случайной величины х
Выборочную дисперсию Дв и выборочную исправленную
дисперсию S 2
в
принимают в качестве оценки дисперсии Д(х)
случайной величины х
Д ( х) Д в
Д ( х) S
2
в
7.
Точечные оценки указывают точку на числовой прямой,являющуюся приближенным значением неизвестного
параметра. С возрастанием n (то есть для больших
выборок) возрастает точность приближений
М ( х) х в
Д ( х) S
2
в
При небольшом числе испытаний эти значения могут
значительно отличаться от истинных величин
оцениваемых параметров.
По этой причине при небольшом объёме
выборки
следует пользоваться интервальными оценками.
Интервальной оценкой называется оценку, которая
определяется двумя числами – концами интервала.
8.
Пусть, найденная по данным выборки, статистическаяхарактеристикаQ. служит оценкой неизвестного параметра Q
Чем меньше абсолютная величина разности Q и Q
тем точнее определяет параметр Q.
Q Q
*
если 0
Таким образом, положительной число
точность оценки.
характеризует
Надежностью (доверительной вероятностью)
оценки Q и Q называется вероятностью,
с которой осуществляется неравенство
Q Q
*
9.
далее10. Известная дисперсия
1 k
Xв Xi
n i 1
Найти .
По заданному
значению
надежности β по
таблице найти t.
Вычислить ширину
интервала по
формуле
.
Записать ответ в
виде:
t
n
x a x
11. Неизвестная дисперсия
x a x12. СКО
• Величина q = q (n,β) находится поспециальной таблице
• При q < 1
• При q > 1













 Математика
Математика








