ИнÑ‚ервальные оценки параметров распределения

1. Математическая статистика

2. Интервальные оценки параметров распределения

3.

Статистические оценки, определяемые одним
числом, называются точечными. Все рассмотренные
ранее статистические оценки являются точечными.
Надежность (достоверность) точечных оценок
существенно зависит от объема выборки, по
которой они определяются. При выборках малого
объема точечная оценка может существенно
отличаться от оцениваемого параметра, то есть
может приводить к грубым ошибкам.
По этой причине при небольшом объеме выборки
следует пользоваться интервальными оценками.

4.

Интервальной называется статистическая оценка,
которая определяется двумя числами – концами
интервала.
Интервальные оценки позволяют определить
точность и надежность оценки статистического
параметра.
Пусть θ* – статистическая оценка неизвестного
параметра θ. Причем θ может быть как постоянной,
так и случайной величинами.
Точностью статистической оценки называется
величина , определяемая из равенства:
* .

5.

Последнее выражение показывает, чем точнее
параметр θ* описывает θ, тем меньше разность между
ними, то есть меньше величина .
В то же время статистические методы не позволяют
категорически утверждать, что оценка θ* всегда
удовлетворяет неравенству | θ– θ* | < .
Можно лишь говорить о некоторой вероятности
выполнения этого неравенства.
Надежностью
(доверительной
вероятностью)
оценки параметра θ по θ* называется вероятность или
β, с которой осуществляется неравенство
* .

6.

Доверительная вероятность определяет степень
надежности получаемых результатов.
Величина =1– , называется уровнем значимости.
Доверительная вероятность или уровень значимости
задаются исследователем в соответствии с требуемым
уровнем
надежности
результатов.
Чем
более
ответственны результаты, тем больше доверительная
вероятность, то есть имеет значение ближе к единице.
Наиболее часто задают равным 0.95; 0.99; 0.995;
0.999.

7.

В соответствии с определением доверительной
вероятности можно записать, что
P * ,
тогда имеем
P( * ) , или
P( * * ) .
Последнее выражение представляет вероятность того,
что интервал (θ*– , θ*+ ) заключает в себя (покрывает)
неизвестный параметр θ.
*- *
*+
Интервал (θ*– , θ*+ ), покрывающий неизвестный
параметр θ с надежностью , называется доверительным
интервалом.

8. Доверительные интервалы для оценки математического ожидания нормального распределения

9. Доверительные интервалы для оценки математического ожидания нормального распределения при известном σ

Пусть количественный признак Х генеральной
совокупности распределен нормально, причем
среднее квадратическое отклонение σ этого
распределения известно.
Требуется оценить неизвестное математическое
ожидание а по выборочной средней x , то есть
найти доверительные интервалы, покрывающие
параметр а с заданной надежностью .

10.

Для этого необходимо, чтобы выполнялось соотношение:
P X a ,
где – заданная надежность.
Пользуясь формулой вероятности заданного отклонения
P X a 2 ,
заменив Х на X и ( X )
, получим
n
n
n
.
P X a 2
2 (t ), где t
Из последнего равенства найдем t
n
.

11.

Приняв во внимание, что вероятность Р задана и равна
, окончательно получим:
P x t
a x t
2 (t ) .
n
n
где n – объем выборки, x – выборочная средняя, Ф(t) –
функция Лапласа, t – аргумент функции Лапласа,
определяемый по таблице из условия что 2Ф(t) = .
Смысл
полученного
соотношения
таков:
с
надежностью можно утверждать, что доверительный
интервал x ; x покрывает неизвестный параметр
а, с точностью оценки t .
n

12.

Из формулы t
, определяющей точность оценки
n
можно сделать следующие выводы:
1) при увеличении объема выборки n число δ убывает
и, следовательно, точность оценки увеличивается;
2) увеличение надежности оценки =2Ф(t) приводит к
увеличению t (Ф(t) – возрастающая функция), и
возрастанию δ, то есть увеличение надежности оценки
влечет за собой уменьшение ее точности.

13.

Пример. Случайная величина Х имеет нормальное
распределение с известным средним квадратическим
отклонением σ=3. Найти доверительные интервалы для
оценки неизвестного математического ожидания а по
выборочным средним x , если объем выборки n=36,
надежность оценки =0.95.
Решение:
Найдем t. Из соотношения 2Ф(t)=0.95 получим
Ф(t)=0.475. По таблице приложения имеем t=1.96.
Найдем точность оценки:
1.96 3
t
0.98.
n
36
Тогда доверительные интервалы: x 0.98; x 0.98 .

14.

Рассматривая различные значения выборочного
среднего, будем получать доверительные интервалы.
Например, если x 4.1 , то доверительный интервал
имеет следующие доверительные границы:
x 4.1 0.98 3.12
x 4.1 0.98 5.08
Доверительный интервал: 3.12; 5.08 .
Таким образом, значения неизвестного параметра а,
согласующиеся с данными выборки, удовлетворяют
неравенству: 3.12 a 5.08.

15.

Пример. Найти минимальный объем выборки, при
котором с надежностью 0.975, точность оценки
математического ожидания генеральной совокупности
по выборочному среднему равна 0.3, если известно
среднее квадратическое отклонение =1.2 нормально
распределенной генеральной совокупности.
Решение:
Воспользуемся формулой, определяющей точность
оценки
математического
ожидания
генеральной
совокупности по выборочной средней:
t
n
откуда
n
t 2 2
2
.

16.

По условию =0.975, следовательно,
0.975
(t )
0.4875.
2
По таблице найдем t=2.24.
Подставив в выражение, определяющее n, t=2.24,
=1.2, =0.3 найдем
(2.24) 2 (1.2) 2
n
80.2816.
2
(0.3)
Тогда искомый объем выборки n = 81.

17. Доверительные интервалы для оценки математического ожидания нормального распределения при неизвестном σ

Пусть количественный признак Х генеральной
совокупности распределен нормально, причем среднее
квадратическое отклонение σ неизвестно.
В этом случае для построения доверительного
интервала для а определяется случайная величина
(статистика Стьюдента).
( x a) n
T
,
S
где S – исправленное среднее квадратическое
отклонение.

18.

Величина Т имеет распределение Стьюдента с числом
степени свободы ν=n–1 и плотностью распределения
n
n
t2 2
2
f (t , n) Bn 1
,
где
B
,
n
n 1
n 1
(n 1)
2
Г – известная гамма – функция.
Распределение Стьюдента определяется объемом
выборки n и не зависит от неизвестных параметров а и
, при n переходит в нормальное распределение.

19.

Значение случайной величины Т обозначают через t .
В этом случае можно записать, что
S
S
P x t
a x t
,
n
n
где t – табличное значение статистики Стьюдента,
определяемое по таблицам критических значений
распределения Стьюдента при известных n и .
В этом случае доверительный интервал для оценки
математического ожидания а определяется выражением:
x , x где t S .
n

20.

Пример. Количественный признак Х генеральной
совокупности распределен нормально. По
выборке
объема n=16 найдены выборочная средняя x 20.2 и
исправленное среднее квадратическое отклонение S=0.8.
Оценить неизвестное математическое ожидание при
помощи доверительного интервала с надежностью
=0.95.
Решение:
В таблице приложения по =0.95 и n=16 найдем tγ =2.13.
Найдем доверительные границы:
t S
t S
0.8
x
20.2 2.13
19.774, x
20.626.
n
16
n
С надежностью 0.95 неизвестный параметр а заключен в
доверительном интервале 19.774 a 20.626.

21.

Пример. Для определения средней урожайности
пшеницы на площади 10000 га определена средняя
урожайность на 1000 га. Результаты выборочного
исследования представлены в виде следующего
распределения
Урожайность
ц/га
Количество
гектар
11-13
13-15
15-17
17-19
150
200
450
200
Оценить с надежностью =0.95 среднюю
урожайность на всем массиве по выборочной средней
при помощи доверительного интервала.

22.

Решение:
Найдем выборочную среднюю. За значение варианты
примем середины интервалов.
12 150 14 200 16 450 18 200
x
15.4.
1000
Найдем выборочную дисперсию.
(12 15.4)2 150 (14 15.4)2 200
DB
1000
(16 15.4)2 450 (18 15.4) 2 200
3.64.
1000
Так как объем выборки достаточно большой, то
заменим
S
выборочным
среднеквадратическим
отклонением D 3.64 1.91.
B
B

23.

По таблице значений статистики Стьюдента при
n>120 и = 0.95 найдем t = 1.96.
Найдем доверительные границы:
t S
1.91
x
15.4 1.96
15.4 0.118 15.282,
n
1000
t S
1.91
x
15.4 1.96
15.4 0.118 15.518.
n
1000
Доверительный интервал: 15.282 a 15.518.
Полученный доверительный интервал означает, что
выбранная средняя x 15.4
оценивает среднюю
урожайность на площади в 10000 га с точность =0.118
и вероятностью 0.95.

24. Доверительные интервалы для оценки среднего квадратического отклонения нормального распределения

25. Доверительные интервалы для оценки среднего квадратического отклонения σ нормального распределения

Пусть количественный признак Х генеральной
совокупности распределен нормально. Требуется
оценить неизвестное среднее квадратическое отклонение
σ по исправленному среднему квадратическому
отклонению S.
Требуется
найти
доверительные
интервалы,
покрывающие параметр σ с заданной надежностью .
Потребуем, чтобы выполнялось условие:
P S
или
P S S .

26.

Преобразуем неравенство S S к виду
S 1 S 1 .
S
S
Обозначим через q
S
, получим:
S (1 q) S (1 q)
доверительный интервал, покрывающий σ с заданной
надежностью .
q – находят по специальным таблицам при заданных
и n.
Замечание. Выражение S (1 q) S (1 q)
используется только при q<1. Если q>1, то
неравенство имеет вид 0 S (1 q).

27.

Пример. Количественный признак Х генеральной
совокупности распределен нормально. По
выборке
объема
n=10
найдено
исправленное
среднее
квадратическое отклонение S=0.16. Найти доверительный
интервал,
покрывающий
генеральное
среднее
квадратическое отклонение σ с надежностью =0.999.
Решение:
В таблице приложения по =0.999 и n=10 найдем
q=1.80. Здесь q>1, следовательно, доверительный
интервал имеет вид:
0 S (1 q),
0 0.16 (1 1.80),
0 0.448.

28.

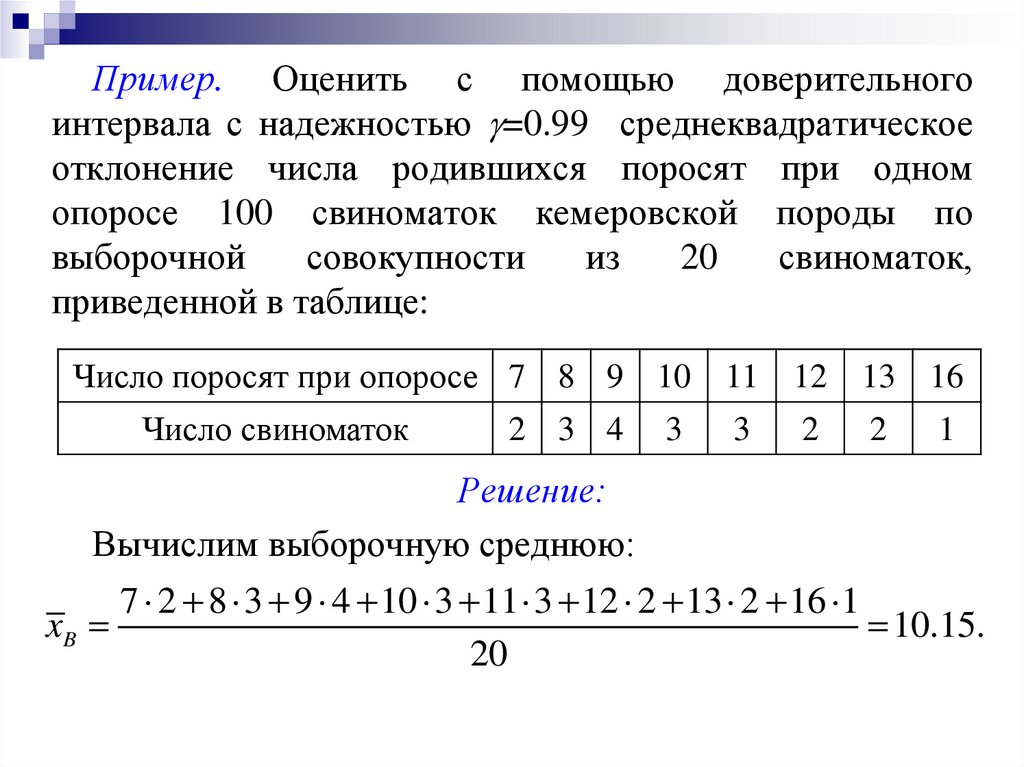
Пример. Оценить с помощью доверительного
интервала с надежностью =0.99 среднеквадратическое
отклонение числа родившихся поросят при одном
опоросе 100 свиноматок кемеровской породы по
выборочной
совокупности
из
20
свиноматок,
приведенной в таблице:
Число поросят при опоросе 7 8 9 10
Число свиноматок
2 3 4
3
11
12 13 16
3
2
2
1
Решение:
Вычислим выборочную среднюю:
7 2 8 3 9 4 10 3 11 3 12 2 13 2 16 1
xB
10.15.
20

29.

Найдем выборочную дисперсию:
2
2
DB xB 2 xB 107.95 10.15 4.93.
Определим исправленную дисперсию:
n
20
2
S
DB 4.93 5.19, S S 2 2.28.
n 1
19
По таблице определим, что при n=20 и =0.99, q=0.58.
Найдем оценку среднего квадратического отклонения
по формуле: S (1 q) S (1 q) , тогда
2.28(1 – 0.58) < < 2.28(1 + 0.58),
0.96 < < 3.6 или 2.28 – 1.32 < < 2.28 + 1.32.
Таким образом, с вероятностью 0.99 можно
утверждать, что точность оценки по выборочному
исправленному среднему квадратическому отклонению
равна 1.32.

30. Оценки точности измерений

В теории ошибок принято точность измерений
(точность прибора) характеризовать при помощи
среднего квадратического отклонения σ случайных
ошибок измерений. Для оценки σ используют
исправленное среднее квадратическое отклонение S.
Поскольку
результаты
измерений
взаимно
независимы, имеют одно и тоже математическое
ожидание (истинное значение измеряемой величины) и
одинаковую дисперсию (для равноточных измерений),
то для оценки измерений используют формулу:
S (1 q) S (1 q).

31.

Пример. По 15 равноточным измерениям найдено
исправленное среднее квадратическое отклонение S=0.12.
Найти точность измерений с надежностью =0.99.
Решение:
Точность
измерений
характеризуется
средним
квадратическим отклонением σ случайных ошибок,
поэтому задача сводится к определению доверительного
интервала, покрывающего σ с заданной надежностью
=0.99.
В таблице приложения по =0.99 и n=15 найдем q=0.73.
Искомый доверительный интервал имеет вид:
0.12(1 0.73) 0.12(1 0.73)
или
0.03 0.21.