Использование нелинейного процессора (физическая нелинейность) для расчета монолитных конструктивных систем по требованиям СП

1.

к.т.н.
Ходыкин
Владислав
Владимирович,
НОНО
«Управление
государственной
Ходыкин
Владислав
Владимирович,
к. т. ГАУ
н., ГАУ
«Управление
государственной
экспертизыпроектной
проектнойдокументации
документации по
экспертизы
по Нижегородской
Нижегородскойобласти»
области»
Анущенко Александр Михайлович, ООО МСК «Мост-К»
Бойчук Иван Андреевич, ООО МСК «Мост-К»
Шевцов Андрей Алексеевич, ООО МСК «Мост-К»
Использование нелинейного процессора
(физическая нелинейность) для расчета
монолитных конструктивных систем по
требованиям СП 430.1325800.2018 в среде SCAD
Office
Московский международный семинар
«Расчет и проектирование конструкций в среде SCAD Office 21»
г. Москва, 21 апреля 2020 г.

2.

Готовы ли мы перейти к нелинейному анализу при проектировании?
/Перельмутер А. В. , Тур В. В./
• Действующие нормы рассматривают, главным образом, проектирование сечений или
отдельных элементов и практически не содержат правил проектирования
конструктивных систем, к которым собственно и применим нелинейный анализ.
• Нелинейный анализ может быть связан с отсутствием однозначности решения
(например, возможность реализации более чем одного состояния устойчивого равновесия, к
которым можно прийти, используя различные истории нагружения).
• Динамические расчеты, тесно привязаны к таким понятиям линейной динамики сооружений, как частоты и формы собственных колебаний системы. Для нелинейной системы
исчезает само понятие отдельных форм собственных колебаний и все основанные на
этом рекомендации (имеющие в виду процедуру разложения движений по формам свободных колебаний системы), теряют свой смысл.
• Нелинейные расчеты следует рассматривать как некоторый более совершенный, но
дополнительный инструмент, который используют в тех случаях, когда применение
простых стандартных методов расчета сечений является недостаточным и не дает полный
информации о поведении конструктивной системы.

3.

СП 430.1325800.2018 Монолитные конструктивные системы.
Правила проектирования.
Требования к расчету монолитных конструктивных систем.
6.2.4 Расчет монолитных конструктивных систем производят с применением линейных и
нелинейных жесткостей железобетонных элементов.
• Линейные жесткости железобетонных элементов, осуществляющие связь усилий с
упругими (линейными) деформациями, определяют как для сплошного упругого тела.
• Нелинейные жесткости железобетонных элементов определяют по поперечному сечению
элементов с учетом возможного образования трещин и развития неупругих (нелинейных)
деформаций в бетоне и арматуре, соответствующих кратковременному и длительному
действиям нагрузки.
6.2.5 Значения нелинейных жесткостей железобетонных элементов следует устанавливать в
зависимости от стадии расчета, требований к расчету и характера напряженнодеформированного состояния элемента.

4.

СП 430.1325800.2018 Монолитные конструктивные системы.
Правила проектирования.
• На первой стадии расчета конструктивной системы, характеризуемой тем, что армирование
железобетонных элементов неизвестно, нелинейную работу элементов допускается учитывать,
применяя нелинейную жесткость, определяемую понижением их линейных жесткостей (или модуля
упругости бетона) с помощью условных понижающих коэффициентов.
6.2.9. В первом приближении значения условных понижающих коэффициентов допускается
принимать равными:
• 0,6 - для вертикальных несущих элементов;
• 0,2 - для горизонтальных несущих элементов при наличии трещин;
• 0,3 - для горизонтальных несущих элементов при отсутствии трещин.
• На последующих стадиях расчета конструктивной системы, когда известно армирование
железобетонных элементов, в расчет следует вводить в зависимости от вида определяемого
параметра конструктивной системы (6.2.1) уточненные значения нелинейных жесткостей
элементов, учитывающие армирование, образование трещин и развитие неупругих деформаций в
бетоне и арматуре согласно СП 63.13330.

5.

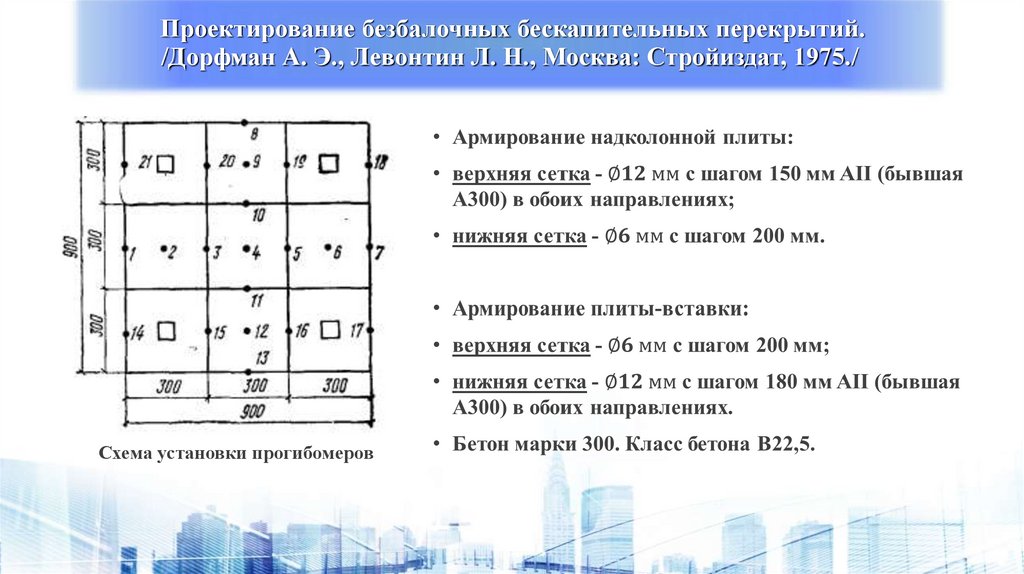
Проектирование безбалочных бескапительных перекрытий.
/Дорфман А. Э., Левонтин Л. Н., Москва: Стройиздат, 1975./
Схема последовательного нагружения конструкции

6.

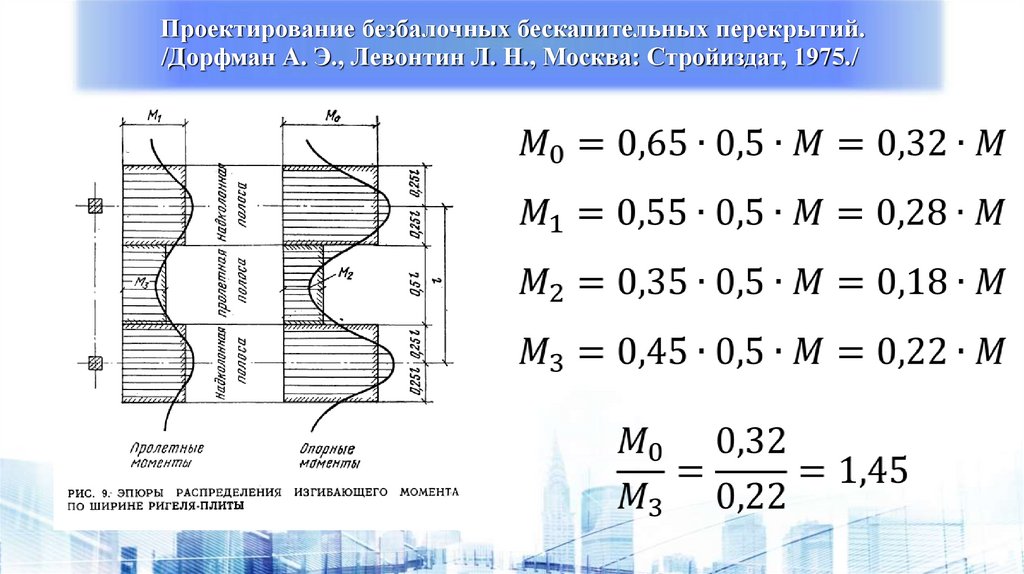
Проектирование безбалочных бескапительных перекрытий.
/Дорфман А. Э., Левонтин Л. Н., Москва: Стройиздат, 1975./

7.

Проектирование безбалочных бескапительных перекрытий.
/Дорфман А. Э., Левонтин Л. Н., Москва: Стройиздат, 1975./
Схема установки прогибомеров

8.

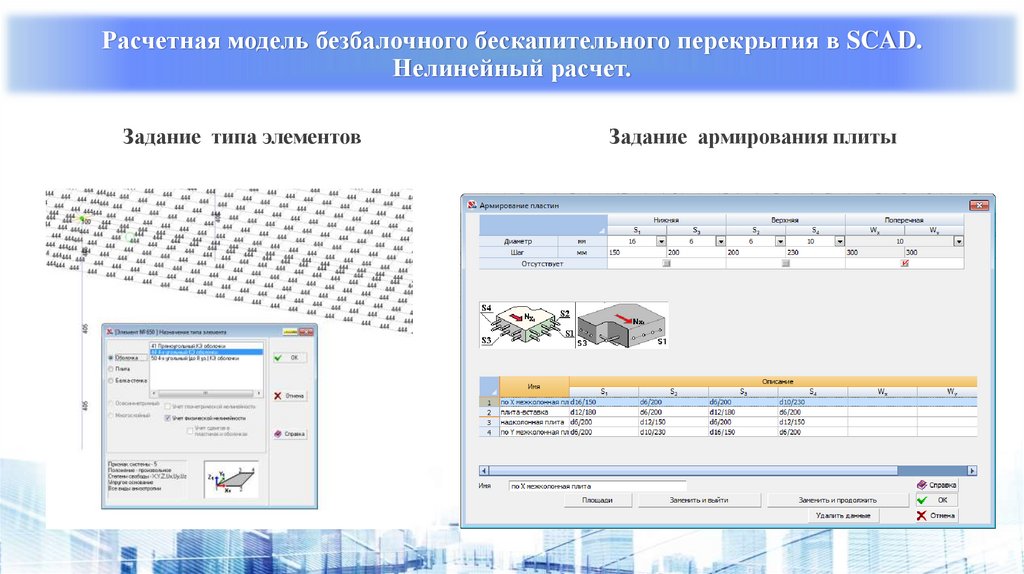
Расчетная модель безбалочного бескапительного перекрытия в SCAD.
Нелинейный расчет.
Задание типа элементов
Задание армирования плиты

9.

Расчетная модель безбалочного бескапительного перекрытия в SCAD.
Нелинейный расчет.

10.

Расчетная модель безбалочного бескапительного перекрытия в SCAD.
Нелинейный расчет.
Межколонная плита
Надколонная плита

11.

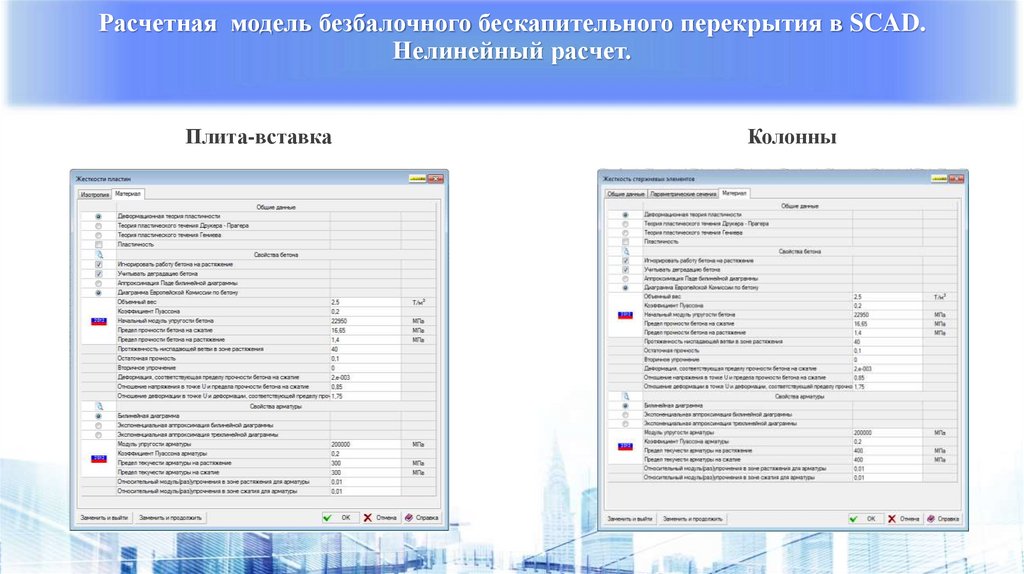
Расчетная модель безбалочного бескапительного перекрытия в SCAD.
Нелинейный расчет.
Плита-вставка
Колонны

12.

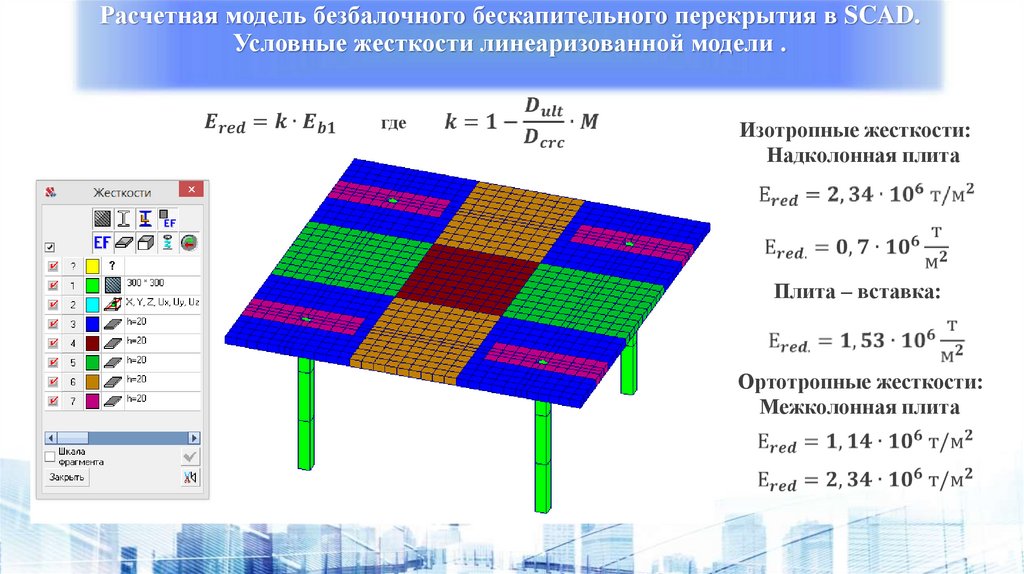
Расчетная модель безбалочного бескапительного перекрытия в SCAD.
Условные жесткости линеаризованной модели .
где
Изотропные жесткости:
Надколонная плита
Плита – вставка:
Ортотропные жесткости:
Межколонная плита

13.

Расчетная модель безбалочного бескапительного перекрытия в SCAD.
Изгибающие моменты в плите.
Экспериментальные данные:
М надколонный / М пролетный =
1,45
Нелинейный расчет:
М надколонный / М пролетный =
1,55
Линеаризованный расчет:
М надколонный / М пролетный =
Эпюра изгибающих моментов в плите.
1,52

14.

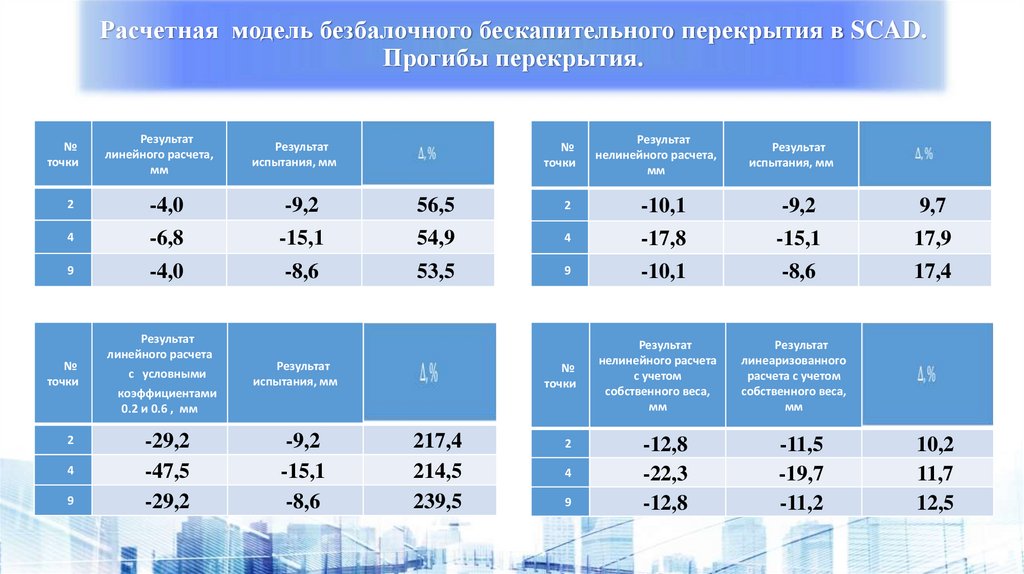
Расчетная модель безбалочного бескапительного перекрытия в SCAD.
Прогибы перекрытия.
№
точки
Результат
линейного расчета,
мм
Результат
испытания, мм
2
-4,0
-9,2
4
-6,8
9
-4,0
№
точки
2
4
9
Результат
линейного расчета
с условными
коэффициентами
0.2 и 0.6 , мм
-29,2
-47,5
-29,2
№
точки
Результат
нелинейного расчета,
мм
Результат
испытания, мм
56,5
2
-10,1
-9,2
9,7
-15,1
54,9
4
-17,8
-15,1
17,9
-8,6
53,5
9
-10,1
-8,6
17,4
№
точки
Результат
нелинейного расчета
с учетом
собственного веса,
мм
Результат
линеаризованного
расчета с учетом
собственного веса,
мм
-12,8
-22,3
-12,8
-11,5
-19,7
-11,2
Результат
испытания, мм
-9,2
-15,1
-8,6
217,4
214,5
239,5
2
4
9
10,2
11,7
12,5

15.

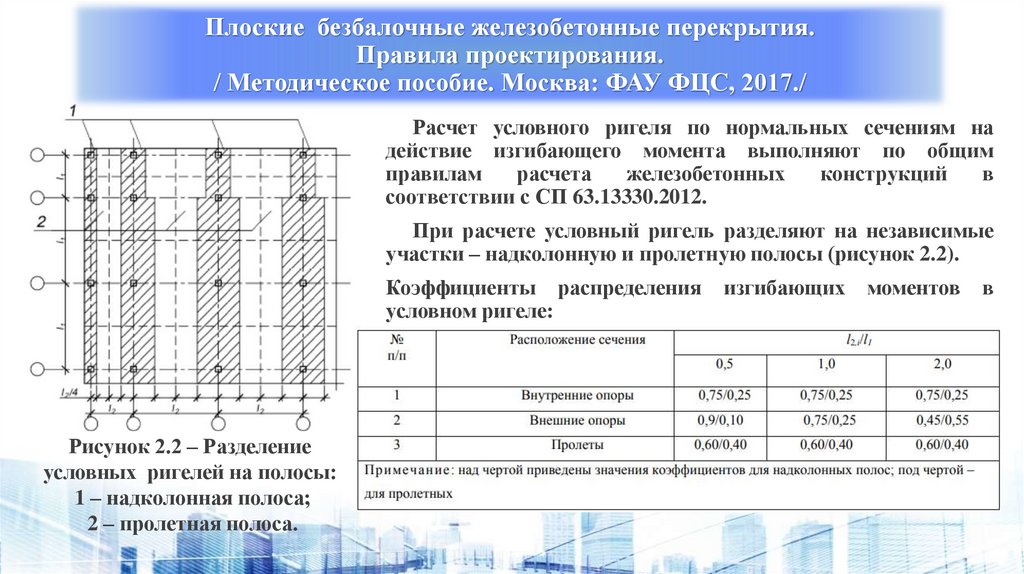
Плоские безбалочные железобетонные перекрытия.
Правила проектирования.
/ Методическое пособие. Москва: ФАУ ФЦС, 2017./
«В качестве примера разработана пространственная каркасная конструкция
безбалочного каркаса, с размерами пролетной ячейки 7,2×6 м. Высота этажа 3 м.
Плита принята толщиной 200 мм, колонны 400×400 мм.
Моделирование выполняется в линейной (упругой) и нелинейной (неупругой)
постановках задачи.
В качестве расчетной модели использована пространственная стержневая модель,
в которой колонны заданы универсальными пространственными стержневыми
элементами, а железобетонные плиты перекрытий заданы универсальными
четырехугольными элементами оболочки с шагом триангуляционной сетки 0,2 м.
Кроме того, моделирование зон опирания плиты перекрытия на колонны выполнено с
помощью так называемых «Абсолютно жестких тел (АЖТ)». Учет неупругой работы
(физическая нелинейность) учтен косвенно, с помощью пониженных значений модуля
упругости материалов в соответствии с СП. Модуль упругости для КЭ плит
принимается пониженным с коэффициентом 0,3 (при вычислении усилий) и 0,2 (при
вычислении перемещений), учитывающим ползучесть бетона и наличие трещин».

16.

Плоские безбалочные железобетонные перекрытия.
Правила проектирования.
/ Методическое пособие. Москва: ФАУ ФЦС, 2017./
«Модуль упругости для вертикальных элементов принимается с коэффициентом
0,6, учитывающим только ползучесть бетона.
При моделировании нелинейной модели в качестве рабочих диаграмм приняты
упрощенные двухлинейные диаграммы по типу диаграмм Прандтля.
В качестве основного армирования плиты (по всей площади плиты) принято
горизонтальное армирование из арматуры класса А500С в виде стержней диаметром
12 мм с шагом 200 мм. Также в рассматриваемой опорной зоне установлено
дополнительное армирование из стержней диаметром 16 мм с шагом 200 мм.
Выполняется расчет нелинейной конечно-элементной модели. В результате расчета
получена картина усилий с учетом нелинейной работы. Далее можно выполнить
поверочный расчет нормального сечения плиты, как опорного, так и пролетного по
прочности и трещиностойкости на действие полученных усилий».

17.

Плоские безбалочные железобетонные перекрытия.
Правила проектирования.
/ Методическое пособие. Москва: ФАУ ФЦС, 2017./
Линейный расчет:
М надколонный / М пролетный = 6,3
Нелинейный расчет:
М надколонный / М пролетный = 6,2

18.

Статически неопределимые железобетонные конструкции.
/ Дыховичный А. А., Киев: Будiвельник, 1978./
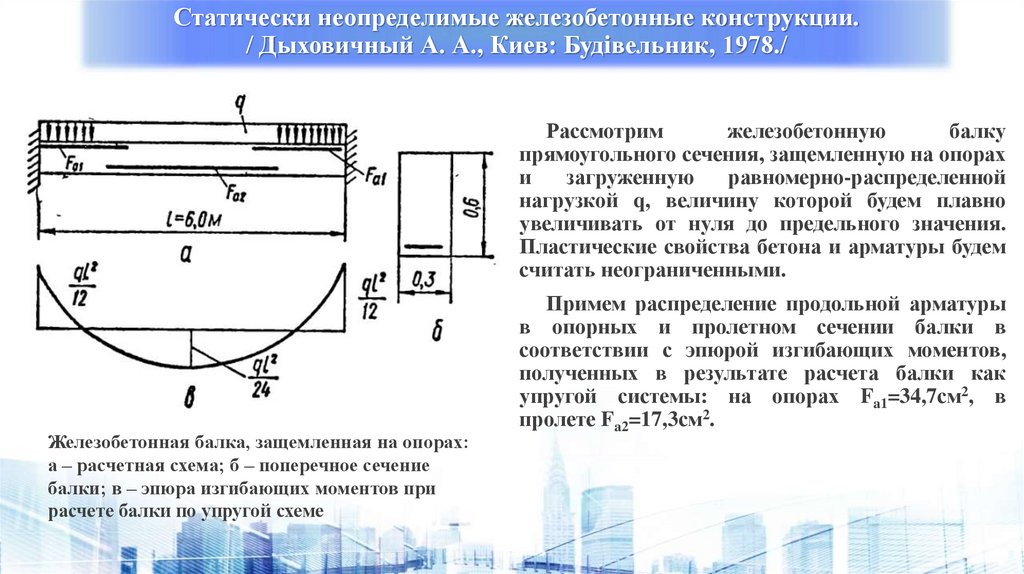
Рассмотрим
железобетонную
балку
прямоугольного сечения, защемленную на опорах
и
загруженную
равномерно-распределенной
нагрузкой q, величину которой будем плавно
увеличивать от нуля до предельного значения.
Пластические свойства бетона и арматуры будем
считать неограниченными.
Железобетонная балка, защемленная на опорах:
а – расчетная схема; б – поперечное сечение
балки; в – эпюра изгибающих моментов при
расчете балки по упругой схеме
Примем распределение продольной арматуры
в опорных и пролетном сечении балки в
соответствии с эпюрой изгибающих моментов,
полученных в результате расчета балки как
упругой системы: на опорах Fa1=34,7см2, в
пролете Fa2=17,3см2.

19.

Статически неопределимые железобетонные конструкции.
/ Дыховичный А. А., Киев: Будiвельник, 1978./
Разрушение балки начинается при нагрузке q= 17,0 т/м образованием пластических
шарниров в опорных сечениях. Вслед за этим, практически по той же величине внешней
нагрузки, образуется пластический шарнир в середине пролета, превращающий балку в
механизм.
Если при конструировании балки отступить от принятого распределения материала,
соответствующего расчету по упругой схеме, и общее количество арматуры разместить
поровну между опорными и пролетными сечениями, поведение балки в процессе не
изменится. Такое армирование (Fa1= Fa2= 26,0 см2) соответствует рекомендациям по
расчету статически неопределимых железобетонных конструкций с учетом
пластических деформаций, согласно которым Моп= Мпр= ql2/16. В этом случае
разрушение балки происходит при нагрузке q= 17,0 т/м от образования последнего
пластического шарнира в середине пролета.
Таким образом, хотя принятая схема армирования и отличалась от варианта,
рассмотренного первым, несущая способность балки не изменилась. Изменение схемы
армирования сказалось лишь на прогибах балки и соотношении опорных и пролетных
моментов.

20.

Статически неопределимые железобетонные конструкции.
/ Дыховичный А. А., Киев: Будiвельник, 1978./
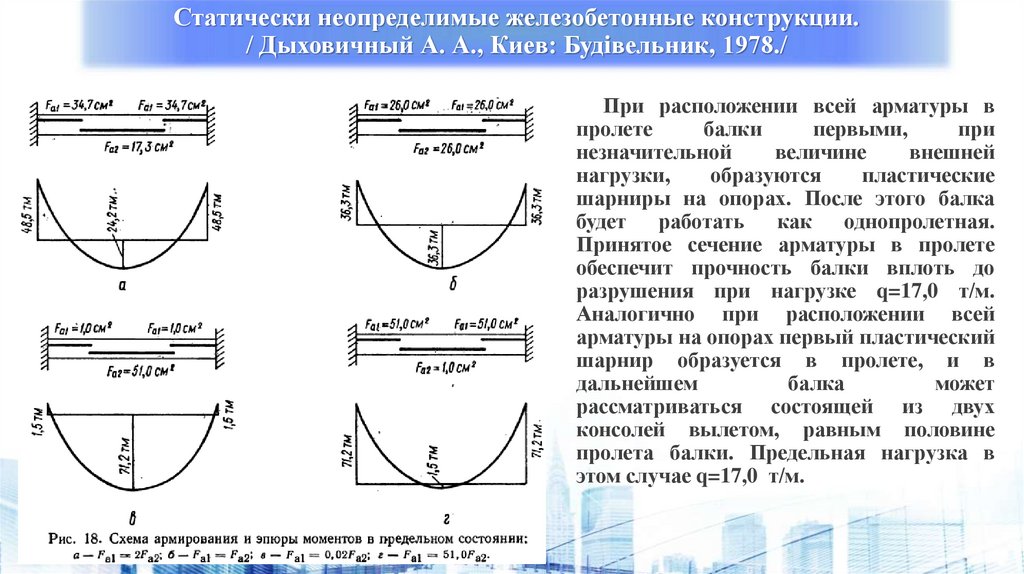
При расположении всей арматуры в
пролете
балки
первыми,
при
незначительной
величине
внешней
нагрузки,
образуются
пластические
шарниры на опорах. После этого балка
будет работать
как однопролетная.
Принятое сечение арматуры в пролете
обеспечит прочность балки вплоть до
разрушения при нагрузке q=17,0 т/м.
Аналогично при расположении всей
арматуры на опорах первый пластический
шарнир образуется в пролете, и в
дальнейшем
балка
может
рассматриваться состоящей из двух
консолей вылетом, равным половине
пролета балки. Предельная нагрузка в
этом случае q=17,0 т/м.

21.

Статически неопределимые железобетонные конструкции.
/ Дыховичный А. А., Киев: Будiвельник, 1978./
Последние варианты армирования нереальны. Теоретически вычисленная
несущая способность этих конструкций не отличается от несущей способности балок,
армированных по первым двум схемам. Но необходимо иметь ввиду, что пластические
деформации бетона и арматуры предполагались неограниченными, что не
соответствует реальным свойствам материалов. Очевидно, что деформации
отдельных волокон неармированных сечений достигнут предельных значений до того,
как образуется пластический шарнир в армированном сечении. Кроме того,
повышенная деформативность таких конструкций и значительная ширина
раскрытия трещин в слабо армированных сечениях потребуют ограничения
предельной нагрузки на основании расчета по второму предельному состоянию.

22.

СП 430.1325800.2018
Монолитные конструктивные системы.
Правила проектирования.
Метод заменяющих рам.
6.4.12
Расчет
регулярной
конструктивной
системы
методом
заменяющих
(эквивалентных) рам производят путем выделения отдельных рам вертикальными
сечениями, проходящими по середине шага колонн, в двух взаимно перпендикулярных
направлениях.
• Расчет выделенных в каждом направлении рам, состоящих из колонн и полос плоской
плиты (условного ригеля) следует производить независимо друг от друга по общим
правилам строительной механики на действие вертикальных и горизонтальных
нагрузок, принимая при определении усилий линейные жесткости элементов рам.
• Изгибающие моменты и поперечные силы в опорных и пролетных сечениях условного
ригеля распределяют между его надколонными и межколонными полосами в
зависимости от расположения колонн в раме (крайняя или промежуточная колонна) и
соотношения между поперечными и продольными (вдоль оси рамы) пролетами.

23.

СП 356.1325800.2017
КОНСТРУКЦИИ КАРКАСНЫЕ ЖЕЛЕЗОБЕТОННЫЕ МНОГОЭТАЖНЫХ ЗДАНИЙ.
Правила проектирования
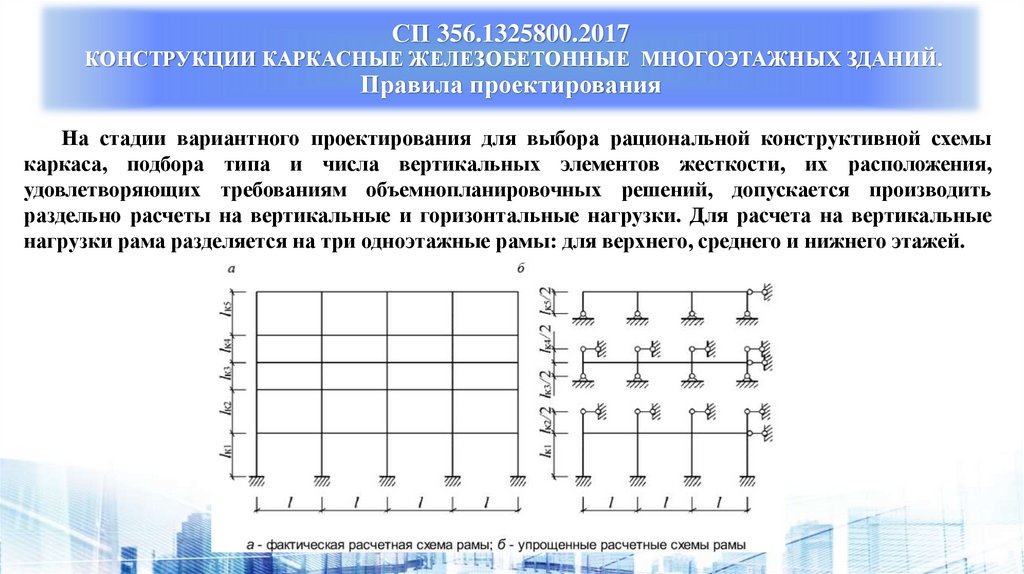
На стадии вариантного проектирования для выбора рациональной конструктивной схемы
каркаса, подбора типа и числа вертикальных элементов жесткости, их расположения,
удовлетворяющих требованиям объемнопланировочных решений, допускается производить
раздельно расчеты на вертикальные и горизонтальные нагрузки. Для расчета на вертикальные
нагрузки рама разделяется на три одноэтажные рамы: для верхнего, среднего и нижнего этажей.

24.

Плоские безбалочные железобетонные перекрытия.
Правила проектирования.
/ Методическое пособие. Москва: ФАУ ФЦС, 2017./
Данный метод расчета может быть
использован
при
проектировании
железобетонных каркасов зданий, состоящих
из колонн и жестко соединенных с ними плит
перекрытий, при ортогональной и регулярной
сетке колонн.
Рисунок 2.1 – Разделение каркаса на
заменяющие рамы:
1 – граница условного ригеля;
2 – условный ригель
Пространственная
конструкция
перекрытия
с
колоннами
разделяется
вертикальными плоскостями в двух взаимно
перпендикулярных направлениях на условные
рамы, которые включают колонны и
условный ригель. Ригель заменяющей рамы,
образуемый перекрытием, имеет ширину,
равную
расстоянию
между
серединами
соседних пролетов (рисунок 2.1). В общем
случае данный метод применяется для расчета
ребристых перекрытий, включающих балки.

25.

Плоские безбалочные железобетонные перекрытия.
Правила проектирования.
/ Методическое пособие. Москва: ФАУ ФЦС, 2017./
Расчет условного ригеля по нормальных сечениям на
действие изгибающего момента выполняют по общим
правилам
расчета
железобетонных
конструкций
в
соответствии с СП 63.13330.2012.
При расчете условный ригель разделяют на независимые
участки – надколонную и пролетную полосы (рисунок 2.2).
Коэффициенты распределения
условном ригеле:
Рисунок 2.2 – Разделение
условных ригелей на полосы:
1 – надколонная полоса;
2 – пролетная полоса.
изгибающих
моментов
в

26.

Руководство по расчету статически неопределимых
железобетонных конструкций.
/Москва: НИИЖБ, 1975./
4.9. Расчет на излом отдельной поперечной или продольной полосы панелей является
основным и во всех случаях обязательным. Он производится в предположении, что в
рассматриваемой полосе панелей образуются линейные пластические шарниры,
параллельные оси этой полосы:
один линейный пластический
шарнир в пролете с раскрытием
трещин снизу и по одному
линейному
пластическому
шарниру у опор с раскрытием
трещин сверху.

27.

Руководство по расчету статически неопределимых
железобетонных конструкций.
/Москва: НИИЖБ, 1975./

28.

Руководство по расчету статически неопределимых
железобетонных конструкций.
/Москва: НИИЖБ, 1975./

29.

Руководство по расчету статически неопределимых
железобетонных конструкций.
/Москва: НИИЖБ, 1975./

30.

Проектирование безбалочных бескапительных перекрытий.
/Дорфман А. Э., Левонтин Л. Н., Москва: Стройиздат, 1975./

31.

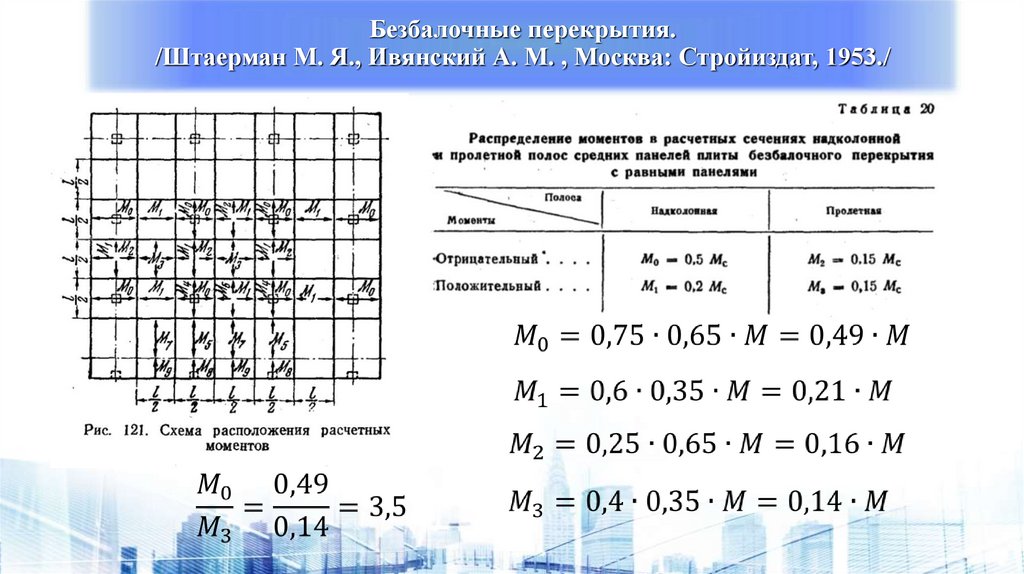
Безбалочные перекрытия.
/Штаерман М. Я., Ивянский А. М. , Москва: Стройиздат, 1953./

32.

Безбалочные перекрытия.
/Штаерман М. Я., Ивянский А. М. , Москва: Стройиздат, 1953./

33.

Жилой комплекс «Атлант- Сити», г. Нижний Новгород.
Общий вид здания.

34.

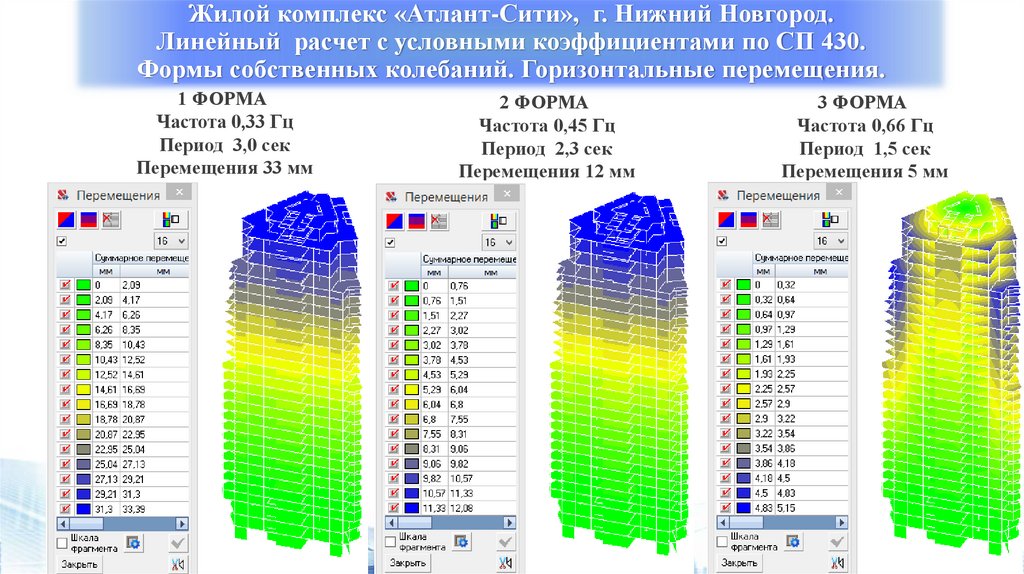
Жилой комплекс «Атлант-Сити», г. Нижний Новгород.
Линейный расчет с условными коэффициентами по СП 430.
Формы собственных колебаний. Горизонтальные перемещения.
1 ФОРМА
Частота 0,33 Гц
Период 3,0 сек
Перемещения 33 мм
2 ФОРМА
Частота 0,45 Гц
Период 2,3 сек
Перемещения 12 мм
3 ФОРМА
Частота 0,66 Гц
Период 1,5 сек
Перемещения 5 мм

35.

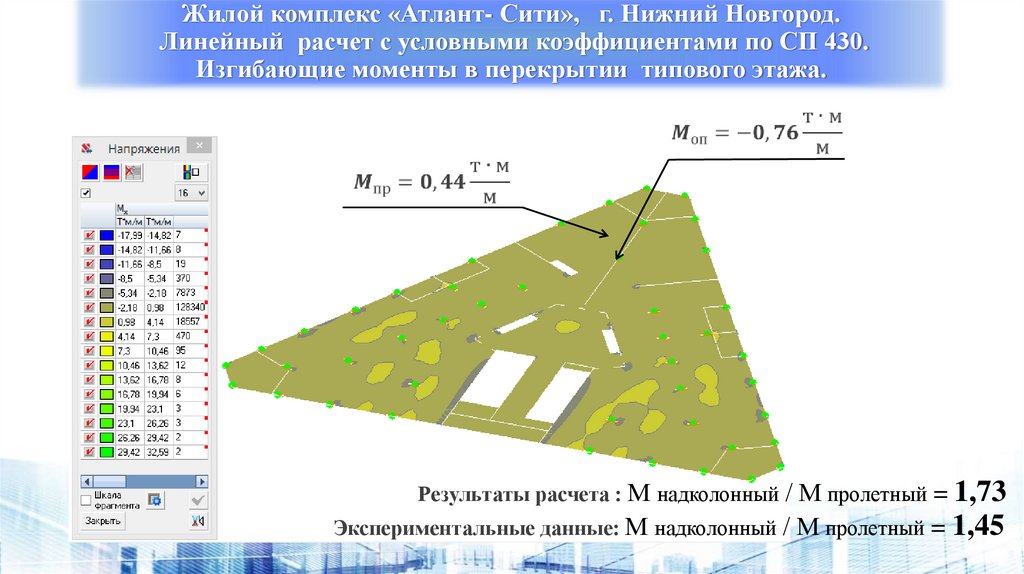
Жилой комплекс «Атлант- Сити», г. Нижний Новгород.
Линейный расчет с условными коэффициентами по СП 430.
Изгибающие моменты в перекрытии типового этажа.
Результаты расчета : М надколонный / М пролетный = 1,73
Экспериментальные данные: М надколонный / М пролетный = 1,45

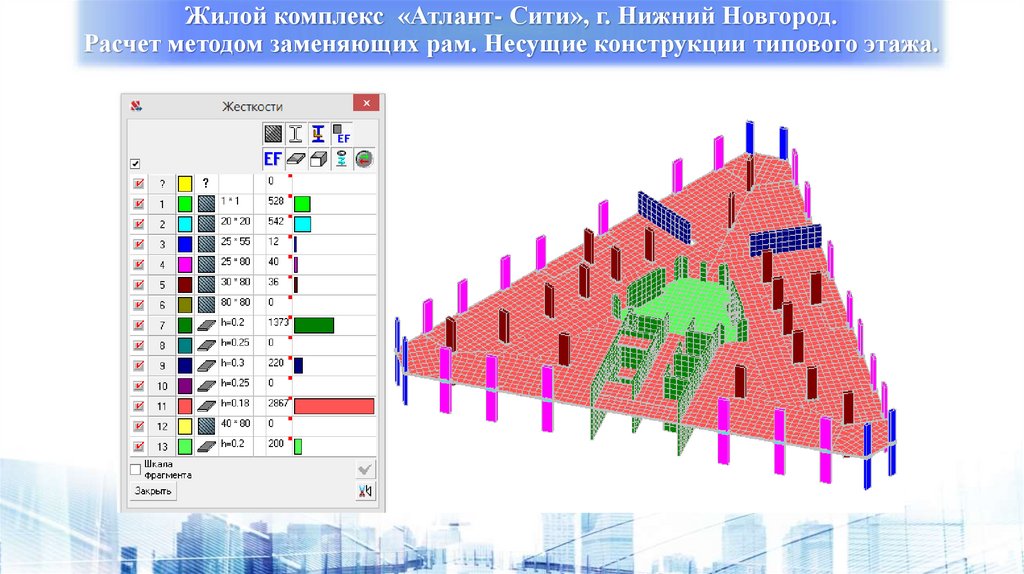
36.

Жилой комплекс «Атлант- Сити», г. Нижний Новгород.
Расчет методом заменяющих рам. Несущие конструкции типового этажа.

37.

Жилой комплекс «Атлант- Сити», г. Нижний Новгород.
Расчет методом заменяющих рам. Приведенная рама типового этажа.

38.

Жилой комплекс «Атлант- Сити», Нижний Новгород.
Расчет методом заменяющих рам. Перераспределение арматуры.
Средний пролет:
• Площадь пролетной арматуры по линейному расчету – 5,62 см2
• Площадь опорной арматуры слева и справа по линейному расчету - 7,02 см2
• Принятое армирование опорного и пролетного сечения : 0,5 х F = 12,64 х 0,5 = 6,32 см2
Крайний пролет:
• Площадь пролетной арматуры по линейному расчету - 6,11 см2
• Площадь опорной арматуры по линейному расчету - 6,11 см2 (слева) и 9,56 см2 (справа)
• Принятое армирование:
• в пролете: 0,5 х F = 13,95 х 0,5 = 6,97 см2
• на опоре слева : 0,5 х 0,33 х F = 0,5 х 0,33 х 13,95 = 2,3 см2
• на опоре справа : 0,5 х 0,67 х F = 0,5 х 0,67 х 16,52 = 4,6 см2

39.

Жилой комплекс «Атлант-Сити». г. Нижний Новгород.
Расчет методом заменяющих рам. Результаты расчета.
Линейный расчет
Нелинейный расчет с перераспределенной арматурой

40.

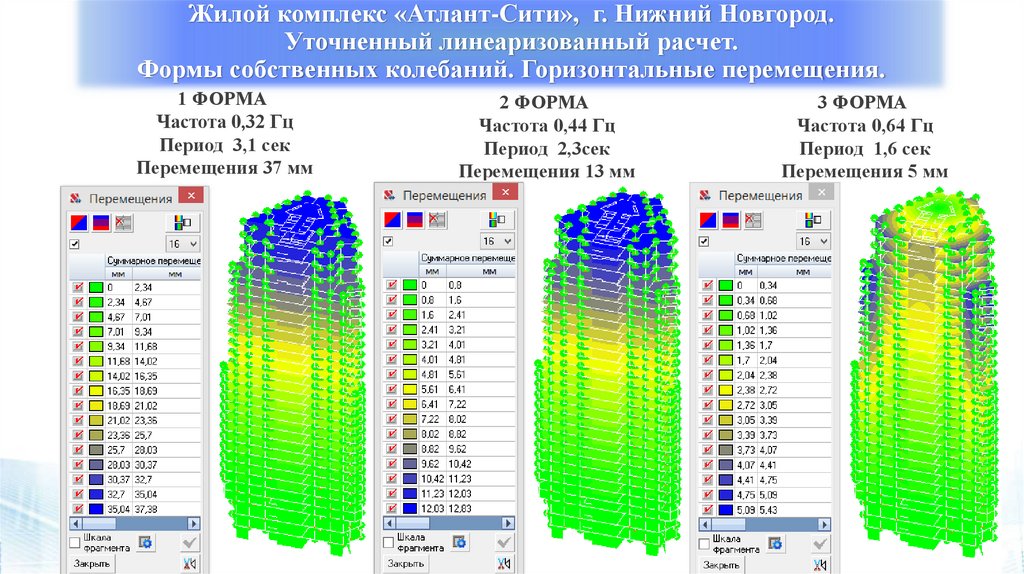
Жилой комплекс «Атлант-Сити», г. Нижний Новгород.
Уточненный линеаризованный расчет.
Формы собственных колебаний. Горизонтальные перемещения.
1 ФОРМА
Частота 0,32 Гц
Период 3,1 сек
Перемещения 37 мм
2 ФОРМА
Частота 0,44 Гц
Период 2,3сек
Перемещения 13 мм
3 ФОРМА
Частота 0,64 Гц
Период 1,6 сек
Перемещения 5 мм

41.

Жилой комплекс «Атлант- Сити», г. Нижний Новгород.
Уточненный линеаризованный расчет.
Изгибающие моменты в перекрытии типового этажа.
Результаты расчета : М надколонный / М пролетный = 1,48
Экспериментальные данные: М надколонный / М пролетный = 1,45

42.

Общие выводы.
1.
2.
3.
4.
5.
Расчет монолитных конструктивных систем с использованием нелинейного процессора
(физической нелинейности) в среде SCAD Office дает качественную сходимость с реальной
работой несущих железобетонных конструкций и экспериментальными данными.
Последовательное использование линейного и нелинейного процессора (рекомендуемое
методическими пособиями), без выполнения многочисленных уточняющих армирование
поверочных расчетов ( по прочности и
трещиностойкости) не позволяет получить
оптимальное конструирование железобетонных элементов.
Использование
метода
заменяющих
рам
позволяет
выполнить
требования
СП 430.1325800.2018, значительно ускорить работу с нелинейным процессором (физической
нелинейностью) в среде SCAD Office для расчета монолитных конструктивных систем и
получить оптимальное армирование несущих конструкций.
Для выполнения требований СП 63.13330.2018 «Бетонные и железобетонные конструкции» и
СП 20.13330.2016 «Нагрузки и воздействия» к проектированию монолитных конструктивных
систем необходимо применять линейный расчет с линеаризованными (условными)
жесткостями, определяемыми по результатам расчета, с использованием нелинейного
процессора (физической нелинейности) в среде SCAD Office.
Выполнение уточненных лениаризированных расчетов для отдельных конструктивных
элементов ( верхнего, нижнего и средних этажей) может осуществляться
без внесения
изменений в общую пространственную схему здания.

43. Расчет конструкций монолитных железобетонных многоэтажных зданий по СП 430.1325800.2018

ГАУ НО «Управление государственной
экспертизы проектной документации по Нижегородской области»
Официальный сайт: www.ugenn.ru
Электронная почта: [email protected]
ООО МСК «Мост-К»
Официальный сайт: www.most-k.ru
Электронная почта: [email protected]
Благодарим за внимание!
Московский международный семинар
«Расчет и проектирование конструкций в среде SCAD Office 21»
г. Москва, 21 апреля 2020 г.